ACT Math 1 - Formulas and Definitions

Commutative Property

Order of operands can be changed without affecting the result in addition and multiplication operations.

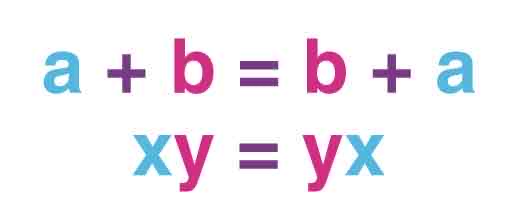
Associative Property

The grouping of operands doesn't change the result in addition and multiplication operations.

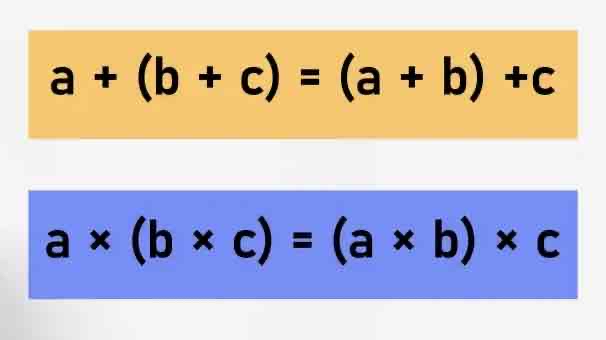
Distributive Property

Multiplying a number by a sum (or difference) is the same as multiplying the number by each term in the sum (or difference)

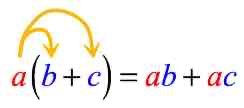
Identity Property

The sum of any number and zero is the number itself, and the product of any number and one is the number itself.

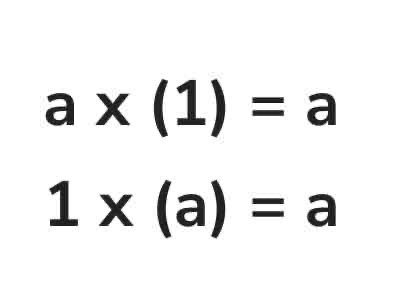
Inverse Property

For any number, there exists an additive inverse such that when added together, they result in zero, and a multiplicative inverse such that when multiplied together, they result in one.

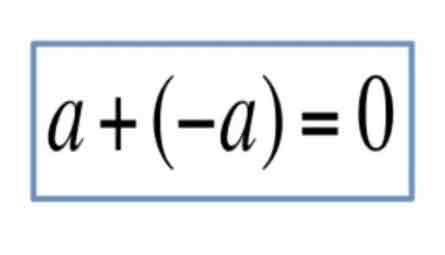
Translation

(x, y) → (x+a, y+a)

Reflection across the x-axis

(x, y) → (x, -y)

Reflection across the y-axis

(x, y) → (-x, y)

Reflection across the line y=x

(x, y) → (y, x)

Rotation 90 about the origin

(x, y) → (-y, x)

Rotation 180 about the origin

(x, y) → (-x, -y)

Rotation 270 about the origin

(x, y) → (y, -x)

Dilation with respect to the origin and scale factor of k

(x, y) → (kx, ky)

Conditional statement

If A, then B

Converse

If B, then A

Inverse

If not A, then not B

Contrapositive

If not B, then not A

Biconditional

A if and only if B

Reflexive Property

a = a

Symmetric Property

If a = b, then b = a

Transitive Property

If a = b, and b = c, then a = c

Simple Interest

I = Prt

Compound Interest

A = P(1+r)^t

Compound Interest (GF)

A= P(1+r/n)^nt