Maths - Algebra and Quadratics

Distributive Law

    a(b + c) = ab + ac

Expand a single bracket

    a(b ± c) = ab ± ac

Expand binomials: (a + b)(c + d)

    = ac + ad + bc + bd

Perfect square: (a + b)²

    = a² + 2ab + b²

Perfect square: (a - b)²

    = a² - 2ab + b²

Difference of squares: (a + b)(a - b)

 = a² - b²

Algebraic fraction – Common Denominator

 Make the denominators the same, then add/subtract the numerators.

Add/Subtract Algebraic Fractions

 1. Find common denominator
    2. Adjust numerators
    3. Add or subtract
    4. Simplify

TI-Nspire Command: Expand

Menu —> algebra —> expand

Command: Calculate

Give a numerical answer with clear steps.

Command: Find

Give an answer with working shown.

Command: Hence

Use your previous answer to solve the next part.

Command: Hence or Otherwise

Use your previous work, or solve it another way.

Command: Expand

Multiply out brackets to remove them.

Command: Simplify

Give your answer in its most reduced form.

What does "factorised form" mean?

An expression written as a product of its factors, not expanded. Example:
x² + 5x = x(x + 5)

First step in any factorising problem?

Always check for a common factor first.

Recognising a difference of perfect squares

Look for patterns like:
a² – b² = (a + b)(a – b)
Includes expressions like:
x² – 4, x² – √2, 9x² – 16y²

Factorising with a common factor

Take out the highest common factor (HCF) from each term.
Example: 6x + 12 = 6(x + 2)

Factorising difference of perfect squares

a² – b² = (a + b)(a – b)

Grouping technique (4 terms)

Group terms in pairs, then factor each group.
Example:
ax + ay + bx + by = a(x + y) + b(x + y) = (a + b)(x + y)

What is a monic quadratic trinomial?

A trinomial where the coefficient of x² is 1.
Example: x² + 5x + 6

Factorising a monic quadratic

Find two numbers that add to the middle term and multiply to the last term.
Example: x² + 5x + 6 = (x + 2)(x + 3)

Link between expanding and factorising

Expanding brackets builds a trinomial, factorising breaks it back down into brackets.

Simplifying algebraic fractions

1. Factor numerator and denominator

2. Cancel common factors

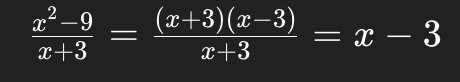
Factorising a non-monic quadratic

• Multiply a × c

• Find factors of that product that add to b

• Use grouping to factor
  Example:
  2x² + 7x + 3 = (2x + 1)(x + 3)

Expanded form of a perfect square

(a+b)² = a² + 2ab + b²

(a- b)² = a² - 2ab + b²

Completing the square (steps)

1. Half the middle term

2. Square it

3. Add and subtract inside the expression
   Example:
   x² + 6x → (x + 3)² – 9

Factorise by completing the square

• Complete the square

• Write it as a squared binomial
  Example:
  x² + 6x + 9 = (x + 3)²

Can all quadratics be factorised?

No – if there are no integer factors that work, it can’t be factorised using basic methods.

TI-Nspire: Factor command —> factor

Menu → 3: Algebra → 2: Factor

Null Factor Law

ab = 0, then a = 0 or b = 0

standard form

ax² + bx + c = 0

Solving a worded quadratic problem

1. Create an equation using the context

2. Rearrange into standard form

3. Solve using factoring, completing the square, or the formula

Solve using completing the square

• Write in form: (x + p)² = q

• Solve by square root method

Number of solutions to a quadratic

Use the discriminant:
Δ = b² – 4ac

• If Δ > 0 → 2 solutions

• If Δ = 0 → 1 solution

• If Δ < 0 → No real solution

discriminate

Δ = b² – 4ac

Quadratic Formula

x = (–b ± √(b² – 4ac)) / 2a

Key features of a parabola

• x-intercepts

• y-intercept

• Turning point (vertex)

• Axis of symmetry

• Direction (opens up/down)

Dilation or reflection in a parabola

y = a(x – h)² + k

• |a| > 1 = narrower

• |a| < 1 = wider

• a < 0 = reflection (opens down)

Translations of a parabola

• h = horizontal shift

• k = vertical shift

Find turning point using x-intercepts

Midpoint of x-intercepts = x-value of turning point
Sub into equation to find y

Perfect square parabola

y = (x ± a)²

• Only touches x-axis once

• Vertex is on the axis

turning point form

y = a(x – h)² + k

• Vertex: (h, k)

Sketching by completing the square

Convert to turning point form:
y = a(x – h)² + k, then sketch

Turning point using formula

x = –b / 2a, then sub into the equation to find y

Sketching using quadratic formula

Find x-intercepts using:
x = (–b ± √(b² – 4ac)) / 2a
Then plot vertex and shape

Solve quadratic inequalities

1. Solve like a normal quadratic

2. Use a number line to test intervals

3. Write in inequality form

Points of intersection: line and parabola

• Set equations equal

• Solve resulting quadratic

• Solutions are x-values of intersection

TI-Nspire: Solve equation

Menu → 3: Algebra → 1: Solve

TI-Nspire: Find x-intercepts (zeros)

Menu → 6: Analyse Graph → 1: Zero

TI-Nspire: Find turning point (min/max)

Menu → 6: Analyse Graph → 2: Minimum or 3: Maximum