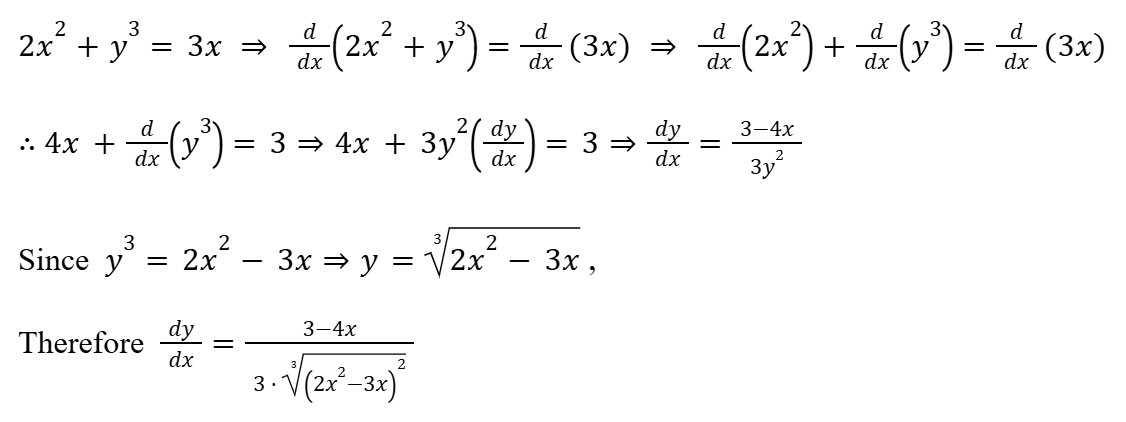UNIT 5.1. Differentiation

0.0(0)
learnLearn
examPractice Test
spaced repetitionSpaced Repetition
heart puzzleMatch
flashcardsFlashcards
Card Sorting

1/11

flashcard set

Earn XP

Description and Tags

Formulae (SL & HL)

IB Mathematics: Analysis and Approaches (HL)

Calculus

Study Analytics
Name
Mastery
Learn
Test
Matching
Spaced

No study sessions yet.

12 Terms

1
New cards

Limits

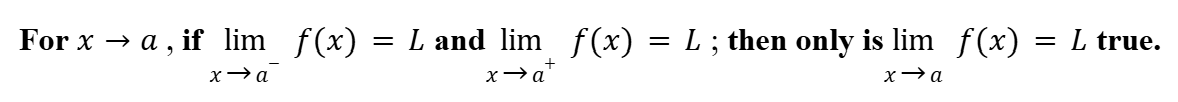
knowt flashcard image
2
New cards

Limit Formula

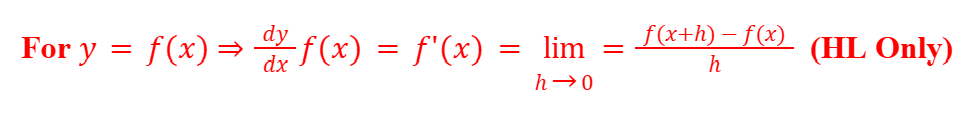
knowt flashcard image
3
New cards

Power Rule (Differentiation)

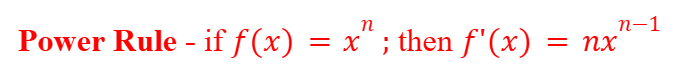
knowt flashcard image
4
New cards

Chain Rule (Differentiation)

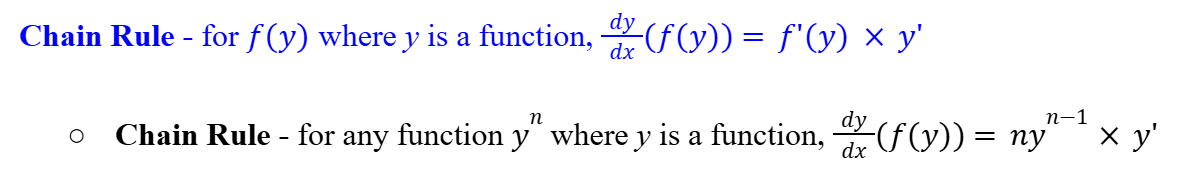
knowt flashcard image
5
New cards

Product Rule (Differentiation)

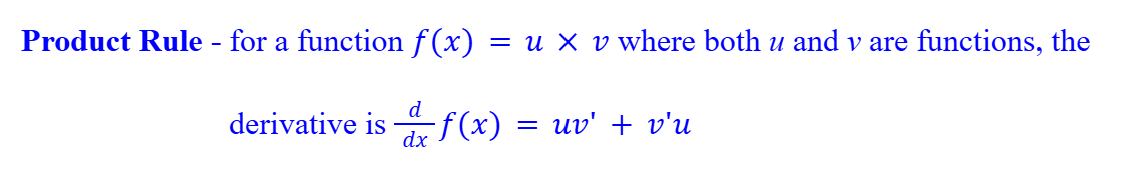
knowt flashcard image
6
New cards

Quotient Rule (Differentiation)

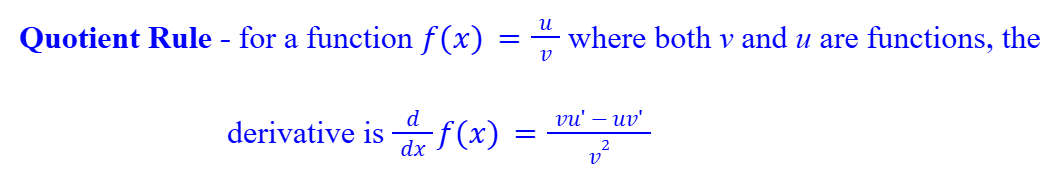
knowt flashcard image
7
New cards

Standard Derivatives of Functions

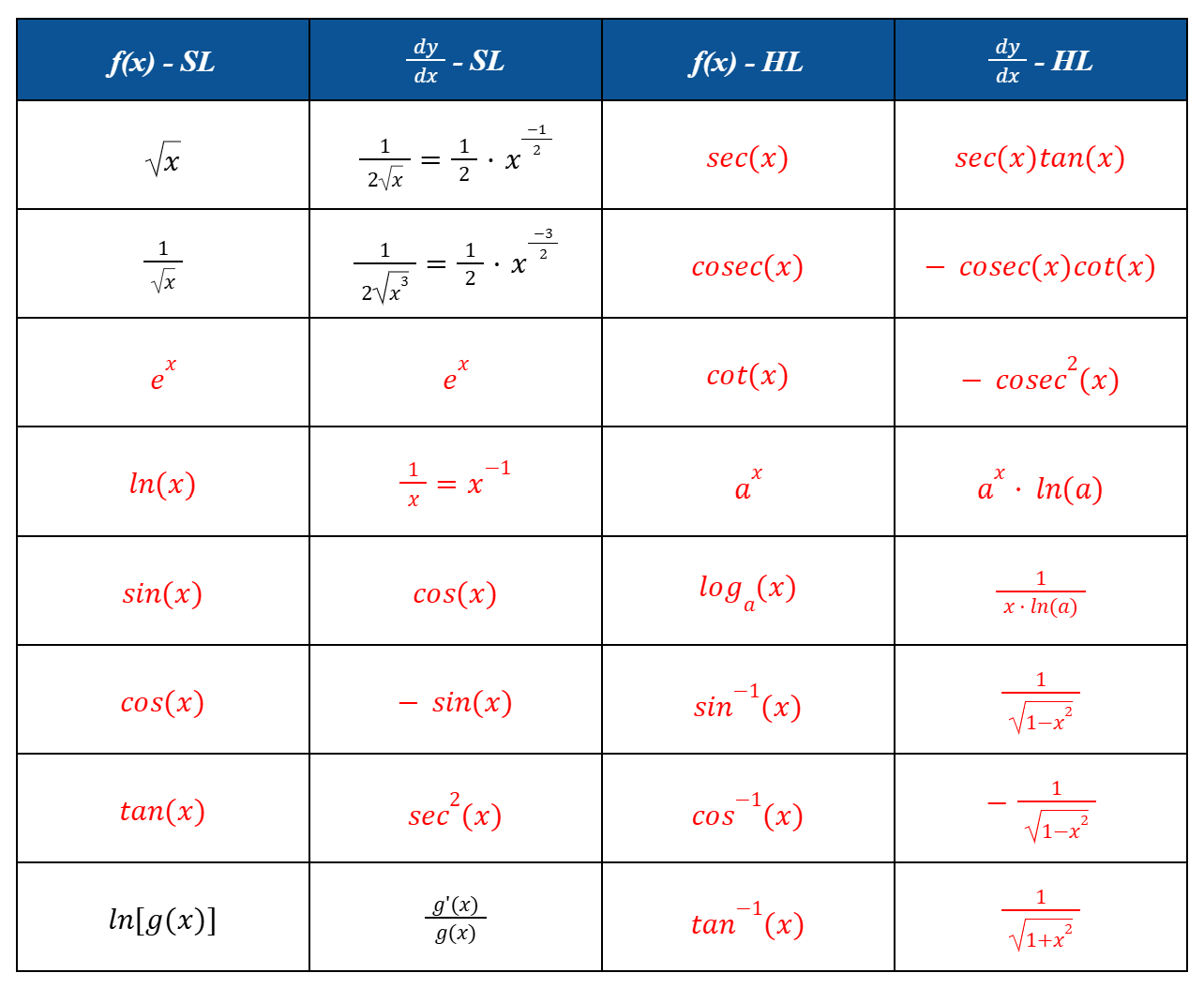
knowt flashcard image
8
New cards

Local Maximums (Differentiation)

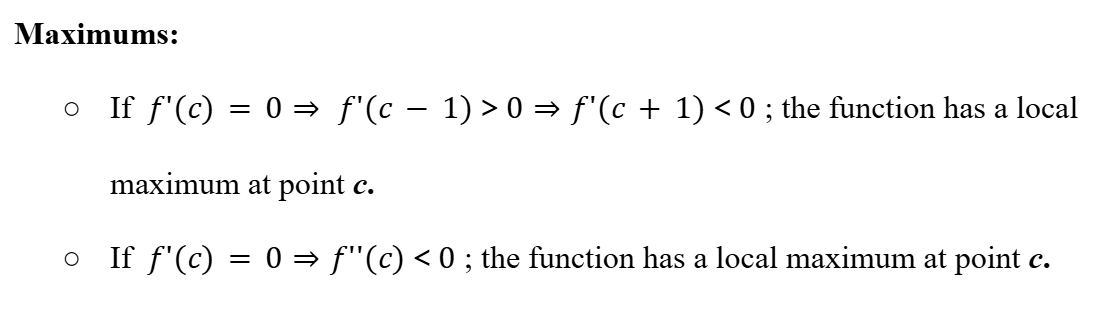
knowt flashcard image
9
New cards

Local Minimums (Differentiation)

knowt flashcard image
10
New cards

Continuity (Differentiation)

  • Continuity - A Function is continuous if:

    • f(x) is defined at every point in a domain.

    • There is a limit at every point.

    • The limit at a point is equal to the functional value at that point.

<ul><li><p><span><strong>Continuity - A Function is continuous if:</strong></span></p><ul><li><p><span>f(x) is defined at every point in a domain.</span></p></li><li><p><span>There is a limit at every point.</span></p></li><li><p><span>The limit at a point is equal to the functional value at that point.</span></p></li></ul></li></ul><p></p>
11
New cards

L’Hopital’s Rule

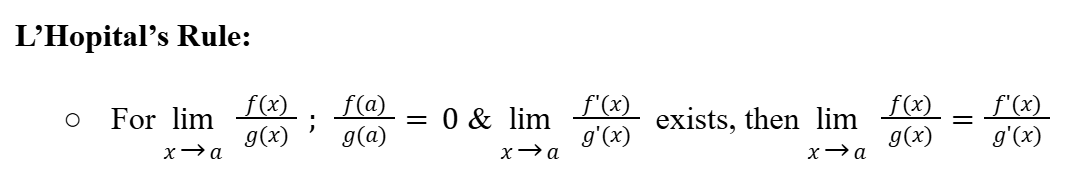
knowt flashcard image
12
New cards

Implicit Differentiation

For any function with more than one variable, consider the variable that is not differentiated with respect to a function.

<p><span>For any function with more than one variable, consider the variable that is not differentiated with respect to a function.</span></p>