The Matrix of a Linear Transformation 1.9

Any linear transformation can be written as..

A matrix equation

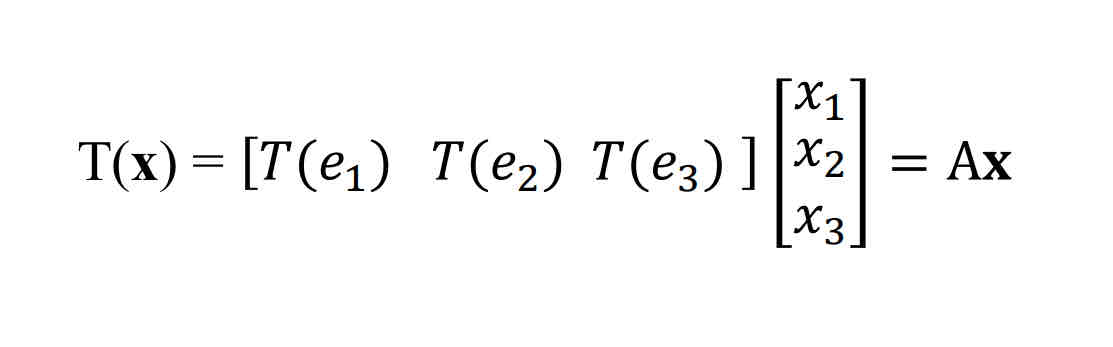
Theorem 10: Let T: R^n ➡R^m be a linear transformation. Then there exist…

A unique matrix A such that T(x) = Ax for all x in R^n

What is the difference between linear transformation and matrix transformation?

The term linear transformation focuses on a property of a mapping, while matrix transformation describes how such mapping is implemented

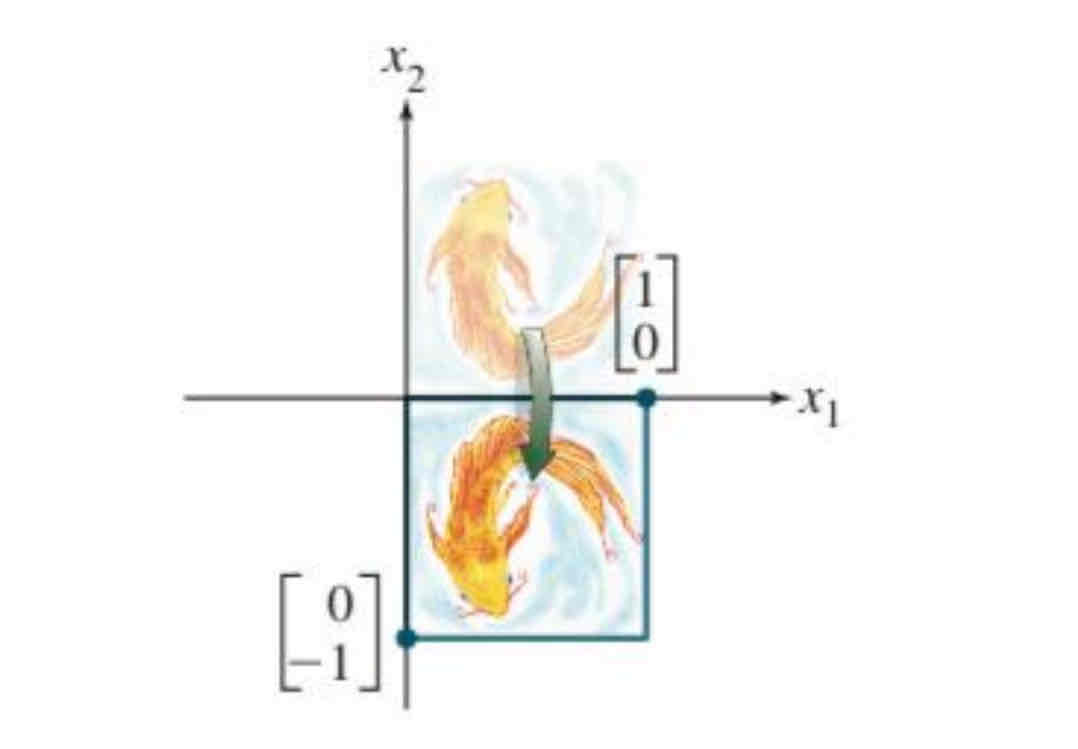
Reflection through the x1 axis

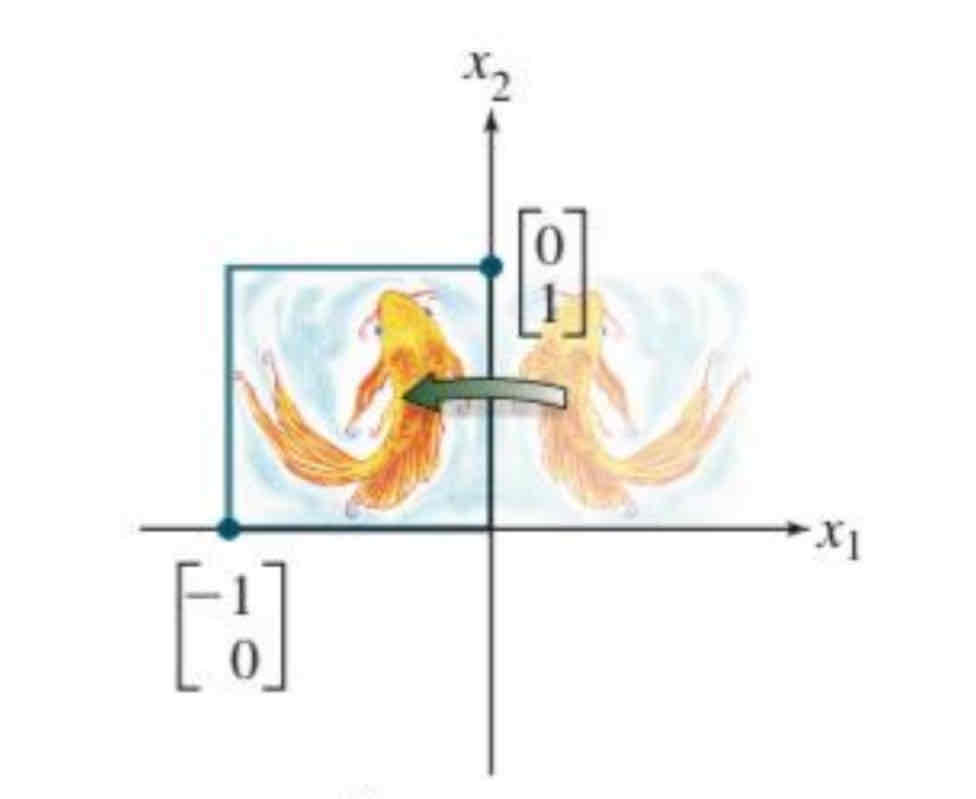
Reflection through the x2 axis

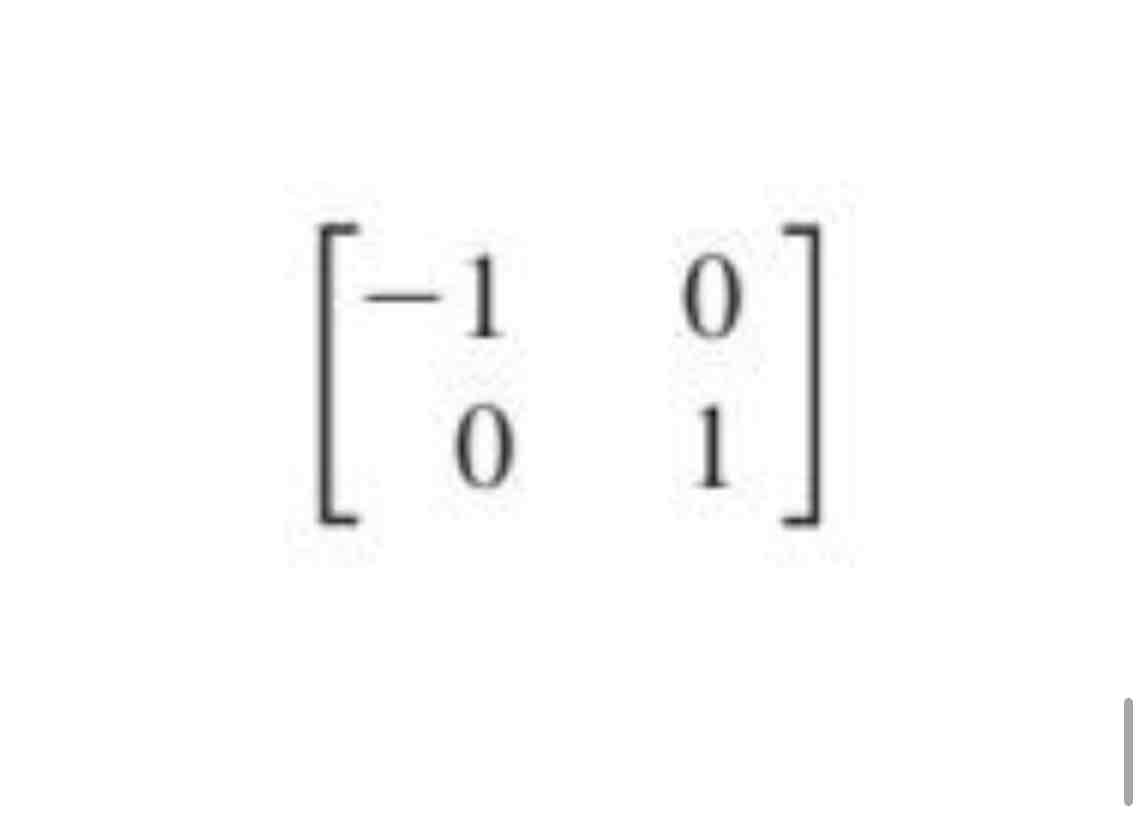
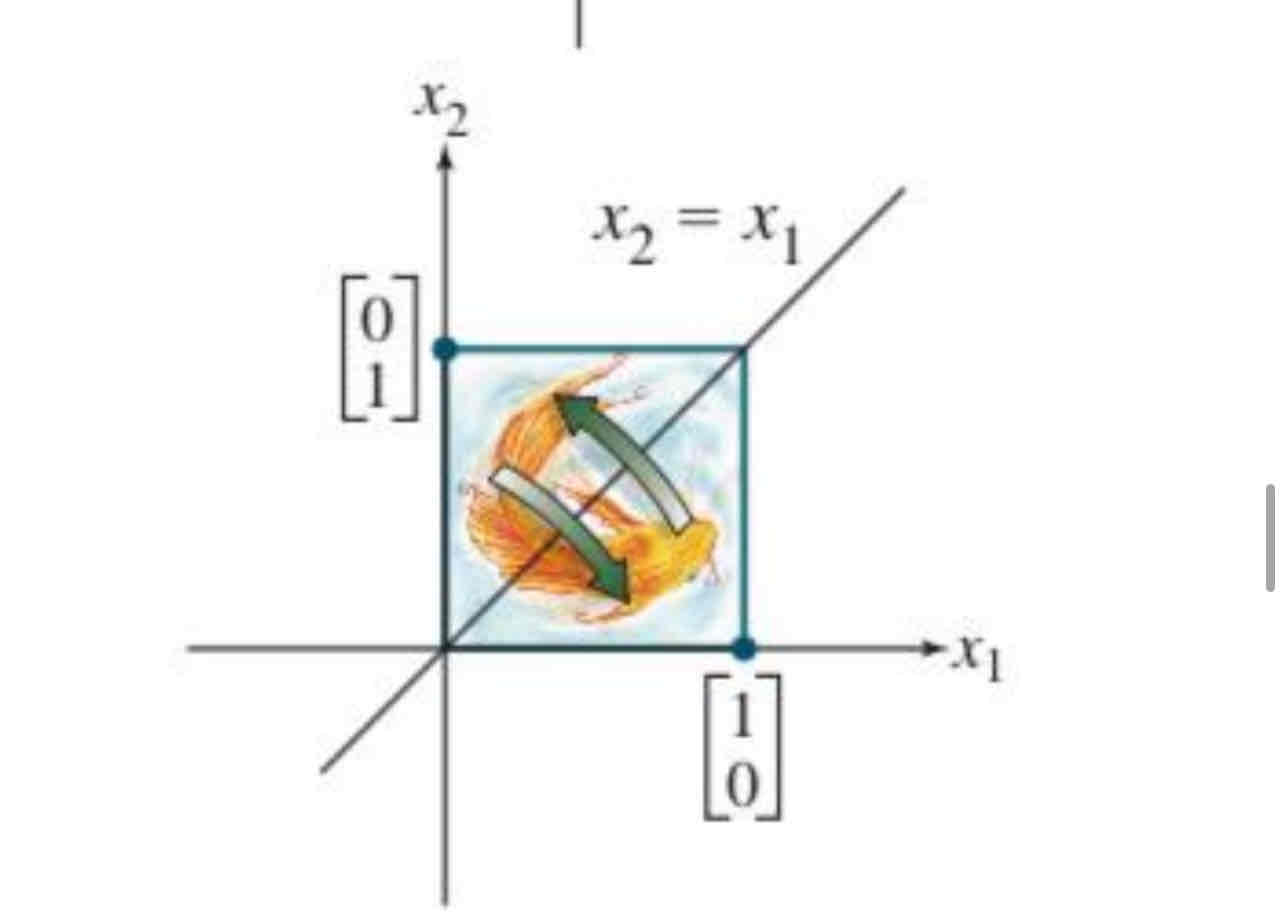
Reflection through the line x2 = x1

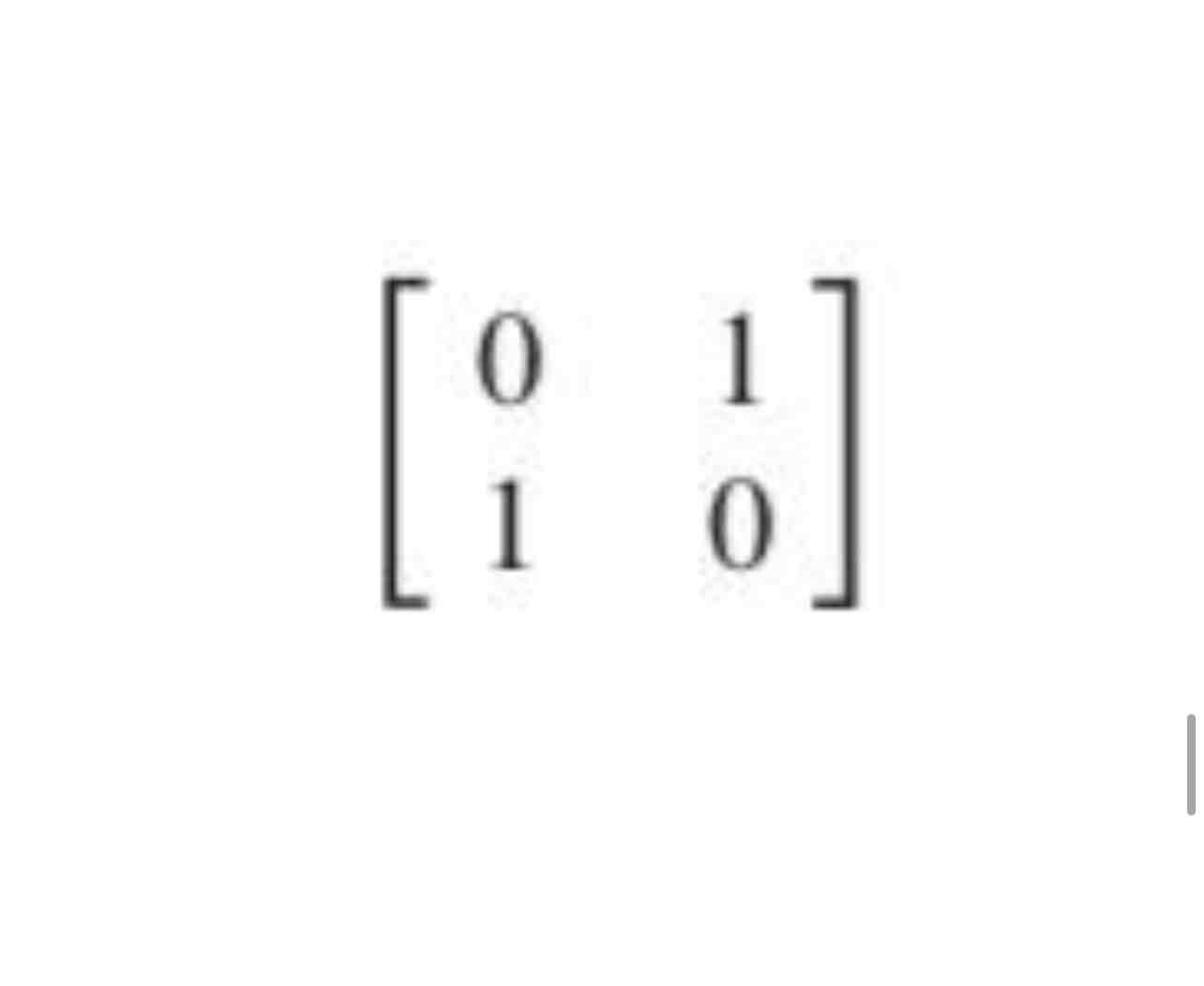
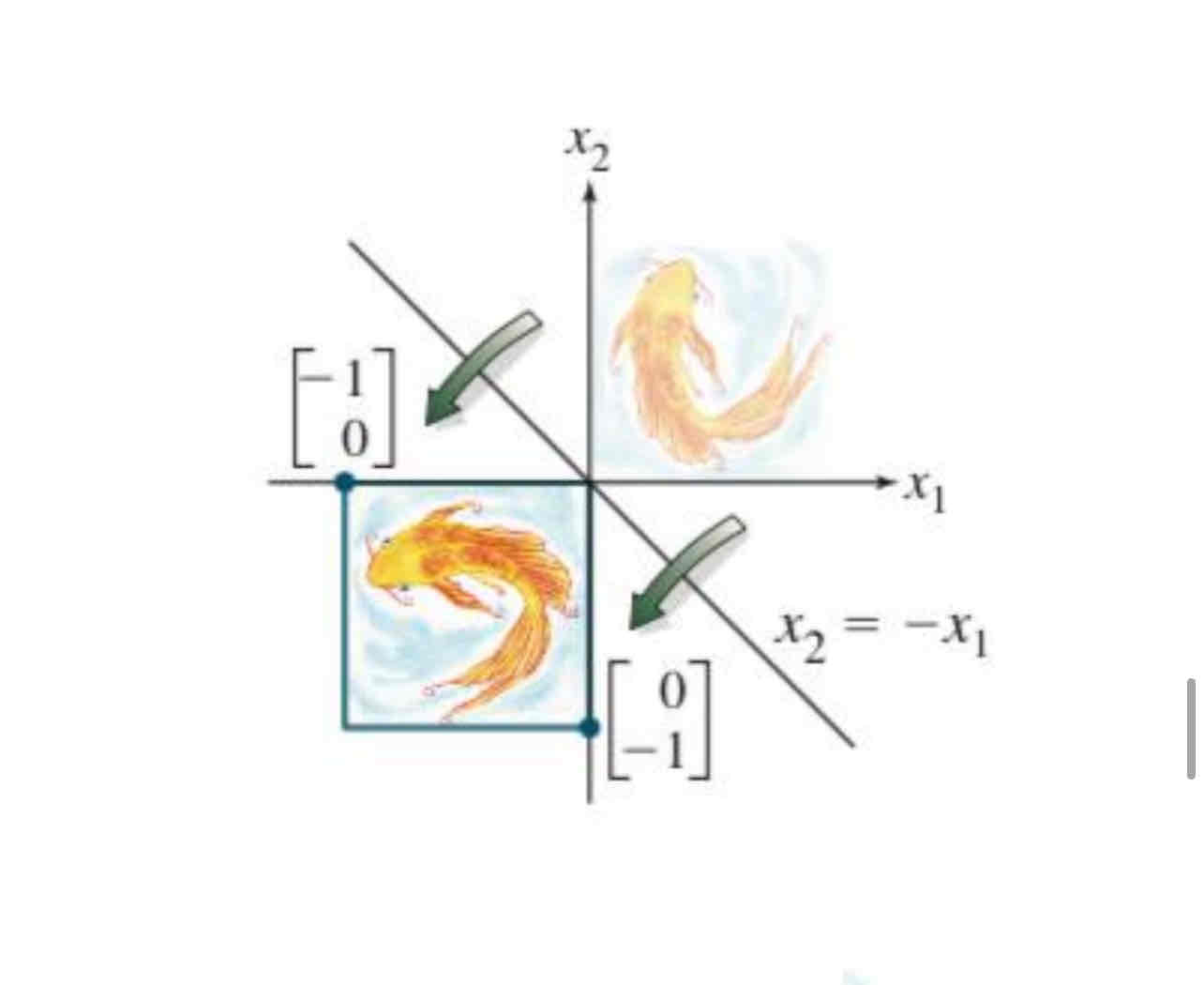
Reflection through the line x2 = -x1

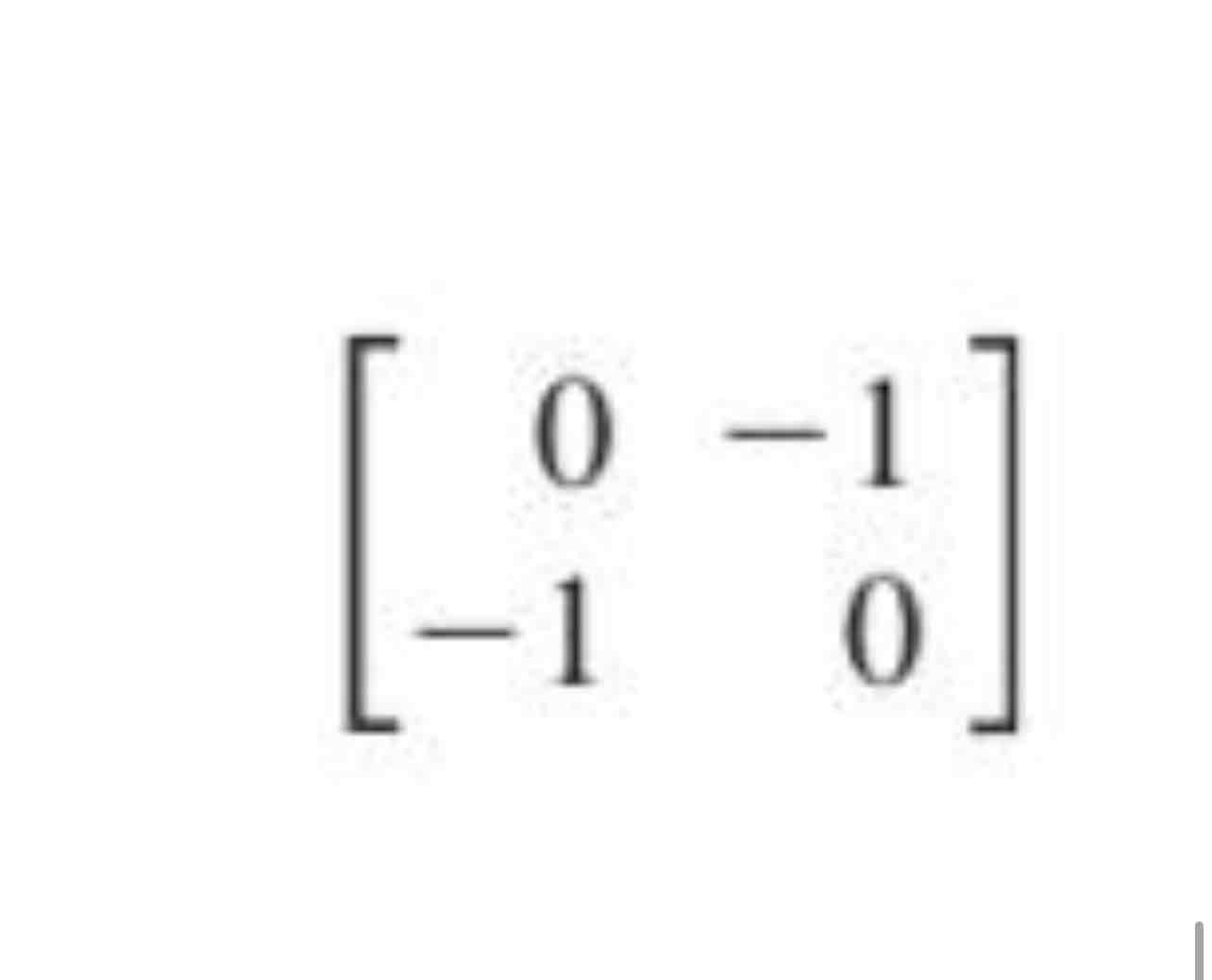
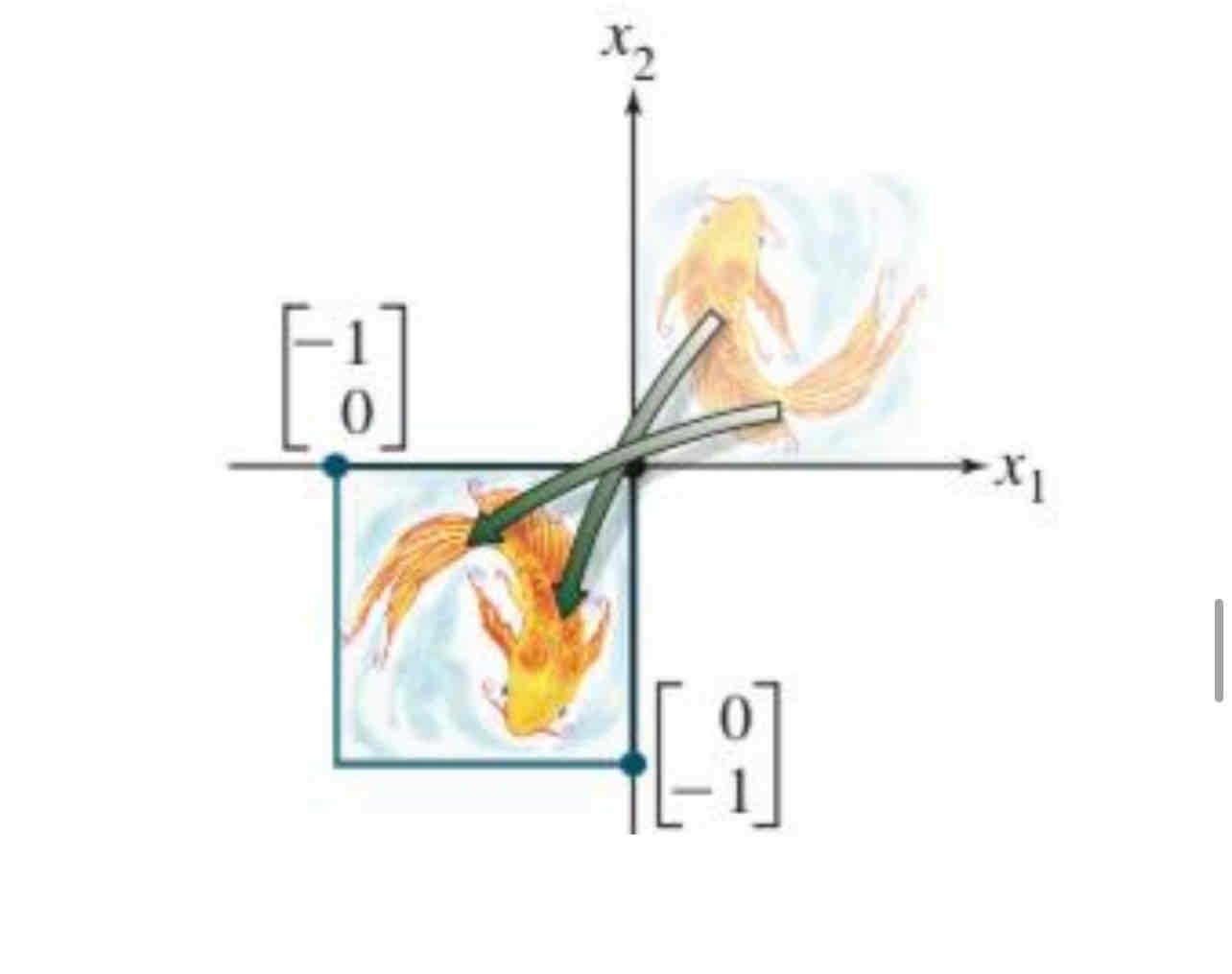
Reflection through the origin

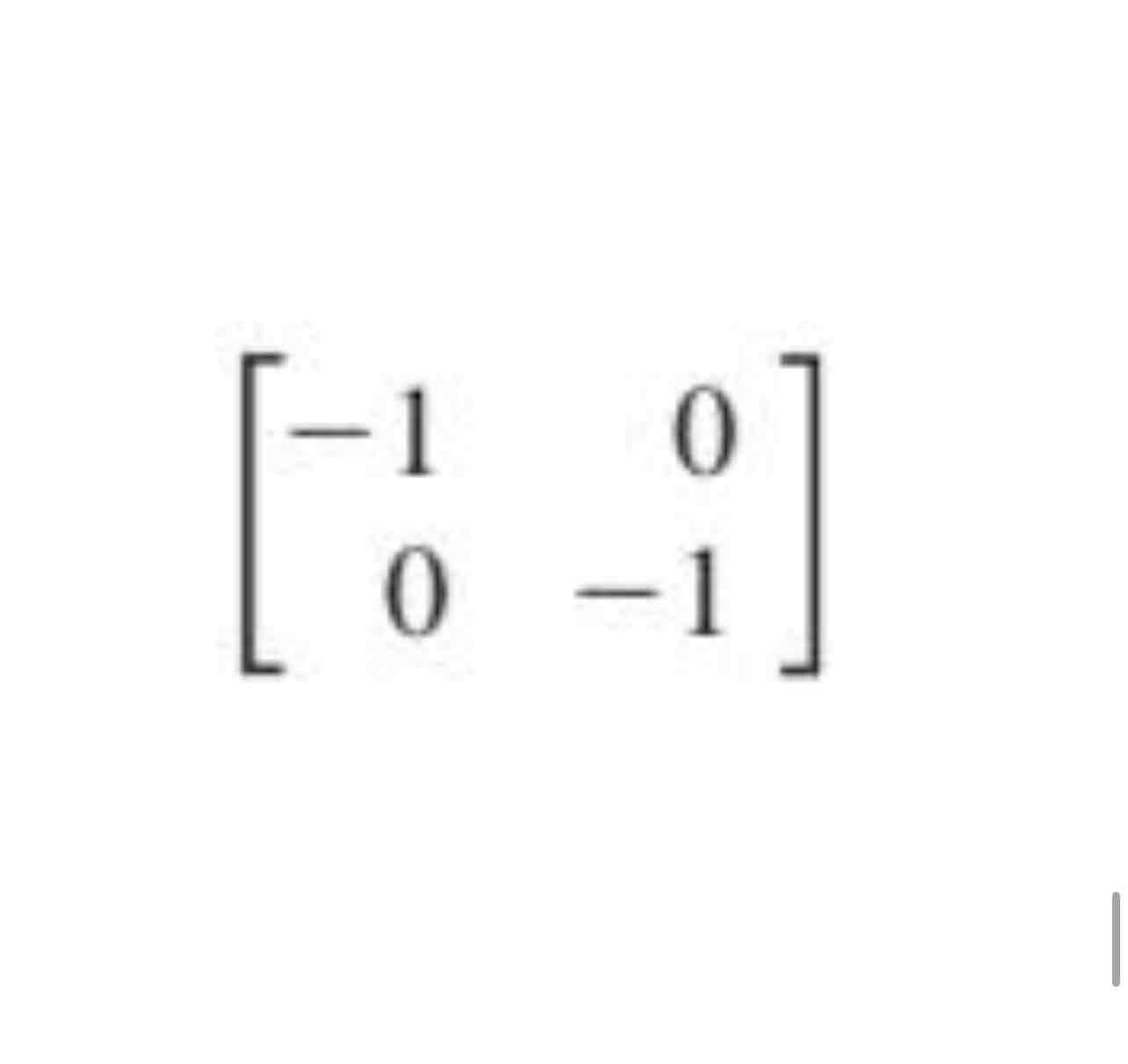
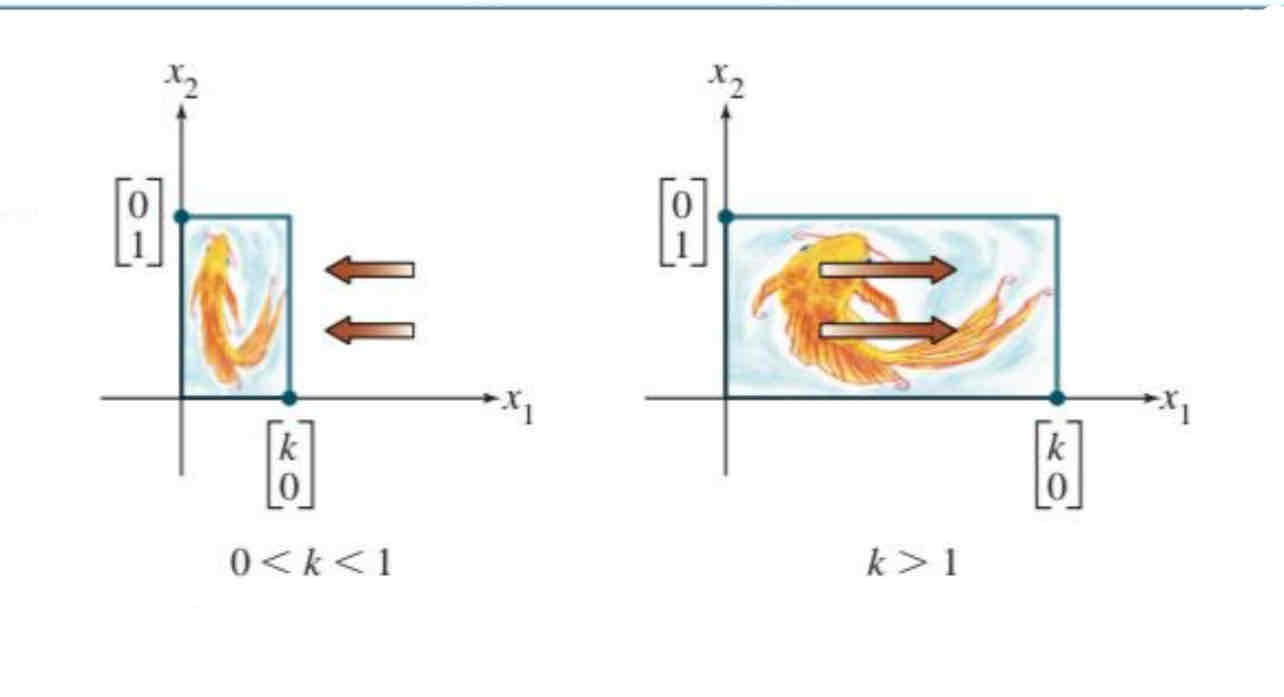
Horizontal contraction and expansion

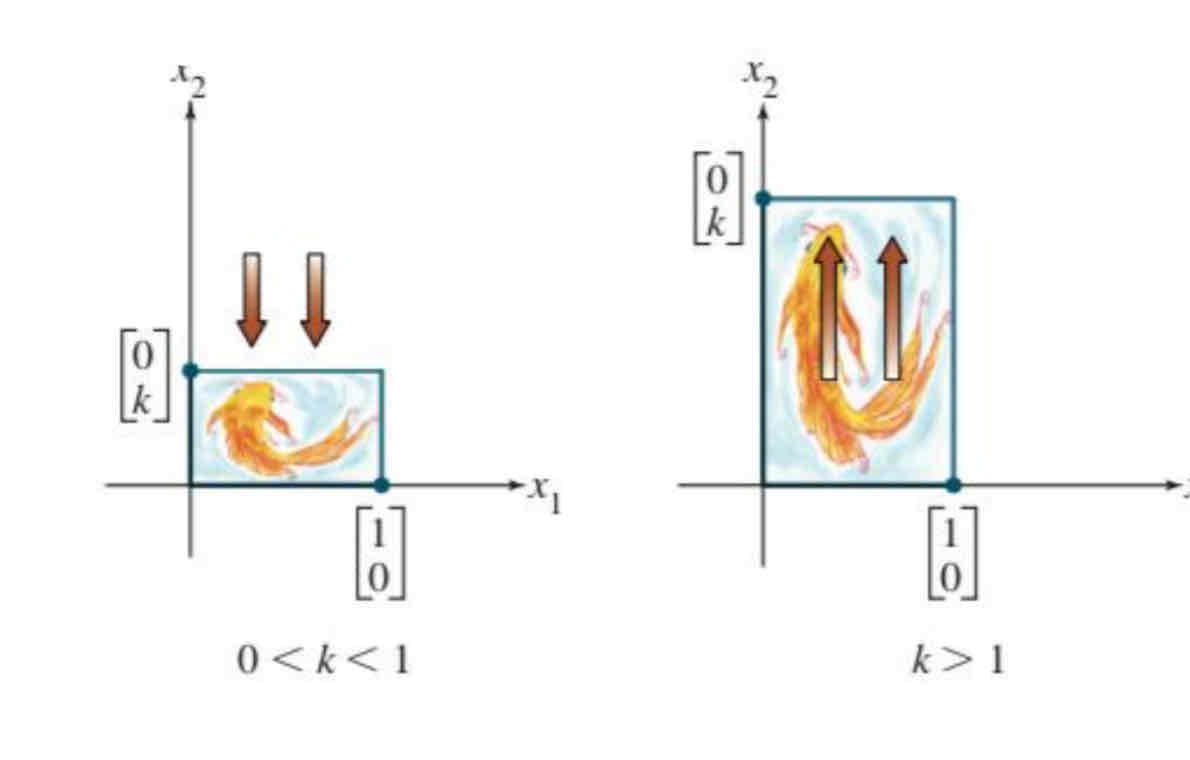
Vertical contraction and expansion

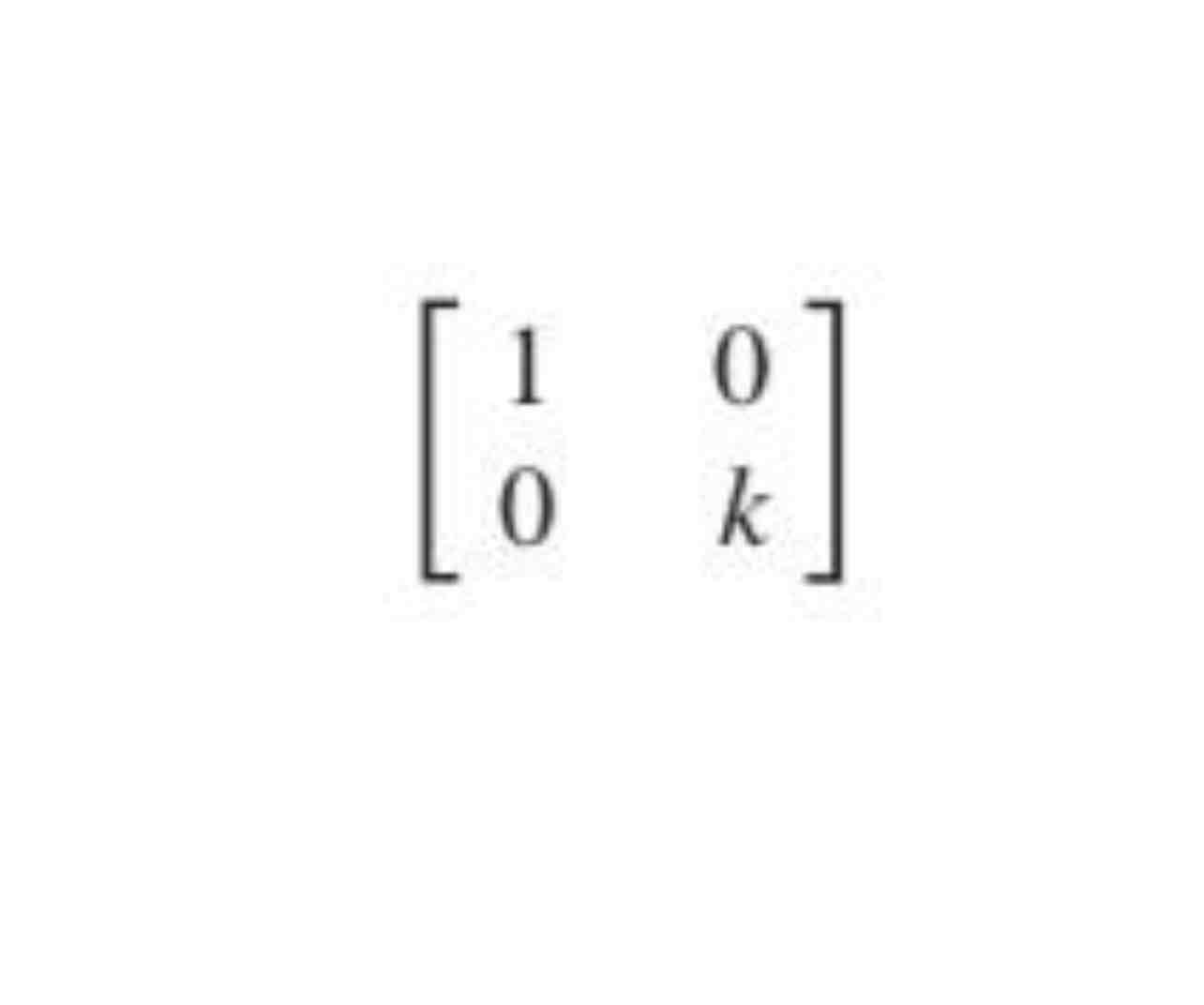
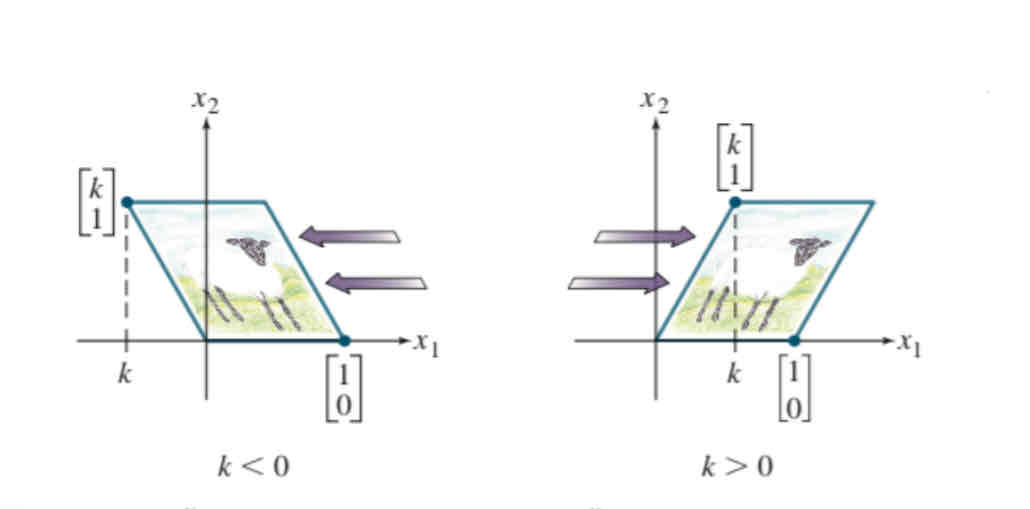
Horizontal shear

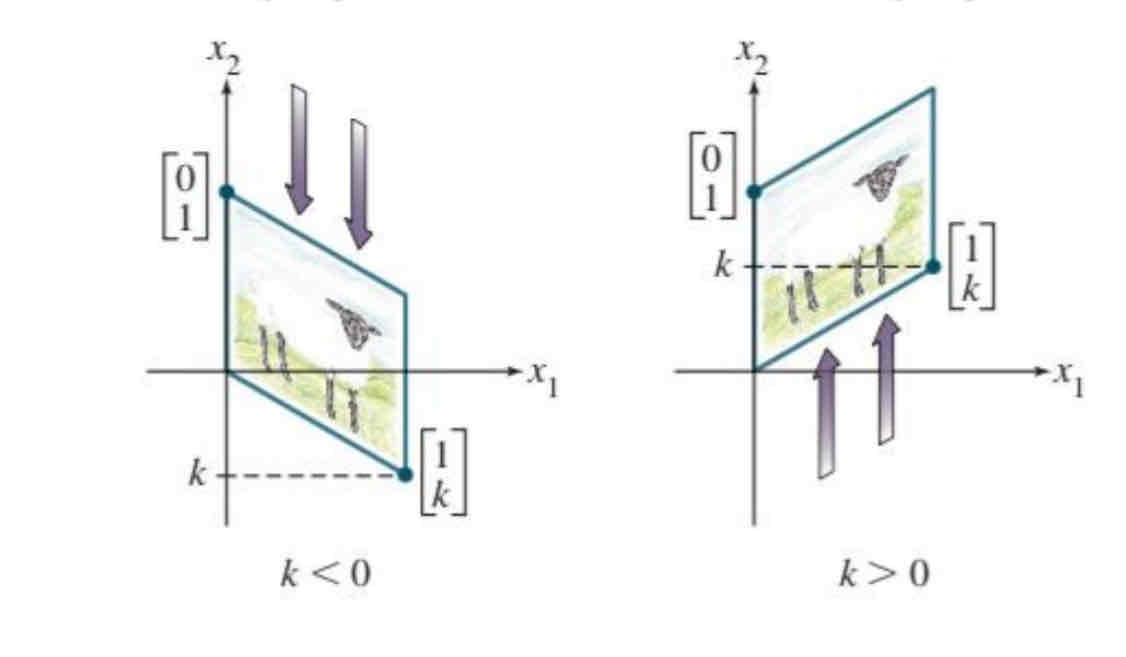
Vertical shear

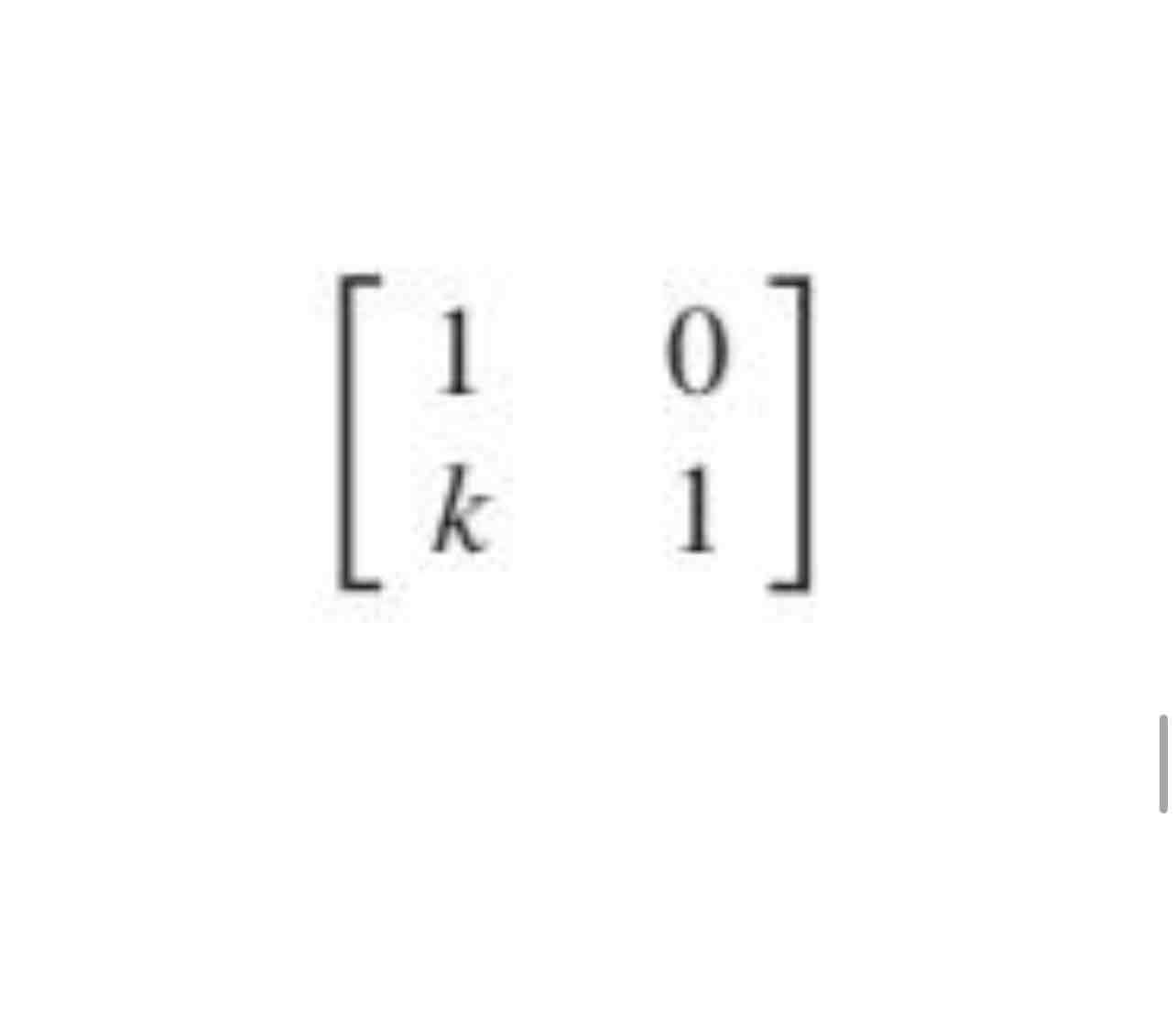
Onto Transformation

A transformation T: R^n ➡R^m is said to be onto R^n if each b in R^m is the image at least one x in R^n

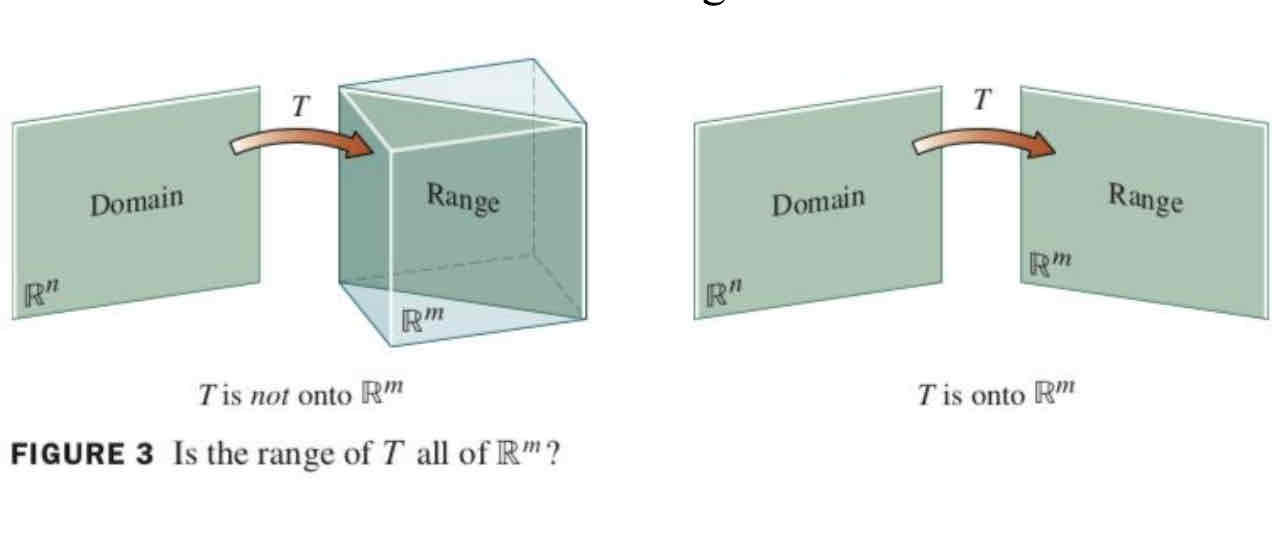
How do we know if the transformation is onto?

Theorem 4

• Ax=b has a solution for all b in R^m

• Each b is a linear combination of the columns of A

• The columns of A span R^m

• Matrix A has a pivot position in every row

One to one transformation

A transformation T: R^n ➡R^m is one to one if each vector b in R^m is the image of at most 1 vector x in R^n

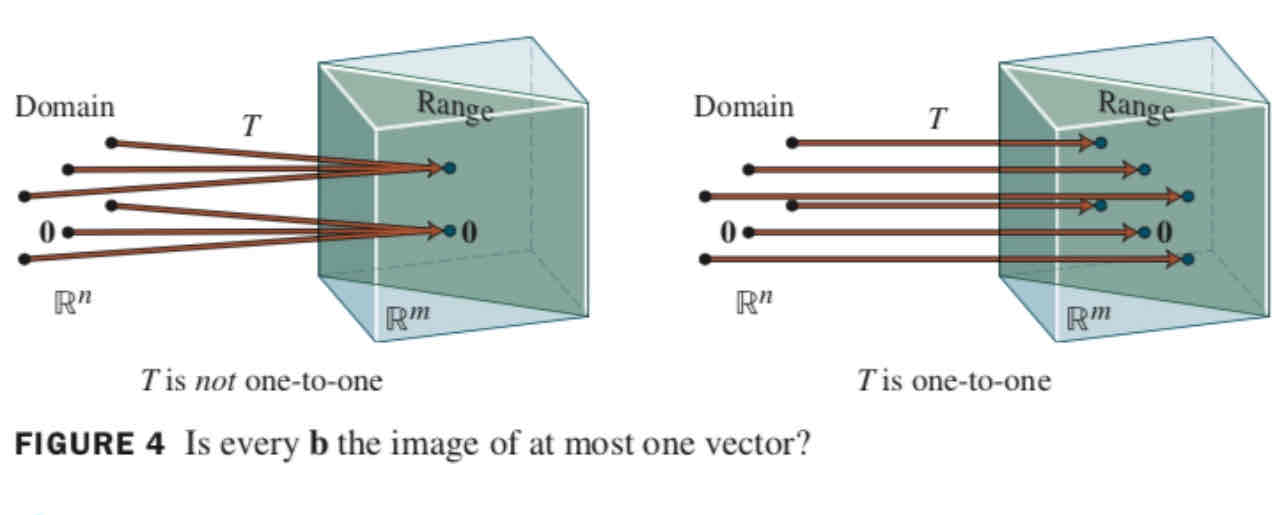
How do we know if the transformation is one to one?

The solution has to be a unique solution

• No free variables

• Pivot positions in every column

• The equation T(x) = 0 has only the trivial solution

• The columns of A are linearly independent