Measure of variability Range, standard deviation, variance

Range, standard deviation, variance

Why do we need variability measures?

• because the variability in two data might be quite different

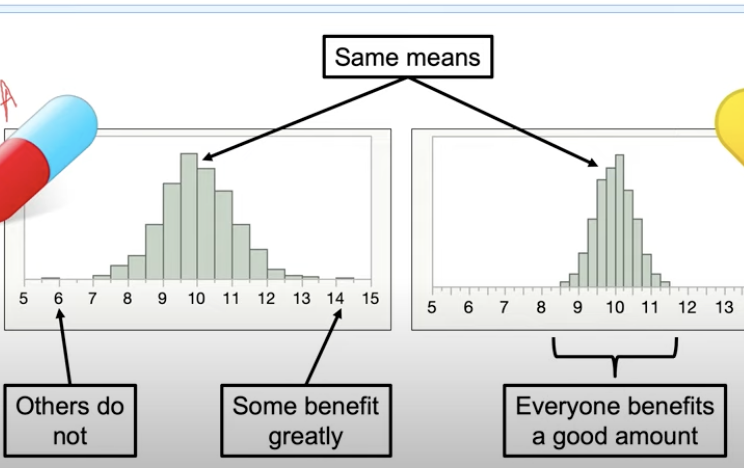
how can we describe these differences statistically? (measures of variability)

• in statistics, measure of variability describe how scores in a given dataset differ from one another (e.g. the spread or clustering of points)

Three types of measuring of variability

• Range

• Standard deviation

• Variance

Range

• is the simplest measure of variability (or dispersion)

Formula of range

r = h - l

r = the range

h = highest score in a data set

l = lowest score in a data set

Calculating the range

• subtracting the highest score from the lowest score

• 

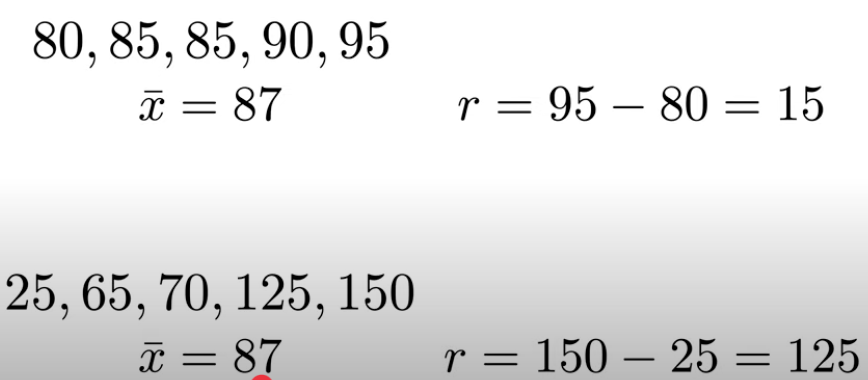
what can we say about the mean and the range?

the mean of 87, and the range of 15 describes a very different situation compared to the mean of 87 and the range of 125

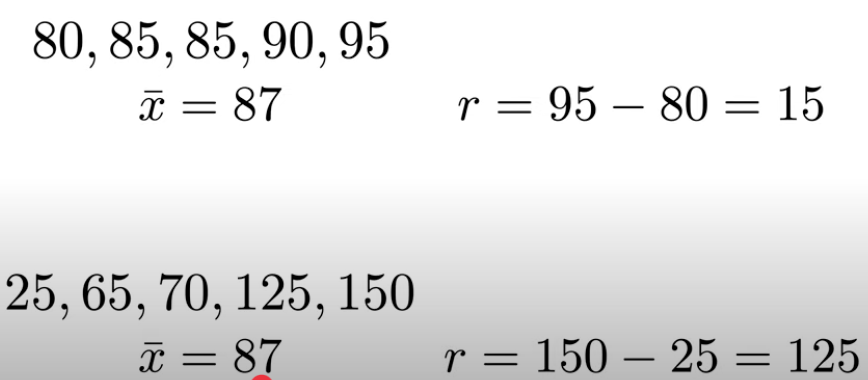
Limitation of range

although using the range is effective, we might miss important information of the data set

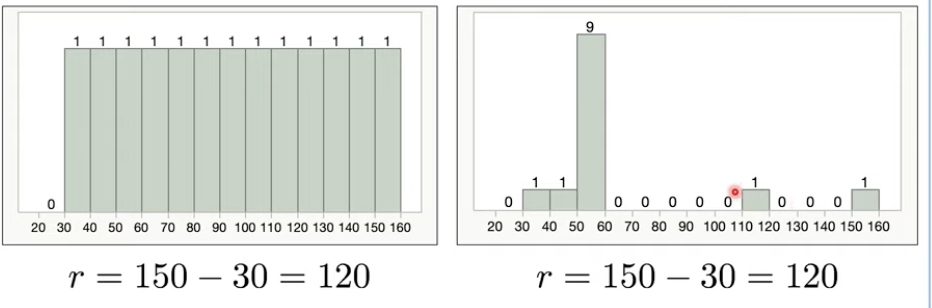
we can not be sure if the data looks like the first histogram or the second, thus we can use standard deviation.

Standard Deviation

• standard deviation or typical amount that scores deviate from the mean

sigma (sigma with little s)

• standard deviation of a population

s

• standard deviation of a sample

standard deviation of population

sigma (written with little s)

standard deviation of sample

little “s”

Why is standard deviation useful?

• when we have a normal distributed data, standard deviation have interesting poverty of information which can emphasise what is common and what is uncommon

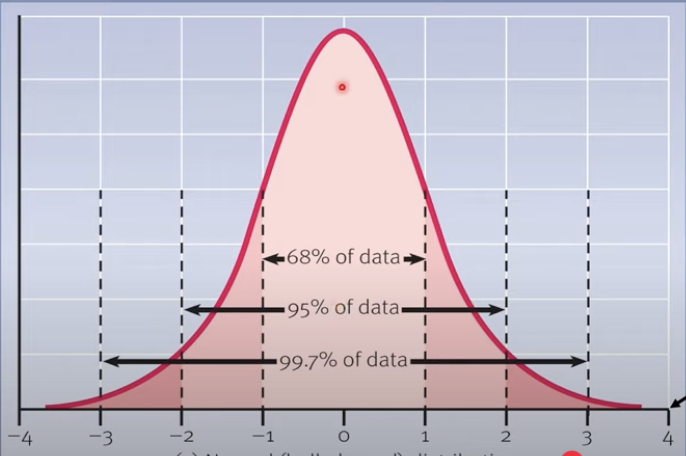
0 is the mean

zero standard deviation is straight up from the zero

1 = is one standard deviation above the mean

-1 = is one standard deviation below the mean

= 68 % of the people will fall between the range of -1 & 1

(one standard deviation from the mean)

How many percent of people will fall between the deviations of -2 & 2?

• the standard deviation between -2 & 2 is 95%.

• 95% of the people fall between -2 & 2 (two standards deviation from the mean).

How many percent of people will fall between the deviations of -3 & 3?

• The standard deviation between -3 & 3 is 99,7%

• 99,7% of people are falling between -3 & 3 (three standard deviation from the mean) - this is more rare data

Variance

• the averaged squared deviation from the mean

• (e.g. the square of standard deviation from the mean)

Variance of samples

• s squared

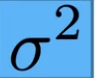
Variance of population

• sigma squared

Variance of sample

squared s

Variance in population

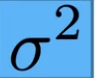
squared sigma

Population Parameter standard deviation

• 

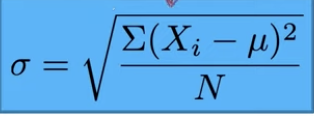
• Sigma on the left

• the numerator is called sums of squares/SS

• each x value is subtracted by the mean of all the values

• squaring that value

Population Parameter variance

• each x value is subtracted by the mean of all the values

• squaring that value

formulas sample statistic standard deviation

• s on the left

• each x value is subtracted by the mean of all the values

• squaring that value

Formula sample statistic variance

Calculation of

• find the index number (xi) (e.g. x1 …. x10)

• add all numbers of the variable up and divide by the amount of number which was added, to find the mean (e.g. x-bar = 2.6)

• Subtract each value from the mean (xi — x-bar) (e.g. 2 - 2,6 = -0.6)

  

• Then square the all the values in xi — x-bar: “square -0.6” which then equals 0.36

  

  • then sum up ∑(xi-x—bar)uppercase2 = 22,4

  • This is referring to the sum of squares, or SS

next:

have in mind:

— ∑(xi-x—bar)uppercase2 = 22,4

— n ‹ represents the sample size (in this case 10)

(n-1 = 10-1 = 9)

This means:

22.4/ 9 = 2.49

the sample variance is 2.49

The sum of squares, or SS

represents the sum of squared deviations from the mean

in every process start to:

• subtract the mean from each value

• square it

• add up all the values in the last column, which will give you the result of the SS/ the sum of squares

• sample standard deviation means the square root of the variance

• in this case √2.49 = 1,58

• The sample standard deviation is 1,58

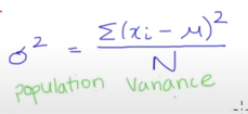
• finding the population variance

• first, use the sums of squares SS (in this case 22.4)

• Divide the SS= 22,4 by the population size (in this case 10)

• N = 22,4/10 = 2,24

• Population variance is 2,24

• square root of the population variance to find the standard deviation of population

• In this case √2,24

• The standard deviation of the population is 1,5