Calculus Derivative Guide

5.0(1)
learnLearn
examPractice Test
spaced repetitionSpaced Repetition
heart puzzleMatch
flashcardsFlashcards
Card Sorting

1/35

encourage image

There's no tags or description

Looks like no tags are added yet.

Study Analytics
Name
Mastery
Learn
Test
Matching
Spaced

No study sessions yet.

36 Terms

1
New cards

Derivative of sin x

cos x

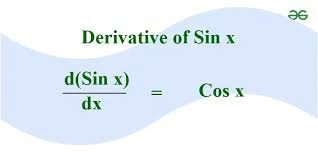
<p><sup>cos x</sup></p>
2
New cards

Derivative of cos x

-sin x

<p>-sin x</p>
3
New cards

Derivative of tan x

sec2 x

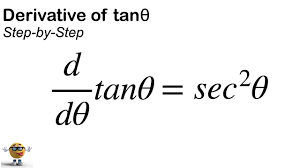
<p>sec<sup>2 </sup>x</p>
4
New cards

Derivative of cot x

-csc2 x

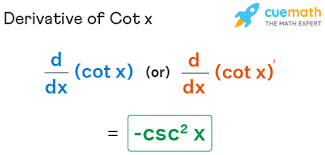
<p>-csc<sup>2 </sup>x</p>
5
New cards

Derivative of sec x

sec x tan x

<p>sec x tan x</p>
6
New cards

Derivative of csc x

-cot x csc x

<p>-cot x csc x</p>
7
New cards

Derivative of ex

ex

<p>e<sup>x</sup></p>
8
New cards

Product Rule

f(x)*g’(x) + g(x)*f’(x)

<p><span>f(x)*g’(x) + g(x)*f’(x)</span></p>
9
New cards

Quotient Rule f(x) / g(x)

(g(x)*f’(x) - f(x)*g’(x)) / (g(x))2

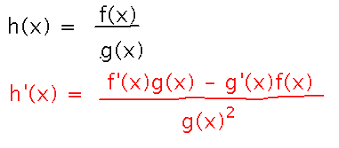
<p><span>(g(x)*f’(x) - f(x)*g’(x)) / (g(x))</span><sup>2</sup></p>
10
New cards

Power Rule (derivative of xn)

nxn-1

  • xÂł=3x²

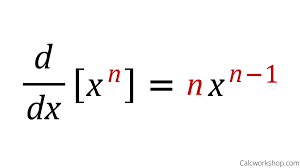
<p>nx<sup>n-1</sup></p><ul><li><p>x³=3x²</p></li></ul><p></p>
11
New cards

Constant Rule (derivative of a constant)


0

  • 5=0

  • pi=0

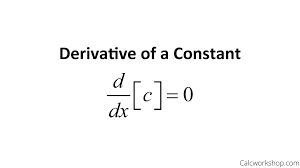
<p><br>0</p><ul><li><p>5=0</p></li><li><p>pi=0</p></li></ul><p></p>
12
New cards

Constant Multiple Rule (cf(x))

cf’(x)

  • 5x4=20xÂł

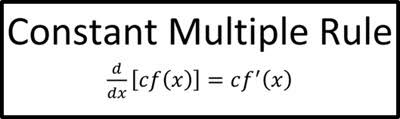
<p>cf’(x)</p><ul><li><p>5x<sup>4</sup>=20x³</p></li></ul><p></p>
13
New cards


Sum and Difference Rules (derivative of f(x) ± g(x))


f’(x) ± g’(x)

  • x4+3x2-1 = 4x3+6x

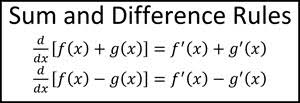
<p><br>f’(x) ± g’(x)</p><ul><li><p>x<sup>4</sup>+3x<sup>2</sup>-1 = 4x<sup>3</sup>+6x</p></li></ul><p></p>
14
New cards

Derivative of sin-1 x

1 / sqrt(1 - x2)

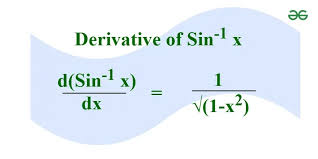
<p>1 / sqrt(1 - x<sup>2</sup>)</p>
15
New cards

Derivative of cos-1 x

-1 / sqrt(1 - x2)

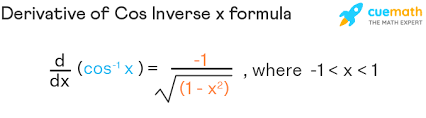
<p>-1 / sqrt(1 - x<sup>2</sup>)</p>
16
New cards

Derivative of tan-1 x

1 / 1 + x2

<p>1 / 1 + x<sup>2</sup></p>
17
New cards

Derivative of cot-1 x

-1 / 1 + x2

<p>-1 / 1 + x<sup>2</sup></p>
18
New cards

Derivative of sec-1 x

1 / |x|*sqrt(x2 - 1)

<p>1 / |x|*sqrt(x<sup>2</sup> - 1)</p>
19
New cards

Derivative of csc-1 x

-1 / |x|*sqrt(x2 - 1)

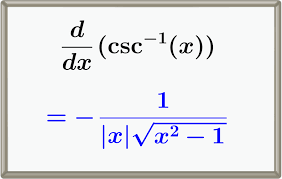
<p>-1 / |x|*sqrt(x<sup>2</sup> - 1)</p>
20
New cards

Chain Rule f(g(x))

f’(g(x))*g’(x)

<p>f’(g(x))*g’(x)</p>
21
New cards

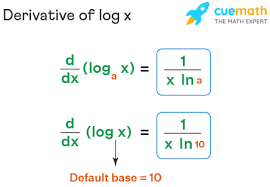
Derivative of ln x or loge x

1 / x

<p>1 / x</p>
22
New cards

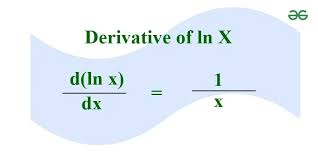
Derivative of loga x

1 / x*ln n

<p>1 / x*ln n</p>
23
New cards

Implicit Rule (dy/dx (x2+y2=25)

2x + 2y*y’ = 0

y’ = -x / y

<p>2x + 2y*y’ = 0</p><p>y’ = -x / y</p>
24
New cards

Expanding Rule (3Ă—2 + 1)2

(3Ă—2 + 1)*(3Ă—2 + 1)

(9Ă—4 + 6Ă—2 + 1)

y’ = 36×3 + 12x

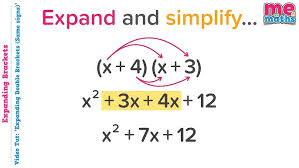
<p>(3×<sup>2</sup> + 1)*(3×<sup>2</sup> + 1)</p><p>(9×<sup>4</sup> + 6×<sup>2</sup> + 1)</p><p>y’ = 36×<sup>3</sup> + 12x</p>
25
New cards

Outside-Inside Rule (3Ă—2 + 1)2

(3Ă—2 + 1)2

y’ = 2(3×2 + 1)*6x

y’ = 36×3 + 12x

<p>(3×<sup>2</sup> + 1)<sup>2</sup></p><p>y’ = 2(3×<sup>2</sup> + 1)*6x</p><p>y’ = 36×<sup>3</sup> + 12x</p>
26
New cards

U - Substitution (3Ă—2 + 1)2

(3Ă—2 + 1)2

y’ = 2u * 6x

y’ = 2(3×2 + 1)2 * 6x

y’ = 36×3 + 12x

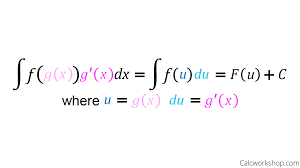
<p>(3×<sup>2</sup> + 1)<sup>2</sup></p><p>y’ = 2u * 6x</p><p>y’ = 2(3×<sup>2</sup> + 1)<sup>2 </sup> * 6x</p><p>y’ = 36×<sup>3</sup> + 12x</p>
27
New cards

|x| is equivalent to

Sqrt(x²)

28
New cards

Derivative of ax

ax * lna

29
New cards

Derivaticve of lnex or elnx

x

30
New cards

y = logb x is equivilant to

by = x

31
New cards

y = log10 x is equivilant to

y = log x

32
New cards

y = loge x is equivilant to

y = ln x

33
New cards

When logb(xy)

logb x + logb y or ln x + ln y becauce bm * bn = bm+n

34
New cards

When logb(x/y)

logb x - logb y or ln x - ln y becauce bm/bn = bm-n

35
New cards

When logb xp

P * logb x or P * ln x becauce (bm)n = bm*n

36
New cards

Derivative lny = any function

y*(derivative of that function

Explore top notes

Explore top flashcards