Maths March Assessment: important things to remember

formula for probability of an event when all the outcomes are equally likely

number of ways the event can happen
total number of possible outcomes

Mutually exclusive events

events that can’t happen at the same time e.g. rolling a 1 and rolling a 3 on one dice roll.

Independent events

events that have no effect on the probability of each other

P(event A and event B) for independent events

P(A) x P(B)

P(event A or event B) for mutually exclusive events

P(A) + P(B)

P(event A or event B) for non mutually exclusive events

P(A) + P(B) - P(A and B)

Dependent / conditional events

events that depend / are influenced by other events

opposite of independent events

function for and in probability generally speaking

multiply

function for or in probability generally speaking

add

Arithmetic sequences (aka linear sequences)

terms increase or decrease by the same value each time

Geometric sequence (aka geometric progressions)

consecutive terms are found by multiplying/dividing by the same value (called the common ratio)

nth term of an arithmetic/linear sequence

bn + a

where a = the difference between the terms

and b = the term with n = 0 (the one before the first one)

nth term of a geometric sequence

a x r^n-1 where a is the first term of the sequence and r is the common ratio

nth term of a quadratic sequence

1. Work out the difference between each pair of terms

2. Work out the second difference - the difference between the differences.

3. Divide the second difference by 2 to get the coefficient of the n² term. Write this down.

4. For each term in the sequence, work out the coefficient of the n² term you just worked out, subbing 1, 2, 3 etc into n for each term.

5. Now subtract those numbers you just worked out from each term in the original sequence (term - coefficient) to give a new sequence

6. Work out the nth term of this new sequence, and simply add it onto the end of the coefficient you worked out in step 3.

form of linear graphs

y = mx + c where m is the gradient and c is the y-intercept

form of quadratic graphs

ax² + bx + c where c is the y-intercept

what do quadratic graphs look like

parabola: u-shape

1 turning point

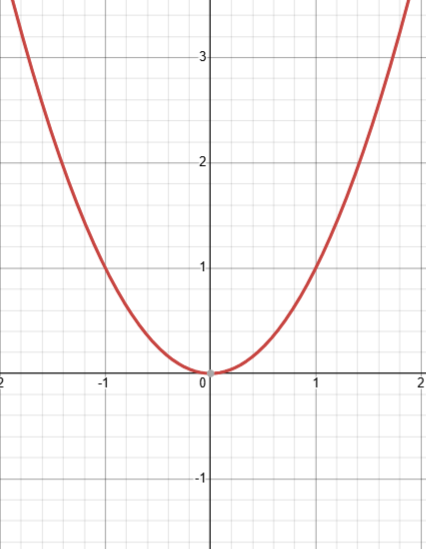
how to find the roots of a quadratic or cubic equation from its graph

they are the points at which the graph crosses the x-axis

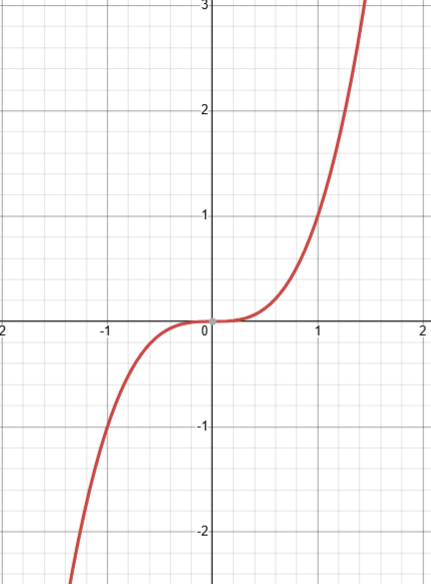
form of cubic graphs

ax³ + bx² +cx + d

what do cubic graphs look like

curve with a wiggle in the middle

2 turning points

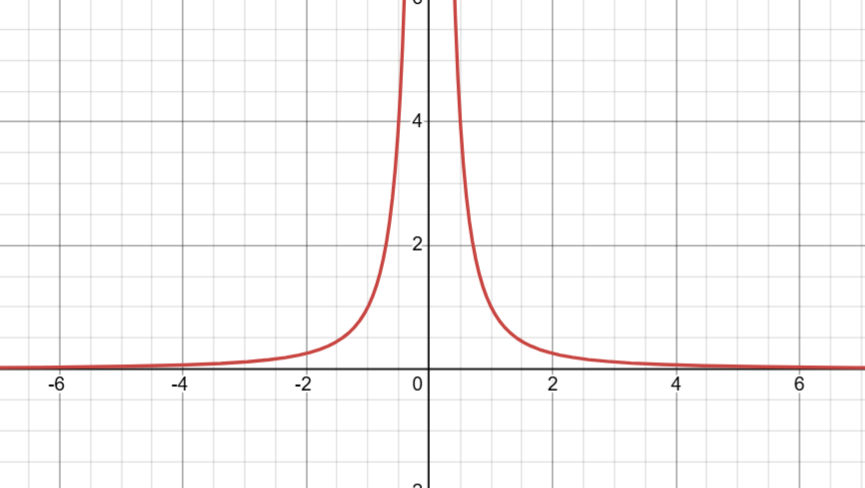
form of reciprocal graphs

a
f(x)

f(x) means that y is some function of x, such as x+1

you can recognise them by their fraction

asymptotes of reciprocal graphs

denominators of reciprocals can never equal 0, if it does the function is undefined

asymptotes are lines that the graph gets very close to but never touches.

what happens if a reciprocal term is squared

it will only have positive values so the graph will look like this

form of exponential graphs

y = a^x (where a > 0)

when a is bigger than 1 the graph increases really quickly

when a is smaller than 1 the graph decreases really quickly

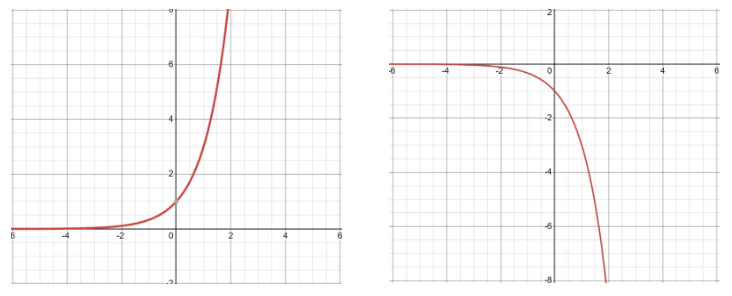
what coordinate do all exponential graphs go through

(0, 1)

form of circle graphs

(x - a)² + (y - b)² = r²

r is the radius

the centre is (a, b) but with the opposite signs than the numbers in the equation

give this a look bestie :)

1 tonne in kg

1000kg

ml - cm³

1ml = 1cm³