lec 6: biostats 2 (gonzalez)

deciding on a statistical test

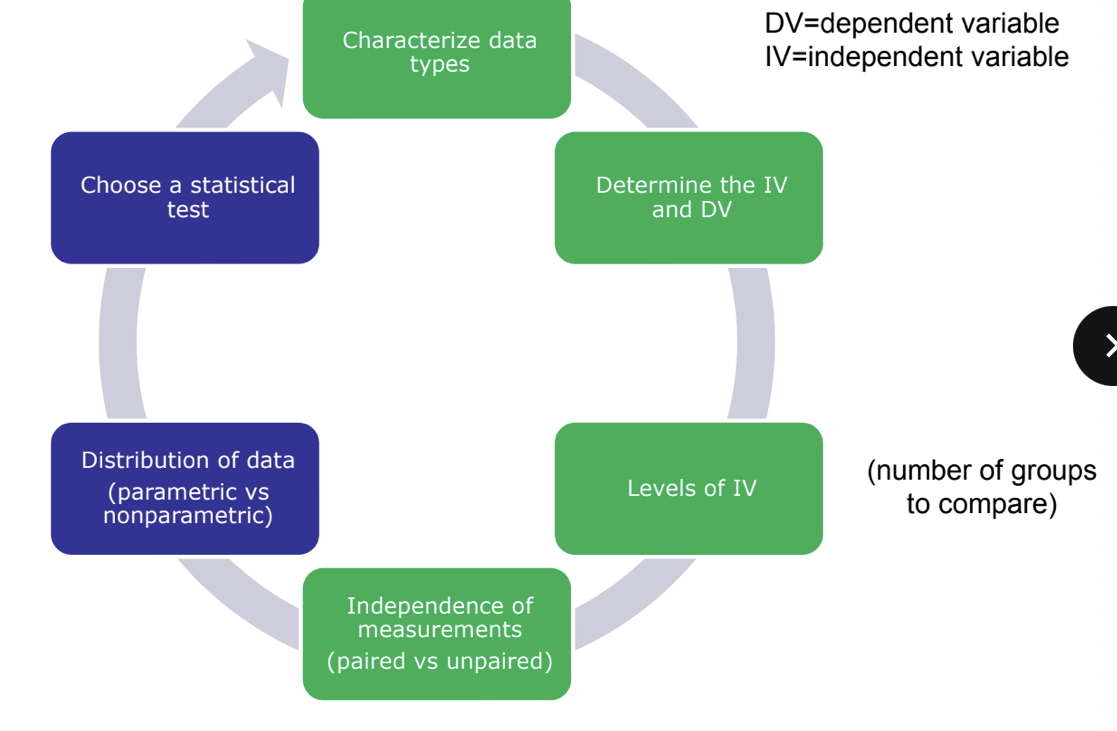
data distribution - parametric or NOT?

parametric tests

• only valid when the characteristic studied follow a normal distribution in the population (bell shaped curve) or close to normally distributed

• can be applied to most continuous data

  • prefer b/c higher power

non-parametric tests

• applied to non-normally distributed data or data that do NOT meet the criteria (assumptions) for use of parametric tests

• parametric tests have more assumptions; these tests have more power

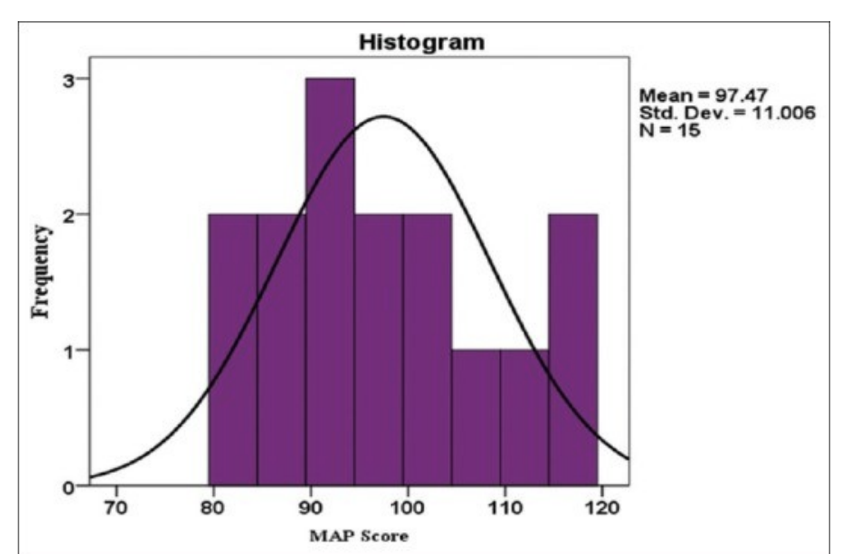
how to determine data normality

statistical testing

• kolmogrov-smirnov test

  • used for n ≥50

• shapiro-wilk test

  • more approrpriate method for small sample sizes (<50 samples)

• when P>0.05 → data caled as normally distributed

• can visually inspect the histogram

• skewness or kurtosis

  • a distribution is called approximate normal is skewness or kurtosis (excess0 of the data are between -1 and +1

• mean = median

  • if this is true, then data perfect

non-normal distribution

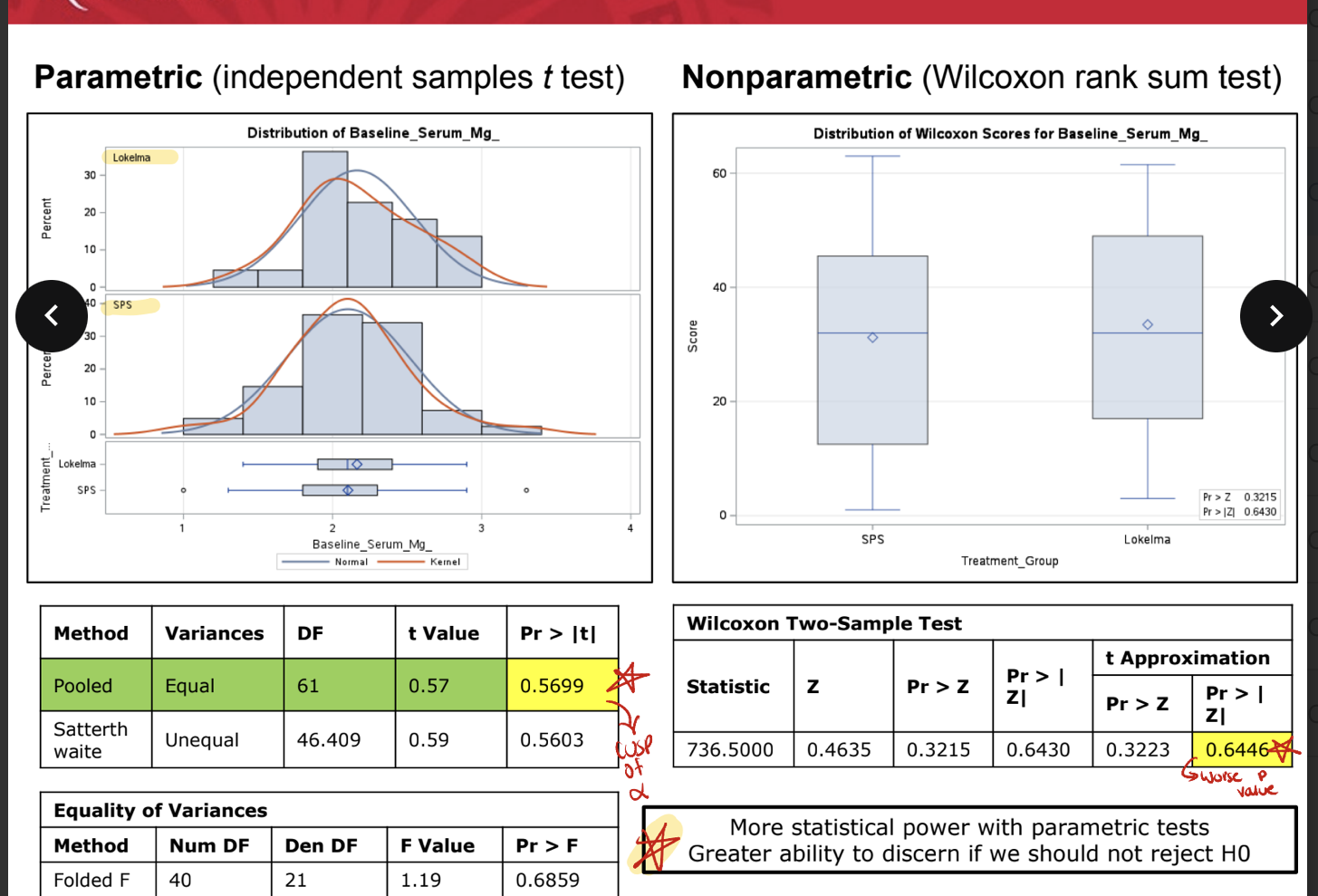
parametric vs nonparametrc

more statistical power with parametric tests; greater ability to discern if we should not reject Ho

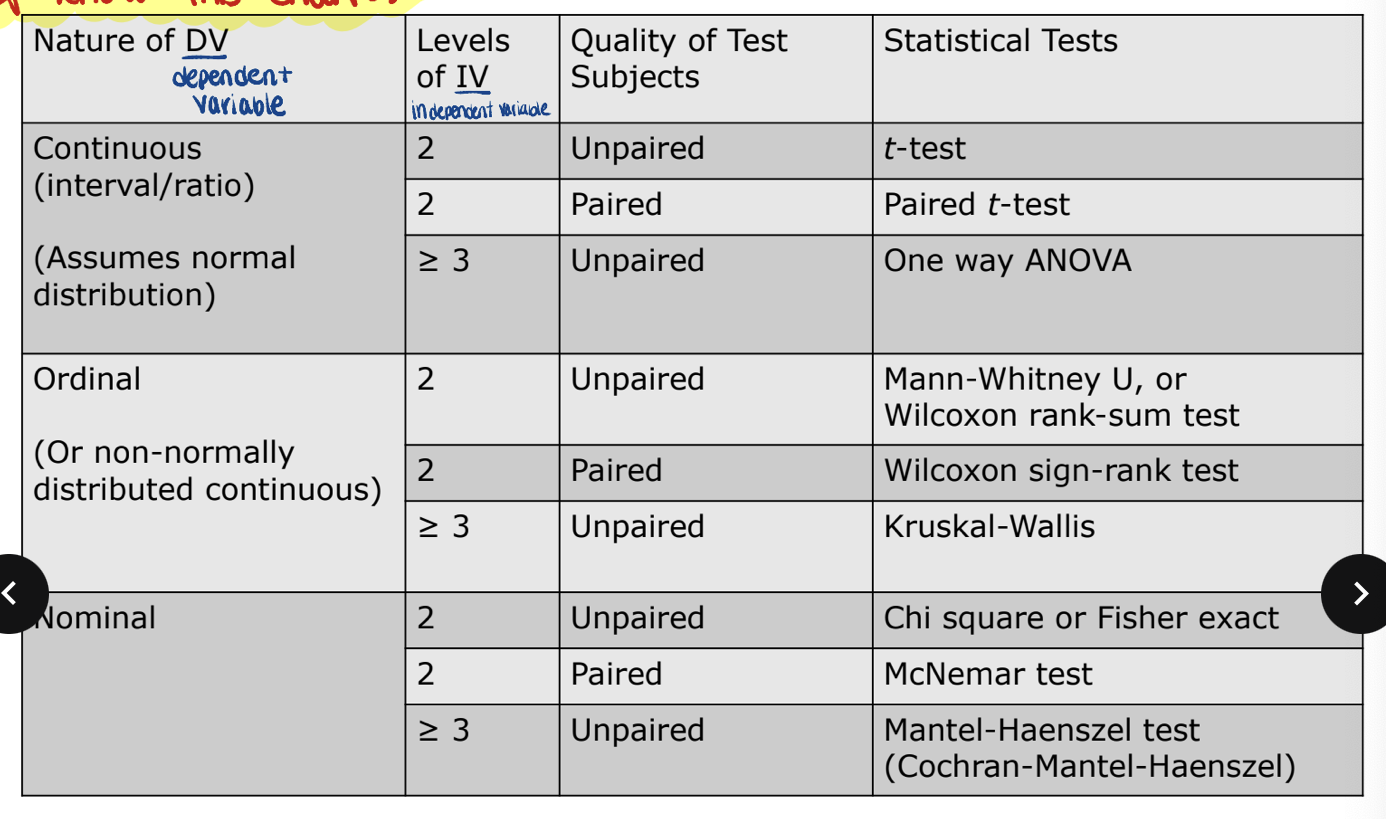
know this fucking chart

parametric tests *

T test

• method of chooice when making a single comparison between 2 groups whose data meet the assumptions required of parametric analysis

student’s T test

• most powerful of the statistical tests designed for use with interval data

• intended for use in analyzing data from 2 independent samples

• assumptions

  • 2 samples are random samples drawn from independent populations

  • variable is approximately normally distributed and continuous

  • measured on interval or ratio scale

  • variances of the groups are similar

paired T test

• analyzes results in dependent or related data

• violation of first assumption

ANOVA (4 groups)

• specifically designed for comparing data from 3 or more groups

• partition the variance in a set of data into various components

• test determines the contribution of each component

  • total variance for the complete data set

  • variance within each group of the data set (error variance)

  • variance between each group within the data set

• does NOT indicate which groups differ

• assumptions

  • each of the groups is a random sample from the population

  • measured variable is continuous

  • variable is ratio or interval scale

  • error variances are equal

  • variable is normally distributed

• different ANOVA tests are available depending on the type of data (ordinal vs interval) and whether the samples are independent or related

• if a difference is found, additional tests can be applied (bonferroni t test, neuman keuls test, dunnet test, duncan multiple range test, tukey test, sheffe test)

what is a bonferroni correction *

• compensates for multiple comparisons by dividing the significance level by the # of comparisons

• a significance level of 0.05 is commonly accepted

  • but… if study tested 5 comparisons there would be up to a 22.3% likelihood that any one of them would show a significant difference be chance → high (for type 1 error risk)

• to correct for this potential concern → reduces risk of type 1 error

• for the example above, new p-value threshold would be 0.01

non-parametric

chi square

• commonly encountered

• used for nominal data

• intended for data derived from independent samples

• analysis is performed most often with a 2×2 table

• minimum sample size = 20 (5 in each cell)

fisher’s exact

• similar to chi square

• useful for sample size <20 or sample size 20-40 when any cell has a value 

mcnemar test (paired or match data)

• used when you CANNOT use chi square b/c of violataion of independence

• used with paired or matched data

• applied to nominal data

• paired version of chi test

mantel-haenszel test

• analyze stratifid data to deal with confounding factors

mann-whitney U

• applied to ordinal data

• used for data derived from independent samples

wilcoxon signed rank test

• used when related samples exist

• use when NOT normally distributed, NOT interval/ratio data, or variances are different

• rank scores and then examine the relative ranks for each score

• preferred over sign test b/c it reflects the magnitude of difference between pairs

kruskal-wallis test one-way anova

• used when 3 or more groups are compared and when subjects are NOT permitted to participate in more than one group

• extension of the mann-whitney U test

• variables at least measured on ordinal scale

• used with independent samples

• non-parametric counterpart to ANOVA

friedman test

• used when subjects participate in 3 or more treatment groups

• applies to data that are ranked and organized

• useful when a 2-way ANOVA CANNOT be used

choosing the correct test

what info do you need to decide?

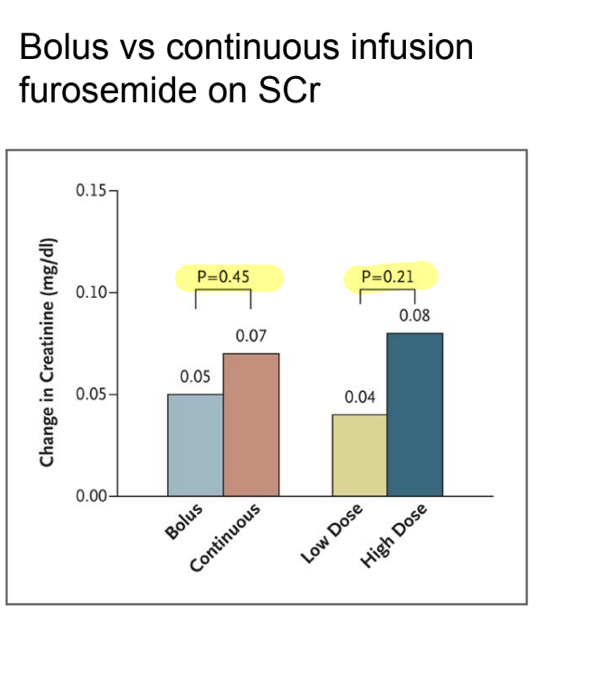
• IV → bolus vs cont. infusion

• DV → change in serum creatinine and is a continuous variable

assuming normality, what test would you use?

T test

simple correlation

• indicates quantitiative strenght of relationship between 2 continuous variables

  • height and weight; exercise time and HDL

• generates co-efficient from -1 to +1

  • negative to positive relationship

  • 0 means NO correlation at all

• parametric = pearson’s correlation

• non-parametric = spearman’s rho

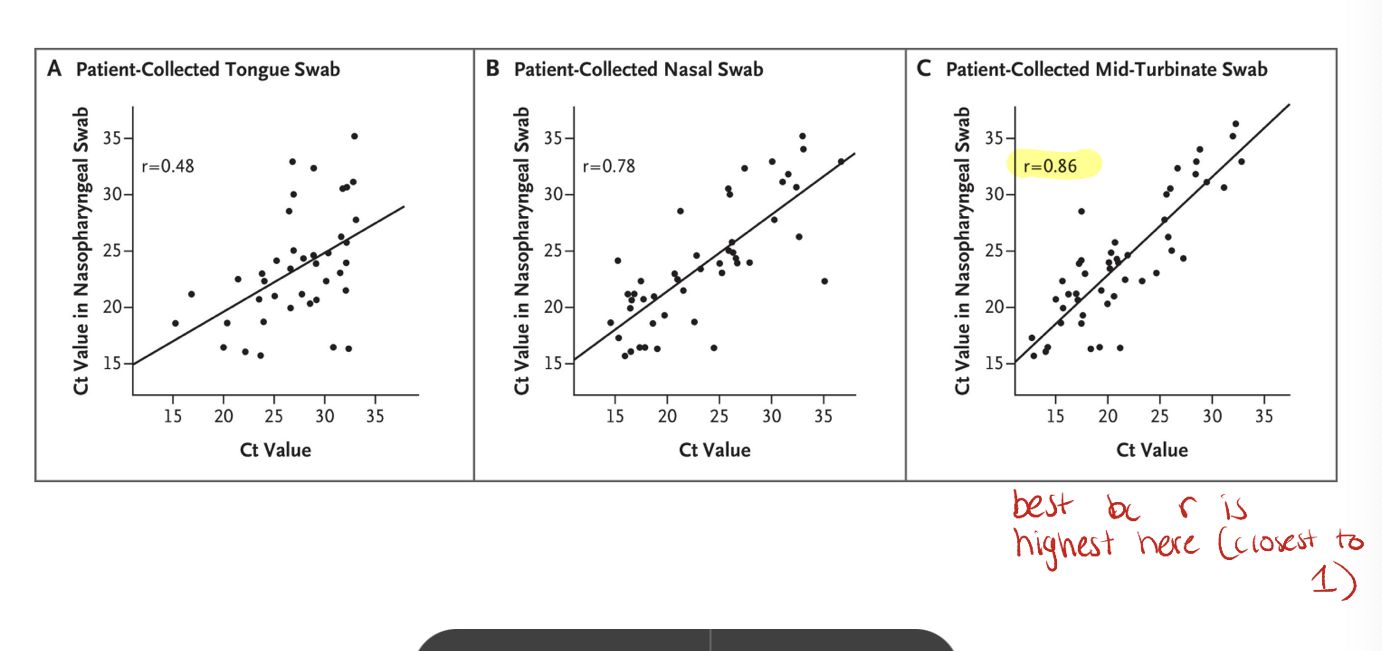
sample correlation

comparison of cycle threshold (Ct) values for COVID swabs from various sites vs nasopharyngeal swab

simple linear regression

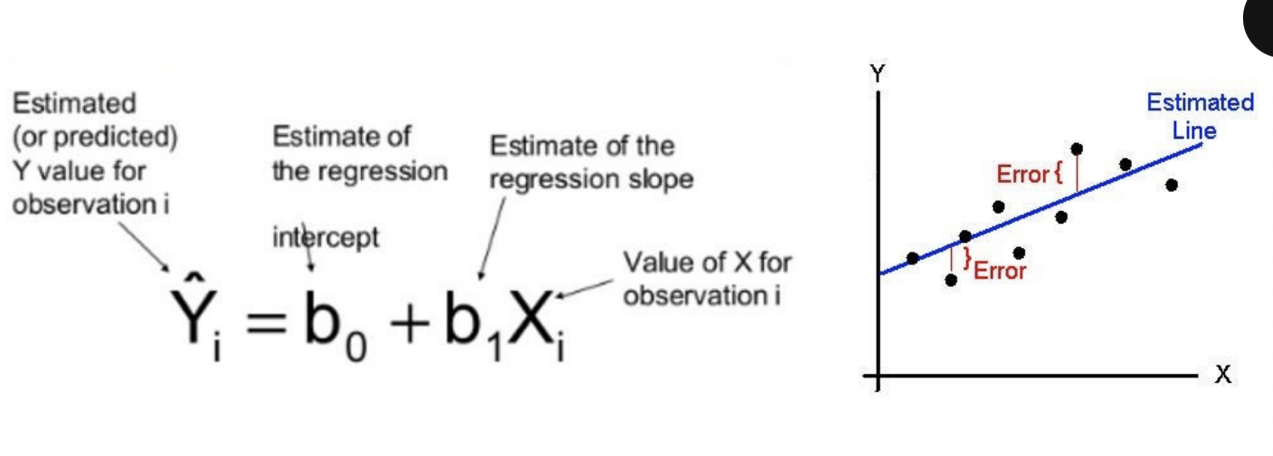
• regression → prediction of outcome (DV) using input variables (IVs)

• linear regression fits a line to data by the ‘least squares’ method

• model generate coefficients (slopes) quantifying strength of prediction for outcome

  • slope needs to be nonzero for significance

  • slope related to proportional change in output

• parametric testing

  • assumes continuous variables, independence of data, linearity, homoscendasticity, normal distirbution

  • uses a least-squares line thru data to minimize error sum of squares

linear regression example

logistic regression

• regresssion model where outcome is nominal (yes/no)

• fits an S-shaped logistic function of probability

  • based on logit probability

  • log odds (hence logistic regression)

• uses a max likelihood function to fit function

• generates coefficients/slopes with similar interpretation as linear regression

  • can be interpreted as odds ratio (ORs)

  • know how to interpret coeff

data presentation alters perception

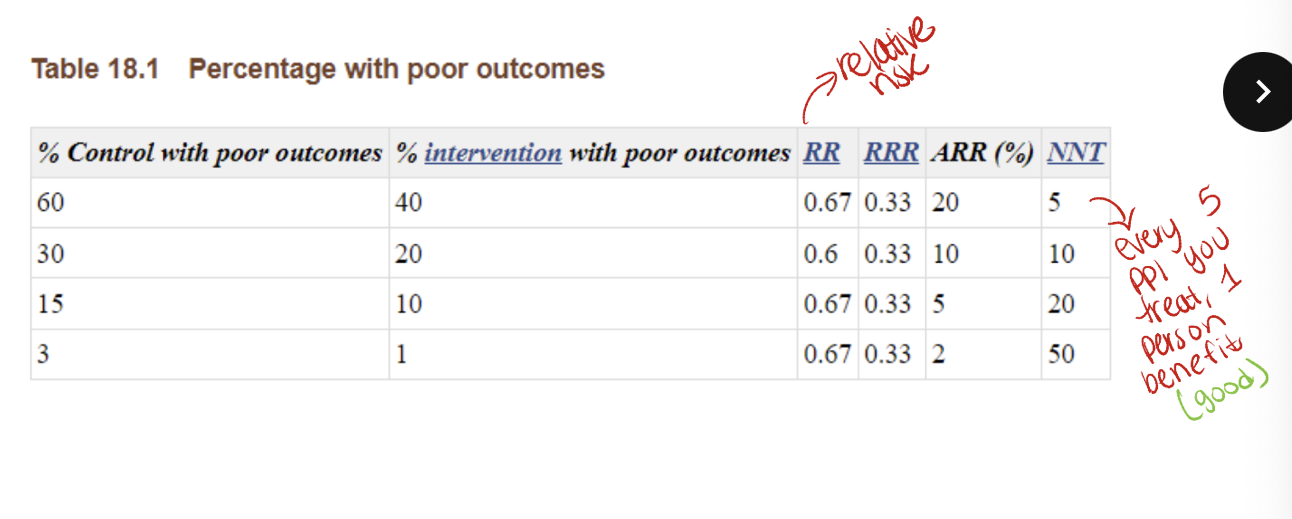
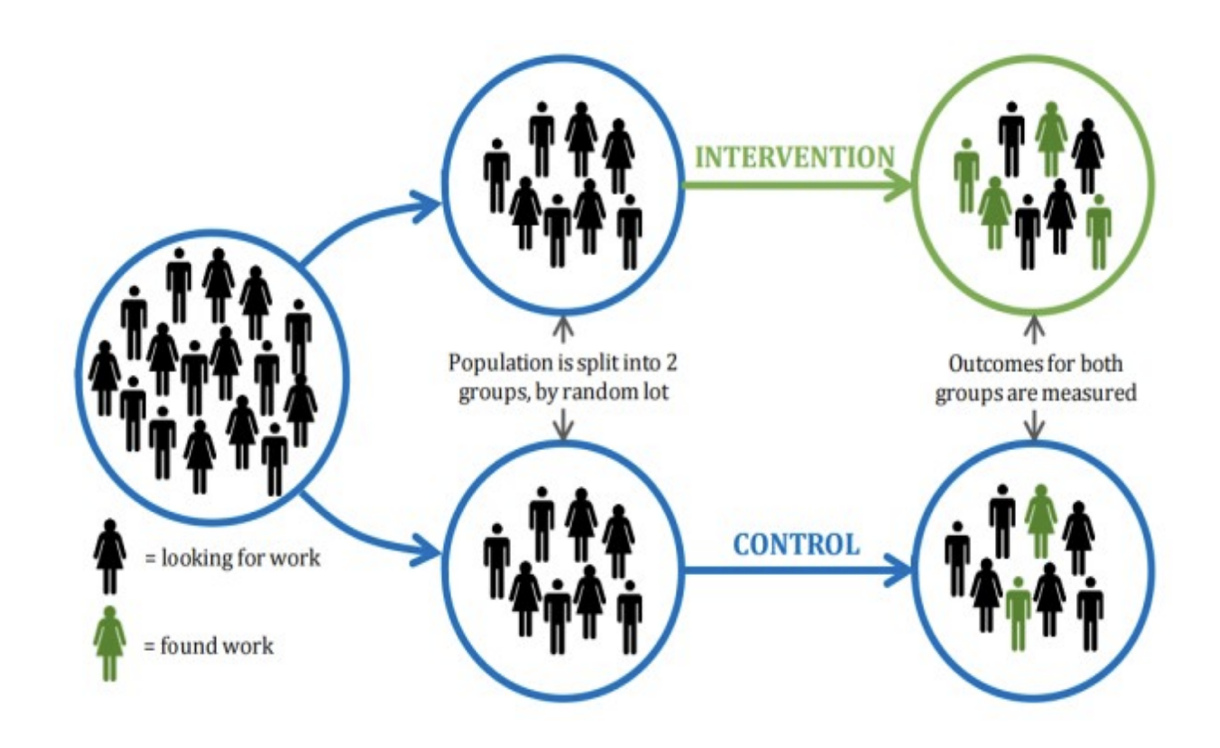
example RCT

outcomes

experimental group → 90/100 will find work

control group → 60/100 will find work

risk/rate → 90% vs 60%

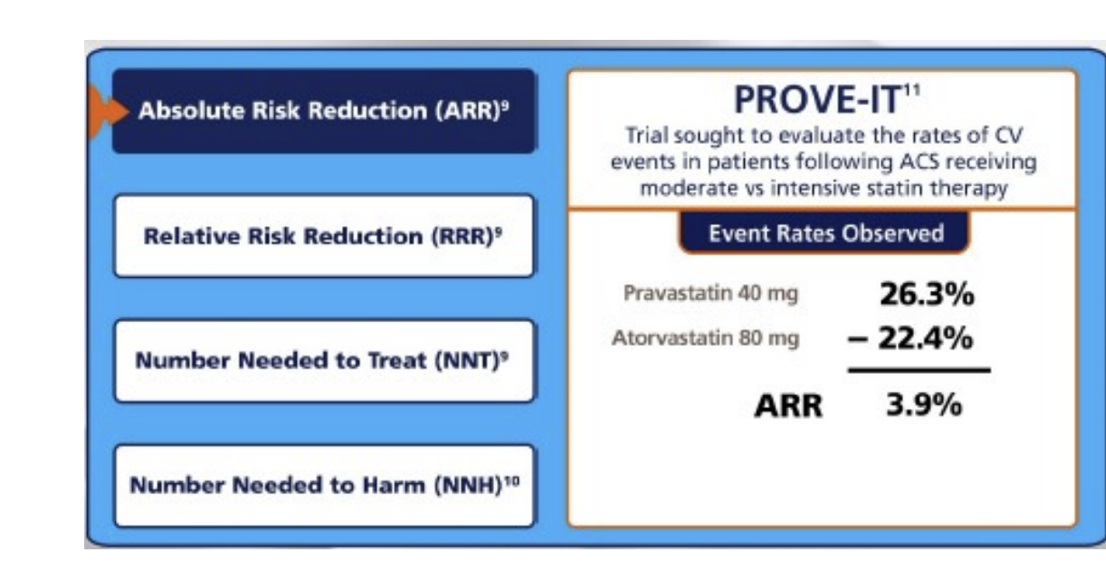
absolute risk reduction

know this: ARR= EER-CER

• EER = experimental event rate

• CER = control event rate

relative risk reduction

number needed to treat/harm

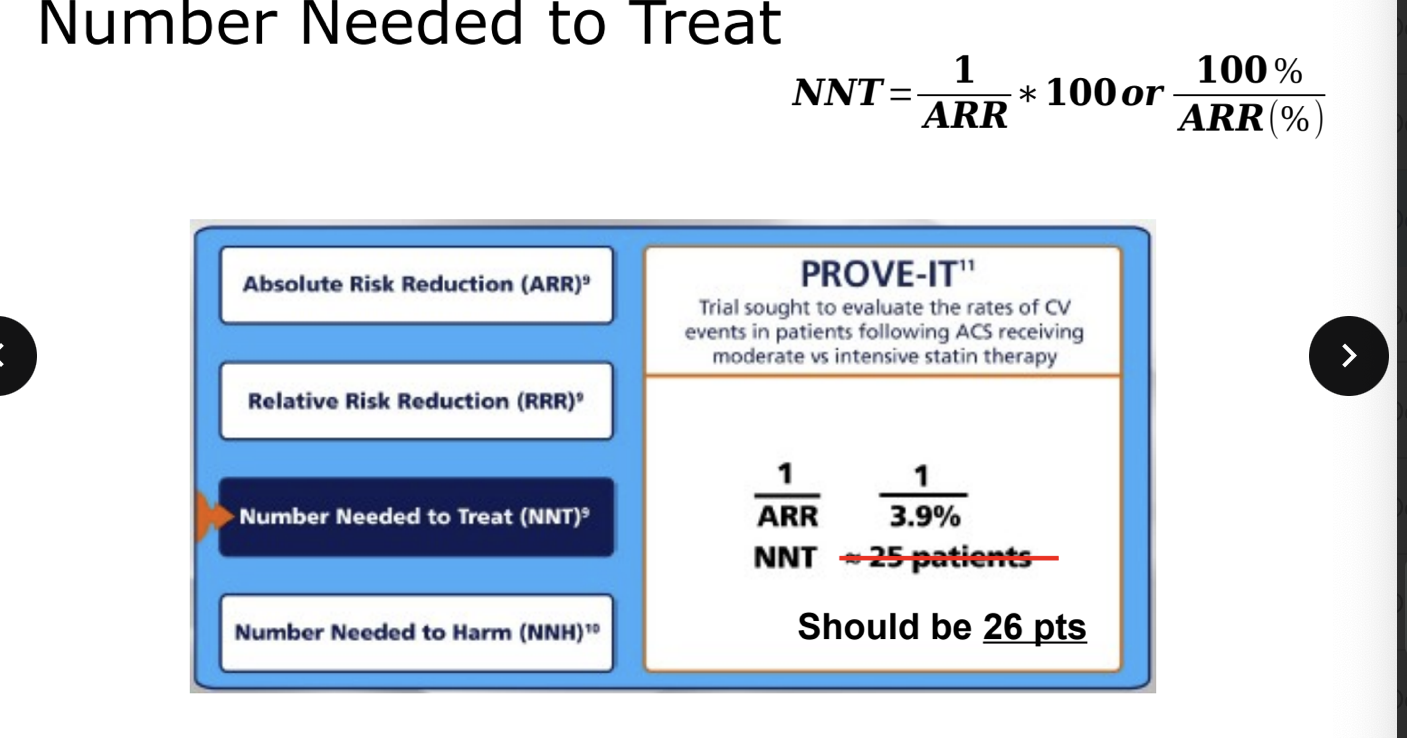
number needed to treat (NNT)

• # of patients who need to be treated for a certain period of time in order for 1 patient to benefit

• photo = formula

• always round up

• for every X patients who receive treatment for 1 year, disease is prevent in 1 patient

number needed to harm (NNH)

• # of pts who need to be treated for a certain period of time in order for 1 patient to be harmed

• calculated same as NNT, but always round down

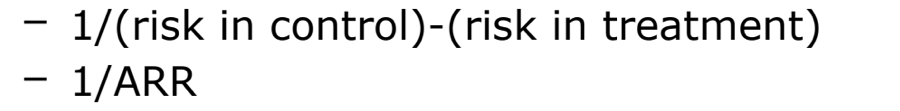
number needed to treat

number needed to harm

• NOT significant means NO clinical interpretation

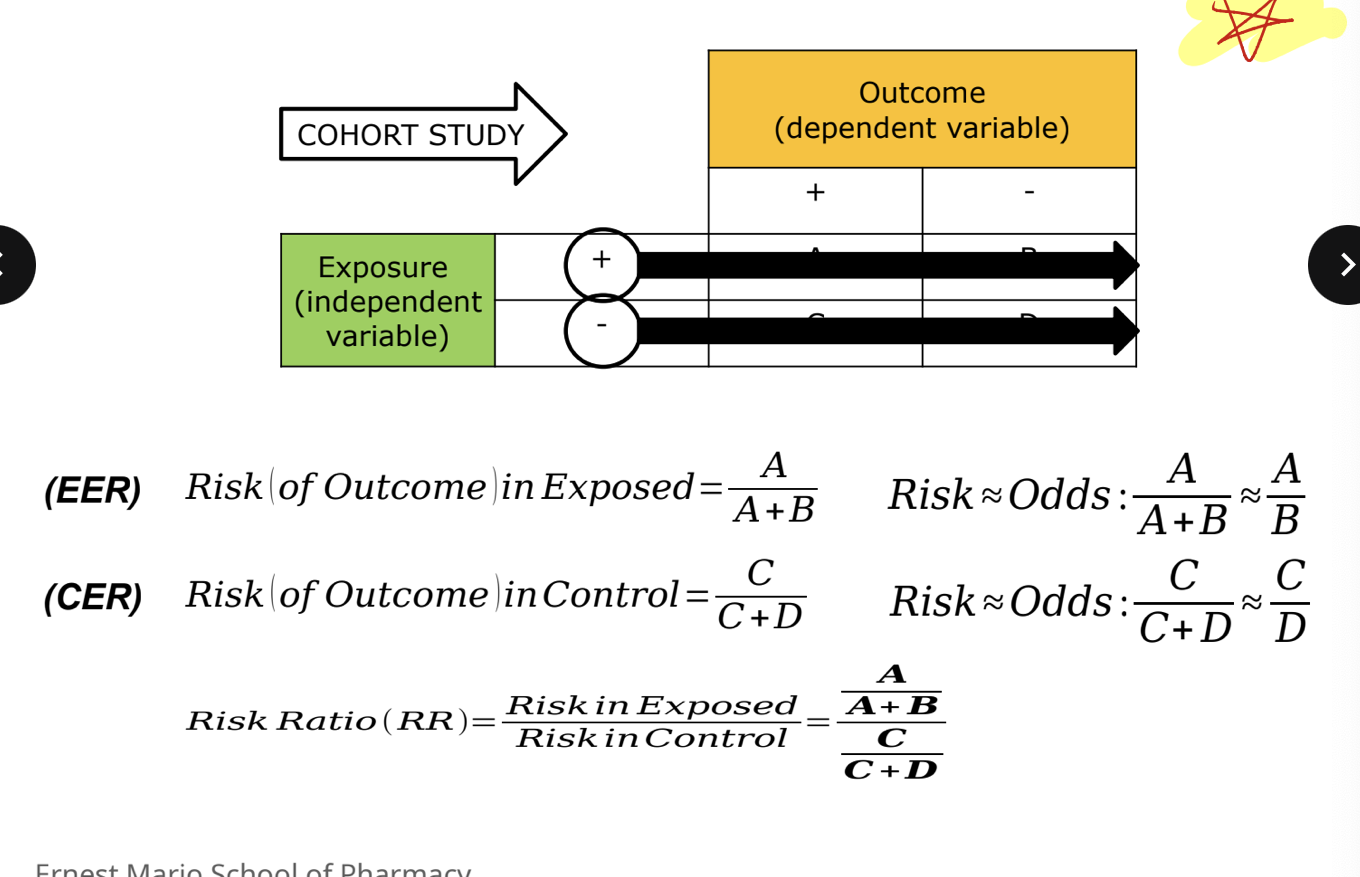
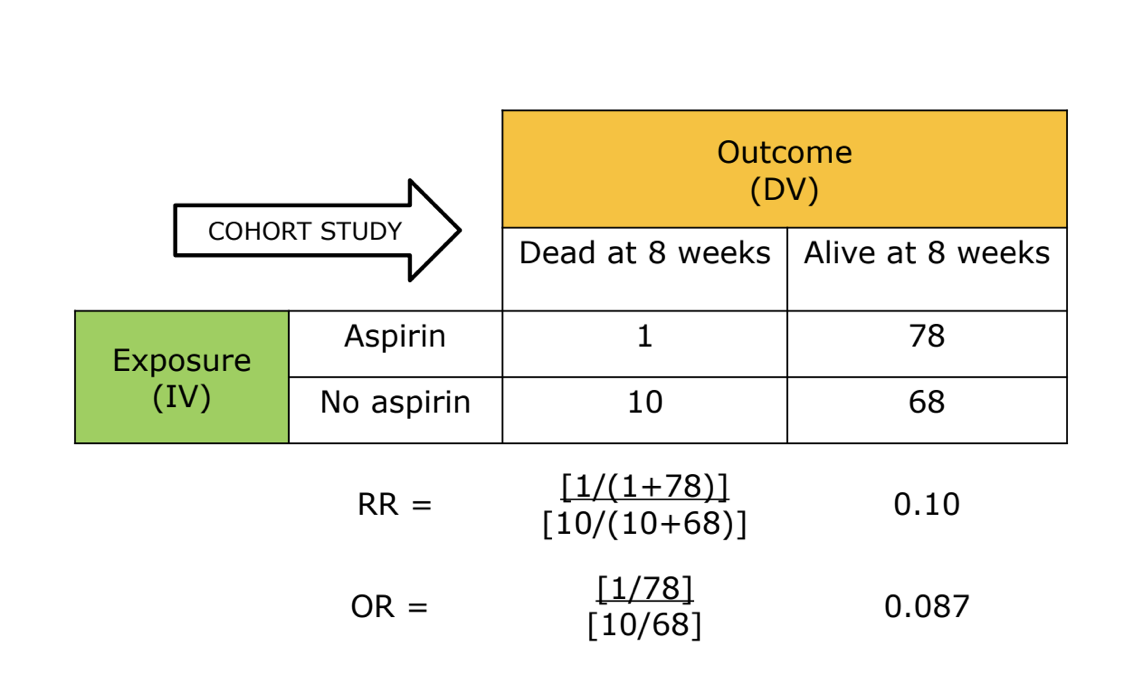
cohort study *

• can be either prospective or retrospective

• starts with exposure and look for outcomes

• can determine a relative risk since we know incidence of an outcome

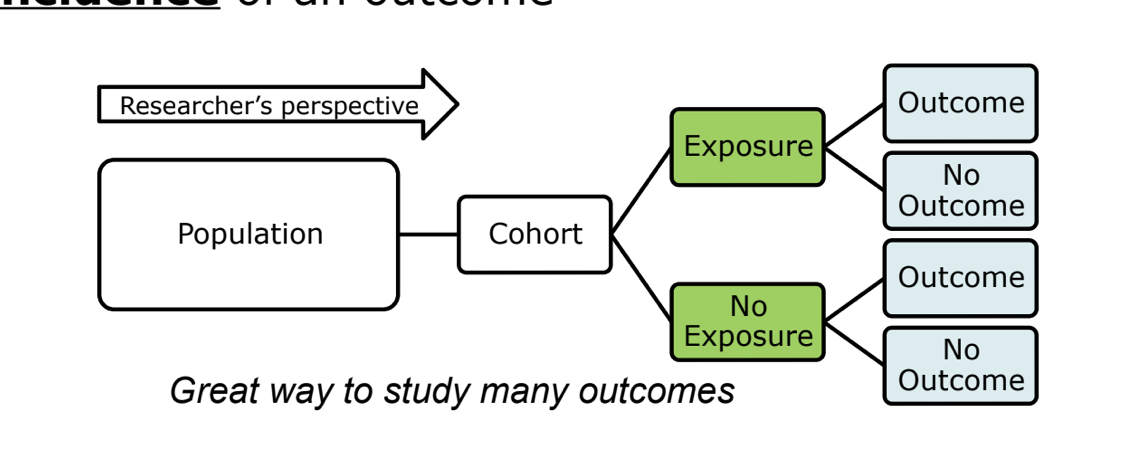
cohort example *

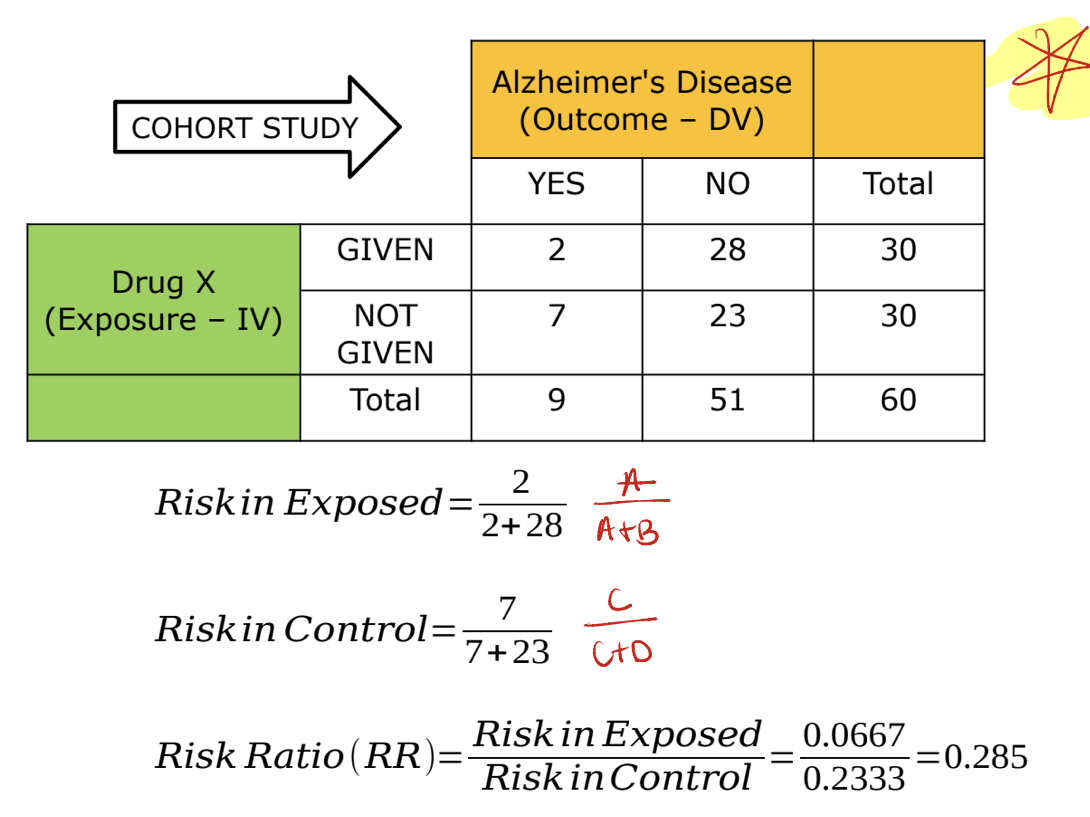
cohort example 2 *

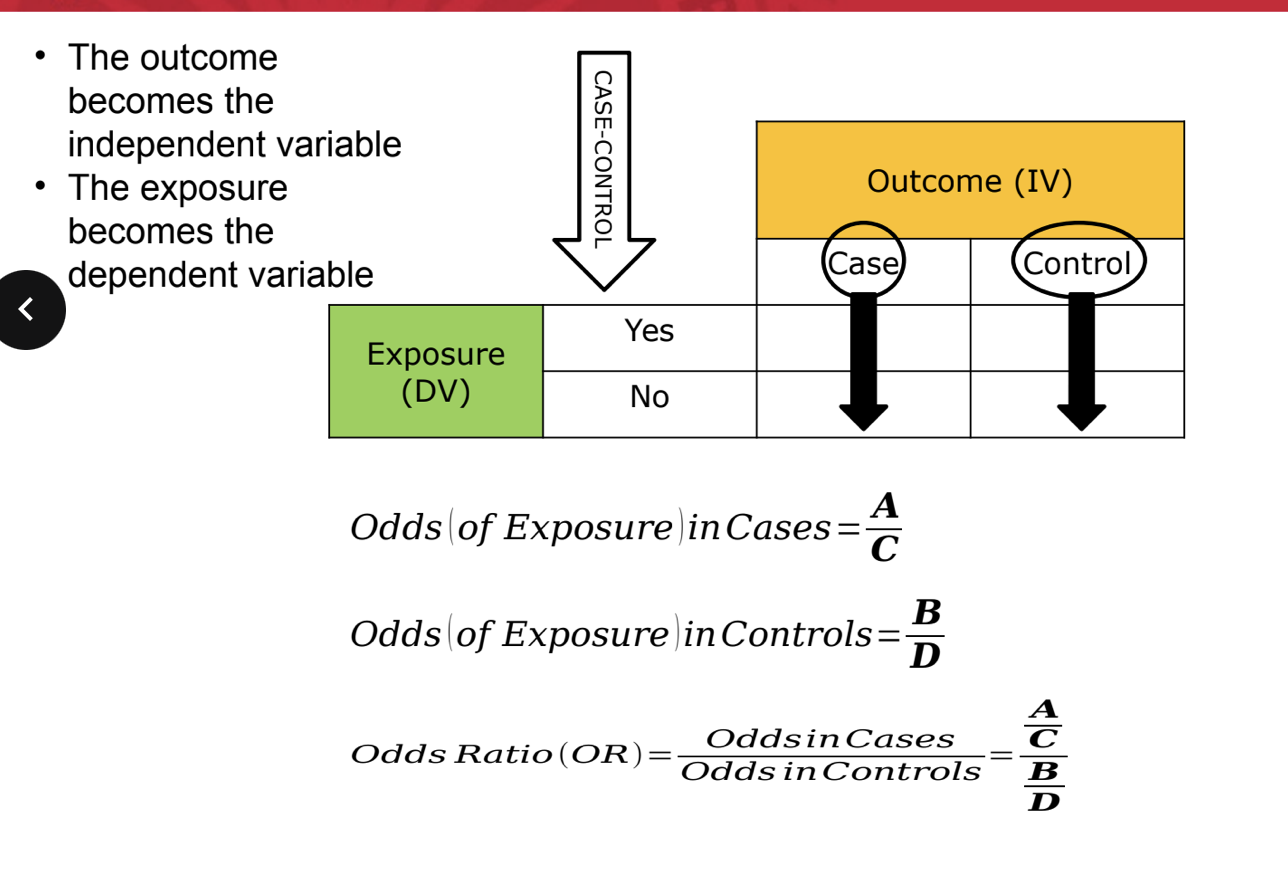
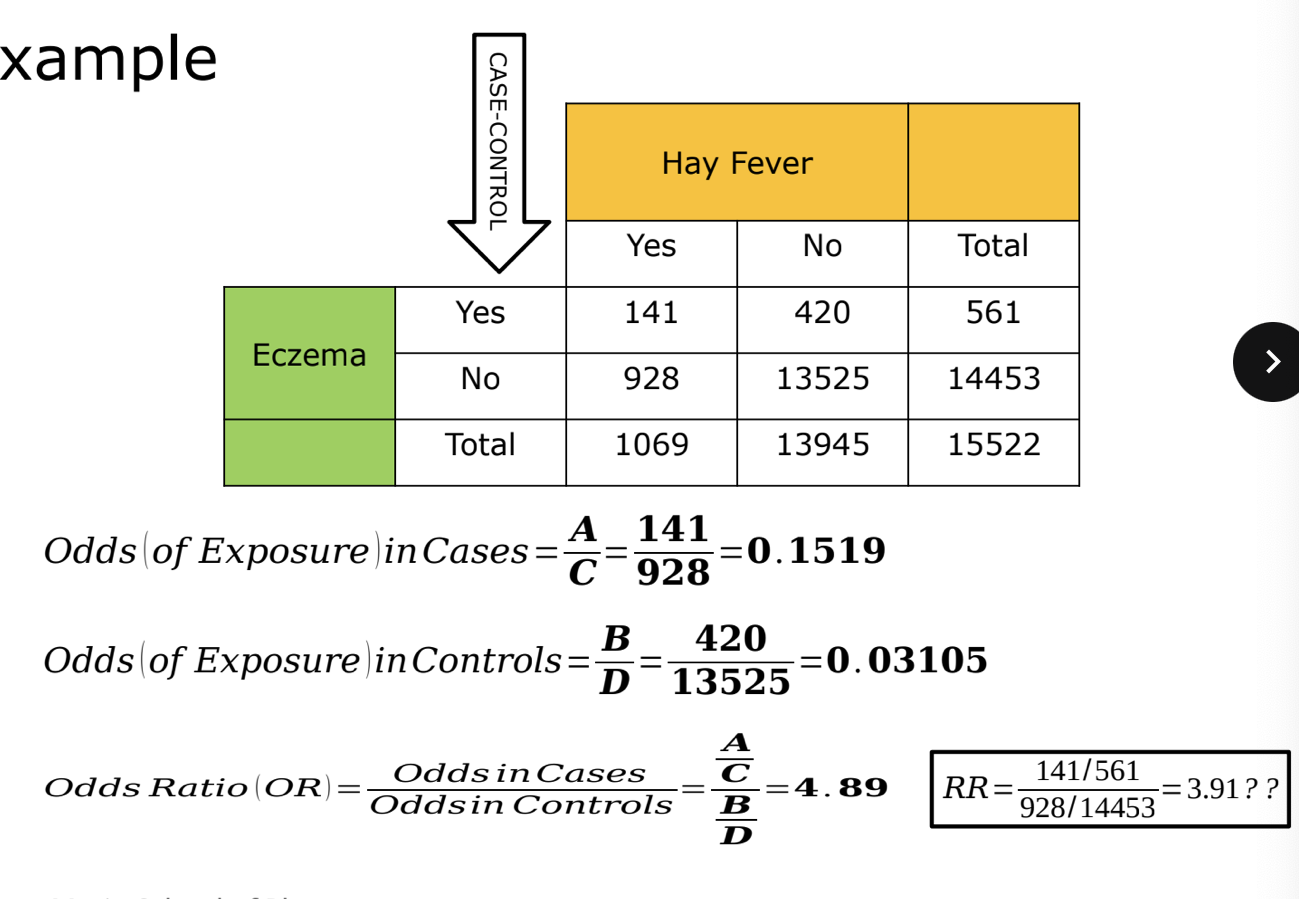
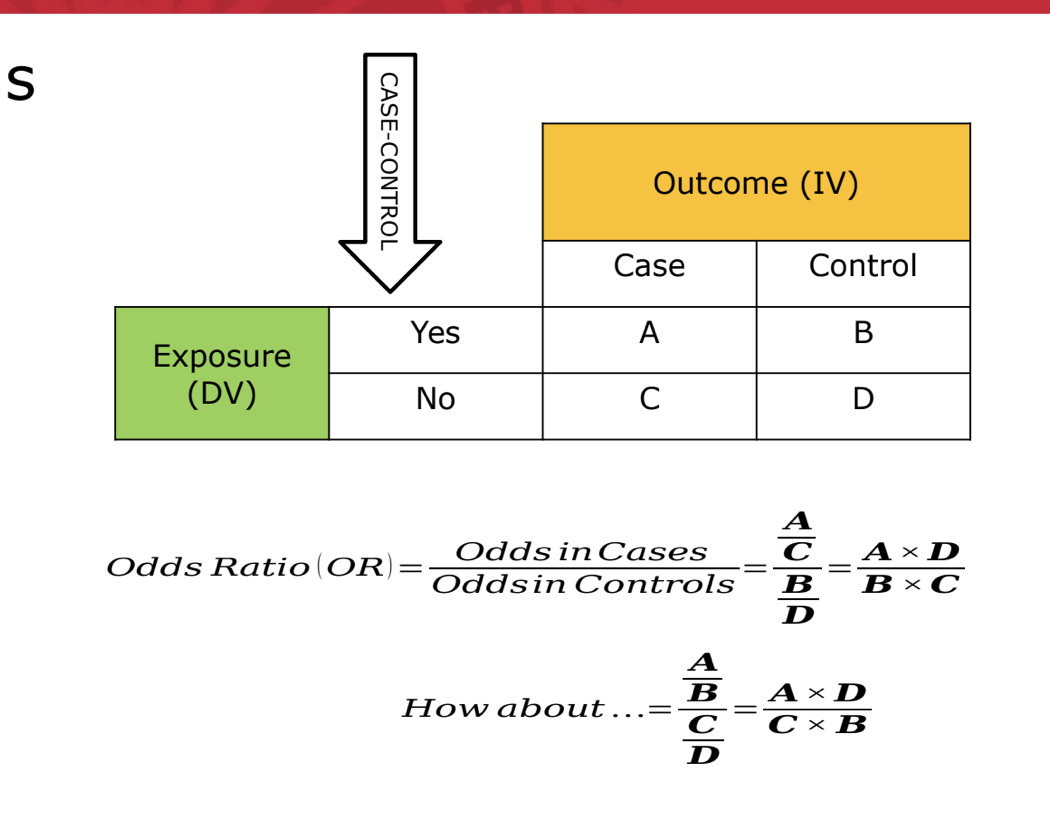
case control

case control example

bonus

more about cohort *

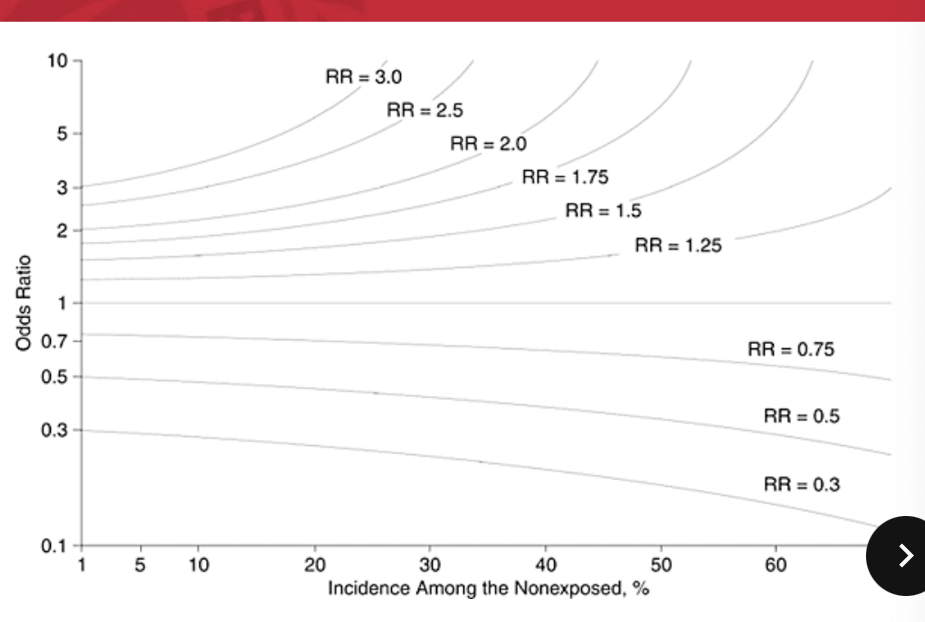
1. when an outcome (DV) is very rare, the OR and RR can be similar, thus we can approximate RR using the OR

2. when an outcome (DV) is common, the OR will overestimate effect thus we need to use RR instead

3. in case control, we do NOT know incidence (specifically, population @ risk) so we have to use odds instead

RR vs OR

• OR can approximate RR but only at low prevalence (<10%)

• higher event prevalence will result in widely exaggerated ORsi

interpreting the OR and RR

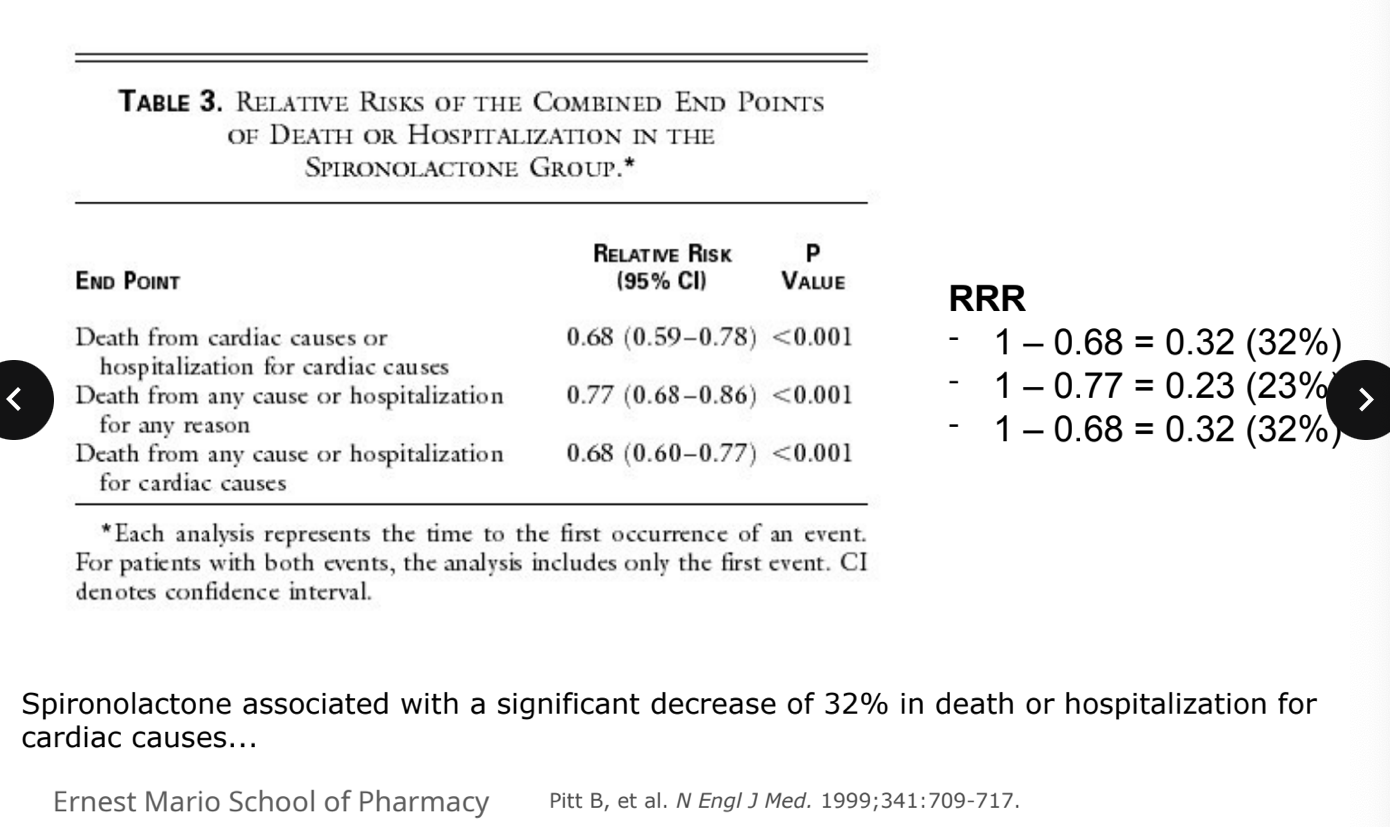
example: RALES trial

spironolactone associated with a sigificant decrease of 32% in death or hospitalization for cardiac causes

survival analysis *

• can be used to analyze a variety of outcomes, including survival or occurent of events such as time to acute MI, onset of cancer, time to discharge

• conventional methods CANNOT be used

  • to compare “mean” or “median” survival times you have to wait until the required # of patients actually die

• allows investigator to incorporate contributions of patients who drop out of the study

survival analysis pt 2

acturial method for survival analysis

• takes fixed time periods and sees who survives to that end point

kaplan-meier

• looks at actual length of time measured for end point

• considered superior to the acturial method esp when N<50

cox’s proprotional hazards model

• used when concerned about group differences at baseline that relate to a covariate that is measured on a continuous scale

• look at survival data and adjust for differences in groups

• controls by confounding issues or by showing differences in survival by baseline characteristics

• concerns with studying the time between study entry and an outcome event

• survival analysis is applicable to any nominal outcome

• typical construct a kaplan-meier curve and then perform a log-rank test to test the significance

• may also perform cox-proportional hazards analysis allowing you to control for confounding and calculate a hazards ratio

  • hazard refers to the chances of an event/outcome to occur within a unit of time assuming that the subject has survived up to that time

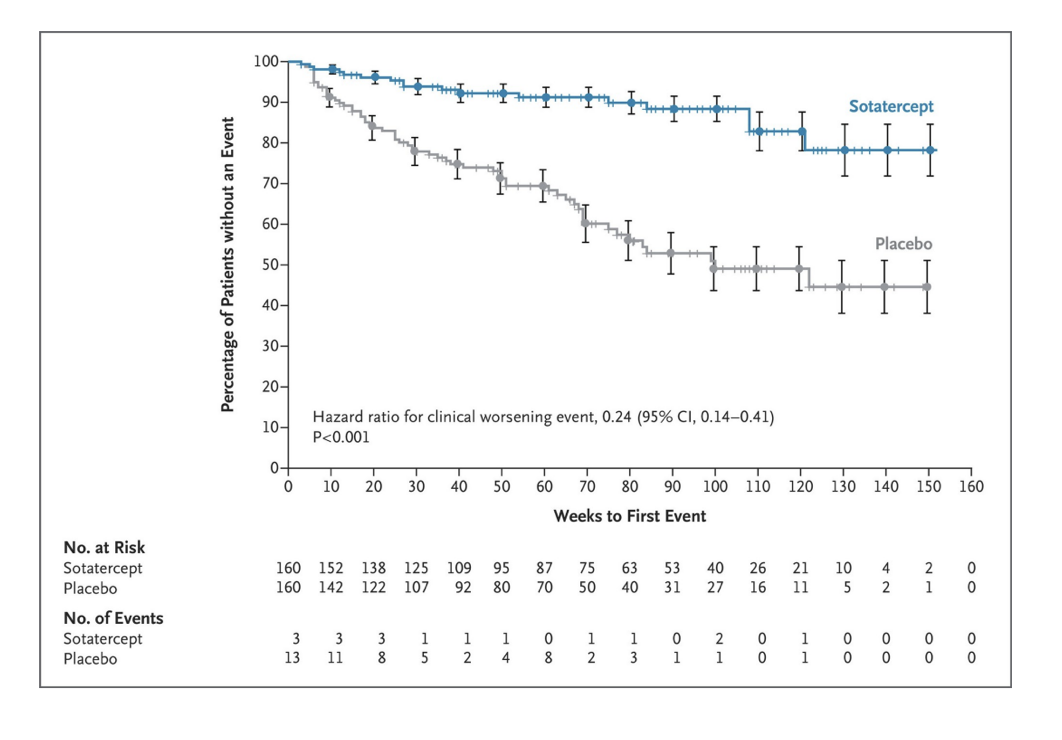
hazards ratio

• interpretation exactly the same as OR or RR

• consider the relative risk increase or decrease associated with this ratio

• must meet certain assumptions for proportional hazards model

  • proportional hazards = same hazards across continuum

example: kaplan-meier plot + hazards ratio

conclusion

• choosing appropriate statistics is essential

• correct presentation of study results ensures transparency

• interpretation enables the translation of study results to clinical practice