topic 5 - forces

state the symbol equation to find momentum

p (kgm/s) = m (kg) x v (m/s)

state conservation of momentum definition

• in a closed system

• the total momentum before an event

• is equal to the total momentum after the event

• therefore energy is conserved

state an example of momentum in an event

collision

state what elastic collision is

• when objects collide

• and move in opposite directions

state what inelastic collision is

• when objects collide

• and move in the same direction

state what happens to kinetic energy in an elastic collision

kinetic energy is conserved

state what happens to kinetic energy in an inelastic collision

• kinetic energy is not conserved

• and it is wasted as heat energy

state what happens to mass and velocity of multiple objects in an elastic collison

the mass and velocity combine

state what happens to momentum in a collision

momentum is always conserved in a collision

explain how to complete calculations of a collision

• write down the known mass and/or velocity of both objects

• use these to calculate the momentum of one of the objects

• the momentum will be the same before and after the event

• use the equation p = m x v to find any unknown data

state what causes a change in momentum

• when a force acts on an object

• that is moving

• or able to move

state the symbol equation to find force using mass and acceleration

F (N) = m (kg) x a (m/s²)

state the symbol equation to find acceleration

a (m/s²) = Δv (m/s) / t (s)

state the equation to find force using velocity, mass and time

F = (m x Δv) / t

state the definition of force

rate of change of momentum

explain how air bags/seat belts work as safety features

• air bags/seat belts absorb energy from collision by changing shape

• for a given force upon impact, the air bags/seat belts absorb energy

• and slows down the rate of change of momentum observed by the passenger as the vehicle comes to rest

• the increased time reduces the force and thus the risk of injury to the passenger

explain why air bags are useful as safety features

• they act as a soft cushion to prevent injury on the passenger

• when they are thrown forward upon impact

explain why seat belts are useful safety features

• they are designed to stop a passenger from colliding with the interior of a vehicle

• by keeping them fixed to their seat in an abrupt stop

• they are designed to stretch slightly

• to increase the time for the passenger’s momentum to reach zero

• and therefore reduce the force of the collision on the passenger

explain how gymnasium crash mats work as safety features

• when an object lands on the crash mat with a large force

• the soft landing means the object is in contact with the mat for a longer period of time

• than if the mat was not there

• this increases the contact time over which their momentum is reduced

• creating a smaller impact force and a lower chance of injury

explain how cycle helmets work as safety features

• when a cyclist’s helmet collides with a surface

• the foam inside the helmet compresses upon impact

• absorbing some of the energy during collision

• slowing down the rate of change of momentum

• this reduction in the rate of change of momentum leads to a decrease in the force experienced by the cyclist’s head

• thus providing protection in case of collision

explain how cushioned areas in playgrounds work as safety features

• when a child falls in the playground

• the cushioned surface reduces the risk of severe injury by increasing the contact time of the child

• which decreases the rate of change of momentum

• decreasing the force

• the mat will be thinner than crash mats as children have a lower mass than adults

explain how increasing contact time in a collision protects passengers

• causes rate of change of momentum to decrease

• causes passenger to experience a smaller force

• decreasing risk of injury

explain how increasing contact time in a plane landing is more comfortable for passengers

• rate of change of momentum is slower

• decreases force experienced by passengers

explain why some planes need longer runways to land safely

• some planes have a larger mass

• causing the aircraft to have more kinetic energy

• due to it having more momentum

state what a scalar quantity is

quantity with magnitude

state what a vector quantity is

quantity with magnitude and direction

state the definition of a force

the rate of change of momentum

state the definition of a contact force

when a force is exerted when objects are physically-touching

state the definition of a non-contact force

when a force is exerted when objects are physically-separated

state examples of contact forces

• friction

• air resistance

• tension

• normal contact force

state examples of non-contact forces

• gravitational force

• electrostatic force

• magnetic force

state what kind of quantity force is

vector

state what kind of force weight is

• force acting on an object

• due to gravity

state what causes the force of gravity close to earth

gravitational field strength around the earth

state what influences the weight of an object

• gravitational field strength

• of the area where the object is located

state word equation to calculate weight

weight = mass x gravity

state symbol equation to calculate weight

w = m x g

state where the weight of an object acts

• single point

• referred to as

• the centre of mass

state the relationship between the weight and mass of an object

directly proportional

state how weight is measured

using a calibrated spring balance (newton meter)

state what a resultant force is

the sum of all forces acting on an object

state what causes work to be done

• a force causing an object

• to move through a distance

state when a force does work on an object

• when the force causes

• a displacement of the object

state word equation to calculate work done

work done = force x distance

state symbol equation to calculate work done

wd (J) = F (N) x s (m)

state what causes one joule of work to be done

• when a force of one newton

• causes a displacement

• of one metre

state numerical relationship between joules and newton-metres

1 joule = 1 newton-metre

state what occurs when work is done against frictional forces acting on an object

temperature rise in the object

state forces involved in stretching an object

• requires two forces

• acting away from each other

state forces involved in compressing an object

• requires two forces

• acting towards each other

state forces involved in bending an object

• requires two forces

• acting towards each other

• at different points on the object

• or two forces at an angle to each other

explain why changing the shape of an object requires more than one force

• because a single force applied would cause

• the object to move in the direction

• that force applied

deformation definition

change of shape

state when elastic deformation occurs

• objects return to original shape

• when stretching force is removed

state when inelastic deformation occurs

• object remains stretched

• and doesn’t return to completely to original shape

• when stretching force is removed

state the relationship between the extension of an elastic object and the force applied

directly proportional

state Hooke’s law equation (word)

force = spring constant x extension

state Hooke’s law equation (symbol)

F (N) = k (N/m) x e (m)

state what happens when a force stretches/compresses an object

work is done

state where energy is stored when an object is stretched/compressed

• elastic potential store

• of the spring

state the numerical relationship between force and energy on a stretched/compressed object

• work done and energy stored

• in elastic potential store of the spring

• is equal

state what changes the numerical relationship between force and energy on a stretched/compressed object

if the object is inelastically deformed

state what Hooke’s law is

linear relationship between force and extension

describe the difference between linear and non-linear relationships between force and extension

• linear relationships on a force-extension graph

• connote materials that obey Hooke’s law

• portrayed by a straight line

• non-linear relationships on a force-extension graph

• connote materials that do not obey Hooke’s law

• portrayed by a curve

explain how to calculate spring constant from a linear force-extension graph

• rearrange Hooke’s law equation to find spring constant

• calculate the change in force divided by the change in extension

• a steep gradient means the material has a small spring constant

• a shallow gradient means the material has a large spring constant

state symbol equation to calculate work done in stretching/compressing a spring

E_e (J) = 0.5 x k (N/m) x e² (m)

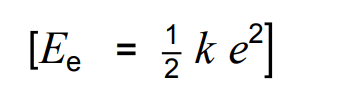
state the variables in the investigation of force and extension

• independent = force

• dependent = extension

• control = spring constant

state method to investigate force and extension

1. set up a clamp and stand, with a vertical ruler, spring and a pointer

2. align the pointer to a value on the ruler and record the initial length of the spring

3. add a 100g mass hanger to the spring

4. record the mass in kg and position of the pointer on the ruler in cm once the spring has extended

5. add a 100g to the mass hanger

6. record the new mass and position of the pointer on the ruler

7. repeat the process another 4 times

8. remove all the masses (including the mass hanger) and repeat the experiment three times

9. calculate the average length of the spring from your repeated experiments

analyse the results of the investigation of force and extension

• force added to the spring is the weight of the masses

• weight is calculated using equation: w = m x g

• extension of the spring is calculated using equation: final length - original length

• plot a graph of force (y-axis) against extension (x-axis)

• draw a line of best fit

• if the graph is linear, the spring obeys Hooke’s law

evaluate the investigation of force and extension

• record readings from the ruler at eye level

• to avoid parallax error

• use a pointer to improve accuracy of ruler readings

• to avoid random error

• wait a few seconds for the spring to fully extend when mass is added

• before taking the new reading length

state what causes an object to rotate

force or system of forces

state examples of rotation

• person on see-saw

• turning handle of a spanner

• door opening and closing

state moment of force definition

turning effect of a force

state moment of force word equation

moment of force (Nm) = force (N) x distance (m)

state what happens to moments if an object is balanced

• total anti-clockwise moment around a pivot

• is equal

• to the total clockwise moment around a pivot

state methods to transmit rotational effects of forces

• simple lever

• simple gear system

explain how levers transmit the rotational effects of forces

• levers increase the size of the force

• acting on an object

• to make the object turn more easily

• force applied to a lever must act further from the pivot

• than the force has to overcome

state how to make a lever work better

• increase size of the force applied

• increase distance of force from pivot

explain how gear systems transmit the rotational effects of forces

• gears multiply the effect of a turning force using moments

• they consist of wheels with toothed edges

• that rotate on an axle, which acts as a pivot

• as one gear turns, the other must also turn

• where gears meet, the teeth will move in the same direction

• one of the gears will move clockwise

• the other gear will move anti-clockwise

state what influences the moment of a gear in a simple gear system

• the moment depends on the size of the gear

• which changes the distance of the teeth to the pivot

state what increases the moment of a gear

• when it’s driven by a smaller gear

• where the larger gear will rotate slower

• than the smaller gear

• but will have a greater moment

state what decreases the moment of a gear

• when it’s driven by a larger gear

• where the smaller gear will rotate quicker

• than the larger gear

• but will have a smaller moment

state what physical state a fluid can be

liquid or gas

state what pressure in fluid causes

force normal to any surface

state what a force acting normal means

force is acting at right angles

state symbol equation to calculate pressure at surface of a fluid

p (Pa) = F (N) / A (m²)

state word equation to calculate pressure at surface of a fluid

pressure = force / area

state word equation to calculate pressure due to a column of liquid

pressure = height x density x gravitational field strength

explain why pressure at a point in a liquid increases with the height of the water above that point

• more liquid is above the point, causing pressure on the point to increase

• as the excess pressure is caused by the increased weight of the liquid

• pushing against objects immersed in the liquid

state where a submerged object experiences a larger pressure in a liquid

bottom surface of the liquid

state what resultant force pressure on a submerged object causes

upthrust

describe factors that influence floating

• if upthrust on an object

• is equal to or greater than

• the object’s weight

• or if the density of the object

• is less than

• the density of the fluid

describe factors that influence sinking

• if upthrust on an object

• is less than

• the object’s weight

• or if the density of the object

• is more than

• the density of the fluid

state what the atmosphere is

• thin layer

• of air

• around the earth

state how altitude affects the density of the atmosphere

• increasing altitude

• decreases density

• of the atmosphere

state what causes atmospheric pressure

• air molecules

• colliding with a surface

state what happens to the number of air molecules above a surface as altitude increases

decreases

state what happens to atmospheric pressure when altitude increases

decreases

state the numerical value of atmospheric pressure

100,000 Pa

state distance definition

how far an object moves