dynamics test 3

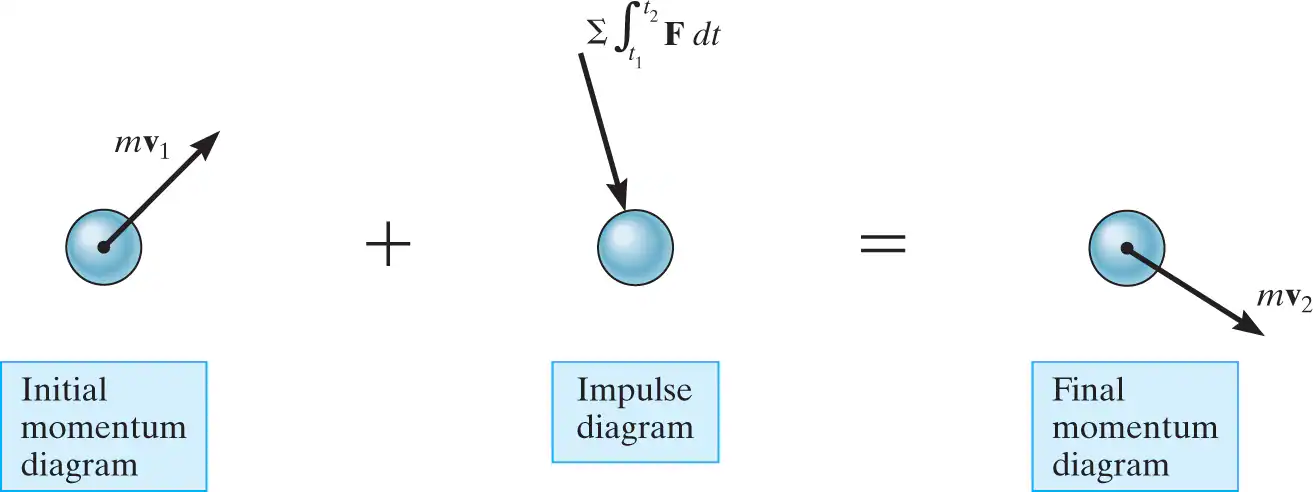
principle of linear impulse and momentum equation

sum of integral from t1 to t2 of Fdt= mv2-mv1

provides a direct means of obtaining the particle’s final velocity v2 after a specified time period when the particle’s initial velocity is known and the forces acting on the particle are either constant or can be expressed as functions of time.

linear momentum vector direction and units

Since the particle’s mass m is a positive scalar, the linear-momentum vector has the same direction as v, and its magnitude has units of mass times velocity

linear impulse

I=integral of Fdt

This term is a vector quantity which measures the effect of a force during the time the force acts

linear impulse direction and units

Since time is a positive scalar, the impulse acts in the same direction as the force, and its magnitude has units of force times time, e.g., N·s or lb·s*

If the force is expressed as a function of time, the impulse can be determined by

evaluation of the integral.

As a special case, if the force is constant in both magnitude and direction, then the impulse becomes

I=∫ from t1 to t2 of Fdt=F(t2-t1)

principle of linear impulse and momentum rewritten for problem solving

mv1+∑ ∫ from t1 to t2 of F dt=mv2

which states that the initial momentum of the particle at time t1 plus the sum of all the impulses applied to the particle from t1 to t2 is equivalent to the final momentum of the particle at time t2.

momentum diagram, impulse diagram, and final momentum diagram

linear momentum (only)

L=mv

If each of the vectors are resolved into its x, y, z components, we can write the following three scalar equations of linear impulse and momentum:

m(vx)1+ sum of S t1 to t2 Fx dt=m(vx)2

do the same for y and z.

to solve linear momentum and impulse problems:

-draw the FBD to account for all forces creating an impulse on a particle

-the direction of the particles initial and final velocities should be established as measured from an inertial reference frame.

-apply the principle of impulse and momentum.

mv1+sum(S from t1 to t2)Fdt= mv2

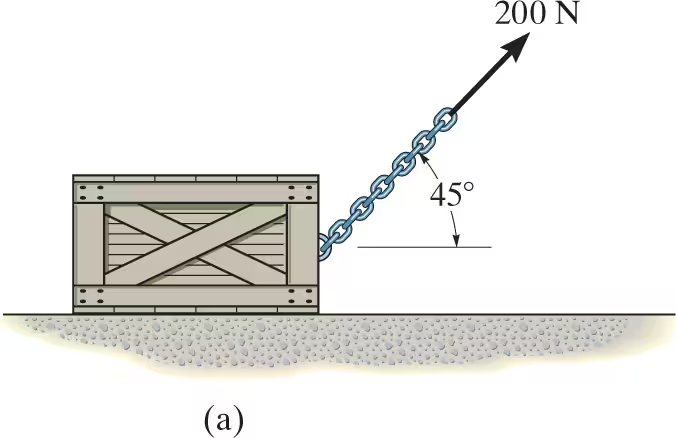
The 100-kg crate shown is originally at rest on the smooth horizontal surface. If a towing force of 200 N, acting at an angle of 45°, is applied for 10 s, determine the final velocity of the crate and the normal force which the surface exerts on the crate during this time interval.

This problem can be solved using the principle of impulse and momentum since it involves force, velocity, and time.

Since all the forces are constant, the impulses are simply the product of the force magnitude and 10 seconds

m(vx)1+sum of S from t1 to t2 (Fxdt)=m(vx)2

= 0+200*cos45×10=100(v2)

vs=14.1m/s

velocities are in x-dir so use force in x-dir to solve for v2.

m(vy)1+sum of S from t1 to t2 (Fydt)=m(vy)2

0+ N(10)-981(10)+200(sin45)(10)= 0

USING ALL Y FORCES!!

N= 840N

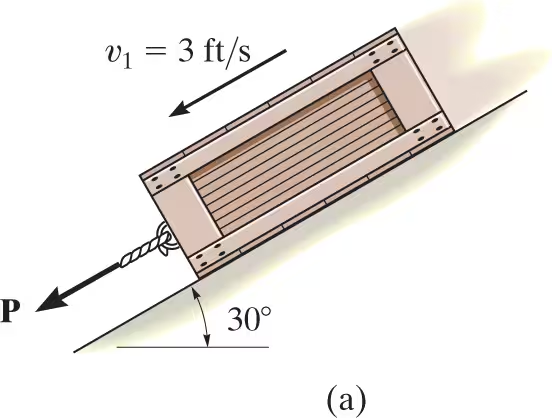
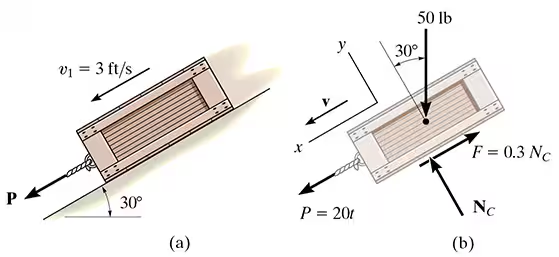
The 50-lb crate shown is acted upon by a force having a variable magnitude  P=20t lb, where t is in seconds. Determine the crate’s velocity when  t=2 s if the initial velocity of the crate is v1=3 ft/s down the plane. The coefficient of kinetic friction between the crate and the plane is μk=0.3.

Since the magnitude of force P=20t varies with time, the impulse it creates must be determined by integrating over the 2-s time interval.

m(vx)1+sum of S from t1 to t2 (Fxdt)=m(vx)2

50/32.2(3)+int(0 to 2)20tdt-.3N(2)+50(sin30)(2)= 50/32.2 v2

this gets 4.658+40-.6N+50=1.553v2

just use Fy=0 to find Nc.

Nc-50cos30=0

Nc=43.3lb

v2=44.2ft/s

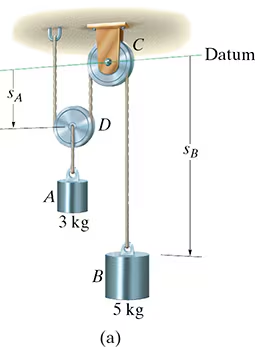
Blocks A and B shown have a mass of 3 kg and 5 kg, respectively. If the system is released from rest, determine the velocity of block B in 6 s. Neglect the mass of the pulleys and cord.

Since the weight of each block is constant, the cord tensions will also be constant. Furthermore, since the mass of pulley D is neglected, the cord tension TA=2TB. Note that the blocks are both assumed to be moving downward in the positive coordinate directions, sA and sB.

Block A:

m(vA)1+sum of S from t1 to t2 (Fydt)=m(vA)2

0-2TB(6)+3(9.81)(6)=3(vA)2

note that for A, the upward tension force will be 2TB

the downward force will be mass*9.81

Block B:

m(vB)1+ sum of S from t1 to t2 (Fydt)= m(vB)2

0+5(9.81)(6)-TB(6)=5(vB)2

note that for B, the upward tension force will be TB

the downward force will be mass*9.81

there are 3 unknowns! there needs to be another equation.

2sA+sB=l

2vA=-vB

these equations yield vB2= 35.8m/s

TB= 19.2N

conservation of linear momentum

When the sum of the external impulses acting on a system of particles is zero, reduces to a simplified form, namely,

∑mivi1=∑mivi2

This equation is referred to as the conservation of linear momentum. It states that the total linear momentum for a system of particles remains constant during the time period t1 to t2.

The conservation of linear momentum is often applied when

particles collide or interact.

impulsive forces

forces which are very large and act for a very short period of time produce a significant change in momentum

nonimpulsive forces

If the time over which the motion is studied is very short, some of the impulses may also be neglected or considered approximately equal to zero. The forces causing these negligible impulses are called nonimpulsive forces

impulsive vs. nonimpulsive forces

Impulsive forces normally occur due to an explosion or the striking of one body against another, whereas nonimpulsive forces may include the weight of a body, the force imparted by a slightly deformed spring having a relatively small stiffness, or for that matter, any force that is very small compared to other larger (impulsive) forces.

When making this distinction between impulsive and nonimpulsive forces, it is important to realize that this only applies during the time t1 to t2.

To illustrate, consider the effect of striking a tennis ball with a racket as shown in the photo on the next page. During the very short time of interaction, the force of the racket on the ball is impulsive since it changes the ball’s momentum drastically. By comparison, the ball’s weight will have a negligible effect on the change in momentum, and therefore it is nonimpulsive

If an impulse–momentum analysis is considered during the much longer time of flight after the racket–ball interaction, then the impulse of the ball’s weight is important since it, along with air resistance, causes the change in the momentum of the ball.

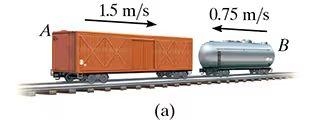
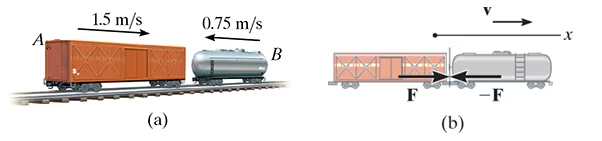
The 15-Mg boxcar A is coasting at  1.5 m/s on the horizontal track when it encounters a 12-Mg tank car B coasting at  0.75 m/s toward it as shown. If the cars collide and couple together, determine (a) the speed of both cars just after the coupling, and (b) the average force between them if the coupling takes place in 0.8 s.

We use conservation of linear momentum because:

1. No external horizontal forces act on the system (friction and air resistance are negligible).

2. Momentum is always conserved in a collision, whether elastic or inelastic.

3. The problem involves a completely inelastic collision (the cars couple together), meaning kinetic energy is not conserved, but momentum still is.

a.

As shown, we have considered both cars as a single system. By inspection, momentum is conserved in the x direction since the coupling force F is internal to the system and will therefore cancel out. It is assumed that when coupled, both cars move at v2 in the positive x direction.

conservation of linear momentum:

mA(vA)1+mB(vB)1=(mA+mB)v2

(15000)(1.5m/s)-12000(.75)=27000v2

v2=.5m/s

b.

The average (impulsive) coupling force, Favg, can be determined by applying the principle of linear momentum to either one of the cars.

using car 2 with v to the right and -F to the left,

mA(vA)1+sum of SFdt= mAv2

15000(1.5)-Favg(.8)=15000(.5)

Favg= 18.8kN

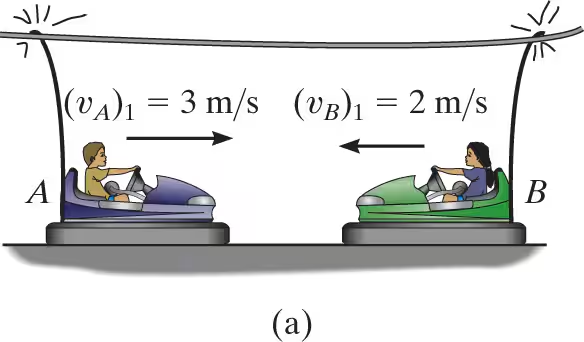
The bumper cars A and B each have a mass of 150 kg and are coasting with the velocities shown before they freely collide head on. If no energy is lost during the collision, determine their velocities after collision.

To determine the velocities of bumper cars A and B after a perfectly elastic head-on collision, we use:

1. Conservation of Linear Momentum – Because no external forces act on the system, total momentum before and after the collision remains constant.

2. Conservation of Kinetic Energy – Since the collision is elastic, no mechanical energy is lost.

The cars will be considered as a single system. The free-body diagram is shown

conservation of momentum: SINCE THEY ARE COLLIDING

mA(vA)1+mB(vB)1= mA(vA)2 + mB(vB)2

150×3+150*-2=150*vA2+150*vB2

vA2= 1-vB2

Since no energy is lost, the conservation of energy theorem gives

T1+V1=T2+V2

1/2mA(vA)1²+1/2mB(vB)1²+0=1/2mA(vA)2²+1/2mB(vB)2²+0

1/2(150)(3)²+1/2(150)(2)²+0=1/2(150)(vA)2²+1/2(150)(vB)2²+0

(vA)2²+(vB)2²=13

aolcing, you get vB2=3m/s and VA2=2m/s

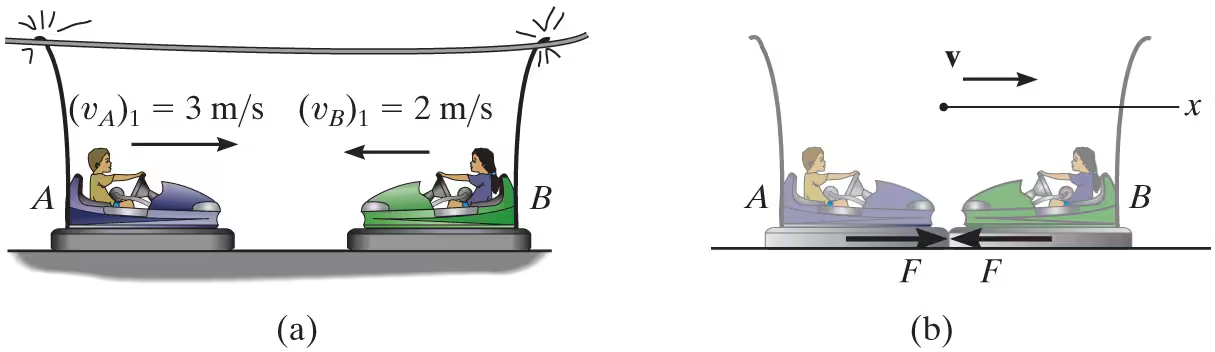
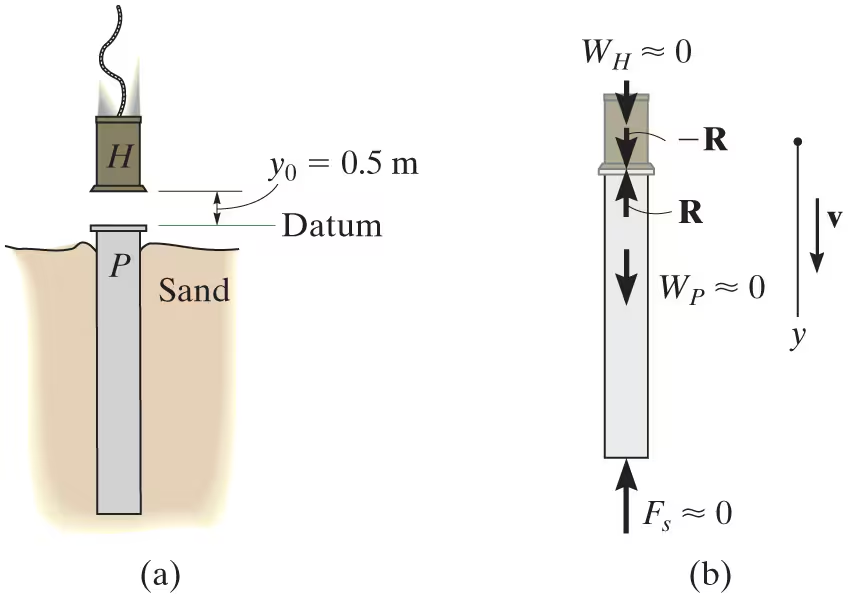
An 800-kg rigid pile P shown is driven into the ground using a 300-kg hammer. The hammer falls from rest at a height  y0=0.5 m and strikes the top of the pile. Determine the impulse which the pile exerts on the hammer if the pile is surrounded entirely by loose sand, so that after striking, the hammer does not rebound off the pile.

• Conservation of Linear Momentum is used because:

  • The hammer and pile system experiences no external horizontal forces.

  • The hammer and pile form a single system upon impact (perfectly inelastic collision).

  • This allows us to find the velocity immediately after impact.

• Impulse-Momentum Principle is used because:

  • The hammer experiences a change in momentum due to the force exerted by the pile.

  • Impulse relates this force to the change in momentum, helping determine the impulse exerted by the pile.

The velocity at which the hammer strikes the pile can be determined using the conservation of energy equation applied to the hammer. With the datum at the top of the pile, we have

T0+V0=T1+V1

1/2mH(vH)0²+WHy0 = 1/2mH(vH)1²+WHy1

0+300(9.81)(.5)=1/2(300)(vH)1²+0

vH1=3.132m/s

From the physical aspects of the problem, the free-body diagram of the hammer and pile, indicates that during the short time from just before to just after the collision, the weights of the hammer and pile and the resistance force Fs of the sand are all nonimpulsive. The impulsive force R is internal to the system and therefore cancels. Consequently, momentum is conserved in the vertical direction during this short time.

Conservation of momentum:

Since the hammer does not rebound off the pile just after collision, then vH2=vP2=v2.

mH(vH)1+mP(vP)1=mHv2+mPv2

300(3.132)+0=300v2+800v2

v2=.8542m/s

principle of impulse and momentum:

mH(vH)1+sum of S from t1 to t2 of Fydt= mHv2

300(3.132)-SRdt= 300(.8542)

SRdt=683N*s

how to know when to solve problems using principle of impulse and momentum

Principle of Impulse and Momentum:

Use When:
✅ A force acts over a time interval and affects motion.
✅ You need to determine force, impulse, or velocity after an impact.
✅ The problem involves a sudden interaction, such as collisions or external forces.

how to know when to solve problems using conservation of linear momentum

Conservation of linear momentum:

Use When:
✅ No external forces (or they cancel out) act on the system.
✅ A collision or interaction occurs between two or more objects.
✅ The problem asks for velocities before or after a collision.

how to know when to solve problems using principle of impulse and momentum, conservation of momentum, or conservation of kinetic energy

Conservation of kinetic energy:

Use When:
✅ The problem involves elastic collisions (where kinetic energy is conserved).
✅ You need to determine final velocities in perfectly elastic collisions.
✅ No external work is done on the system (no energy loss).

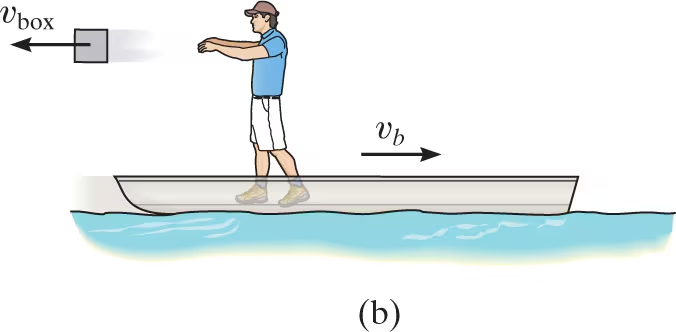
The 80-kg man can throw the 20-kg box horizontally at 4 m/s when standing on the ground. If instead he firmly stands in the 120-kg boat and throws the box, as shown in the photo, determine how far the boat will move in three seconds. Neglect water resistance.

If the man, boat, and box are considered as a single system, the horizontal forces between the man and the boat and the man and the box become internal to the system, and so linear momentum will be conserved along the x axis.

When writing the conservation of momentum equation, it is important that the velocities be measured from the same inertial coordinate system, assumed here to be fixed. From this coordinate system, we will assume that the boat and man go to the right while the box goes to the left

0+0+0= (mm+mb)vb-mboxvbox

0=(80+120)vb-20vbox

vbox=10vb

Since the velocity of the box relative to the man (and boat), vbox/b, is known, then vb can also be related to vbox using the relative velocity equation.

vbox=vb+vbox/b

-vbox=vb-4m/s

solving,

vbox=3.64m/s

vb=.3636m/s

The displacement of the boat in three seconds is therefore

sb=vbt=.3636(3)=1.09m

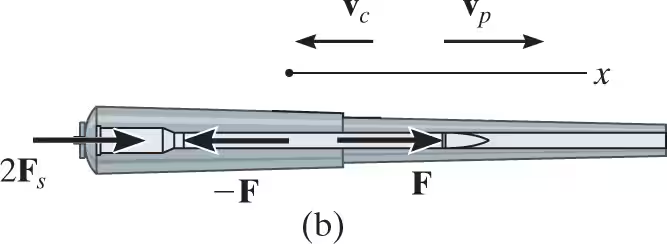
The 1200-lb cannon shown fires an 8-lb projectile with a muzzle velocity of  1500 ft/s measured relative to the cannon. If firing takes place in 0.03 s, determine the recoil velocity of the cannon just after firing. The cannon support is fixed to the ground, and the horizontal recoil of the cannon is absorbed by two springs.

• Conservation of Momentum: This principle establishes a relationship between the recoil velocity of the cannon (vc)2(v_c)_2(vc​)2​ and the projectile's velocity (vp)2(v_p)_2(vp​)2​ as observed from the ground.​

• Kinematic Equation for Relative Velocity: The equation (vp)2=(vc)2+(vp/c)2 relates the projectile's velocity relative to the ground to its velocity relative to the cannon and the cannon's recoil velocity. Given that (vp/c​)2​=1500 ft/s (the muzzle velocity relative to the cannon), we can substitute this into the equation.​

• Solving the System: With these two equations, we have a system that can be solved simultaneously to find the values (vp​)2​.

mc*(vc)1+mp(vp)1=-mc(vc)2+mp(vp)2

0+0=-1200/32.2(vc)2+8/32.2(vp)2

(vp)2=150(vc)2

These two unknown velocities are measured by a fixed observer. As in Example 15.7, they can also be related using the relative velocity equation.

(vp)2=(vc)2+(vp/c)2

(vp)2=−(vc)2+1500ft/s

(vc)2=9.93ft/s

(vp)2=1490ft/s

impact

Impact occurs when two bodies collide with each other during a very short period of time, causing relatively large (impulsive) forces to be exerted between the bodies. The striking of a hammer on a nail, or a golf club on a ball, are common examples of impact loadings.

central impact vs. oblique impact

Central impact occurs when the direction of motion of the mass centers of the two colliding particles is along the line of impact that passes through the mass centers of the particles. This line is perpendicular to the plane of contact, as shown. When the motion of one or both of the particles makes an angle with the line of impact the impact is said to be oblique impact.

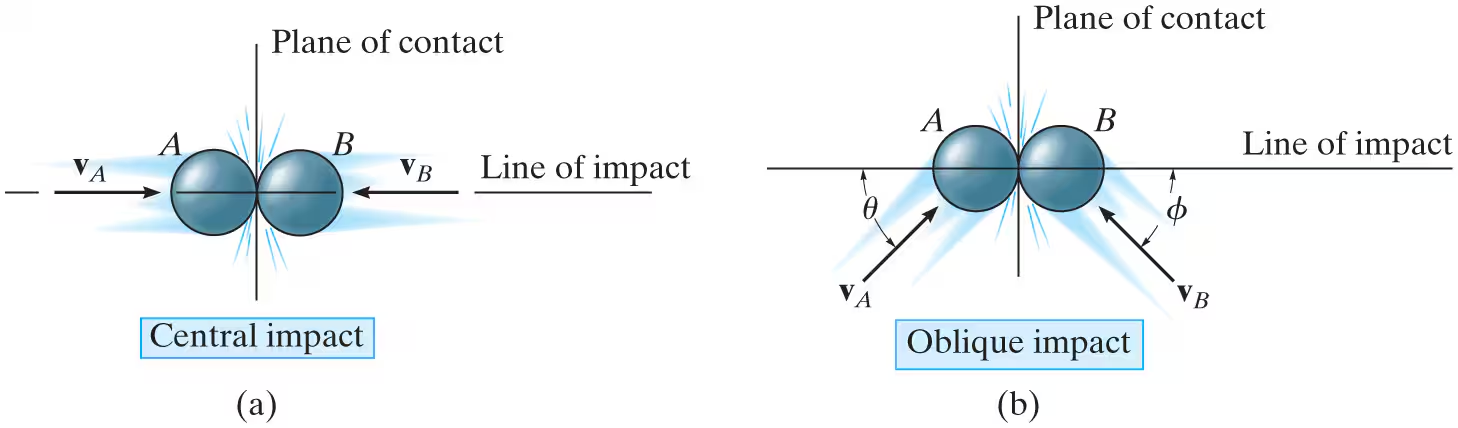
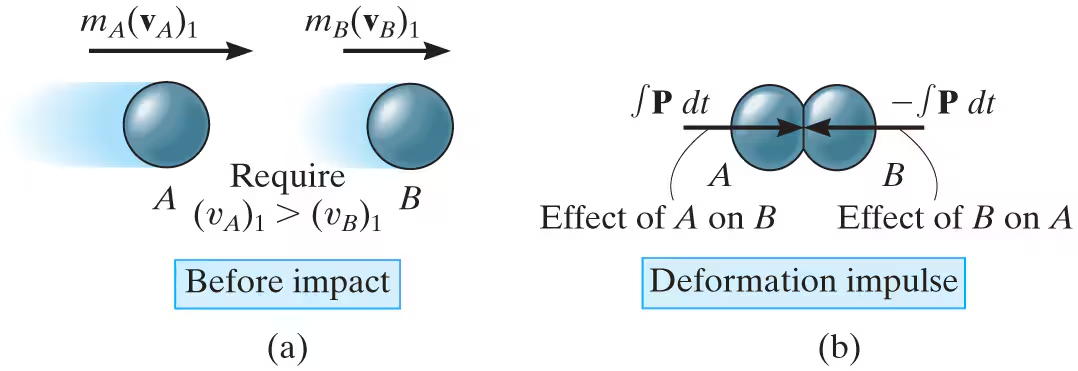
central impact diagrams: before impact

The particles have the initial momenta shown. Provided vA1>vB1, collision will eventually occur.

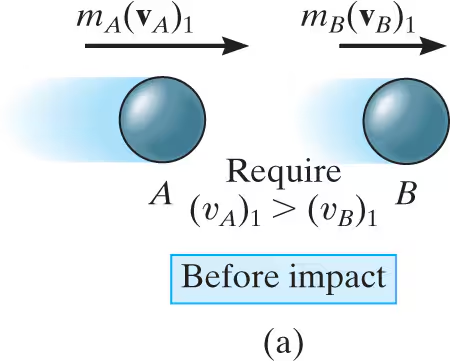
central impact diagrams: deformation impulse

During the collision the particles must be thought of as deformable or nonrigid. The particles will undergo a period of deformation such that they exert an equal but opposite deformation impulse  ∫P dt on each other

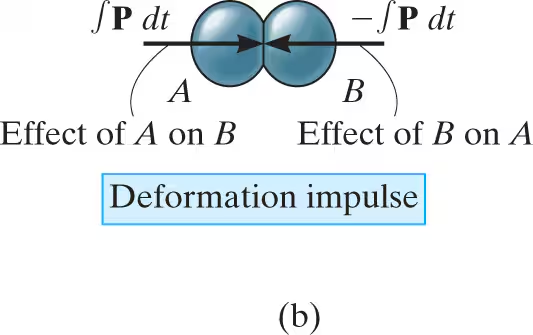
central impact diagrams: maximum deformation

Only at the instant of maximum deformation will both particles move with a common velocity v, since their relative motion is zero

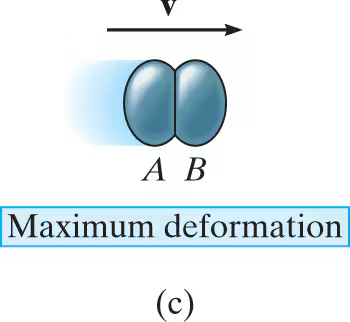
central impact diagrams: restitution impulse

Afterward a period of restitution occurs, in which case the particles will either return to their original shape or remain permanently deformed. The equal but opposite restitution impulse  ∫R dt pushes the particles apart from one another. In reality, the physical properties of any two bodies are such that the deformation impulse will always be greater than the restitution impulse, i.e.,   ∫P dt>∫R dt.

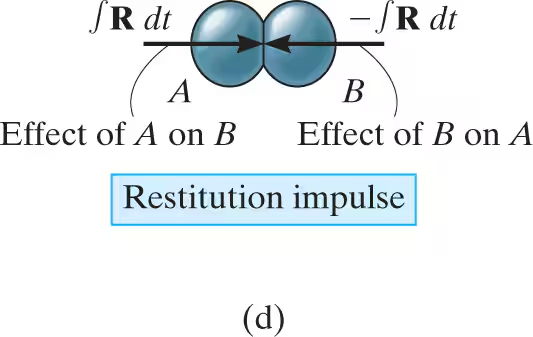
central impact diagrams: after impact

Just after separation the particles will have the final momenta shown where vB2>vA2.

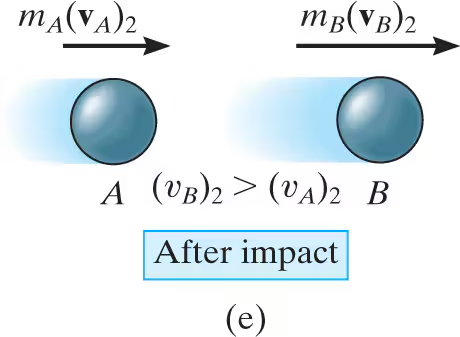
In most problems the initial velocities of the particles will be known, and it will be necessary to determine their final velocities vA2 and vB2. To do this we will need two equations that involve these unknowns.

The first equation requires conservation of momentum for the two particle systems

mA(vA)+mB(vB)1=mA(vA)2+mB(vB)2

To obtain a second equation, we will apply the principle of impulse and momentum to each particle.

This results in the coefficient of restitution equation, which expresses how elastic the collision is:

e(A)=v−vA2/vA1−v

e(B)= vB2-v/v-vB1

coefficient of restitution (e)

e= vB2-vA2/vA1-vB1 = rel. vel. after impact/ rel. vel. before impact

elastic impact

e=1

plastic impact

e=0

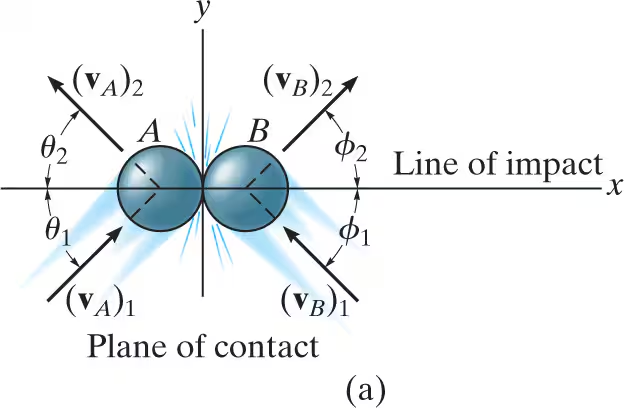
oblique impact image and unknowns

When oblique impact occurs between two smooth particles, the particles move away from each other with velocities having unknown directions as well as unknown magnitudes. Provided the initial velocities are known, then there are four unknowns in the problem. They are either vA2,vB2, θ2, and ϕ2, or the x and y components of the final velocities,

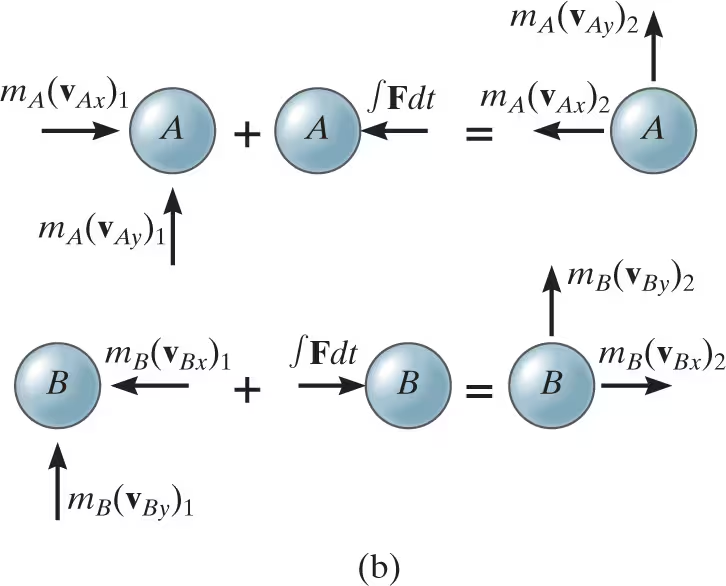
procedure for analysis: oblique impact: If the y axis is established within the plane of contact and the x axis along the line of impact, then the impulsive forces of deformation and restitution act

only in the x direction

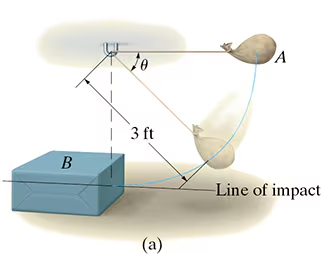
The bag A, having a weight of 6 lb, is released from rest at the position θ=0°, as shown. After falling to θ=90°, it strikes an 18-lb box B. If the coefficient of restitution between the bag and box is e=0.5, determine the velocities of the bag and box just after impact. What is the loss of energy during collision?

To solve this problem, we need to determine the velocities of bag A and box B just after impact and the energy lost during the collision. This requires using conservation of energy before impact and conservation of momentum during impact.

conservation of energy:

with the datum at theta=0, we have

T0+V0=T1+V1

0+0=1/2(6/32.2)(vA)1²-6(3);

vA=13.9

conservation of momentum:

mB(vB)1+mA(vA)1=mB(vB)2+mA(vA)2

0+6/32.2(13.9)=18/32.2(vB)2+6/32.2(vA)2

(vA)2=13.9-3(vB)2

since separation occurs after the collision, vB2>vA2,

e=(vB)2-(vA)2/(vA1)-(vB)1; .5=(vB)2-(vA)2/13.9-0

(vA)2=(vB)2-6.95

solving the two equations,

vA2=-1.74, vB2= 5.21.

LOSS OF ENERGY:

applying the principle of work and energy just before and after collision, we have

work= T2-T1

work (sum of U1-2)= [1/2(18/32.2)(5.21)²+1/2(6/32.2)(1.74)²]-[1/2(6/32.2)(13.9)²]

=-10.1

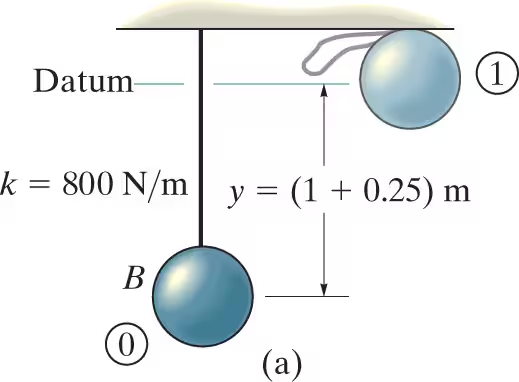
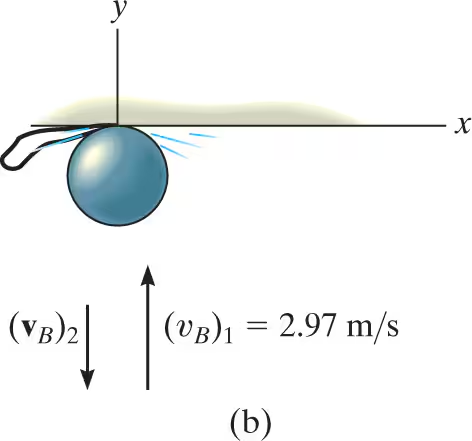
Ball B shown has a mass of 1.5 kg and is suspended from the ceiling by a 1-m-long elastic cord. If the cord is stretched downward 0.25 m and the ball is released from rest, determine how far the cord stretches after the ball rebounds from the ceiling and falls downward. The stiffness of the cord is  k=800 N/m, and the coefficient of restitution between the ball and ceiling is e=0.8. The ball makes a central impact with the ceiling.

The problem involves a ball suspended from an elastic cord that is released from a stretched position, rebounds off the ceiling, and then falls again. The solution follows three major steps:

1. Use conservation of energy to determine the velocity before impact.

2. Use the impulse-momentum principle (coefficient of restitution) to determine the velocity after impact.

3. Use conservation of energy again to determine the maximum stretch after the ball falls.

First we must obtain the velocity of the ball just before it strikes the ceiling using energy methods, then consider the impulse and momentum between the ball and ceiling, and finally again use energy methods to determine the stretch in the cord.

conservation of energy:

T0+V0=T1+V1

1/2m(vB)0²-WBy0+1/2ks²=1/2m(vB)1²+0

0-1.5×9.81×1.25+1/2(800)(.25)²=1/2(1.5)(vB)1²

vB1=2.968m/s

The interaction of the ball with the ceiling will now be considered using the principles of impact. The weight of the ball is considered a nonimpulsive force.

coefficient of restitution (principles of impact):

.8=(vB)2-0/0-2.968

(vB)2= -2.372m/s

conservation of energy: The maximum stretch s3 in the cord can be determined by again applying the conservation of energy equation to the ball just after collision

Why Use Conservation of Energy Here Again?

Now that the ball is moving downward after rebounding, it stretches the elastic cord again. To determine the maximum stretch (s3​), we apply conservation of energy:

T2​+V2​=T3​+V3​

1/2m(vB)2²+0=1/2m(vB)3²-WBy3+1/2ks3²

1/2(1.5)(2.37)=0-9.81(1.5)(1+s3)+1/2(800)

s3=237mm

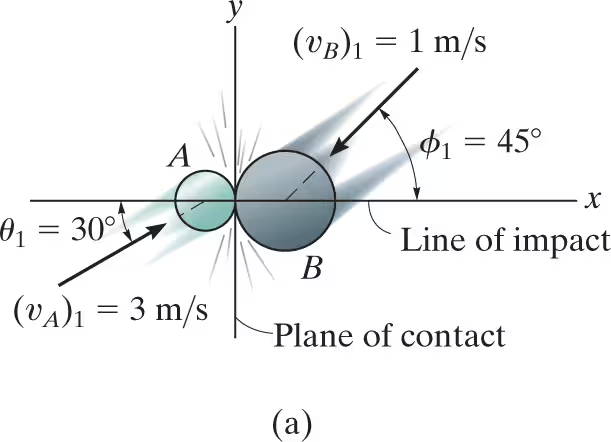
Two smooth disks A and B, having a mass of 1 kg and 2 kg, respectively, slide on the horizontal plane and collide with the velocities shown. If the coefficient of restitution for the disks is e=0.75, determine the x and y components of the final velocity of each disk just after collision.

conservation of x momentum:

mA(vAx)1+mB(vBx)1=mA(vAx)2+mB(vBx)2

solve for (vAx)2+2(vBx)2= 1.184

coefficient of restitution (x): .75=(vBx)2-(vAx)2/2.598-(-.7071)

solve for vAx2 and vBx2

conservation of y momentum:

mA(vAy)1=mA(vAy)2

mB(vBy)1=mB(vBy)2 solve for both vBy2 and vAy2

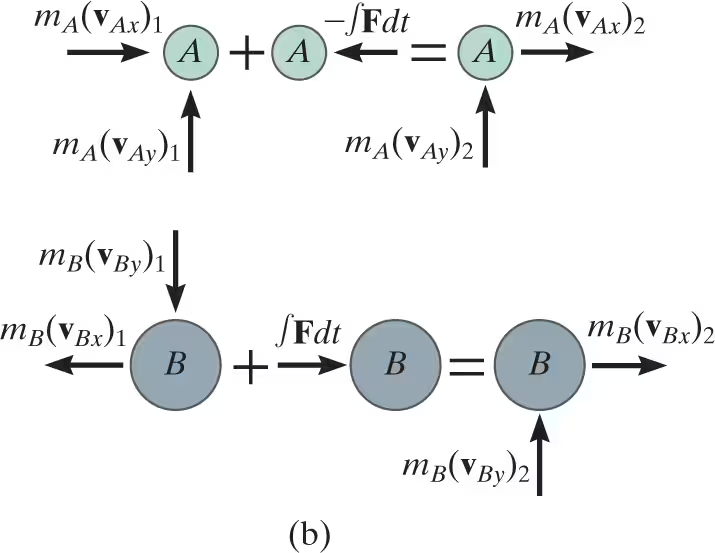
angular momentum (Ho)

The angular momentum of a particle about point O is defined as the “moment” of the particle’s linear momentum about O

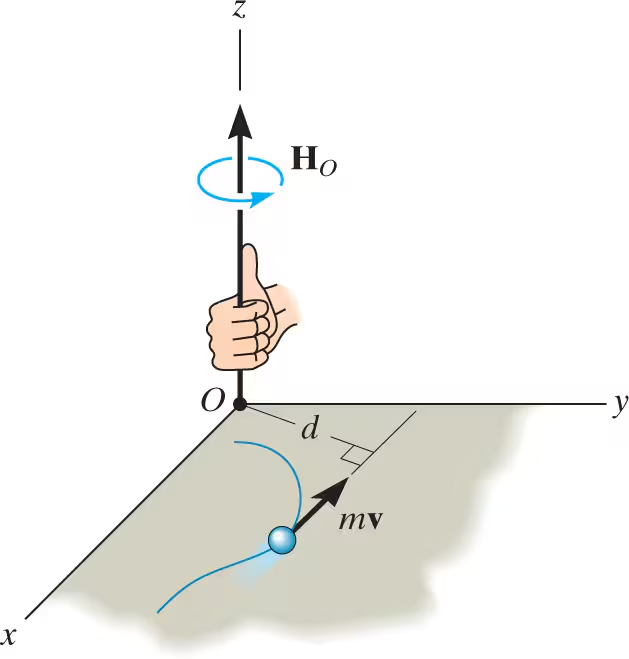
If a particle moves along a curve lying in the x–y plane, the angular momentum at any instant can be determined about point O (actually the z axis) by using a scalar formulation. The magnitude of HO is

dmv. Here, d is the moment arm or perpendicular distance from O to the line of action of mv.

units of angular momentum and direction

kg*m²/s or slug*ft²/s. The direction of HO is defined by the right-hand rule. As shown, the curl of the fingers of the right hand indicates the sense of rotation of mv about O, so that in this case the thumb (or HO) is directed perpendicular to the x–y plane along the +z axis.

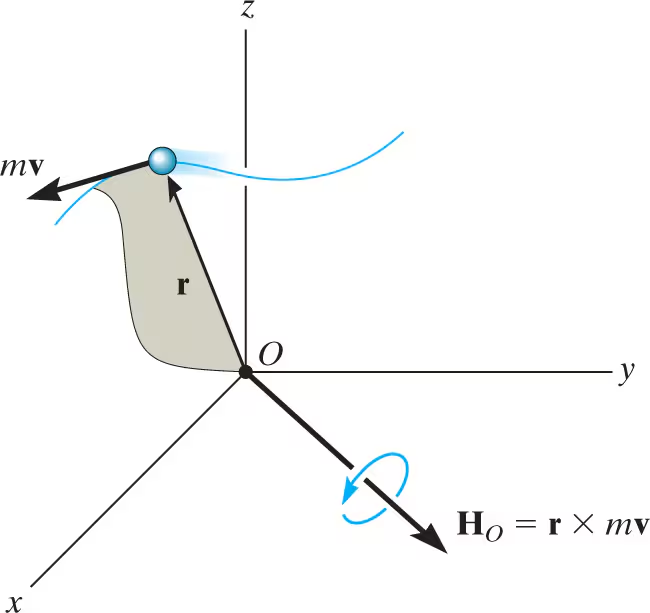
If the particle moves along a space curve, the vector cross product can be used to determine the angular momentum about O. In this case,

Ho= r x mv

Here r denotes a position vector drawn from point O to the particle. HO is perpendicular to the shaded plane containing r and mv.

If r and mv are expressed in terms of their Cartesian components, then the angular momentum can be determined by evaluating the determinant:

HO=

i j k

rx ry rz

mvx mvy mvz

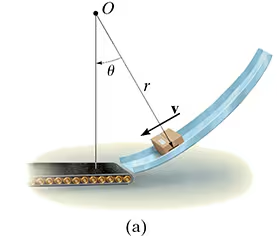
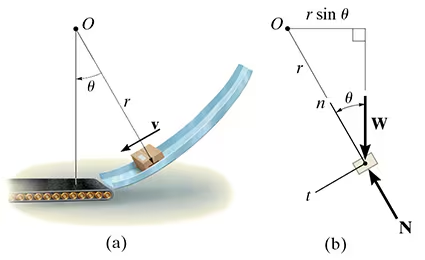
The box shown has a mass m and travels down the smooth circular ramp such that when it is at the angle θ it has a speed 𝑣v. Determine its angular momentum about point O at this instant and the rate of increase in its speed, i.e., at.

A box of mass mmm slides down a smooth circular ramp and at some angle θ\thetaθ has a velocity v. We need to determine:

1. Angular momentum about point O.

2. The rate of increase in speed (at​=dv​/dt).

Definition of Angular Momentum

The angular momentum of a particle moving with velocity v about a point O is given by:

HO​=r×mv

Since the velocity v is tangential to the path, and the radius r is perpendicular to v, the magnitude of the angular momentum simplifies to:

HO​=rmv

Thus, the angular momentum of the box about O is:

HO​=rmv

it can be seen that only the weight W=mg contributes a moment about point O.

so, mgrsintheta= rmdv/dt

dv/dt= gsintheta

principle of angular impulse and momentum

HO1+sum(St1 to t2 MOdt)=HO2

The initial and final angular momenta HO1 and HO2 are defined as the moment of the linear momentum of the particle HO=r×mv at the instants t1 and t2, respectively. The second term on the left side,  ∑∫MO dt, is called the angular impulse. It is determined by integrating, with respect to time, the moments of all the forces acting on the particle over the time period t1 to t2.

moment of a force around point O

MO= r x F

angular impulse in vector form

S from t1 to t2 of MO dt= S from t1 to t2 of r x F dt

impulse and momentum principles two equations

mv1 + sum S from t1 to t2 of Fdt= mv2

HO1 + sum S from t1 to t2 of MOdt= HO2

conservation of angular momentum

When the angular impulses acting on a particle are all zero during the time t1 to t2

HO1=HO2

This equation is known as the conservation of angular momentum. It states that from t1 to t2 the particle’s angular momentum remains constant.

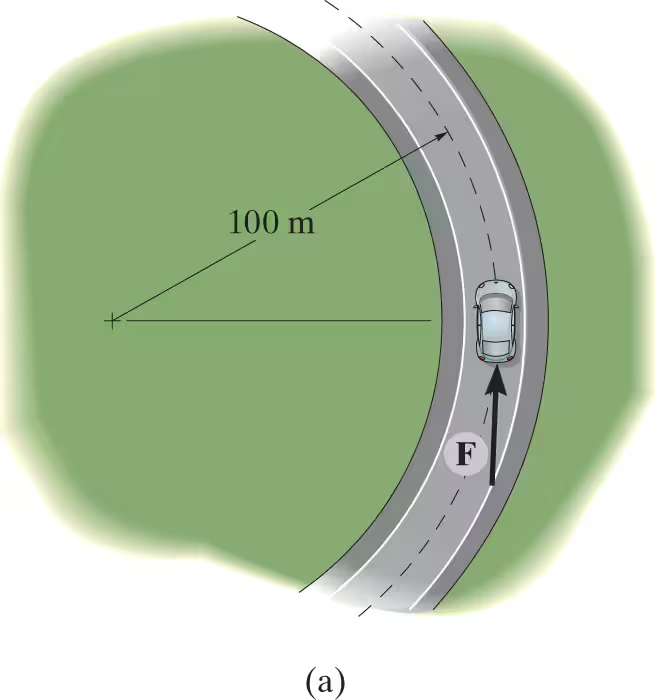
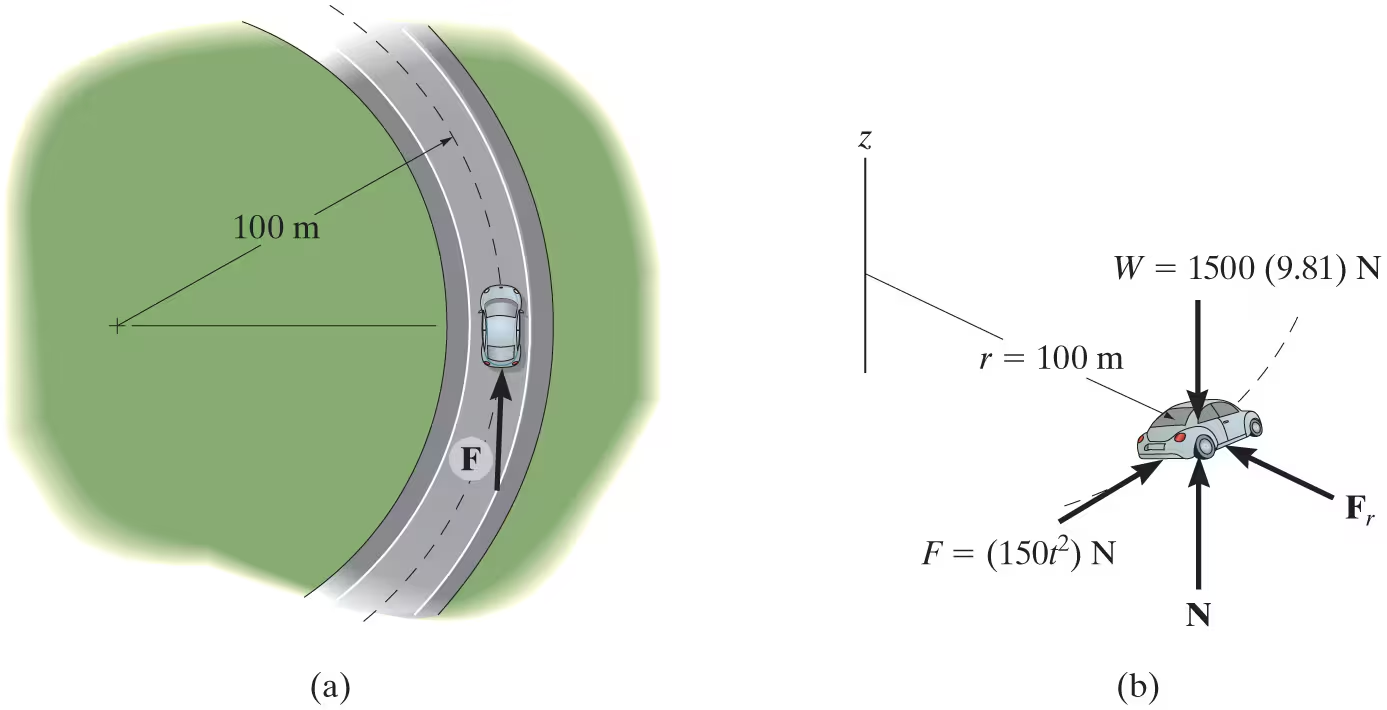
The 1.5-Mg car travels along the circular road as shown. If the traction force of the wheels on the road is  F=150t2 N, where t is in seconds, determine the speed of the car when  t=5 s. The car initially travels with a speed of 5 m/s. Neglect the size of the car.

If we apply the principle of angular impulse and momentum about the z axis, then the angular impulse created by the weight, normal force, and radial frictional force will be eliminated since they act parallel to the axis or pass through it.

Hz1 + sum S from t1 to t2 of Mz dt = Hz2

rm(v)1+S from t1 to t2 of rFdt= rm(v)2

100×1500×5+S from 0 to 5 of 100(150t²)Ndt

v2=9.17