MATH 161: Unit One
5.0(1)
Studied by 18 people
Call Kai
Learn
Practice Test
Spaced Repetition
Match
Flashcards
Knowt PlayCard Sorting
1/32
Earn XP
Description and Tags
Last updated 2:35 AM on 8/30/23
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
33 Terms
1
New cards
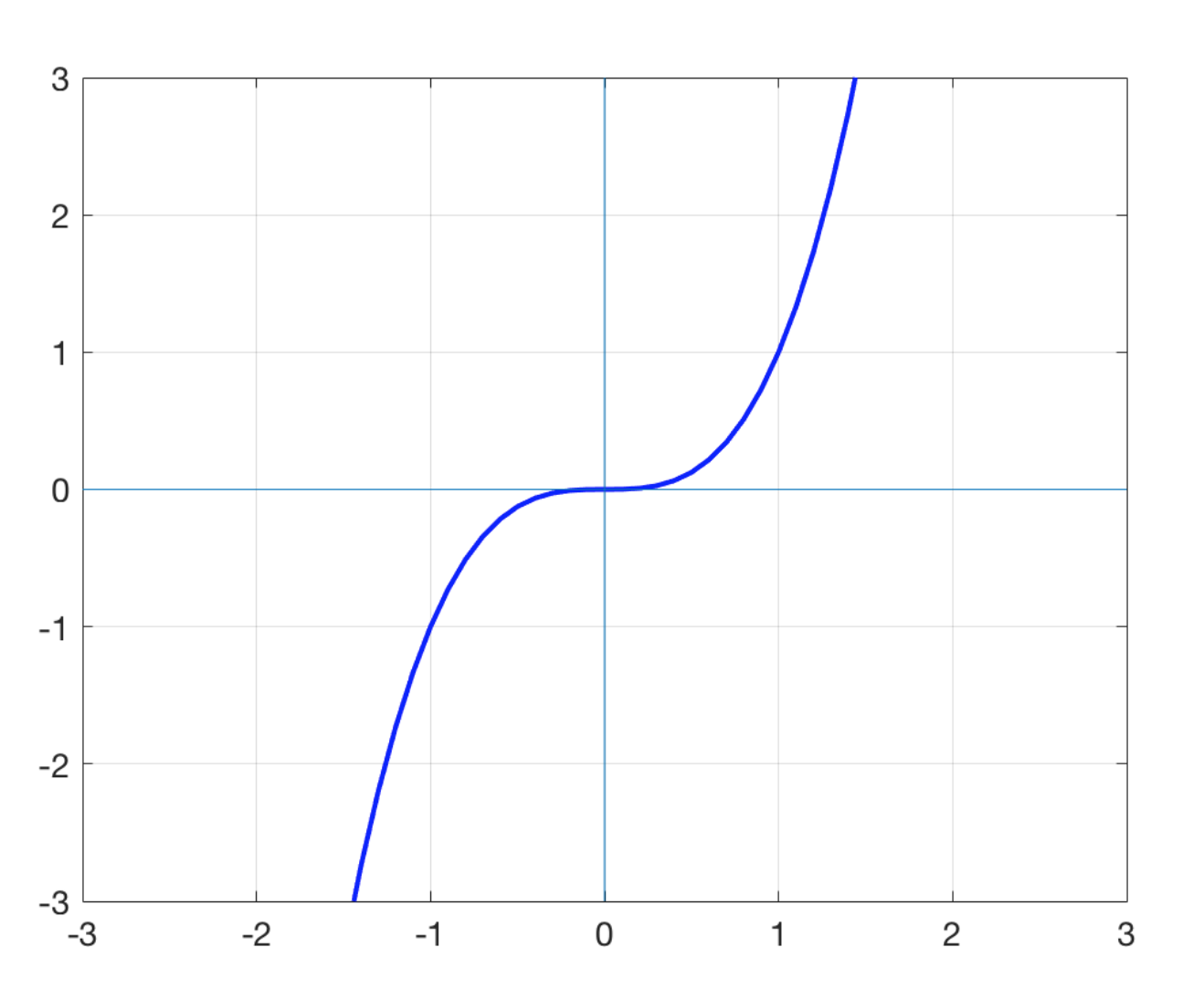
f(x)=
x^3
2
New cards
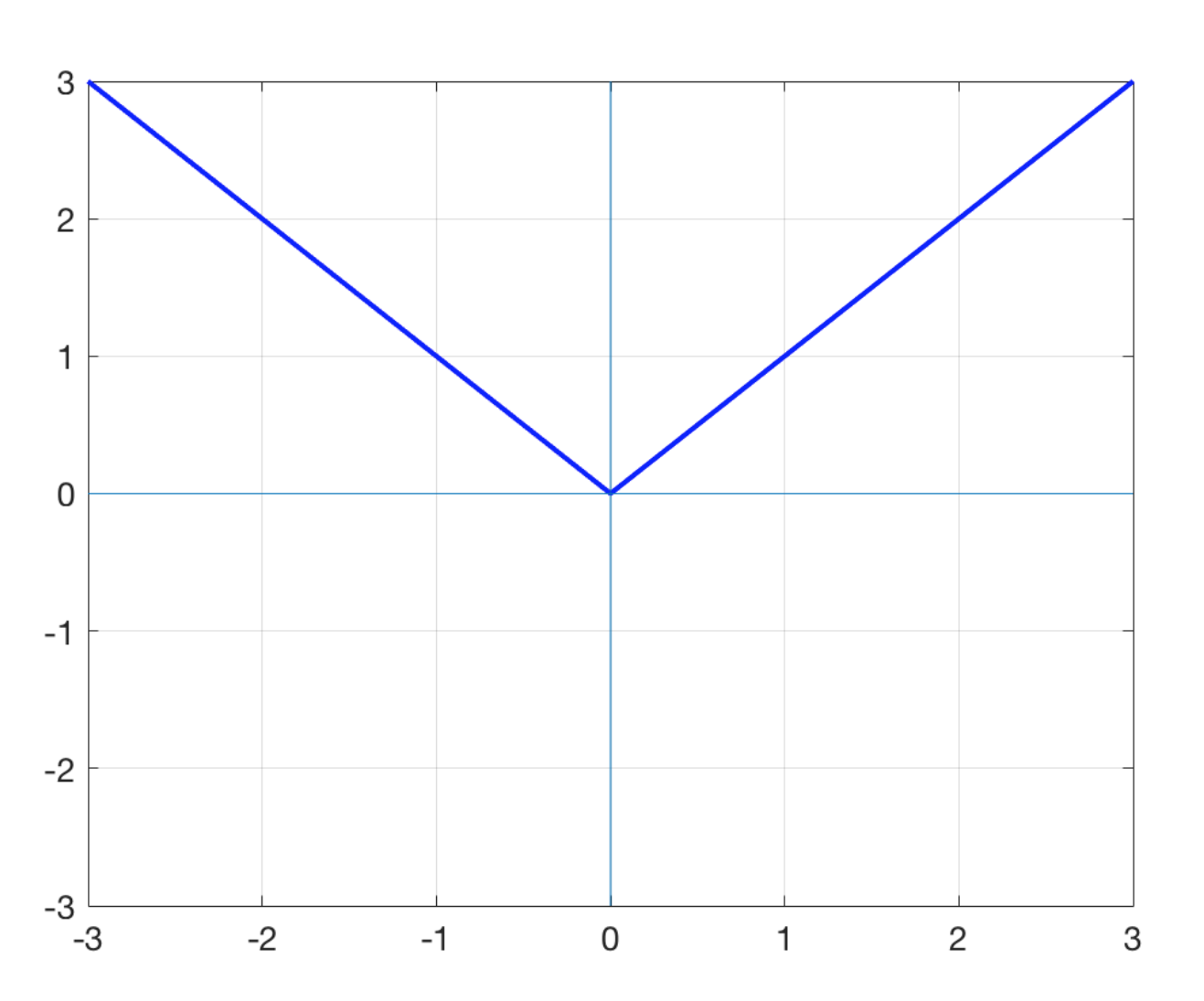
f(x)=
IxI
3
New cards
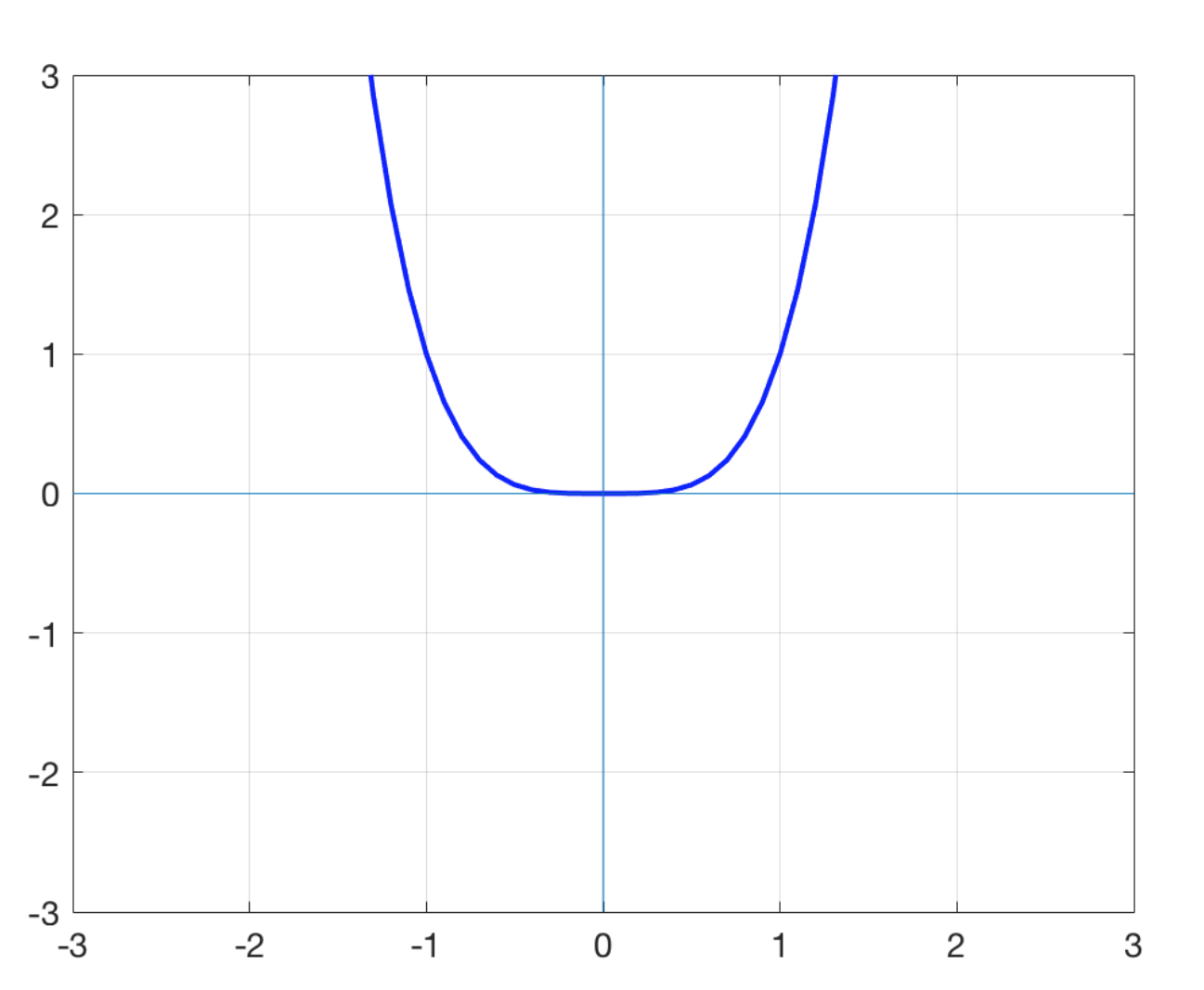
f(x)=
x^4
4
New cards
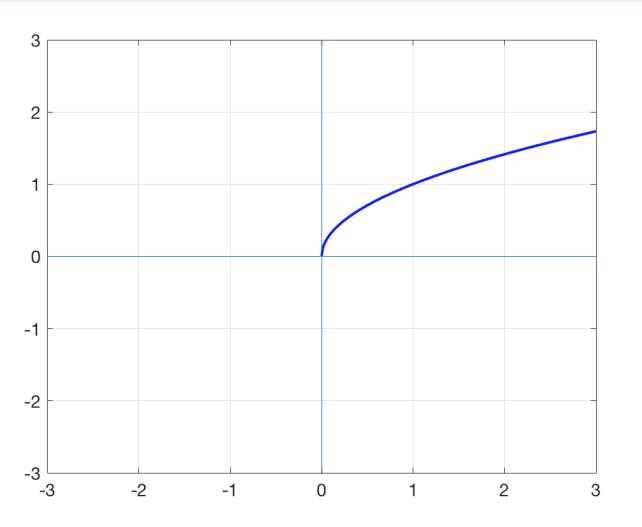
f(x)=
√x
5
New cards
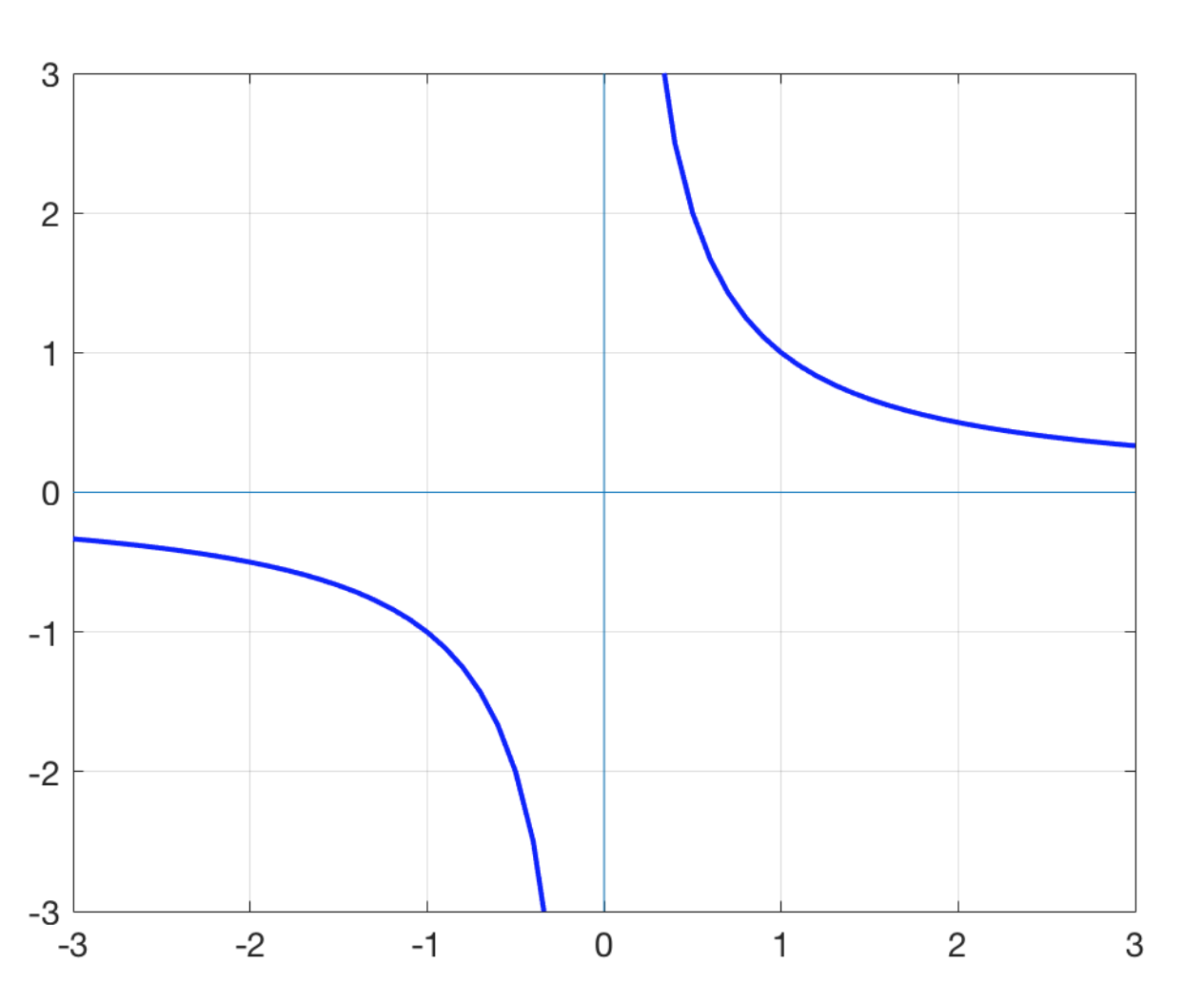
f(x)=
1/x
6
New cards
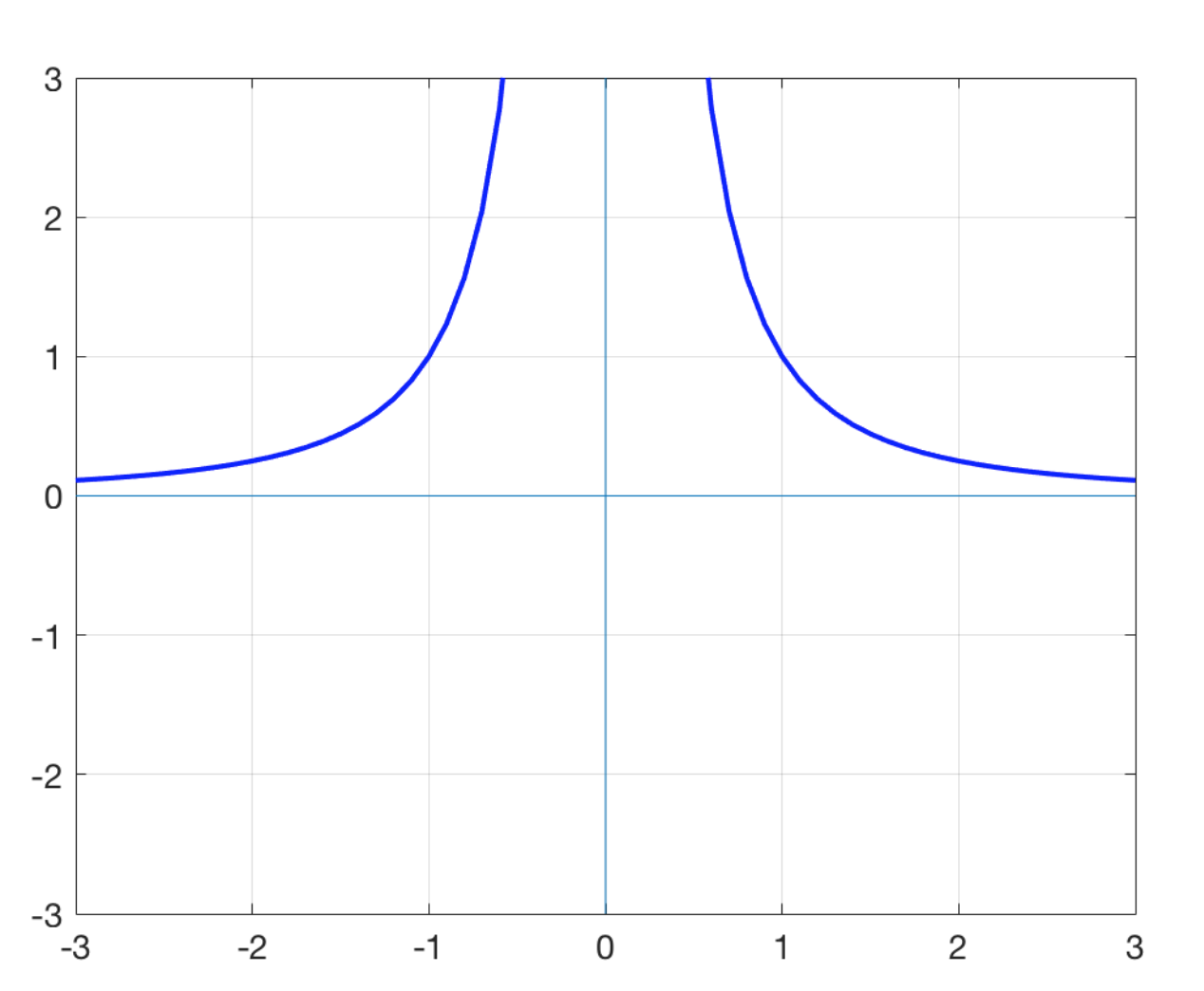
f(x)=
1/x^2
7
New cards
domain for polyomials
(-∞,∞)
8
New cards
domain for fractions
x=0
9
New cards
notation of domain for fractions
(-∞,undefined)U(undefined,∞)
10
New cards
domain for radicals
radicand≥0
11
New cards
notation of domain for radicals
(-∞,undefined radicand\] or \[undefined radicand,∞)
12
New cards
domain for radicals in the denominator of a fraction
radicand>0
13
New cards
notation for domain for radicals in the denominator of a fraction
(-∞,undefined radicand)U(undefined radicand,∞)
14
New cards
radian and degree conversion
π/180°
15
New cards
addition formula for sin
sin(x+y)=sinxcosy+cosx+siny
16
New cards
addition formula for cos
cos(x+y)=cosxcosy-sinxsiny
17
New cards
addition formula for tan
tan(x+y)=\[tanx+tany\]/\[1-tanxtany\]
18
New cards
double angle formula for sin
sin2x=2sinxcosx
19
New cards
double angle formula for cos
cos2x=cos^2x-sin^2x
20
New cards
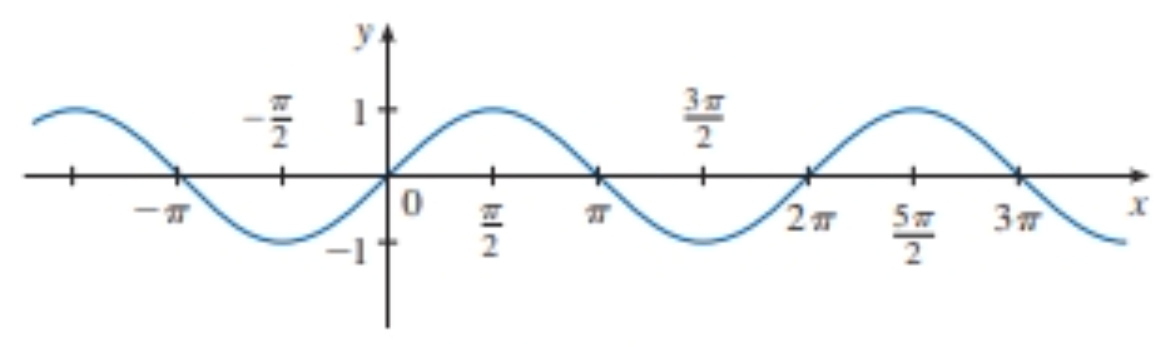
f(x)=
sinx
21
New cards
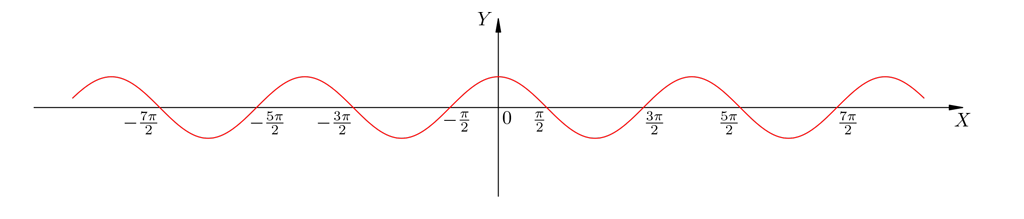
f(x)=
cosx
22
New cards
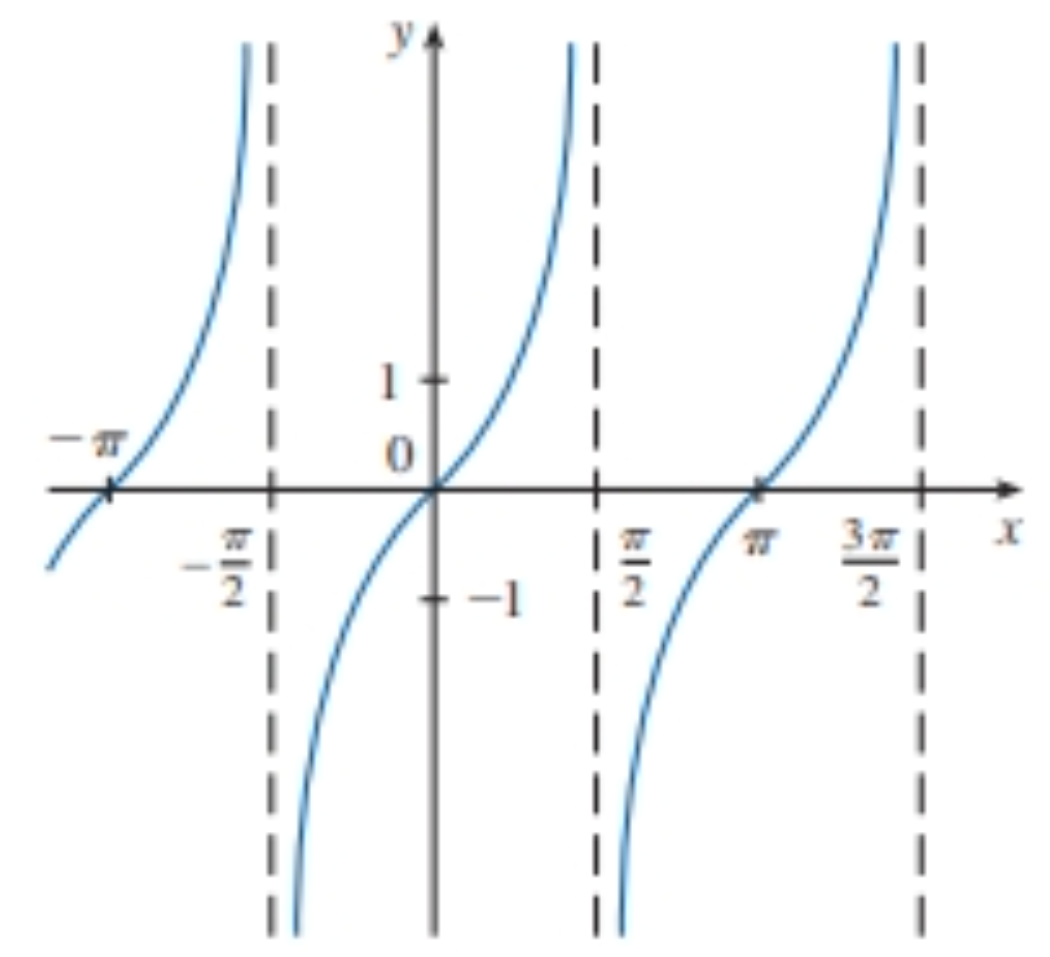
f(x)=
tanx
23
New cards
trig identity of sin and cos = 1
sin^2x+cos^2x=1
24
New cards
definition of a limit (description)
the limit of *f(x)* as *x* approaches *a*, equals *L*
25
New cards
definition of a limit (formula)
lim *f(x)* = *L*
(*x–>a*)
(*x–>a*)
26
New cards
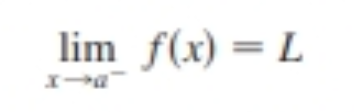
definition of one-sided limits (left-hand limit)
the limit of *f(x)* as *x* approaches *a* **from the left** is equal to *L*
27
New cards
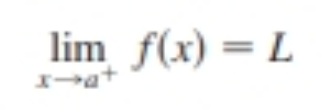
definition of one-sided limits (left-hand limit)
the limit of *f(x)* as *x* approaches *a* **from the right** is equal to *L*
28
New cards
the limit of f(x) = L as x–>a \[is defined if\]
the left and right limits are the same
29
New cards
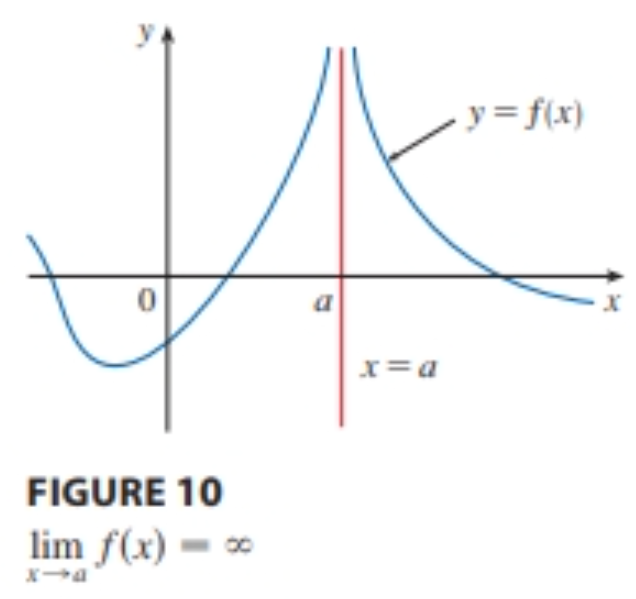
infinite limits are _
vertical asymptotes
30
New cards
function *f* is **continuous at a** **number** *a* if (reason 1/3)
*f(a)* is defined \[*a* is the domain of *f*\]
31
New cards
function *f* is **continuous at a** **number** *a* if (reason 2/3)
*lim f(x)* exists \[the left and right limits are the same\]
32
New cards
function *f* is **continuous at a** **number** *a* if (reason 3/3)
lim f(x) = f(a)
33
New cards
speed is the _ of distance over time
slope
Note 
Flashcards (260)