Comparing 2 Proportions

In contrast to one-proportion problems, 2-proportion problems..

give 2 different groups (no baseline or null → need to COMPARE the 2 groups)

Standard Deviation of the Difference b/w 2 proportions

SD(p-hat(1) - p-hat(2))= sqr( (p1q1/n1) + (p2q2/n2)

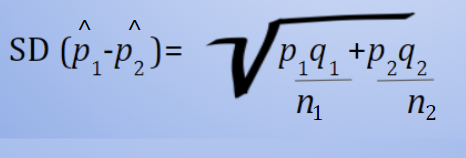
Assumptions and Conditions

• Independent Assumption (w/in each group)

• Success/Failure Condition

• Independent Group Assumption (b/w groups)

  • Randomization Condition

  • 10% Condition

Independent Group Assumption

The 2 groups we’re comparing must be independent of each other (most important assumption, if violated then the methods won’t work)

PANIC for difference b/w 2 proportions

• Parameter of interest: “Im interested in determining how effective ___ is”

• Assumptions and Conditions: Independence and Independence Group Assumption, Randomization Condition, 10% Condition, Success/Failure Condition

• Name Interval: “B/c my conditions are satisfied I can use a Normal Model to construct a 2-propotion z-interval”

• Interval Calculation: 1st identify variables (p1,n1,p2,n2) → CI: estimate (p-hat(1) - p-hat(2)) ± ME (z* x SE(p-hat(1) - p-hat(2))

• Conclusion in Context: “Im #% confident that ___ could affect the proportion b/w (CI lower bound)% and (CI upper bound)%

Null Hypothesis for Difference b/w 2 proportions

H0: p1=p2 or p1-p2=0 [Hypothesizing that there’s NO difference in the proportions)

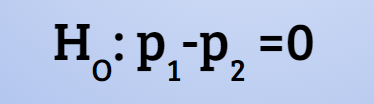
Pooling

combining counts to get an estimated overall proportion

Pooled proportion

P(pooled)= (sucess1 + success2)/ n1+n2

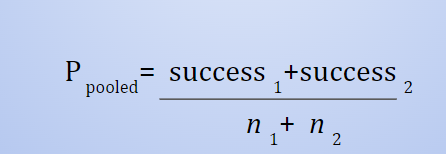
SE for 2 proportion z-test

SEpooled (p1-p2)= sqr( (p(pooled) x q(pooled))/n1) + (p(pooled) x q(pooled))/n2)

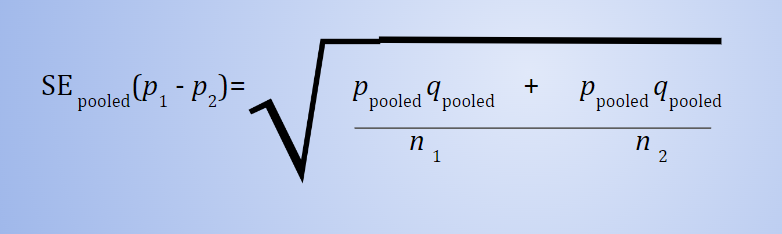
PHANTOMS for difference b/w 2 proportions

• Parameter of Interest is same as CI

• Hypotheses: H0: p1-p2=0; HA: p1-p2 does NOT equal 0 (can be inequalities such as < and >)

• Assumptions and Conditions is same as CI

• Name Test: “B/c my conditions are satisfied I can use a Normal Model to construct a 2-propotion z-test”

• Test Statistic: calculate p(pooled) and SE(pooled(p1-p2) to get z-score ( ((p1-p2)-0/H0)/SEpooled(p1-p2)

• Obtain P-value: P(z(inequality) z-score)

• Make a Decision: “W/ a P-value so low/high, I will(low)/ wont (high) reject H0. If H0 were true, I would see the observed difference I have (P-value as %) of the time”

• State Conclusion in Context: “ There is(low)/isnt(high) strong evidence that there’s an effect w/ the modification

If we have an experiment where the groups result from random allocation of subjects into treatments..

Independent Group Assumption is NOT reasonable

What can go wrong?

• Dont use 2 sample proportion methods when the samples arent independent

• Dont apply inference methods when there’s no randomization

• Dont interpret the significant different of proportions causally