Math Review

Describe a rational number that is greater than 3.456 but smaller than 3.457. Explain how you know the number is rational.

3.456 < 3.4561 < 3.4573.4561 is rational because it terminates

Every integer is a real number.

True

Every integer is a natural number

False

Every irrational number is a real number

True

Every integer is a rational number

True

Between every two rational numbers there is a rational number.

True

If a real number has an infinitely long decimal expansion, then it must be an irrational number.

False

There is no real number between 0.123333333 . . . and 0.124.

False

what is Cardinality, give an example

the “size” of a set, 50 states 50 stars on the flag or 60 secs in a min 60 min in an hour

what is 1-to-1 correspondence

Two collections of objects are equally numerous, precisely if there is a one-to-one correspondence between the elements of the two collections. Ex: Natural numbers to odd numbers

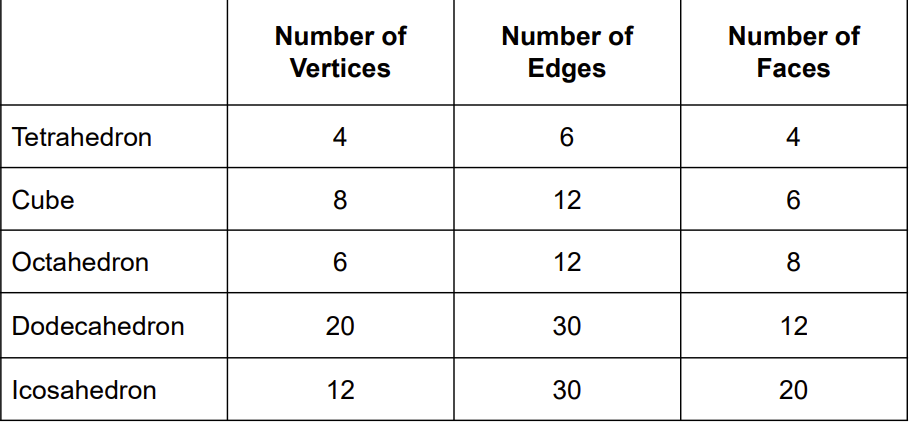
The Five Platonic Solids

Tetrahedron, Cube, Octahedron, Dodecahedron, Icosahedron

What is the table for the 5 solids

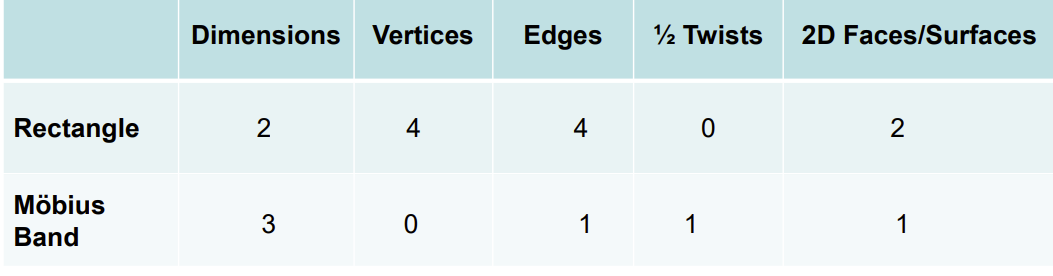
Two objects are equivalent by distortion…

if we can stretch, shrink, bend, or twist one, without cutting or gluing, and deform in into the other.

Möbius Band vs. Rectangle

examples of objects in our world which may at times have knots?

Computer Cords Headphone Cords DNA RNA Proteins Fishing Line Necklaces Extension Cords Strings of Holiday Lights Neck Ties

What is the most useful knot to know how to tie?

Square knot

Dr. Austin said that EVERY cell of EVERYorganism we have ever studied has an enzyme that can unknot knots, unlink links in DNA. This enzyme gets its name from the amazing branch of mathematics known as topology (aka. rubber sheet geometry). What was the name of this enzyme

Topoisomerase

What is an Euler Circuit

An Euler Circuit is a path that traverses each edge of a graph exactly once, reaches every vertex, and returns to the starting vertex.

Euler’s Circuit Theorem

A connected graph has an Euler circuit if and only if every vertex has an even number of edges meeting at that vertex.

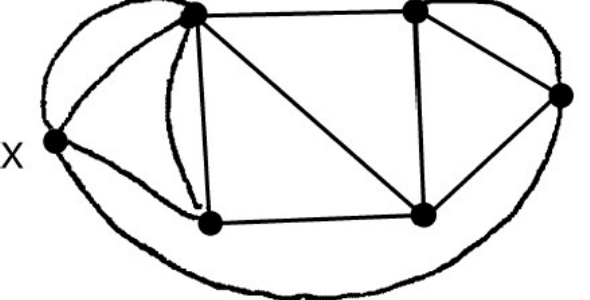
Does this graph have an Euler Circuit?

Yes! We know this because each vertex has two (an even number) of edges meeting at that vertex

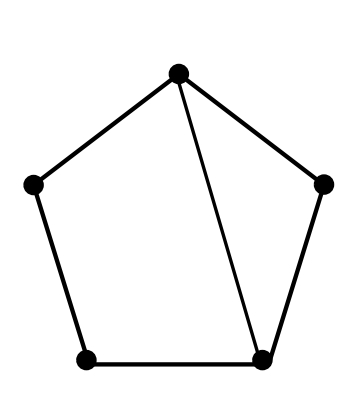
Does this graph have an Euler Circuit?

No! We know this because each vertex does NOT have an even number) of edges meeting at that vertex. We see two vertices that have 3 edges meeting there

For any connected graph in the plane,V – E + F = 2,

V is the number of vertices, E is the number of edges, and F is the number of regions

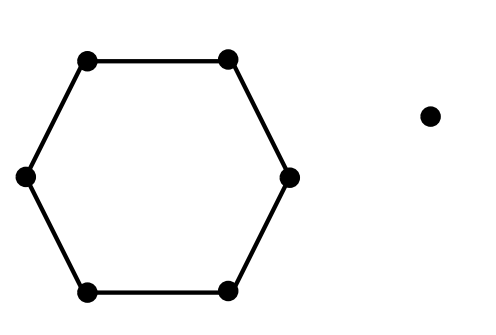
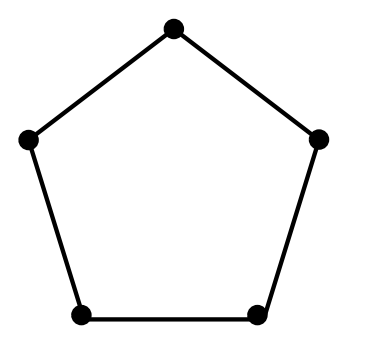
Complete the following table for the graph shown.

Example of a fractal

Probability: Rolling a 2 three times in a row with a fair die

P(222) = (1/6)^3 = 1/6x1/6x1/6

probability: Selecting a King from a regular deck of cards, given that a Queen was previously removed from the deck

P(King given a Queen already) = 4/51

probability: Selecting a King from a regular deck of cards, given that a King was previously removed from the deck

P(King given a King already) = 3/51

probability : Flipping a coin four times and seeing at least one head

P(HHHH) = (1/2)^4 = 1/2x1/2x1/2x1/2 P(Flip 4X & see at least one Head) = 1 – P(TTTT)= 1- (1/2)^4 = 1- 1/2x1/2x1/2x1/2= 1 – 1/16 = 15/16

Suppose you have the 26 letters of the alphabet on separate cards in a hat. You pick out a card, write down the letter, put the card back in the hat, mix up the cards, pick out another card, and so on. Write an expression for the probability that on your first five draws your letters spell TEXAS

P(TEXAS)=1/26x1/26x1/26x1/26x1/26=(1/26)

How many different 4-letter "words" are there (they don't have to be real words) made from a 26-letter alphabet? (Letters can repeat. Give an expression for this answer. Do not evaluate your expression.)

26x26x26x26 = 264

In a standard deck of 52 cards, what is the smallest number of cards you must draw to guarantee that you will have 3 cards of one suit? (Remember, a standard deck of cards has four suits with 13 cards in each suit.)

9