AP Precalculus Unit 3 Notes
3.1: Periodic Phenomena
Periodic Phenomena: occurrences or relationships that display a repetitive pattern over time or space.
Ex: undulating motion of waves, the circular rotation of clock hands, and the fluctuation in daylight hours throughout the year
Key Details of Graphs:
Periodic Function: A function that replicates a sequence of y-values at fixed intervals
Period: The gap between repetitions of a periodic function. Represents the length of one complete cycle
Intervals of Increase and Decrease: Define sets of x-values from the lower to the maximum point and from the upper to the minimum point, respectively
Concavity: when rate of intervals of increase/decrease is changing
Average Rate of Change: change in output divided by the change in input
3.2: Sine, Cosine, and Tangent
Standard Position Angles
Angles are like shapes formed where two lines, parts, or beams meet.
When describing an angle by its rotation, the starting point is called the initial side, and the endpoint after the rotation is the terminal side. This is called standard position
Rotations include positive and negative angles
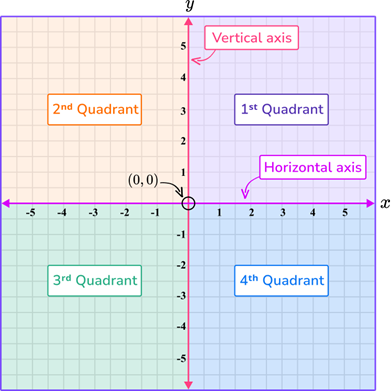
Standard Position: If an angle's initial side is parallel to the positive x-axis and its vertex is at the origin, it is said to be in the standard position.
Initial Side: The ray on the x-axis
Terminal Side: An angle's other ray in standard position
Positive Angle: When something is rotated counterclockwise
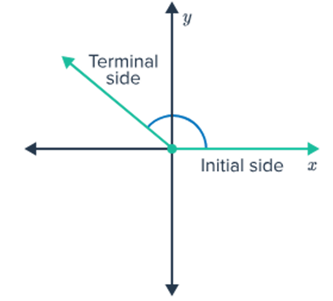
Negative Angle: When something is rotated clockwise
Radian Angle Measures
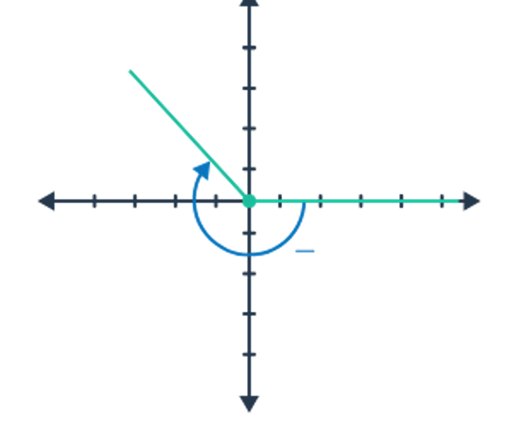
Can find the measure of an angle in radians by using the formula θ=s/r, where s is the arc length, and r is the circle's radius.
With circles with a radius of one unit, an angle of 11 radians would be the measure of an angle subtended by an arc of length 11 units.
The entire distance around a circle with a radius of one unit, or its circumference C, is 2π (since C=2πr). This means a complete turn around the circle corresponds to an angle of 2π radians, equivalent to 6.28 radians or 360 degrees.
Since half a circle is π radians (as π radians equals 180 degrees), angles can be expressed as radians as fractions of π.
1 | 3/4 | 2/3 | 1/2 | 1/3 | 1/4 | 1/6 | 1/8 | 1/12 | |
|---|---|---|---|---|---|---|---|---|---|
Measure in degrees | 360° | 270° | 240° | 180° | 120° | 90° | 60° | 45° | 30° |
Measure in radians | 2π | 3/2π | 4/3π | π | 2/3π | π/2 | π/3 | π/4 | π/6 |
Coterminal Angles
Angles spin more than once, and their measures go beyond 2π radians.
Due to how angles are defined through rotation, it's conceivable to have two angles sharing the same starting and ending positions but having different measures. These related angles are known as coterminal angles.
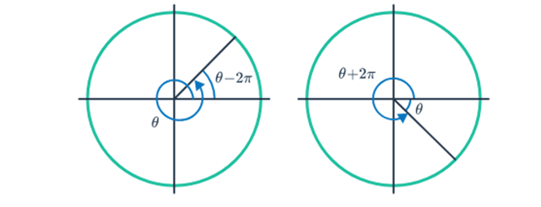
If two angles end up in the same position, one might be a full rotation or more ahead or behind the other. The difference in their measures is like going around the circle several times.
For the unit circle (a circle with a radius of one), angles measured starting from the positive x-axis. Even if an angle goes beyond one complete turn around the circle, its trigonometric functions are related to those of an angle in the first quadrant.
3.3: Sine and Cosine Functions Values
Sine and Cosine Functions and the Unit Circle
Special Triangles:
Special triangles on the unit circle aid in evaluating trigonometric functions with exact ratios.
45°-45°-90° Triangle:
Side lengths ratio - 1:1:1 times square root of 2
30°-60°-90° Triangle:
Side lengths ratio -1: 1 times square root of 3: 2
To Calculate:
Calculate the legs of each triangle, keeping your answer in fraction form.
Write the ordered pair that represents the endpoint of each radius on each unit circle.
3.4: Sine and Cosine Functions Values
Graphing the Sine Function
Use unit circle angles for x-axis representation.
Coordinate range: [−1,1] for the y-axis.
Explore the relationship between the unit circle and the sine graph.
Graphing the Cosine Function
Use unit circle angles for x-axis representation.
Coordinate range: [−1,1] for the x-axis.
Explore the relationship between the unit circle and the cosine graph.
3.5: Sinusoidal Functions
Sinusoidal Functions
Sine (sinθ) and cosine (cosθ) functions share a sinusoidal nature, exhibiting the same shape and traits, elucidated through their phase shift.
Key Characteristics of the Sine Function
Phase Shift:
It denotes the horizontal shift in a sine or cosine function upon adding an angle.
For instance, π to sinθ results in sinθ+π.
The shift in direction becomes evident after isolating sinθ.
Example: If sinθ+π=0, then sinθ=−π.
Due to the negative measure of the added angle, sinθ shifts π units to the left.
Sine Function Transformation: sin(θ)→sin(θ+π)→cos(θ).
Key Characteristics of the Cosine Function
Phase Shift:
It represents the horizontal shift in sine or cosine functions upon adding an angle.
Analogous to the phase shift of the sine function.
Cosine Function Transformation: cos(θ)=sin(θ+π).
Features
Both sine and cosine functions possess sinusoidal traits, sharing the same shape and features.
The phase shift occurs with the addition of π.
Both are same
Sine function key features:
Domain: (−∞,∞)(−∞,∞)
Range: [−1,1][−1,1]
Period: 2π
Frequency: 1/2π
Amplitude: 1
Midline: y=0
Cosine function key features:
Domain: (−∞,∞)
Range: [−1,1]
Period: 2π
Frequency: 1/2π
Amplitude: 11
Midline: y=0
3.6: Sinusoidal Function Transformations
Transformations of Sine and Cosine Functions
Transformations modify the critical features of sine and cosine functions.
An exploration involving sliders helps understand the impact of changes on the graph.
Sinusoidal Function
Sinosoidal Function: A function in y=asin[b(x−c)]+d represents a sine wave pattern.
Parameters:
A (Amplitude): Vertical stretch for ∣a∣>1, vertical compression for ∣a∣<1, and reflection across the x-axis for a<0.
b (Period): 2π/b, with horizontal compression for ∣b∣>1, horizontal stretch for ∣b∣<1, and reflection across the y-axis for b<0.
c (Phase Shift): Horizontal translation by c units.
d (Vertical Shift): Vertical translation by d units.
3.7: Sinusoidal Function Context and Data Modeling
Interpreting, Verifying, and Reporting with Models
When dealing with periodic phenomena problems, select a suitable model and ensure its verification by applying it to a problem situation.
Reporting with a model involves presenting relevant information to the audience and providing enough detail for understanding without delving into technical algebraic work or confusing mathematical jargon.
3.8: The Tangent Function
Graphing the Tangent Function
The tangent function, f(θ)=tanθ, is periodic, with a domain and range based on the unit circle.
It's undefined where cosθ=0, leading to a discontinuous function with a period of π.
The tangent function, f(θ)=tanθ, is transformed by adjusting frequency and midline.
The general form of the tangent function is f(θ)=atan[b(θ−c)]+d.
Key Features
Tangent Function [tan(θ)]:
Domain: θ≠2π+nπ, n is any integer
Range: (−∞,∞)
x-Intercept: θ=nπ,n is any integer
y-Intercept: 0
Period: π
Amplitude: None
Midline: 0
Transformations of the Tangent Function
General Form: f(θ)=atan[b(θ−c)]+d
Vertical Stretch/Compression:
∣A∣>1 is a vertical stretch.
∣A∣<1 is a vertical compression.
A <0 is a reflection across the x-axis.
Period:
b>1 is a horizontal compression.
0<∣b∣<1 is a horizontal stretch.
b<0 is a reflection across the y-axis.
Phase Shift:
Horizontal translation by c units.
Vertical Translation:
Vertical translation by d units.
3.9: Inverse Trigonometric Function
Introduction to Inverse Trigonometric Functions
The inverse trigonometric functions: arcsin (sin-1), arccos (cos-1), and arctan (tan-1)
The reciprocal relationship holds f(f -1(x))=x and f -1(f(x))=x.
sin(arcsinx)=x and arcsin(sinx)=x
cos(arccosx)=x and arccos(cosx)=x
tan(arctan)=x and arctan(tanx)=x
Developing Analytical and Graphical Representations
Finding the inverse function involves reflecting the original function about the line y=x.
Crucially, the inverse function must be one-to-one and comprehensively cover the complete range of sine values.
Mathematicians often choose a domain, such as [−2π,2π], for sine, resulting in the representation sin-1(x).
This also applies to the functions of cosine and tangent
3.10: Trigonometric Equations and Inequalities
Solving Trigonometric Equations
Trigonometric equations involve one or more of the six trigonometric functions: sine, cosine, tangent, cosecant, secant, and cotangent
Addressing trigonometric equations requires various strategies, including inverse functions and algebraic manipulations.
Solve Using Reciprocal Functions
Reciprocal trigonometric functions, including cosecant (cscθ), secant (secθ), and cotangent (cotθ), relate to the fundamental trigonometric functions
cscθ=1/sinθ
secθ=1/cosθ
cotθ=cosθ/sinθ
Solve Using the Unit Circle
For any point (x,y) on the unit circle corresponding to an angle θ, the trigonometric functions are defined as follows:
x=cosθ
y=sinθ
x/y=tanθ
Utilizing the unit circle, solutions to equations like sinθ=0 are determined within specified domains.
3.11: Secant, Cosecant, and Cotangent Functions
Key Features and Characteristics
Cosecant Function:
Domain: θ≠nπ,n is any integer
Range: (−∞,−1]∪[1,∞)
x-Intercept: None
y-Intercept: None
Period: 2π
Amplitude: None
Midline: y=0
Secant Function:
Domain: θ≠(2n+1)π/2,n is any integer
Range: (−∞,−1]∪[1,∞)
x-Intercept: None
y-Intercept: y=1
Period: 2π
Amplitude: None
Midline: y=0
Cotangent Function:
Domain: θ≠nπ,n is any integer
Range: (−∞,∞)
x-Intercept: x=2π+nπ,n is any integer
y-Intercept: None
Period: π
Amplitude: None
Midline: y=0
3.12: Equivalent Representations of Trigonometric Functions
Pythagorean Identity
The Pythagorean identity relates the trigonometric functions of a right triangle.
sin2θ+cos2θ=1
Sine and Cosine Sum Identities:
sin(α+β)=sinαcosβ+cosαsinβ
cos(α+β)=cosαcosβ−sinαsinβ
These identities are valuable tools for rewriting expressions involving sums of angles.
3.13: Trigonometry and Polar Coordinates
Polar Coordinates
A polar coordinate system involves measurements of distance (r) from the origin and angle (θ) from the positive horizontal axis (polar axis).
Denoted as (r,θ), polar coordinates differ from Cartesian coordinates (x,y).
The rectangular plane is often called the Cartesian or rectangular coordinate system.
Convert complex numbers from rectangular (a+bi) to polar coordinates r(cosθ+isinθ), utilizing cosθ and sinθ to express x and y, respectively.
3.14: Polar Function Graphs
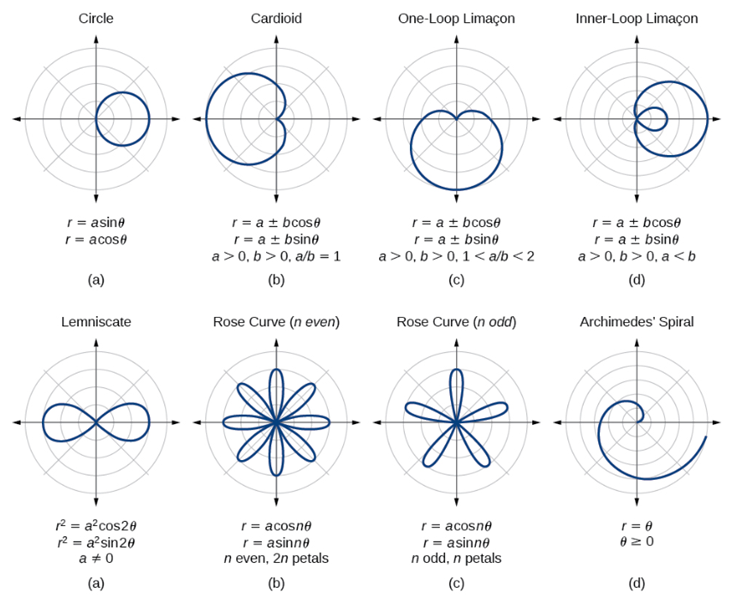
Circles
Polar functions express circles as r=a, where a is the radius.
General Form of a Circle: Circle equations in polar form: r=acosθ or r=asinθ.
Characteristics:
Positive a positions the circle right/above the origin; negative a positions it left/below.
Symmetry across the horizontal or vertical axis based on the sign.
Roses
Roses, represented as r=acos(kθ) or r=asin(kθ), have k determining the petal count.
Characteristics:
Odd k leads to k petals and even k results in 2k petals.
The angle between petals: 2π/k.
Symmetry across the horizontal or vertical axis.
Limacons
Limacons, given by r=a±bcosθ or r=a±bsinθ, have parameters a and b determining shape.
Shapes:
Dent (no loop) if ∣a∣>∣b∣.
Cardioid (heart shape) if ∣a∣=∣b∣.
Loop if ∣a∣<∣b∣.
Radius Characteristics:
Maximum radius:∣a∣+∣b∣.
Minimum radius: ∣a∣−∣b∣.
3.15: Rates of Change in Polar Functions
Characteristics of Polar Functions
Polar functions share similarities with other function types in analyzing characteristics like rate of change, increasing/decreasing intervals, positive/negative intervals, and extrema.
Polar Function Form: A polar function takes the form r=f(θ), where radii are output values and angles are input values.
Rate of Change: Positive, increasing, negative, and decreasing polar functions lead to an increasing distance from the origin (r).
Extrema: Transitions from increasing to decreasing or vice versa indicate relative extrema, representing points closest to or farthest from the origin.
Average Rate of Change: The average rate of change of r for θ over an interval is the ratio of the change in radius values to the change in θ. It signifies how the radius changes per radian.
Δr=(θ2)−f(θ1)/θ2−θ1f
Idea Summary
r positive: r positive, distance from origin increasing.
r negative: r negative, distance from origin decreasing.
r increasing: distance from origin increasing.
r decreasing: distance from origin decreasing.
Average rate of change formula: Δr/Δθ=f(θ2)−f(θ1)/θ2−θ1