AP Precalculus - Unit 1: Polynomial and Rational Functions Flashcards
Change in Tandem
Function: a mathematical relationship that maps a set of input values to a set of output values such that each input value is mapped to exactly one output value
Input Values = Domain = Independent Variable (x)
Output Values = Range = Dependent Variable (y)
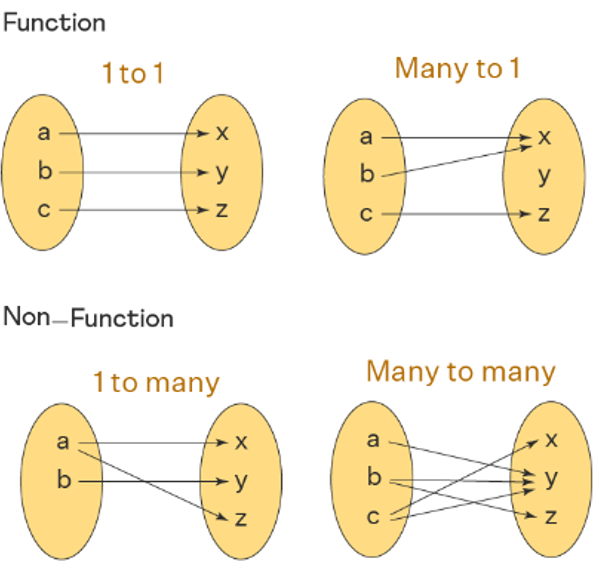
The input and output of a function vary according to the function rule
This can be represented graphically, verbally, analytically, or numerically
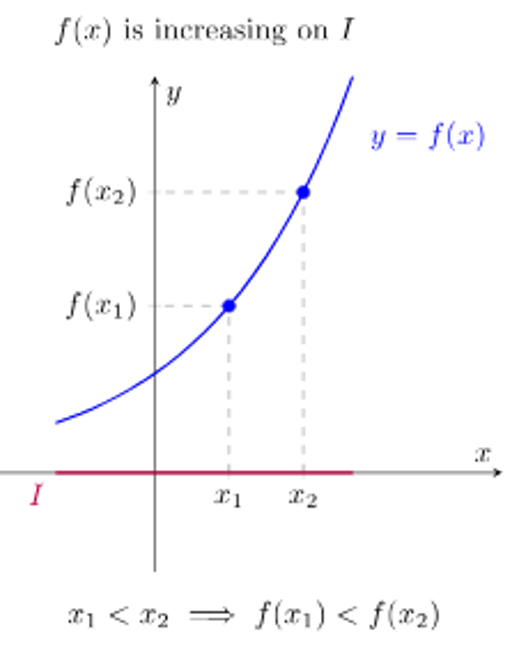
A function is increasing over an interval of its domain if:
as the input values increase, the output values always increase / for all a and b in the interval, if a < b, then f(a) < f(b)
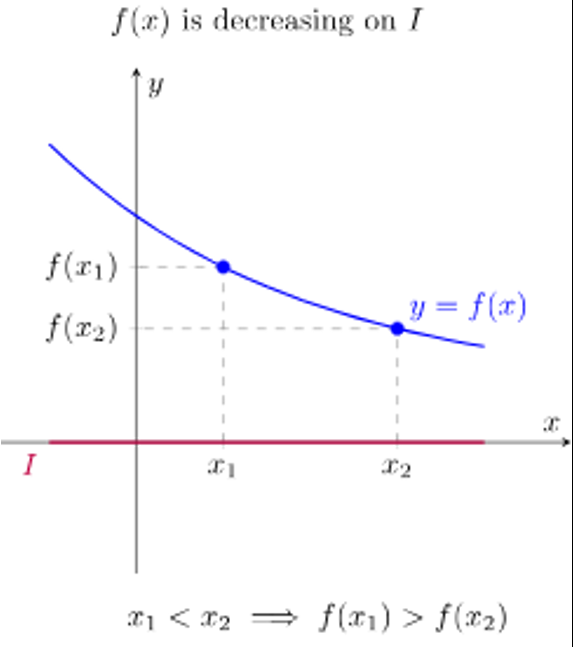
A function is decreasing over an interval of its domain if:
as the input values increase, the output values always decrease / for all a and b in the interval, if a < b, then f(a) > f(b)
Graph → a visual display of input-output pairs & shows how values vary
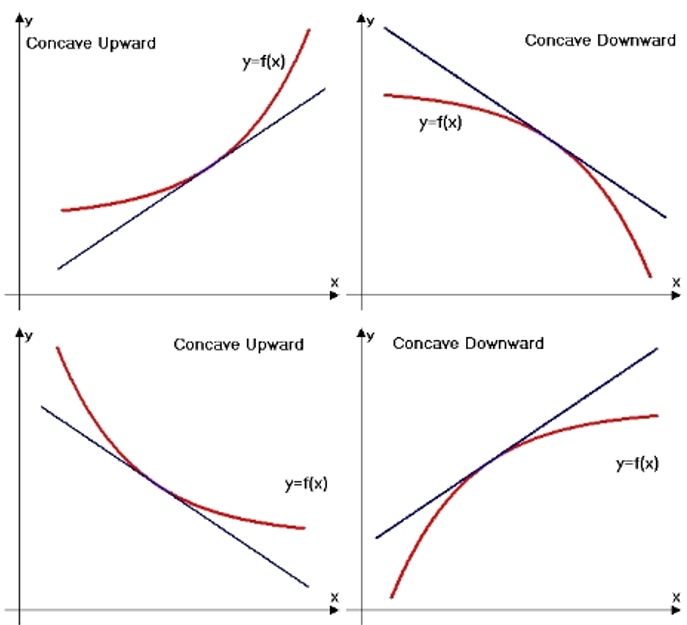
Concave up → a rate of change is increasing
Concave down → a rate of change decreasing
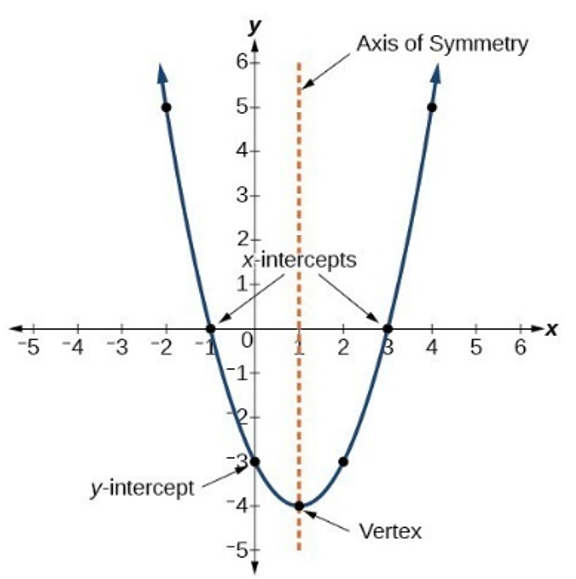
x-intercepts = zeros of the function
Rates of Change
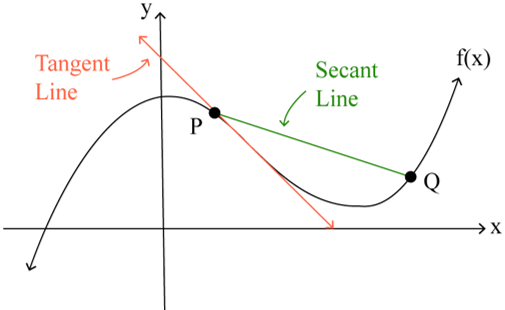
Average Rate of Change: The average rate of change over the closed interval [a, b] is the slope of the secant line from the point (a, f(a)) to (b, f(b))
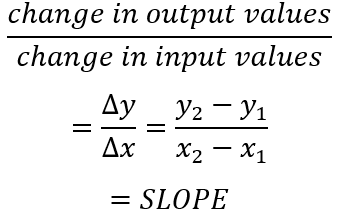
The Rate of Change of a Function at a Point → approximated by the average rate of change over small intervals containing the point
Positive Rate of Change → when one quantity increases, the other quantity increases as well
Negative Rate of Change → when one quantity increases, the other quantity decreases
AROC of Linear Function → constant
AROC changing at a rate of 0
AROC of Quadratic Function → slope of secant line (linear)
AROC changing at a constant rate
If AROC is increasing over interval → concave up
If AROC is decreasing over interval → concave down
Polynomial Functions
Polynomial Functions:
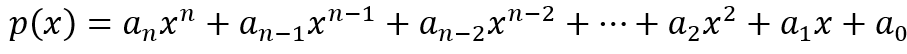
n = postitive integer polynomial degree = n
ai = a real number for each I from 1 to n leading term = anxn
an → nonzero leading coefficient = an
Local/Relative Maximum/Minimum: when polynomial changes between increasing and decreasing/included endpoint with restricted domain
Global/Absolute Maximum/Minimum: the greatest local maximum/least local minimum
Between two zeros of a polynomial → at least one extrema
Points of Inflection: when rate of change of function changes from increasing to decreasing or from decreasing to increasing; changes concavity
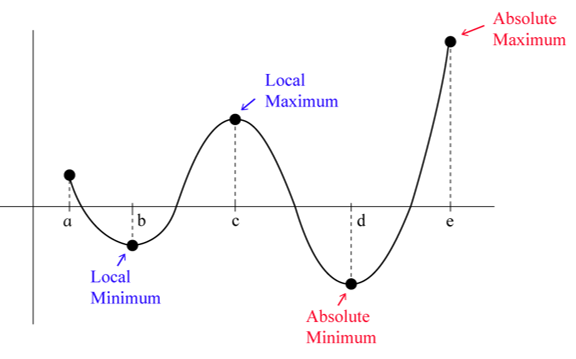
Polynomial with even degree → global maximum or global minimum
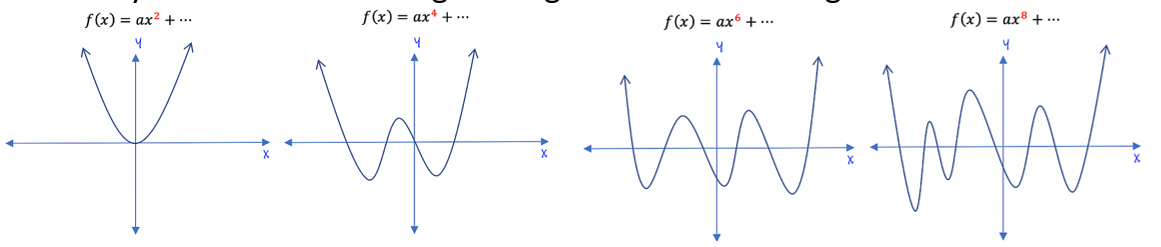
Complex Numbers: real numbers and non-real numbers
If p(a) = 0, then:
· a → zero/root of function p
· x-intercept at (a,0)
· if a is a real number, then (x – a) is a linear factor of function p
If linear factor (x – a) is repeated n times, then there are n zeros in the functions
└ a polynomial function of degree n has exactly n complex zeros
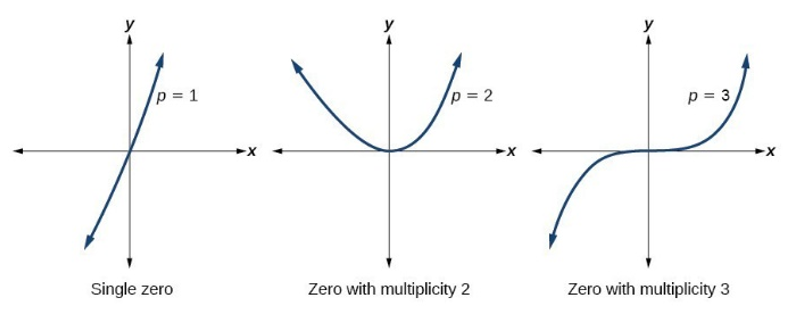
Real zeros of a polynomial can be endpoints for inequality intervals
If the real zero, a, has an even multiplicity (ex. (x – a)2), then the graph with “bounce” off the x-axis at x = a
Non-Real Zeros: if a + bi is a non-real zero of a polynomial p, then its conjugate a – bi is also a zero of polynomial p
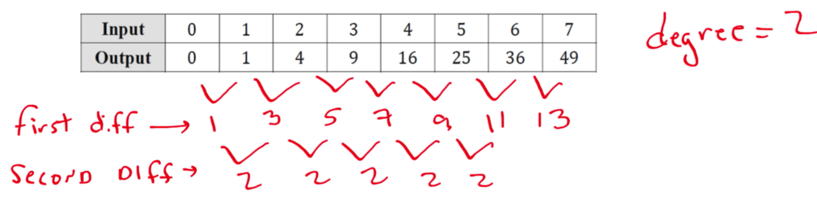
The degree of a polynomial function can be found by examining inputs and outputs of the function only if the input values are over equal intervals
└ The degree of the function = the least value of n for which the successive nth differences are constant
Graph of even function à symmetric over the line x = 0, f(-x) = x
Even function: when n is even in polynomial of the form p(x) = anxn*
Graph of odd function à symmetrix over the point (0, 0), f(-x) = - f(x)
Odd Function: when n is odd in polynomial of the form p(x) = anxn*
* where n ≥ 1 and an ≠ 0
End Behavior
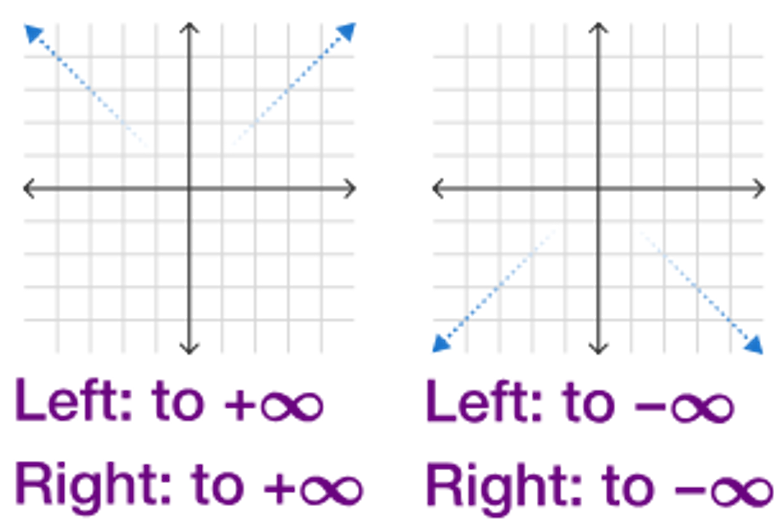
When input values of a function increase without bound, output values will either:
Increase without bound 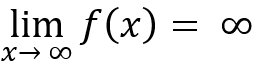
Decrease without bound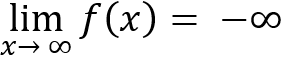
When input values of a function decrease without bound, output values will either:
Increase without bound
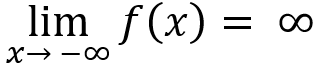
Decrease without bound
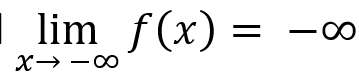
The degree and sign of the leading term of a polynomial determines the end behavior of the polynomial function
└ as input values increase/decrease without bound, the values of the leading term dominate
Rational Function
Rational Function: the ratio of two polynomials where the polynomial in the denominator ≠ 0
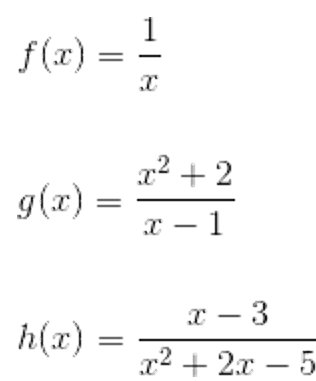
end behavior → affected by the polynomial of greater degree (values will dominate); can be understood by examining quotient of polynomial leading terms
ex.
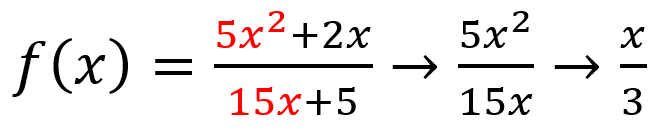 x grows as at a faster rate than 3, so function will go to ∞
x grows as at a faster rate than 3, so function will go to ∞
-if numerator dominates → quotient of leading terms is nonconstant polynomial à og function shares same end behavior
└ if leading term polynomial is linear → graph of rational function has slant asymptote parallel to the the graph of the line
-if denominator dominates → quotient of leading terms is (constant)/(nonconstant polynomial) à graph of og function has horizontal asymptote as y = 0
-if neither dominates → quotient of leading terms is constant = horizontal asymptote of og function
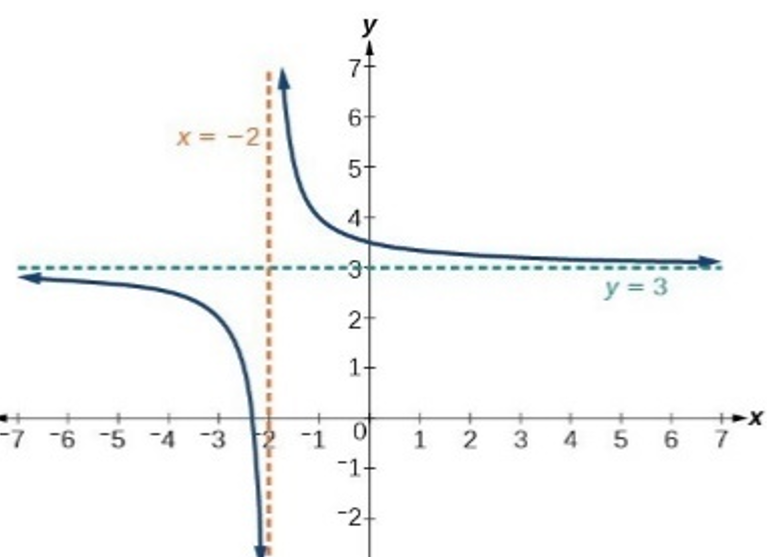
Rational Function Real Zeros → real zeros of the numerator in domain
└ real zeros of both polynomials in rational function are endpoints/asymptotes for intervals satisfying the inequalities r(x)≥ 0 or r(x) ≤ 0
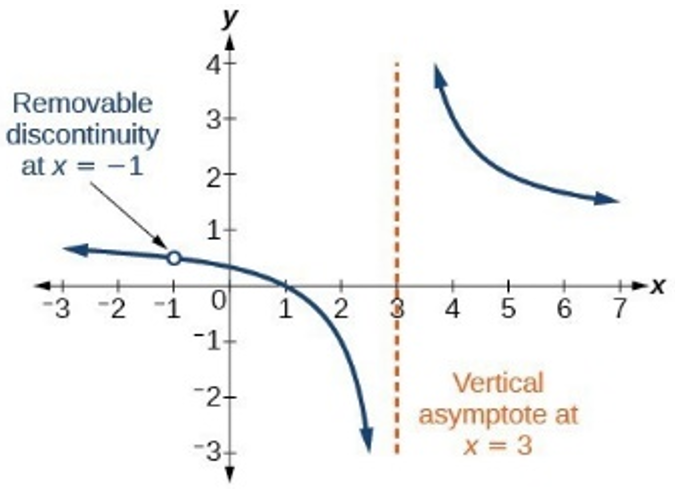
Vertical Asymptote → zeros of the polynomial in the denominator (and not numerator) / the zero appears more times in the denominator than in the numerator
Ex.
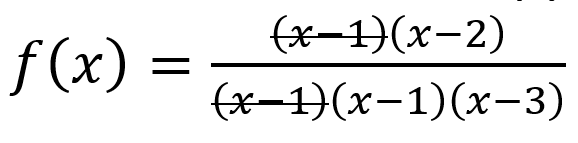 since (x – 1) appears more times in the denominator, it would be a vertical asymptote
since (x – 1) appears more times in the denominator, it would be a vertical asymptote
If input values are greater than asymptote, then
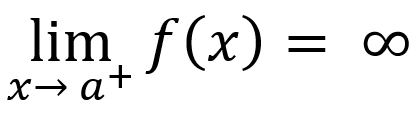 or
or
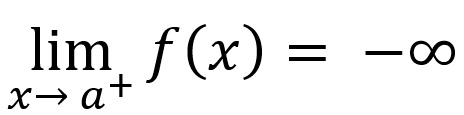
If input values are less than asymptote, then
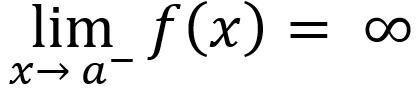 or
or
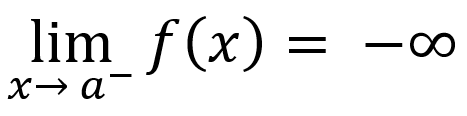
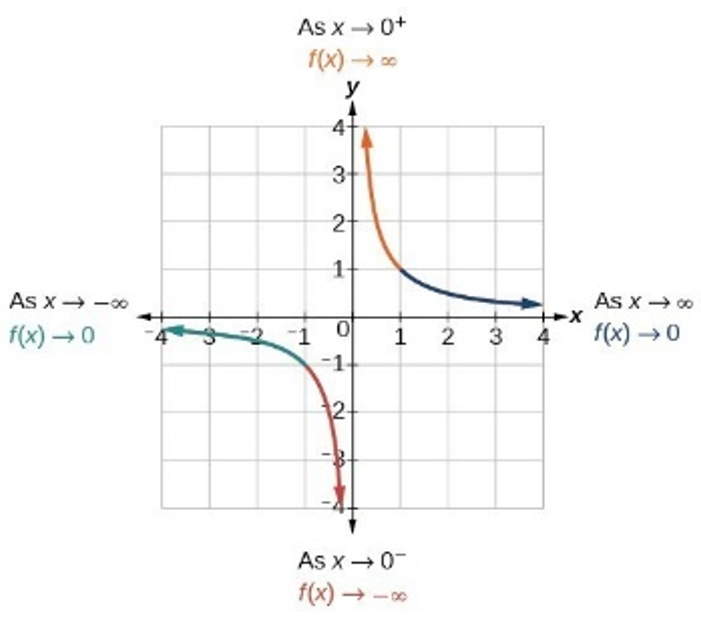
Hole → when a zero appears more times in the numerator than the denominator
-Find the location of the hole by plugging in zero value into function
Equivalent Representations of Polynomial and Rational Expressions
standard form of polynomial and rational functions à used to find end behavior
factored form of polynomial and rational functions à used to find x-intercepts, asymptotes, holes, domain, and range
Polynomial Long Division à used to find equations of slant asymptotes of graphs of rational functions
└ degree of remainder is less that degree of divider
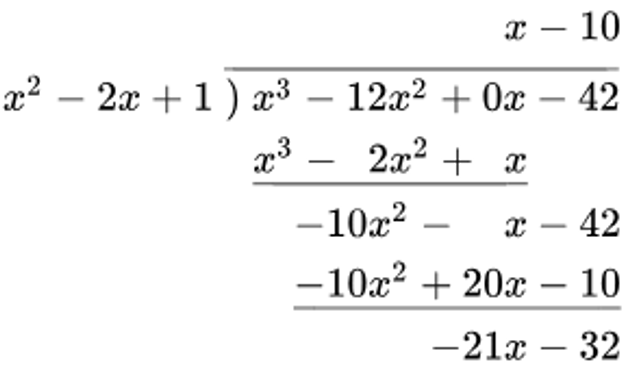
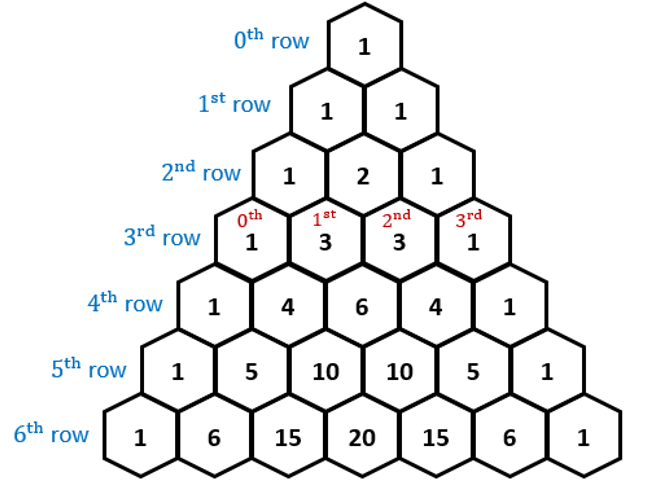
Binomial Theorem → used to expand terms in the form (a + b)n and polynomials functions in the form of (x + c)n (where c is a constant) by using Pascal’s Triangle
Ex.
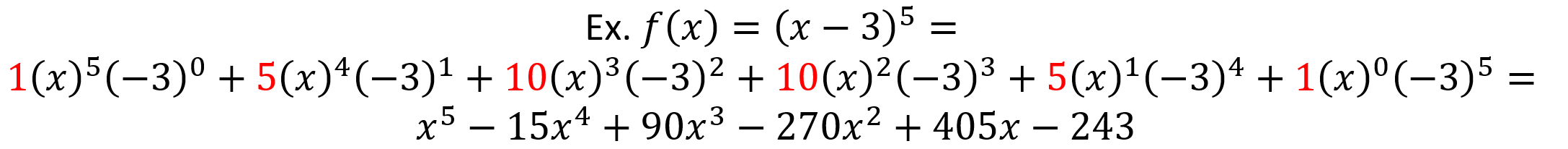
Pascal’s Triangle:
Transformations of Functions
Functions can be transformed from parent function f(x)
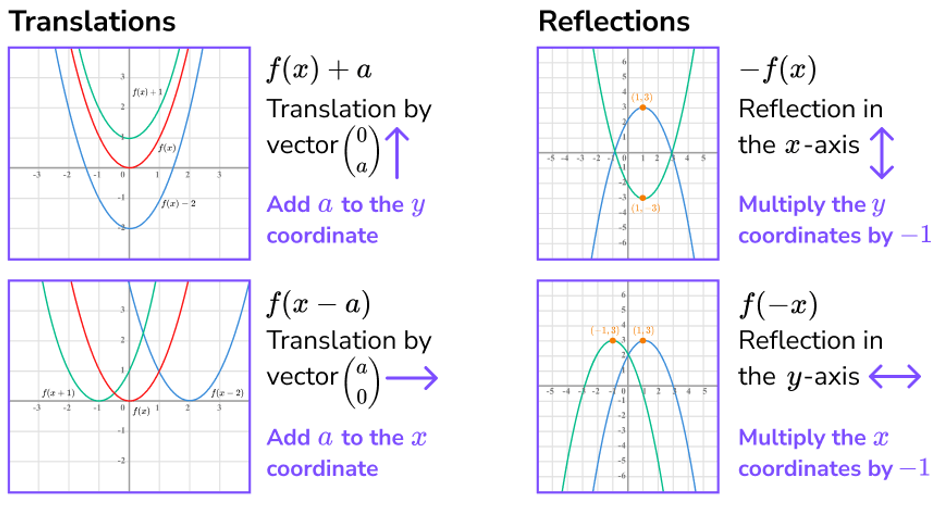
g(x) = f(x) + k → vertical transformation of f(x) by k units
g(x) = f(x + h) → horizontal transformation of f(x) by -h units
g(x) = a f(x), where a ≠ 0 → vertical dilation by a factor of |a|;
if a < 0 → reflection over the x-axis
g(x) = f(bx), where b ≠ 0 → horizontal dilation by a factor of | |, if b < 0 → reflection over y-axis
*The domain and range of a transformed function may differ from the parent function
Function Model Selection and Assumption Articulation
Linear Functions → used for contextual scenarios with roughly constant rates of change
Quadratic Functions → used for contextual scenarios with roughly linear rates of change/ roughly symmetrical data sets with a unique minimum/maximum value
Geometric → used for contextual scenarios involving area/volume; two dimensions modeled by quadratic functions, three dimensions modeled by cubic functions.
Polynomial → used to model data sets/scenarios with multiple zeros or multiple extremas
Piece-wise → a set of functions defined over nonoverlapping domain interval; used for data sets/contextual scenarios that have different characteristics over different intervals
Assumptions and Restrictions of Function Model
a model may:
-assume what is consistent
-how quantities change together
-require domain restrictions (based on mathematical clues, context clues and/or extreme values)
-require range restrictions (ex. rounding values) (based on mathematical clues, context clues and/or extreme values)
Function Model Construction and Application
A model can be constructed in multiple ways:
- based on restrictions from a scenario
- using transformations from the parent function
- technology and regressions (linear, quadratic, cubic, & quartic)
- a piece-wise function can be constructed through a combination of the techniques above
Data sets that have quantities that are inversely proportional → rational functions
Ex.
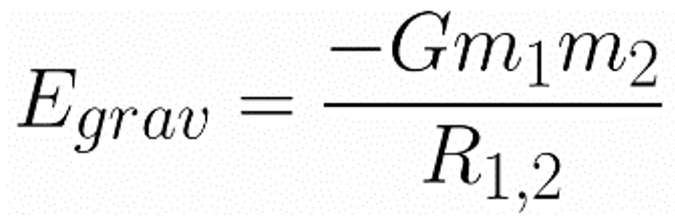
Application:
Models can be used to draw conclusions about the data set/scenario
Appropriate units of measure should be used when given