y9 maths
#75CA56 - green
TOPIC 1: PROBABILITY
W1AB: Probability Basic Principles:
Probability tells us how likely something is to happen.
The highest probability of an event happening is 1
The lowest probability of an event happening is 0
Probability should be stated as a fraction (or a decimal if it is exact)
Do NOT state a probability as a percentage, unless the question calls for it.
e.g. 1/2 can be written as 0.5, but 1/3 can’t, since it is 0.333…
OUTCOME: one possible result of an experiment
e.g. the outcome of rolling a dice is 5
SAMPLE SPACE: the possible outcomes of an experiment
e.g. for rolling a dice, the sample space is {1, 2, 3, 4, 5, 6}
Pr(event) = number of outcomes the event occurs/total number of outcomes
All probabilities of outcomes will add up to 1.
COMPLEMENTARY EVENTS: two events which have probabilities that add up to 1. A complementary event of an event is marked with Pr(Event’).
e.g. the probability of getting a red jellybean in a bag of jellybeans is 1/3, or Pr(R). The probability of getting any other color is Pr(R’).
EXPERIMENTAL PROBABILITY: When you can’t find the theoretical probability of an event happening, you can use experimental probability.
experimental probability = number of times the event occurs/number of trials in the experiment.
The more trials an experiment has, the more accurate the experimental probability is likely to be.
EXPECTED NUMBER OF SUCCESS: The number of times an outcome is expected to occur
e.g. to roll a 6 in a dice, there is a 1/6 chance. If there are 60 trials, the dice is expected to land on 6 10 times.
expected number of success = probability of success x number of trials.
W2AB & W3AB: Venn Diagrams and Karnaugh Maps:
UNION: The union of A and B in a Venn diagram, which includes A, B and whatever’s in both.
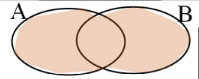
INTERSECTION: The intersection of A and B, which includes everything in A and B.
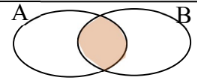
A’ is the compliment of A, which includes anything that is NOT A. This includes things that are both A and B.
KARNAUGH MAPS: Also known as a two-way table, this is another way to present the information from a Venn diagram.
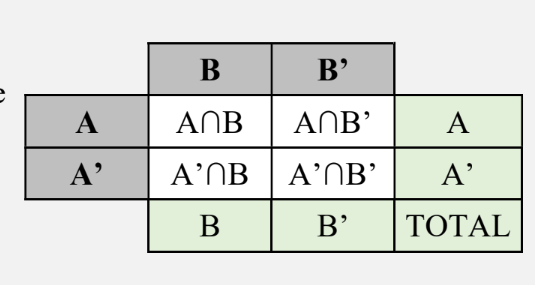
If a question asks for Pr(A and B), it means Pr(A∩B).
If a question asks for Pr(A or B), it means Pr(AUB)
W4AB: Probability and Algebra:
THE ADDITION RULE:
n(AUB) = n(A) + n(B) - n(A∩B)
Pr(AUB) = Pr(A) + Pr(B) - Pr(A∩B)
This rule can be rearranged to find other parts of the equation, such as Pr(A) or Pr(B).
W5AB: Using Tables:
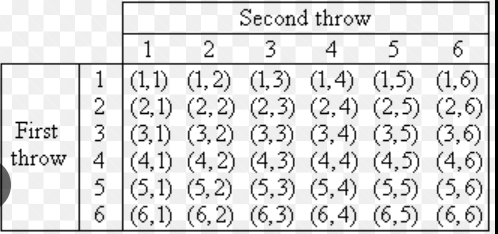
WITH REPLACEMENT: write all possible outcomes on the table.
e.g. if 6 balls labelled 1-6 are put in a bag, and ne is taken out with replacement, both balls can be a 6.
WITHOUT REPLACEMENT: write all possible outcomes and cross out the ones that repeat.
e.g. 6,6 cannot be possible if two balls labelled 1-6 are selected from a bag without replacement.

W6AB and W7AB: Tree Diagrams:
Tree diagrams can be used for experiments with more than one stage.
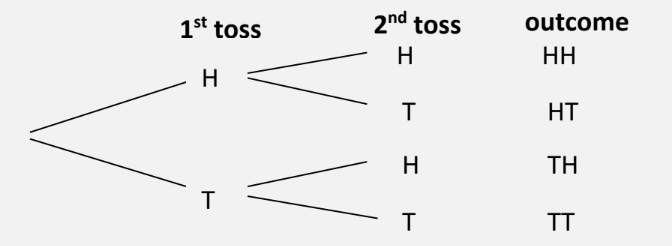
There are two types of tree diagrams:
Type 1: all outcomes are showed separately. This would not be suitable for scenarios where there are more than one of the same item.
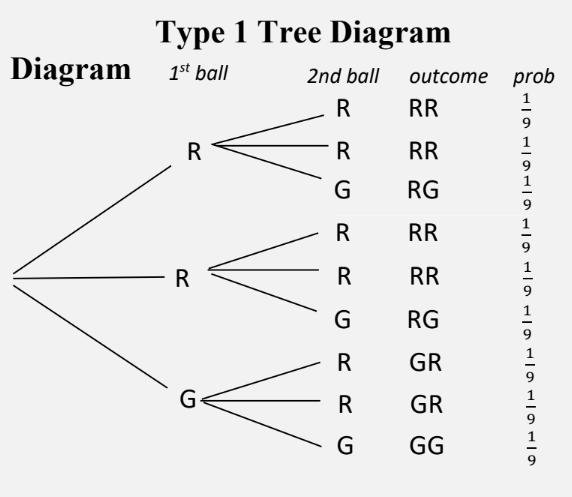
In this one, there are all possible outcomes, with some repeating, and all of them have a 1/9 chance of occurring.
Type 2: there is only one branch for one outcome, and the probability is written next to it. This is more effective for larger sets of items.
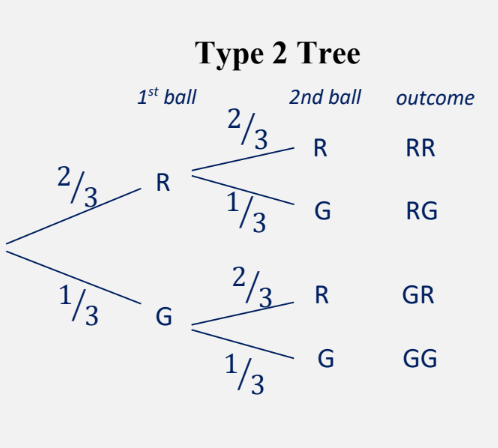
In this tree diagram, there is only one of each possible outcome, with probabilities next to the branches. This can help us to find the probability by multiplying the probabilities of both stages.
e.g. the probability of getting both red balls = 2/3 × 2/3 = 4/9.
If you need to calculate the probabilities of getting either both red balls or both green balls, you need to add Pr(RR) and Pr(GG).
Without replacement: If a tree diagram needs to be shown for a scenario without replacement, you need to subtract the removed object from the probability in the next stage.
e.g. if the probability of getting a red ball is 6/11, and a red ball is taken out, the probability of getting a red ball in stage 2 will be 5/10, since there are only 5 red balls left, and 10 balls in total.
SAME AND DIFFERENT PROBABILITIES:
Scenario: Chelsea has a bag of lollypops, 6 or which are red and 5 of which are green. Chelsea chooses a lollypop and gives it to Clarissa. She then chooses a second lollypop for herself.
For same probabilities (e.g. Pr(RR) + Pr(GG)), you can add the probabilities.
For different probabilities, there are two methods.
Method 1: Pr(Different) = 1 - Pr(same)
Method 2: Pr(Different) = Pr(RG) + Pr(Gr)
W8AB: Multiplying to Calculate Probabilities:
TIP: Instead of drawing a tree diagram for finding a probability, you can also just multiply the known probabilities together.
e.g. 3 red balls and 4 green balls, both balls are green.
4/7 × 4/7 = 16/49
IMPORTANT: There can also be questions, where a specific item is selected during the first stage, while another specific item is selected during the second stage.
e.g. a black sock first, then a white sock.
For finding different probabilities, you need to find how many ways the scenario can happen.
e.g. tossing two tails and a head in a coin
there are three ways this can happen; TTH, THT, and HTT.
TOPIC 2: ALGEBRA
W1AB: Algebra, Solving Equations, Square Roots:
Terminology:
Equation: an equation tells us that two things are equal.
e.g. 2x = 6
Expression: an expression does not have an equal sign.
e.g. 5x+3
Pronumeral/Variable: a letter or symbol used to represent numbers
e.g. x, y
Coefficient: a number that multiplies a pronumeral
e.g. in 2x, 2 is the coefficient.
Constant: the part of an equation that is just a number.
e.g. in 2x+2, 2 is the constant.
Like terms: two or more terms that have the same pronumerals (and powers)
Evaluate: find the value of an expression. It has to be a number.
Squaring negative numbers: (-2)² = -2 x -2
ORDER OF OPERATIONS = BODMAS
Expanding brackets:
e.g. 2+5(3x-2)
Multiply everything in the bracket by 5
= 2+15x-10
= 15x-8
Solving equations: you can add, subtract, multiply and divide the same number from both sides of the equation.
e.g. 4x-5=2
Add 5 to each side
= 4x = 7
= x=7/4
W2AB and W3AB: Linear Equations and Inequalities:
Greater than or lesser than?
e.g. 2<7, this shows that 2 is less than 7, or 7 is greater than 2.
Crocodile method: The crocodile always eats the bigger number, so the inequality sign’s wider end should face the bigger number.

Plotting inequalities on a number line:
Use an open circle for < and >
Use a closed circle for ≤ and ≥
Examples:

Solving inequalities: This is very similar to solving equations, but you need to flip the sign when you divide or multiply by a negative number.
e.g. 3x-1 < 5
Solve it just like you would solve 3x-1=5
3x < 6
x < 2
e.g. −3x > 12
Since you divide both sides by -3, you need to turn the inequality sign around.
x < 12/-3
x < -4
Integers satisfying two inequalities: To do this, you need to solve both inequalities individually, and see which integers satisfy both.
e.g. x − 2 > 4 and 3x < 30
x > 6 and x < 10
Find numbers that are more than 6, but less than 10.
x = 7, 8, 9
“3-part” inequalities: These can be solved the same way as simple inequalities.
e.g. -8 < 2x < 10
Divide all of them by 2
-4 < x < 5
e.g. −6 < −3x < 9
Since you are dividing by -3, you need to flip the signs around.
2 > x > -3
The final expression needs to be written with the lower numbers on the left.
-3 < x < 2
W4AB: More Solving Equations:
Solving equations with number/pronumeral:
e.g. 4/x + 5 = 7
= 4/x = 2
Multiply both sides by x
= 4 = 2x
x = 2
Solving equations with fractions:
e.g. 2x-1/2 = x+4/5
Method 1: common denominator
5(2x-1)/10 = 2(x+4)/10
10x-5/10 = 2x+8/10
Multiply both sides by 10
10x-5 = 2x+8
8x = 13
x = 13/8
Method 2: cross multiply:
5(2x − 1) = 2(x + 4)
10x − 5 = 2x + 8
A shortcut for method 1
W5AB and W6AB: Transposing Formulae:
Subject: A pronumeral on it’s own on the LHS of an equation
Transposing: Changing the subject of an equation by moving the terms around
e.g. y = w/4+3x (make w the subject)
y-3x = w/4
w = 4(y-3x)
Transposing with factorisation:
e.g. xw = y-5x (x)
xw + 5x = y
x (w+5) = y
x = y/w+5
Transposing with square roots: You need to square all the terms in the equation
e.g. \sqrt{x} −w = a (x)
\sqrt{x} = a+w
Square everything
x = (a+w)²
Square roots: When taking a square root you must always consider whether to include both the positive and negative square roots.
e.g. x² = 25
x = 土5
When you solve a math question related to something that can only be measured in positive numbers (e.g. length, time, weight), you must have a positive answer.
If there is a fraction in the question, multiply all the terms in the equation by the denominator of the fraction.
W7AB: Solving Simultaneous Equations by Substitution
Solving Simultaneous Equations by Substitution:
e.g. y = 3x−4 (1) y = x+6 (2)
Since both these equations equal y, you can put them into an expression like so:
3x-4 = x+6
2x = 10
x = 5
Substitute x into one of the equations:
y = 15-4
y = 11
x = 5, y = 11
e.g. y = 2x+4 and 2y−3x = 5
Substitute y into the other equation
2(2x+4)-3x = 5
4x+8-3x = 5
x+8 = 5
x = -3
For worded questions, you need to define the pronumerals used before solving.
W8AB: Simultaneous Equations by Elimination:
When solving simultaneous equations we begin by forming an equation that only contains one unknown (either just x or just y). Sometimes it is not easy to use substitution to do this, instead we can use a process called “elimination”. The aim is to eliminate (get rid of) either all the x’s or all the y’s.
e.g. 2x+y = 13 (1)
3x−y = 12 (2)
Add these two equations together to eliminate y
5x = 25
x = 5
Substitute into one of the equations
15-y = 12
-y = -3
y = 3
For some equations, you need to multiply them by a specific number or pronumeral, so that you can eliminate a term.
e.g. 2x + 3y = 13
3x − y = 3
TOPIC 3: PYTHAGORAS, SURDS AND INDICES
W1AB: Working with Surds:
Surds: numbers that can only be represented as a square root (e.g. \sqrt2, \sqrt7 )
Operations with surds: 3\sqrt2 = 3 x \sqrt2
Adding and subtracting - You can add and subtract ‘like surds’ (e.g. 3\sqrt2 and 5\sqrt2 )
e.g. 3\sqrt2 + 5\sqrt2 = 8\sqrt2
Multiplying surds - Multiply the values inside the square roots
e.g. \sqrt{20} x \sqrt2 = \sqrt{40}
To multiply expressions such as 2\sqrt3 x 6\sqrt5 , you need to multiply the integers, and then the surds.
so 2\sqrt3 x 6\sqrt5 = 12\sqrt{15}
Dividing surds - \frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}
e.g. \frac{\sqrt{10}}{\sqrt2}=\sqrt{\frac{10}{2}}
Simplifying Surds: To simplify surds, you need to split them into factors, where one of them has to be a perfect square. Then, you can take it out of the surd, and put it as an integer next to the surd.
e.g. \sqrt{18} = 3\sqrt2
\sqrt{18}=\sqrt{9\cdot2}
3\sqrt2
If there is more than one factor that is a perfect square, then you need to use the larger one, so that simplifying is more simple.
Expressing surds as a square root of a positive integer: You need to square the integer, put it in a square root symbol, and multiply it with the surd.
e.g. 3\sqrt5 = \sqrt9\cdot\sqrt5 = \sqrt{45}
Types of numbers:
Real numbers(R) - All numbers on the number line are considered ‘real’ numbers
Rational numbers (Q) - All fractions which have an integer as both the numerator and the denominator
Any number with a recurring decimal is considered irrational.
Integers (Z) - All whole numbers that are either positive or negative
Natural numbers - Numbers used for counting
Squaring expressions: For squaring surds, you need to square the integer first and then the surd itself. The answer will be an integer most of the time.
W2AB: Pythagoras’ Theorem:
Exact value - The value must not be rounded off. It must be given as surds or fractions where necessary. If a question doesn’t specifically ask for a rounded off value then you should give an exact value
Square root - For square rooting, you need to consider that it might be positive or negative.
Squaring - Brackets make a huge difference. 3x² is different to (3x)². 3x² equals 3x², while (3x)² is equal to 9x².
If you are solving a question related to the shape or quantity of something (e.g. length, time, height), you must take the positive answer from the square root, since negative answers are infeasible. For this, you always need to write the explanation.
Hypotenuse and Pythagoras’ Theorem: The Hypotenuse is the longest side of a right-angled triangle, which is always opposite the right angle.
Pythagoras’ Theorem: c^2=a^2+b^{^2}
You can substitute the values of the two other sides into a and b, to find c, or you can substitute the values of any variables to find any side.
W3AB and W4AB: Further Surds and Pythagoras’ Theorem:
Estimating the value of surds: Find surds with perfect squares that are closest to the surd, and you have an estimate.
e.g. \sqrt{11}
\sqrt9<\sqrt{11}<\sqrt{16}
so 3<\sqrt{11}<4
Formula for cubes of surds = (\sqrt{a} )³ = a\sqrt{a}
If the side lengths of a right-angled triangle satisfy Pythagoras’ Theorem, then you know it’s a right-angle triangle.
W5AB: Index Laws:
Law 1: am x an = am+n
Law 2: am/an = am-n
Law 3: (xm)n = xmn
Law 4: a0 = 1
Law 5: (ab)m = ambm
Law 6: (a/b)m = am/bm
W6AB: Indicial Equations:
Multiplying decimals:
e.g. 0.2 × 0.3
Multiply the numbers as if they weren’t decimals
2 × 3 = 6
Divide the number by the total amount of decimal places in both numbers
0.2 × 0.3 = 0.06
Solving indicial equations:
e.g. 3x = 9
3x = 3²
x = 2
e.g. 1000x+2 = 10000
(103)x+2 = 104
103x-6 = 104
3x-6 = 4
3x = 10
x = 10/3
W7AB: Negative indices:
a-n = 1/an
e.g. 2x = 1/16
2x = 1/24
2x = 2-4
x = -4
TOPIC 4: QUADRATIC ALGEBRA
W1AB: Factorising:
Factorising:
e.g.1 6a+ax
The common factor is a. Take a out from the expression’s terms.
= a(6+x)
e.g.2 6(x-2) + x(x-2)
(x-2) is the common factor.
= (6+x)(x-2)
e.g.3 3x(x−1) + 2(−1+x)
(-1+x) = (x-1)
= (3x+2)(x-1)
e.g.4 x(x−3) + x−3
x-3 on its own is multiplied by 1.
= (x+1)(x-3)
e.g.5 x(x−3) + 4(3−x)
Notice how (x-3) and (3-x) are not the same. Take -1 out as a common factor from the second bracket.
= x(x−3) − 4(−3+x)
= x(x−3) − 4(x−3)
= (x−3)(x−4)
Factorising by grouping:
e.g. 4x²−8x − 3x+6
= 4x(x−2) − 3(x−2)
= (x−2)(4x−3)
Factorising quadratic trinomials:
For Factorising expressions with the form x²+bx+c, you need to find factors of c that add to b.
Case 1: When c and b are positive, both factors are positive.
e.g. x²+8x+12
Factors of 12 that add to 8 = 2, 6
= x²+2x+6x+12
= x(x+2)+6(x+2)
= (x+2)(x+6)
SHORTCUT METHOD:
Factors of 12 that add to 8 = 2, 6
= (x+2)(x+6)
Case 2: When c is positive and b is negative, both factors are negative.
e.g. x²−10x+16
Factors of 16 that add to -10 = -8, -2
= x²-2x-8x+16
= x(x-2)-8(x-2)
= (x-8)(x-2)
SHORTCUT METHOD:
Factors of 16 that add to -10 = -8, -2
= (x-8)(x-2)
Case 3: When c is negative, use one negative factor.
e.g. x²+4x−12
Factors of -12 that add to 4 = -2, 6
= x²-2x+6x-12
= x(x-2)+6(x-2)
= (x+6)(x-2)
SHORTCUT METHOD:
Factors of -12 that add to 4 = -2, 6
=(x-2)(x+6)
Perfect squares:
a²+ 2ab + b² = (a + b)²
a²− 2ab + b² = (a − b)²
e.g. x²+8x+16
Using the rule, find the factors.
= x²+2(4)x+4²
a = x, b = 2
= (x+2)²
W2AB: More Factorising:
Common factors: Some expressions have common factors for all terms. If the coefficient of x is -1, take out -1 as a factor.
e.g. 2x²+12x+16
Take out 2 as a common factor
= 2(x²+6x+8)
= 2(x²+2x+4x+8)
= 2(x(x+2)4(x+2))
= 2(x+4)(x+2)
Difference of perfect squares (DOPS): (a-b)(a+b) = a²-b²
e.g. x²-9
Use the DOPS rule to find the factors.
= (x-3)(x+3)
DOPS Factorising using fractions:
e.g. x²-1/16
= x²-(1/4)²
= (x-1/4)(x+1/4)
Factorising without expanding:
e.g. (x+4)²-9
= (x+4)²-3²
= (x+4+3)(x+4-3)
= (x+7)(x+1)
W3AB: Factorising Non-Monic Quadratics:
Factorising ax²+bx+c:
e.g. 6x²+17x+5
a = 6, b = 17, c = 5
Find factors of ac that add to b = 15, 2
= 6x²+2x+15x+5
= 2x(3x+1)+5(3x+1)
= (2x+5)(3x-1)
Before factorising, find common factors for all terms in the expression.
W4AB and W5AB: Solving Quadratic Equations:
Null Factor Law: Everything multiplied by 0 is equal to 0. For the answer of an equation to be 0, one of the numbers/expressions must equal 0.
e.g. if ab = 0, then a, or b, or both must be 0.
NULL FACTOR LAW: if ab = 0, then a = 0 or b = 0
e.g.1. x(x-5) = 0
Either x = 0 or x = 5
e.g.2 4(x+1)(x-7) = 0
Divide both sides by 4. Remember, 0/4 = 0
(x+1)(x+7) = 0
x = -1 or x = 7
e.g.3 x²+6x+8 = 0
(x+2)(x+4) = 0
x = -4, -2
e.g.4 x²-x = 20
Make the equation equal to 0 by moving 20 to the LHS
x²+x-20 = 0
(x+5)(x-4) = 0
x = -5, 4
e.g.5 2x²+10x+12 = 0
Take out 2 as a common factor
2(x²+5x+6) = 0
2(x+3)(x+2) = 0
Ignore the 2
x = -3, -2
You can also divide the equation by 2 at the beginning.
If the common factor is -1, you need to divide by -1 at the beginning.
For finding x for expressions such as 3x-2, you need to bring the 2 to the other side (3x = 2), and then divide the 2 by 3 (x = 3/2).
W6AB: Forming and Solving Quadratic Equations:
e.g. a) Write down an expression, in terms of x, for the area of this rectangle:
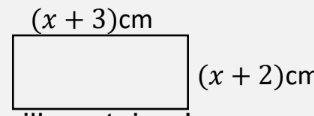
(x+3)(x+2) ← no need to expand now
b) If the area of the rectangle is 20cm², form an equation and solve it to find the value of x.
(x+3)(x+2) = 20
Expand the expression now
x²+5x+6 = 20
x²+5x-14 = 0
(x+7)(x-2) = 0
x = -7,2
Remember that things such as time, distance and speed don’t have a negative value, so the only option that you can choose here is x = 2. Don’t forget to cross out the other answer and put ‘infeasible’ next to it.
Methods to eliminating answers:
Method 1: Recommended
Cross out the infeasible answer, and put ‘infeasible’ next to it. You should put both answers initially.
e.g. x = 2, x = -7 infeasible
x = 2
Method 2:
Put the reason why a value is infeasible in the second last step, then write the answer.
e.g. x² = 36, x>0
x = 6
Method 1 is recommended, since you don’t have to list the reason, and it prevents the chance of giving the wrong reason.
TOPIC 5: MEASUREMENT
W1AB: CAS Skills Part 1
Simple calculations:
Click the grey calculator icon to create a new document. Then, just type the expression you want to solve, and solve it.
Solving equations with a CAS:
To solve equations on the CAS,
Press ‘menu’
Press ‘3: Algebra’
Press ‘1: Solve’
Type the equation in the bracket, and put a comma, then the pronumeral to solve for next to it.
e.g. solve(x+2=5,x)
NOTE: you can also type ‘solve’ in the calculator, but this might take a long time, since the keyboard layout is not QWERTY.
Solving inequalities on the CAS:
To solve inequalities, do the same thing that you would do for equations, but use the inequality signs (ctrl + =)
e.g. solve(9–2*x<25,x)
NOTE: you need to put 2*x if you want to do 2x in the CAS.
W2AB: Length, Perimeter and Circumference
If units are in the question, you MUST put them in the answer. You don’t have to include units if the unit isn’t specified.
PERIMETER OF A CIRCLE = 2πr or πd (r = radius, d = diameter).
SECTORS: A sector is a fraction of a circle. The fraction can be found by θ/360 (θ = angle of the sector)
PERIMETER OF A SECTOR: θ/360 × πd + 2r
NOTE: if the question doesn’t specify the number of decimal places the final answer needs to be rounded off, then put the answer in terms of pi.
W3AB: Area of 2D shapes:
AREA OF A TRIANGLE = 1/2 x b x h (b = base, h = height)
AREA OF A SQUARE = l² (l = length)
AREA OF A CIRCLE = πr² (r = radius)
AREA OF A RECTANGLE = l x w (l = length, w = width)
AREA OF A TRAPEZIUM = 1/2 (a+b)h (a = top length, b = bottom length, h = height)
AREA OF A KITE/RHOMBUS = xy/2 (x = horizontal length, y = vertical length)
AREA OF A PARALLELOGRAM: = b x h (b = base, h = height)
Composite shapes:
To find areas of composite shapes, you need to break them down into simpler shapes, and find the area of the shapes.
W4AB: Total Surface Area
Total surface area:
The total surface area of a 3D shape can be found by adding up the area of all the sides of the shape.
TSA of a cuboid = 2(wl)+2(wh)+2(lh)
TSA of a cylinder = 2πr²+2πrh
TSA of a cube = 6l²
Composite solids:
Composite solids are basically like composite shapes, but with 3D shapes. You find the total surface area of them by eliminating common faces.
e.g. if there is a cylinder on top of a cuboid, you have to subtract the area of the circular face of the cylinder from the area of the top face of the cuboid.
W5AB: Volume of Prisms and Cylinders
What are prisms?
Prisms are solids that have a constant cross section
AREA OF A PRISM = cross section x length
What are cylinders?
Cylinders are solids with a constant circular cross section.
AREA OF A CYLINDER = same as area of a prism
What is a cross section?
A cross section is a two-dimensional shape that results from cutting a solid.
Why is it important for us to identify the cross-section before calculating the volume of prisms and cylinders?
Finding the cross section is important, because finding the area of it will help find the volume of the prism/cylinder.
Do pyramids have a cross section?
No, it does not, since the cross-section is inconsistent.
VOLUME OF A PRISM = cross section x height
VOLUME OF A CYLINDER = πr²h (r = radius)
W6AB: Unit Conversions
Linear unit conversions:
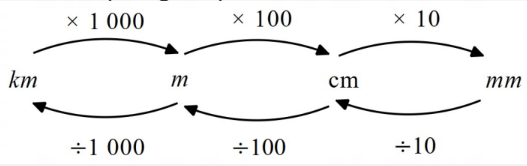
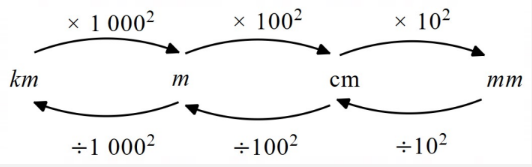
Square unit (area) conversions:
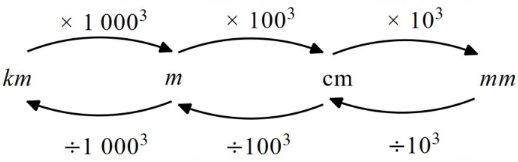
Cubic units (volume) conversions:
Liquid conversion:
1cm³ = 1mL
1m³ = 1kL
W7AB: CAS skills Part 2
Factorising with the CAS:
To factorise an expression, you need to do the following steps:
Click ‘menu’, then ‘3: Algebra’ and ‘2: Factorise’
Put the expression in the brackets, followed by ‘,x’
Press ‘enter’
NOTE: The function won’t work if you don’t put ‘,x’ next to the expression.
You can also type out ‘factor’, but it will take a while.
Expanding with the CAS:
To expand an expression, you need to do the following steps:
Click ‘menu’, then ‘3: Algebra’ and ‘3: Expand’
Put the expression in the brackets
NOTE: You need to put * between each bracket
W8AB: Transposing Formulae
Transposing with a CAS:
To transpose an equation, use the solve function, and the pronumeral that you need to make the subject next to the comma.
e.g. d = s*t (make s the subject)
solve(d=s*t,s)
UNIT 6: LINEAR GRAPHING AND EQUATIONS
QUESTIONS:
What is a Cartesian Plane?
A cartesian plane is a graph, with positive and negative coordinates. The x and y axes form quadrants.
What are coordinates?
Coordinates are the point of a Cartesian Plane, labelled as (x, y).
Can you tell the difference between linear and non-linear relationships?
Linear relationships are straight lines, and the exponent of x is 1. Non-linear involves lines that have other numbers as an exponent of x, such as 2 (e.g. parabolas)
What are the x and y intercepts?
The x and y intercepts are the points on the x and y axis that a line crosses over at.
W1AB: LINEAR RELATIONS PART 1
Linear relations:
There are many different rules used to describe relationships between x and y values.