1.4.2 data structures

array

ordered, finite set of elements of a single type

one dimensional array

• a 1D array is a linear array

• arrays are always taken to be zero-indexed

• this means that the first element in the array is considered to be at position zero

two dimensional array

• a two-dimensional array can be visualised as a table or spreadsheet

• when searching through a 2D array, you first go down the rows and then across the columns to find a given position

• this is the reverse to the method used to find a set of coordinates

three dimensional array

• a three-dimensional array can be visualised as a multi-page spreadsheet and can be thought of as multiple 2D arrays

• selecting an element in a 3D array requires the following syntax to be used: threeDimensionalArray[z,y,x]​, where z is the array number, y is the row number and x is the column number

records

• a collection of related data fields that represent a single item or entity in a database, typically structured in rows within a table

• referred to as a row in a file

• made up of fields, and is widely used in databases

lists

• a data structure consisting of a number of ordered items where the items can occur more than once

• Lists are similar to 1D arrays and elements can be accessed in the same way

• list values are stored non-contiguously

• this means they do not have to be stored next to each other in memory, as data in arrays is stored

• lists can also contain elements of more than one data type, unlike arrays

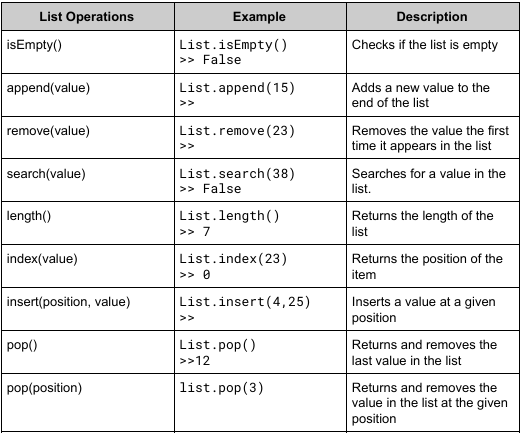
list operations

tuples

• an ordered set of values of any type is called a tuple

• a tuple is immutable, which means it cannot be changed: elements cannot be added or removed once it has been created

• tuples are initialised using regular brackets instead of square brackets

• tupleExample = (“Value1”, 2, “Value3”)

• elements in a tuple are accessed in a similar way to elements in an array, with the exception that values in a tuple cannot be changed or removed

  • attempting to do so will result in a syntax error.

linked lists

• dynamic data structure used to hold an ordered sequence

• items do not have to be in contiguous data locations

• each item is called a node, and contains a data field and a link or pointer field

• start node contains the first node

• data field - contains the actual data associated with the list

• pointer field - contains the address of the next item in the list

• when traversing a linked list, the algorithm begins at the index given by the ‘Start’ pointer and outputs the values at each node until it finds that the pointer field is empty or null

• this signals that the end of the linked list has been reached

• applications of linked lists

  • image viewers to switch between previous and next images

  • music players to store tracks in a playlist

  • browsers back and forward pages

operations on linked lists

• values can easily be added or removed by editing pointers

• add - adds node

• delete - removes node

• next - moves to the next item in the list

• previous - moves to the previous item in a doubly linked list

• traverse - a linear search through the list

adding an item to a linked list

1. check there is free memory for a new node

2. create a new node and insert data into the node

3. if the linked list is empty

   1. new node becomes the first node, create start pointer to it

4. if new node should be placed before the first node

   1. new node becomes first node, change starter pointer to it

   2. new node points to second node

5. if the new node is to be places inside the linked list

   1. start at first node

   2. if data in the current node is less than the value of the new node

      1. follow pointer to next node

      2. repeat until correct position if found or end of the list

   3. the new node is set to point to where the previous node pointed

   4. previous node is et to point to the new node

6. update the free pointer so it points to the next available storage space

removing at item from a linked list

1. check if list is empty

2. if the first item is the item to delete, set the start pointer to the next node

3. if the item to delete is inside the linked list

   1. start at the first node

   2. if the current node is the item to delete

      1. the previous nodes pointer is set to the next node

   3. follow the pointer to the next node

   4. repeated until the item is found or the end of the list is reached

4. update free pointer

traversing a linked list

1. check is list is empty

2. start at the node the start pointer is pointing to

3. output the item

4. follow the pointer to the next node

5. repeated until the end of the list is reached

graphs

• set of vertices/nodes connected by edges/arcs

  • directed graph - edges can only be traversed in one direction

  • undirected graph - edges can be traversed in both directions,

  • weighted graph - each arc has a cost attached to it

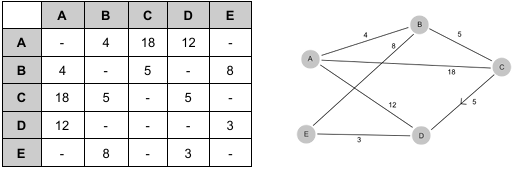
graphs - adjacency matrix

• convenient to work with

• easy to add nodes

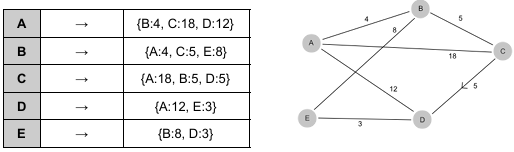
graphs - adjacency list

space efficient for large sparse networks

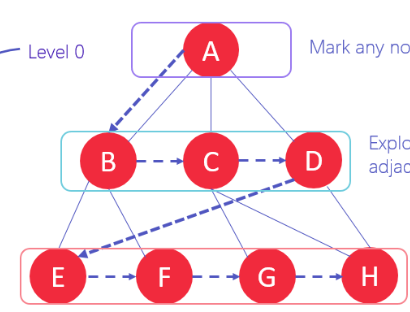
breadth first graph traversal

involves exploring all neighbouring nodes before moving to the next level of nodes, guaranteeing the shortest path in an unweighted graph, typically uses a queue data structure

1. set root node as current node

2. add current node to the list of visited nodes

3. for every edge connected to the vertex

   1. if the linked vertex is not in the visited list

      1. enqueue the linked vertex

      2. add the linked vertex to the visited list

4. dequeue and set the verted removed as the current node

5. repeated from step 2

6. output visited vertices

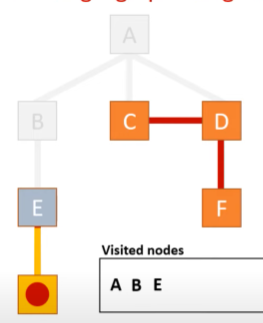
depth first graph traversal

method for traversing a graph that explores as far as possible along each branch before backtracking, typically uses a stack to remember the next vertex to visit

1. set the root node as the current node

2. add the current node to the list of visited nodes if it isn’t already on the list

3. for every edge connected to the node

   1. if the node is not in the visited list, push the linked node onto the stack

4. pop the stack and set the removed item as the current node

5. repeat step 2 until there are no nodes to visit

6. output all the visited nodes

stacks

• first in last out (FILO) data structure

  • items can only be added to/ removed from the top of the stack

• can be implemented as a static or dynamic structure

• stacks are implemented using a pointer which points to the top of the stack, where the next piece of data will be inserted

stack operations

• isEmpty - checks if the stack is empty

• push - adds value to the top / end of the stack

• peek - returns the top value from the stack without removing it

• pop - removes and returns the top value of the stack

• size - returns the size of the stack

• isFull - checks if the stack is full and returns the boolean value

queues

• first in first out (FIFO) data structure

• items are added to the end of the queue and are removed from the front of the queue

• queues are commonly used in printers, keyboards and simulators

• a linear queue is a data structure consisting of an array

• items are added into the next available space in the queue, starting from the front

• items are removed from the front of the queue

• queues make use of two pointers: one pointing to the front of the queue and one pointing to the back of the queue, where the next item can be added

queue operations

• enqueue - adds item to queue

• dequeue - removes item from queue

circular queue

• as the queue removes items, there are addresses in the array which cannot be used again, making a linear queue an ineffective implementation of a queue

• circular queues try to solve this

• a circular queue operates in a similar way to a linear queue in that it is a FIFO structure

• however, it is coded in a way that once the queue’s rear pointer is equal to the maximum size of the queue, it can loop back to the front of the array and store values here, provided that it is empty

• therefore, circular queues can use space in an array more effectively, although they are harder to implement

adding an item to a stack (push)

1. check for stack overflow - output error if stack is full

2. increment stack pointer so it points to the next available space

3. insert new data item at the location pointed to by the stack pointer

adding an item to a queue (enqueue)

1. check for queue overflow - output error if stack is full

2. increment the tail pointer

3. insert new data item at the location pointed to by the tail pointer

removing an item from a stack (pop)

1. check for stack underflow - if so output error

2. output the item pointed to by the pointer

3. decrement the pointer

removing an item from a queue (dequeue)

1. check for queue underflow - if so output error

2. output the data item pointed t by the head pointer

3. increment the head pointer

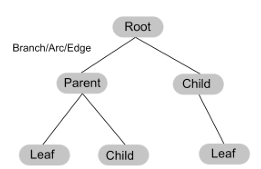
tree

• a tree is a connected form of a graph

• node - an item in a tree

• root - top node, no incoming nodes

• child - a node with incoming branches

• branch - connects two nodes together

• parent - a note with outgoing branches

• leaf - a node with no children

• subtree - subsection of a tree consisting of a parent and all the children of the parent

binary tree

• type of tree in which each node has a maximum of two children

• these are used to represent information for binary searches, as information in these trees is easy to search through

• the most common way to represent a binary tree is storing each node with a left pointer and a right pointer

• this information is usually implemented using two-dimensional arrays

pre-order tree traversal

• root node, left subtree, then right subtree

• Using the outline method, nodes are traversed in the order in which you pass them on the left, beginning at the left-hand side of the root node

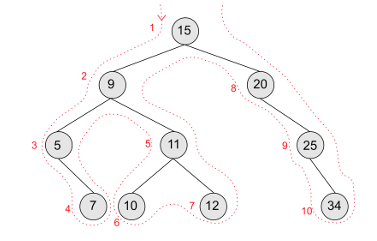
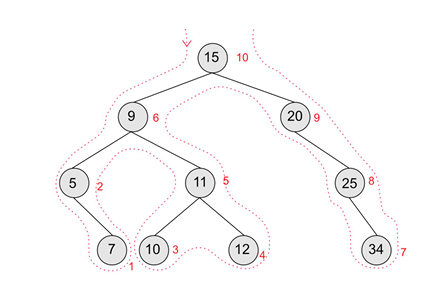
in-order tree traversal

• visit the left child, then the root node, and finally the right child.

• start on the very left point

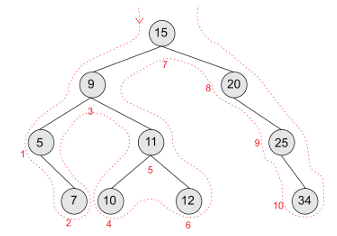
post-order tree Traversal

• left subtree, right subtree, root node

hash tables

• an array which is coupled with a hash function

• hash function takes in data (a key) and releases an output (the hash)

• the role of the hash function is to map the key to an index in the hash table

• each piece of data is mapped to a unique value using the hash function

• however, it is sometimes possible for two inputs to result in the same hashed value

• this is known as a collision

• a good hashing algorithm should have a low probability of collisions occurring but in the event that it does occur, the item is typically placed in the next available location

  • this is called collision resolution

• hash tables are normally used for indexing, as they provide fast access to data due to keys having a unique, one-to-one relationship with the address at which they are stored

reducing risk of collisions in hash

• increase the size of the hash table

• choose a good hash function

  • should distribute values uniformly across the hash table

  • avoid clustering — different inputs should produce different hashes