Calc test














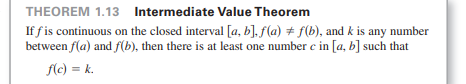




Got it! I'll combine the explanations and examples with the earlier notes, keeping everything organized. This way, the concepts flow together logically, with examples integrated where appropriate. I'll break it down so you can see how different situations fit within the broader context of limits and continuity.
1. Finding Limits Graphically and Numerically (Section 1.3)
Graphical Approach to Finding Limits
Graphically, you can estimate the limit of a function at a certain point by looking at the behavior of the function as xx approaches that point from both the left and right sides.
Key Observation: If the left-hand limit and the right-hand limit match at the point, and the function is defined there, then the limit exists and is equal to the function value.
Numerical Approach to Finding Limits
Numerically, you can approximate the limit by substituting values of xx that are increasingly close to the point of interest.
Key Ideas to Check for:
If the limits from the left and right are equal at a point, the limit exists.
If the function behaves differently on the left and right, the limit does not exist.
2. Evaluating Limits Analytically (Section 1.4)
When you evaluate limits analytically, we follow specific techniques to compute the limit at a point. Here's how we approach different situations:
1. Limit Exists and is Finite
If you’re evaluating limits where the function is continuous, you can directly substitute the value into the function.
Example: limx→2(x2)=22=4\lim_{x \to 2} (x^2) = 2^2 = 4
2. Limit Does Not Exist or Has a Discontinuity
If the limit from the left and right are different, the limit does not exist at the point.
Example: f(x)={x2,if x<23,if x=2x+1,if x>2f(x) = \begin{cases} x^2, & \text{if } x < 2 \\ 3, & \text{if } x = 2 \\ x + 1, & \text{if } x > 2 \end{cases}
Left-hand limit at x=2x = 2:
limx→2−f(x)=22=4\lim_{x \to 2^-} f(x) = 2^2 = 4Right-hand limit at x=2x = 2:
limx→2+f(x)=2+1=3\lim_{x \to 2^+} f(x) = 2 + 1 = 3Since the left and right limits are different, the limit does not exist at x=2x = 2.
3. Removable Discontinuity (If Limit Exists, but Function Value Doesn't Match Limit)
A removable discontinuity occurs when the function is undefined at a point, but the limit exists.
Example: f(x)=x2−1x−1f(x) = \frac{x^2 - 1}{x - 1}
Factor and simplify: f(x)=(x−1)(x+1)x−1=x+1for x≠1f(x) = \frac{(x - 1)(x + 1)}{x - 1} = x + 1 \quad \text{for } x \neq 1
As x→1x \to 1, the limit of f(x)=x+1f(x) = x + 1 is: limx→1f(x)=1+1=2\lim_{x \to 1} f(x) = 1 + 1 = 2
But the function is undefined at x=1x = 1, so it has a removable discontinuity at x=1x = 1.
4. Infinite Discontinuity (Vertical Asymptote)
An infinite discontinuity occurs when the function approaches ∞\infty or −∞-\infty as xx approaches a certain value.
Example: f(x)=1xf(x) = \frac{1}{x}
As x→0+x \to 0^+, f(x)→+∞f(x) \to +\infty.
As x→0−x \to 0^-, f(x)→−∞f(x) \to -\infty.
There is a vertical asymptote at x=0x = 0, and the limit does not exist.
3. Continuity and One-Sided Limits (Section 1.5)
Continuity at a Point
A function f(x)f(x) is continuous at x=cx = c if:
f(c)f(c) is defined.
limx→cf(x)\lim_{x \to c} f(x) exists.
limx→cf(x)=f(c)\lim_{x \to c} f(x) = f(c).
One-Sided Limits
One-sided limits refer to the behavior of a function as xx approaches a point from one direction only (either from the left or from the right).
Left-hand limit: limx→c−f(x)\lim_{x \to c^-} f(x)
Right-hand limit: limx→c+f(x)\lim_{x \to c^+} f(x)
Continuity and Discontinuities:
Jump Discontinuity: Occurs when the left-hand limit and right-hand limit at a point are not equal, and the function has a sudden jump at that point.
Example: f(x)={x+1,if x<23,if x=2x−1,if x>2f(x) = \begin{cases} x + 1, & \text{if } x < 2 \\ 3, & \text{if } x = 2 \\ x - 1, & \text{if } x > 2 \end{cases}
The left-hand limit at x=2x = 2 is 3, and the right-hand limit is 1, so the function is not continuous at x=2x = 2.
Removable Discontinuity: The function is undefined at a point, but the limit from both sides exists and is equal.
Example: f(x)=x2−1x−1f(x) = \frac{x^2 - 1}{x - 1}
The limit as x→1x \to 1 is 2, but the function is undefined at x=1x = 1, so it has a removable discontinuity.
4. Infinite Limits (Section 1.5)
Definition of Infinite Limits
Infinite limits occur when a function approaches +∞+\infty or −∞-\infty as xx approaches a certain point.
Example of Infinite Limits:
Vertical Asymptote:
Example: f(x)=1xf(x) = \frac{1}{x}
As x→0+x \to 0^+, f(x)→+∞f(x) \to +\infty.
As x→0−x \to 0^-, f(x)→−∞f(x) \to -\infty.
There is a vertical asymptote at x=0x = 0, meaning the limit does not exist in a finite sense.
Key Patterns to Look for:
1. Discontinuities:
Jump Discontinuity: Left-hand and right-hand limits are not equal.
Removable Discontinuity: Left-hand and right-hand limits exist and are equal, but the function is undefined or not equal to the limit at the point.
Infinite Discontinuity (Vertical Asymptote): As the function approaches a point, it goes to +∞+\infty or −∞-\infty.
2. Limits Not Existing:
Left-hand and right-hand limits are different.
Example: A function with a jump discontinuity.
Oscillatory behavior: The function does not settle to a single value (e.g., sin(1x)\sin\left(\frac{1}{x}\right)).
Recap of the Types of Limits/Discontinuities:
Continuous: Limit from the left and right are equal and match the function’s value.
Jump Discontinuity: Left-hand and right-hand limits are not equal.
Removable Discontinuity: Limit exists but the function is undefined or not equal to the limit.
Infinite Discontinuity: The function approaches ∞\infty or −∞-\infty as xx approaches a point.
Limit Does Not Exist: Either the left-hand and right-hand limits are different, or the function oscillates and does not approach a single value.
I hope this makes the information clearer and more organized for you! This combined approach should help you understand what to look for when dealing with limits and continuity in various situations. Let me know if you'd like to dive deeper into any part or need more examples!