2.3 Data Representation and Data Types (Binary, Hex, and Denary)

Bit

A bit is the smallest unit of data in computing. It is a binary digit that can hold either the value of 0 or 1.

Byte

A byte is a group of binary digits operated on as a unit. In most computer systems, a byte is made up of 8 bits.

Word

A word is the total number of bits that can be manipulated as a single unit by the CPU.

What is binary?

Base 2 system 0/1 whihc is computers language show with a 2 subscript₂

What is hexadecimal

Base 16 with going from 1-F (1-9 Then A-F representing 1-15) shown as₁₆

To convert divide by 16 to get the second digit and the remainder is the first

What is denary?

Base 10 decimal system with numbers₁₀ 1-9

Boolean

A Boolean data type represents truth values and can only take on two possible values: true or false.
May be stored in a single Bit as 1 if true and 0 if false.

Character

A character data type is used to store a single character, such as a letter, digit, or symbol. Characters are often represented using character encoding standards like ASCII or Unicode.
ASCII Character: 1 byte (8 bits). ASCII characters range from 0 to 127.

String

A string is a sequence of characters used to represent text. Unlike single characters, strings can vary in length.
The storage requirement for a string depends on its length and the encoding used.
For example, a string of length nnn in ASCII would require nnn bytes.

Integer

An integer data type is used to store whole numbers (i.e., numbers without a fractional part). Integers can be signed (allowing negative values) or unsigned (positive values only).
The storage requirement is 8-bit (1 byte) Integer: Ranges from −128-128−128 to 127127127 (signed) or 000 to 255255255 (unsigned).

Real

A real (or floating-point) data type is used to represent numbers with fractional parts, allowing for the representation of decimal points.
The storage requirement is 32-bit(4 bytes)

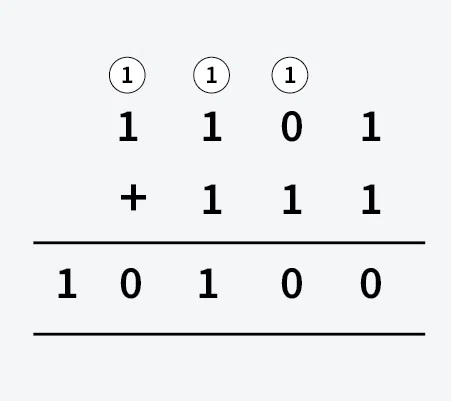
Binary addition

Use carrying for 2 ones just carry and put a zero. for/ one one place a 1

Start from least significant bit (left) and show overflow with a bracket

Underflow error

An underflow error occurs when a number is too small to be stored in the bits available. e.g., 0.00005 for a 3-bit value

Generally a number close to zero will round dound to zero as it cannot accutratly store teh data

Overflow error

An overflow error occurs when a binary value is too large to be stored in the bits available (not enough bits which can change signs and reduce precision). (e.g., 128 for an 8-bit value)

How to calculate absolute error

Absolute = original - new

The difference between the original number and the representation after truncation

How to calculate relative error

Relative = (absolute error /original num) * 100 %

What is sign and magnitude?

Makes use of the MSB to show the sign of a binary number.

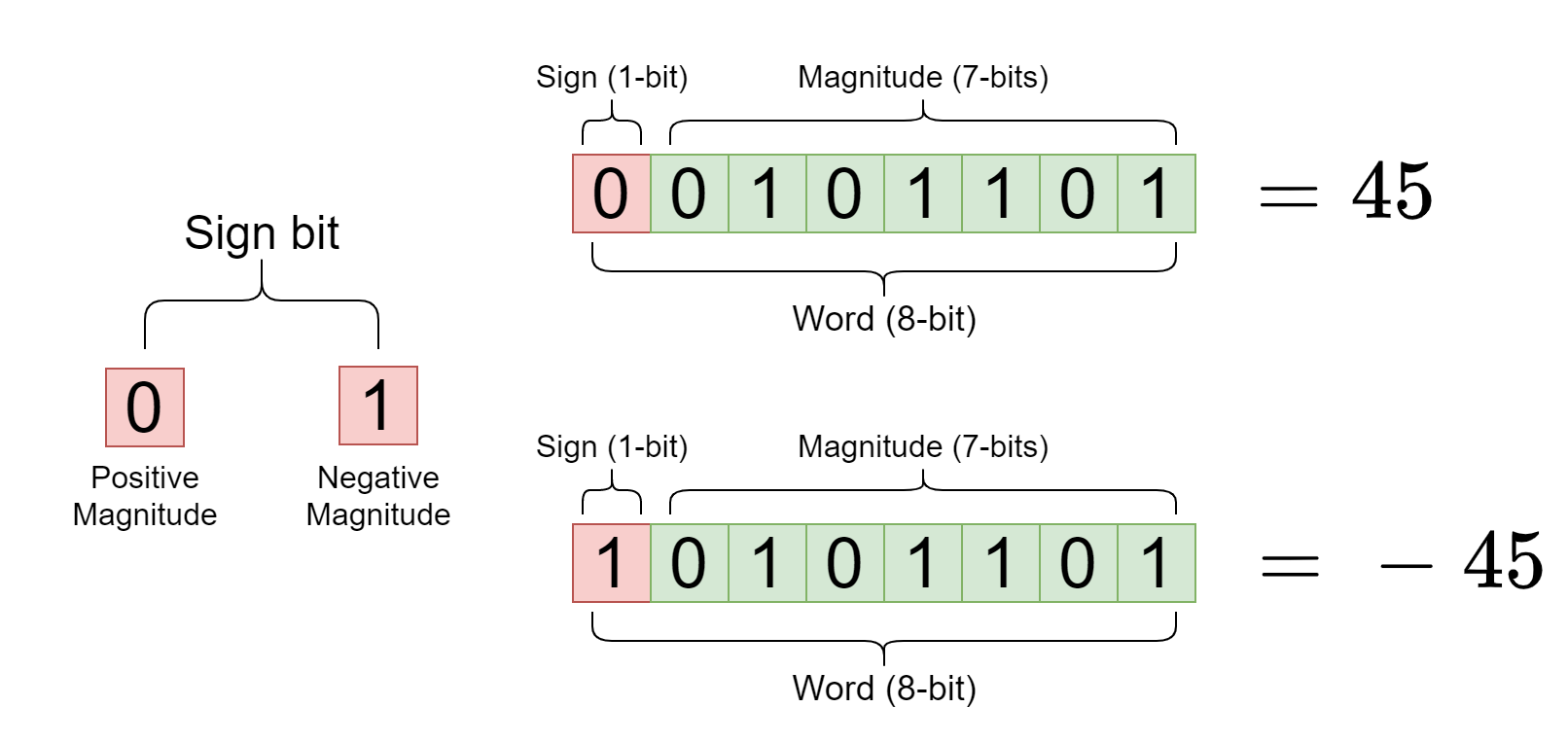
Why is sign and magnitude not used?

• Has to check the sign during binary arithmetic which creates overheads due to extra logic required (check sign, do calculation, update sign)

• You also lose MSB also so you cant store as high of a number

2's Complement

Method for representing signed (positive, negative, and zero) integers.
It works by starting with either -128 or 0 and adding on for every one that is there e.g.
-42 -> 11010110 (in two's complements)
-128+64+16+4+2 = -42

How to convert into 2’s complement

1. Start with binary positive absolute value

2. Invert all bits (1→ 0 then 0→1)

3. Add 1

The MSB acts as the starting point and shows the sign

How would we binary subtract?

You would invert the subtracted number into 2’s complement then add them and ignore any overflow that occurs

e.g.

16 - 12 = 10000 - 01100

16 + -12 = 10000 + 10100 = (1)00100 = 4 when overflwo ingnored

Binary Multiplication?

Use column multiplication (1×1 = 1 and timsing by zero equals 0)

Positive Whole Numbers (base 10) in Binary

The example in the picture represents 42 in 8-bit binary.

When representing a positive number in binary, it always starts from 0.

42 -> 00101010

This is wasteful, as zero can be represented twice

Negative Whole Numbers (base 10) in Binary (2 comp)

The example in the picture represents -42 in 8-bit binary.
When representing a negative number in binary, it always starts from 1.
-42 -> 11010110

What is a BCD?

Binary coded decimal (just binary and not twos complement) It will say if its twos complement.

Arithmetic and Logical Left-shift of binary

Left-shift means you are multiplying the binary by 2

In Arithmetic left-shift, if the binary starts with 1 that is, it's minus, you will keep the minus when you left shift.
Example: -42 -> 11010110 will be become 10101100
-128+32+8+4 = -84

In Logical left-shift, if the binary starts with 1, it will become 0, that is, the binary will become positive.
Example: -42 -> 11010110 will become 01010100
64+16+4 = 84

Arithmetic and Logical Right-shift of binary

Right-shift means you are dividing the binary by 2

In Arithmetic right-shift, if the binary starts with 1 that is, it's minus, you will keep the minus when you left shift.
Example: -42 -> 1101011 will be become 11101011
-128+64+32+8+2+1 = -21

In Logical right-shift, if the binary starts with 1, it will become 0, that is, the binary will become positive.
Example: -42 -> 11010110 will become 00010101
16+4+1 = 21

Whats a shift function?

Shifts all of the digits in a binary function to multiply or divide by powers of 2

Types of shift functions and what they each do

Logical shift - Shifts each binary digit with each vacted bit represented as a 0 (1011 → 1001 as the sign will stay the same)

Arithmetic shift - SImilar to logical but when performed to the right the sign bit retains its current value, which is good for negative numbers (1011 → 1101, which would be more accurate)

How do under/overflows affect shifts

1000 → 0000 would mean that you lose precision with the shift as we generally ignore overflows due to assigned bits

Logical vs Arithmetic shift?

Logical doesnt preserve vacant bits and Arithmetic shift moves bits and preserves the sign

Pros and cons of logical

+Simple multiplication and division

-Not suitable for signed numbers

Pros and cons of arithmetic?

+Preserves sign bit (good for signed nums and supports accuracy of calcs)

-Just a logical shift when going left

Real Numbers

Numbers with decimal places like 2.5 or 3.141592654

Standard Form

Large numbers represented as Mantissa x 10^exponent
0.65625 X 2^6 represent 42

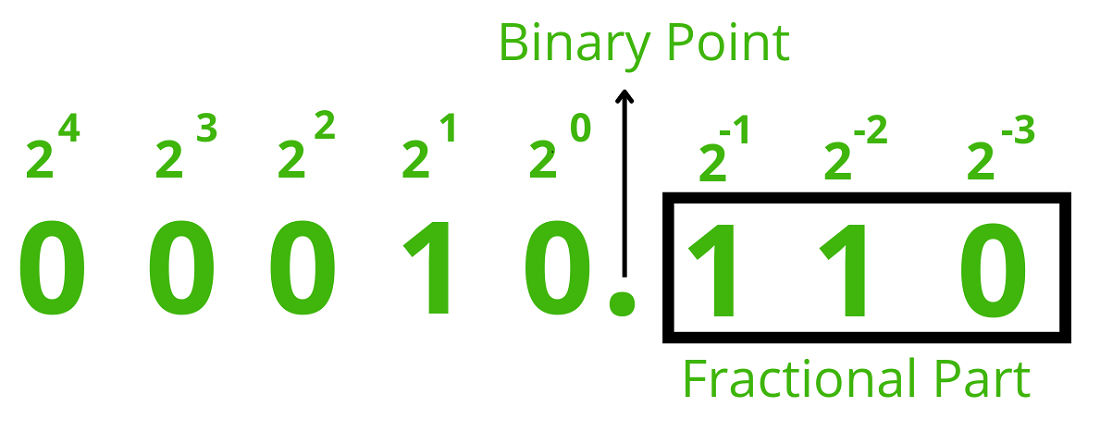
What is fixed point?

Where the decimal point is fixed (e.g. 4 bits before and 4 after)

What is Normalisation?

Converting a mantissa into a set for where the mantissa (where -1 =< mantissa < 1) in twos a complement so it is more precise. You would perform this be removing any leading (0s or 1s, 0 for normal and 1 for negative num) before the point and move the floating point.

What is normalisation used for?

Making a binary real shorter or more space efficient (gives better precision for adding to it)

Exponent and Mantissa

Mantissa x 10^exponent
Mantissa must be between -1 and 1
-1 <= Mantissa < 1

Exponent is part of a number indicating the power of the base

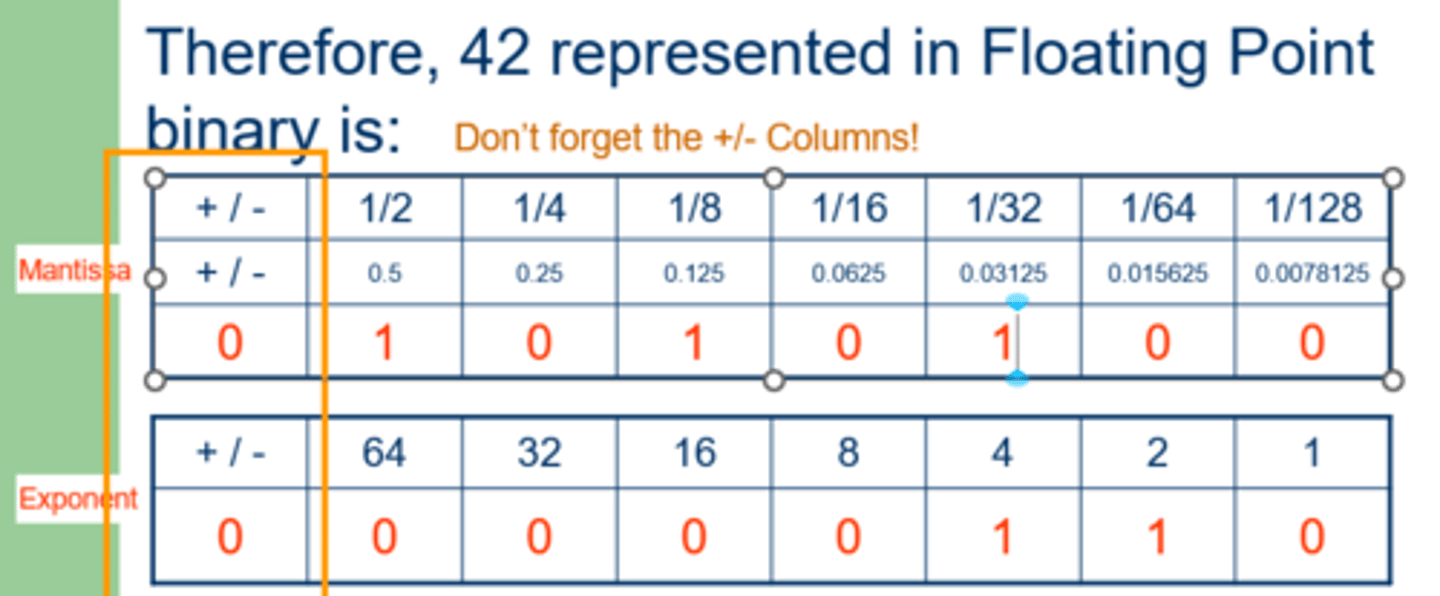
How to get exponent and mantissa

You will use a calculator to divide the number by 2 each time until you get an answer that's between 0.5 and 1. The answer is the mantissa. The number of 2 you use to get the answer is the exponent.

42 = 42 x 2^0 (no division)
42 = 21 x 2^2 (first division)
42 = 10.5 x 2^2 (second division)
42 = 5.25 x 2^3 (third division)
42 = 2.625 x 2^4 (fourth division)
42 = 1.3125 x 2^5 (fifth division)
42 = 0.65625 x 2^6 (sixth division)

The exponent is how many times the mantissa has been shifted during normalisation (as there will only be one number before the point)

What is range and precision?

Range - How large of a number representable

Precision - How precise a number you can represent

16-bit Floating Point

16-bit floating point uses 8-bits for the Mantissa and 8-bits for the Exponent.
Both parts could use Sign & Magnitude or Two's Complement representation.

Representing Mantissa in binary

The image show how to represent a Mantissa of 0.65625

Representing Exponent in binary

The image show how to represent an exponent of 6

16 bit floating point representation

Real Number to fixed point binary

The image shows 25.57 in fixed point binary.

Convert the 25 to binary, then convert .75 using 1/2, 1/4 and so on.

Difference between Floating Point and Fixed Point

Floating point
• It has set number of bits for mantissa and exponent
• trade-off between accuracy v range (as point moves)
• larger mantissa leads to greater accuracy
• larger exponent leading to greater range of numbers being represented
• It is not possible to represent zero.

Fixed point
• not flexible and has a set range and level of accuracy
• is less complex.

Floating point positives and negatives?

+Scalable - very large and small values can be represented+

+Precise and large range - for smaller numbers precision can be given and larger numbers can have the range

+Realistic - Can present a higher array of small numbers (good for calcs)

-Precise but still limited - by mantissa size

-Precision errors - rounding and truncation errors can occur as not all decimal fractions can be used

-Representation errors - Precision is not fixed so small representation errors may occur (like 0.1 not easily represented)

Hex to denary (base 10)

AD9C
(10 x 4096) + (13 x 256) + (9 x 16) + (12 x 1)
40960 + 3328 + 144 + 12 = 44444

Base 10 to Hex

50672
50672/4096 = 12 - C
12 x 4096 = 49152
50672 - 49152 = 1520
1520/256 = 5 - 5
5 x 256 = 1280
1520 -1280 = 240
240/16 = 15 - F
15 x 16 = 240
240 - 240 = 0 - 0
50672 -> C5F0

Binary to Hex

10101101111011

Split into group of four

0010 1011 0111 1011

2B7B

When splitting up the Binary into group of 4, always start at the RIGHT