Biostats Lect 1 & 2

Uses of Statistics

–Used to organize and summarize information

–Used to determine exactly what conclusions are justified based on the results that were obtained

•Population

–The set of all the individuals of interest in a particular study

–Vary in size; often quite large

Sample

–A set of individuals selected from a population

–Usually intended to represent the population in a research study

Variable

–Characteristic or condition that changes or has different values for different individuals

Datum (singular)

–A single measurement or observation

–Sometimes called a score or raw score

Data Set 

–A collection of measurements or observations from a sample or population

Relationship between a population and a sample in science.  

The population → sample from population → the sample (indiv. selected from pop) → results from sample are gener. to pop → population 

Parameter

–A value, usually a numerical value, that describes a population

–Derived from measurements of
the individuals in
the population

Statistic

–A value, usually a numerical value, that describes a sample

–Derived from measurements of
the individuals in
the sample

Average age of all freshmen at US universities

Parameter or Statistic 

Parameter 

Average age of all freshmen at USM

Parameter or Statistic

Statistic 

Descriptive Statistics

–Summarize data

–Organize data

–Simplify data

Inferential Statistics

–Study samples to make generalizations about the population

–Interpret experimental data

Independent Variable

•the variable manipulated by the researcher

–Independent because no other variable in the study influences its value

Dependent Variable

•the one observed to assess the effect of treatment

–Dependent because its value is thought to depend on the value of the independent variable

Goal of Experimental Method

–To demonstrate cause-and-effect relationship

Manipulation

–The levels of the independent variable are determined by the experimenter, and the effect on the dependent variable is measured.

Control

•rules out influence of other variables

–Participant variables (e.g. age, intelligence)

–Environmental variables (e.g. weather)

Variables 

–Cannot manipulate an independent variable, groups are determined by pre-existing values of quasi-independent variable (e.g. sex)

–A second variable is measured to see if there is a difference between groups

Discrete Variable 

–Has separate, indivisible categories

–No values can exist between two neighboring categories

Continuous Variable

–There are an infinite number of possible values between any two observed values.

–Is divisible into an infinite number of parts

Statistical notation “n”

the number of scores in a sample

Statistical Notation “N“

the number of scores in a population

Proportions

Measures the fraction of the total group that have same value, e.g. nursing majors

•Called relative frequencies because they describe the frequency (f) of some value in relation to the total number of scores (N)

Percentages

Expresses relative frequency out of 100

Proportion equation 

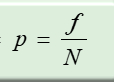
Percentages Equation

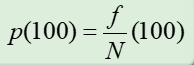
frequency distribution

an organized tabulation showing exactly how many individuals are located in each category on the scale of measurement.

•Can be structured either as a table or as a graph, and presents the same two elements:

–The set of categories that make up the original measurement scale

–A record of the frequency, or number of individuals in each category

Frequency distribution graph

•called a histogram, the score categories (x values) are listed on the x-axis and the frequencies of those x values are listed on the y-axis

•A vertical bar is centered above each score on the x-axis.  The height of the bar corresponds to the frequency of the corresponding x-axis.

Grouped Histograms

• When the number of categories is very large, they are combined, or grouped, in the table

• Information is lost when categories are grouped or combined

• Individual scores cannot be retrieved

• The wider the interval, the more information is lost

Smooth Curves on histogram

When populations are typically so large that individual scores are no longer large blocks, only pixels.

There are three characteristics that completely describe any distribution

Shape, central tendency, and variability

Central tendency

measures where the center of the distribution is located

Variability

measures the degree to which the scores are spread out over a wide range or are clustered together

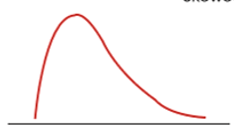
Positive or Negative 

Positive 

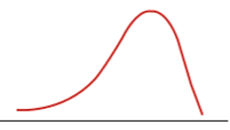
Positive or Negative 

Negative 

Percentile

for a particular x value is the percentage of individuals with scores equal to or less than that x value.