Lecture #12 & 13 | Models of Sequence Evolution

How to account for among site variation?

• Rate partitions for different genes or partitions thereof (eg. 1st, 2nd, and 3rd position of codons may have different rates)

• Gamma distribution rates (G)

• Allowance for a proportion of invariant sites (I)

• G + I

Gamma distribution of rates

Used to model site rate heterogeneity (quality or state of being diverse in character or content)

• Alpha is large: equal rate variation across all sites

• Alpha is small: rate variation across sites increases such that there are many sites with rates that approach 0 ad others with rates much higher

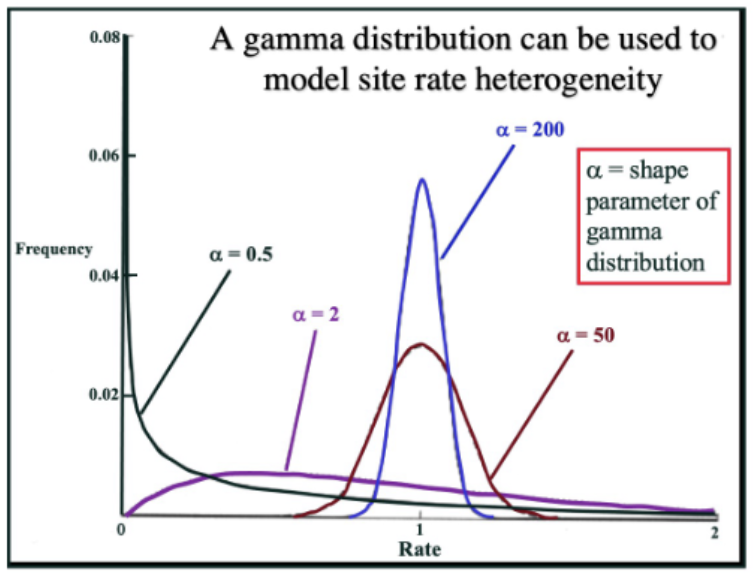
alpha=200 is more equal in variation than alpha = 2

Typical model= GTR + I + G

Maximum likelihood

A statistical model of tree creation that favors optimality

Goal: Find the tree that maximizes the probability of observing the data under a given model of sequence evolution

Requires:

1. A model of sequence evolution

2. A hypothesis (branching order and branch lengths)

3. The data (observed sequences)

Problems with Likelihood

Uses a fixed predetermined model, and produces a single tree

• Computationally difficult, especially for confidence intervals

• Model of evolution estimated and fixed prior to analysis

• Difficult to map characters

• Cannot treat gene regions separately in same analysis

ML tree is the tree with the highest likelihood

Bayesian Analysis

• An optimality criterion method

• Maximizes the posterior probability of observing the data under a given model of sequence evolution

• 

• Does not require initial model of sequence evolution

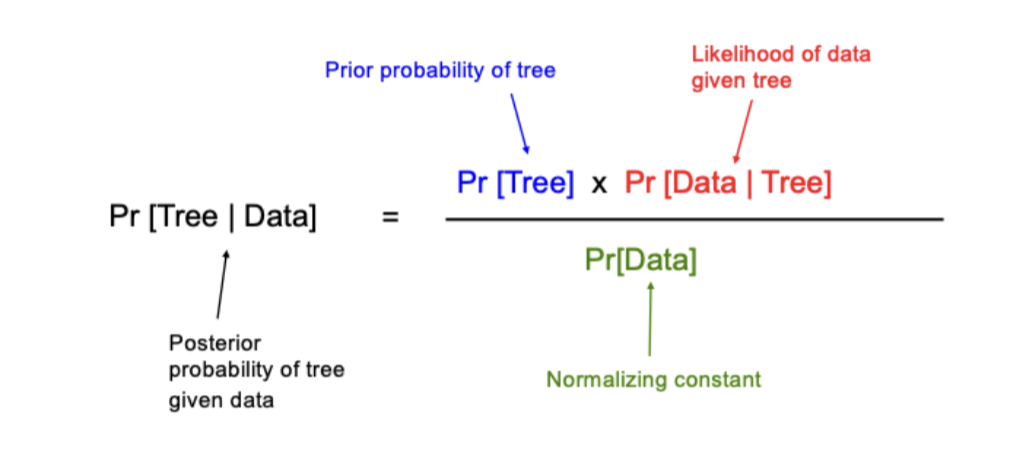
Problems with Bayesian interference

• To what extent is posterior distribution influenced by the prior

• How do we know that the chains have converged onto the stationary distribution

• Most common approach is to compare independent runs starting from different points in parameter space

• Tracking characters is a problem

Goal of bayesian analysis

Attain the best likelihood score (highest peak) possible, and to not get stuck on local peaks.

• all trees accepted are kept in memory and used to generate a 50% majority rule tree

  • produces a summary tree of all the most supported clades

• Will almost always be less resolved than a maximum likelihood result

Posterior Probabilities

Majority rules values

• used as a different measure of support from Bootstrap Support

• Generally much higher than Bootstrap values