P2

SCALARS

SCALARS

No direction

Speed distance mass

VECTORS

Have direction

Velocity displacement force

DISTANCE SPEED TIME

Distance = speed x time

ACCELERATION

Acceleration how quickly the velocity is changing

Acceleration FORMULA

Change in velocity (m/s) / time ( s )

Change in velocity = final velocity - initial velocity

UNIFORM ACCELERATION

(final velocity)* - (initial velocity)*= 2 x acceleration x distance

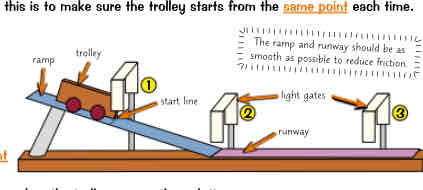
Acceleration practical

measure distance of light gate 12 23

Let it go down the ramp it will accelerate then reaching runway travels constant speed

Each light gate will record time

Gates 12 find avg speed on ramp

Gates 23 give speed on runway (distance/ti)

Acceleration increases as steepness of ramp

Or decreasing friction

Improve practical

Ruler for distance

Light here human error

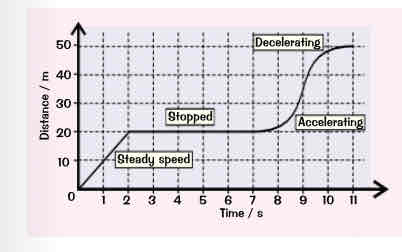
Distance time graph

The gradient (slope) at any point gives the speed of the object.
Flat sections are where it's stopped.
A steeper graph means it's going faster.
Curves represent acceleration.
A steepening curve means it's speeding up (increasing gradient).

A levelling off curve means it's slowing down (decreasing gradient).

Average speed

total distance / time taken

Speed of curved time

Find tangent

Then gradient

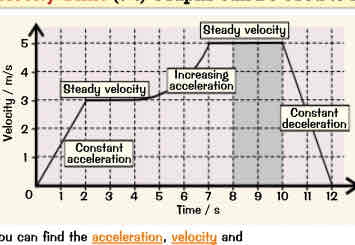
Velocity time graph

• Gradient = acceleration.
  Flat sections represent steady velocity.

• The steeper the graph, the greater the acceleration or deceleration.

• Uphill sections (/) are acceleration.
  Downhill sections (V are deceleration.

• 
  A curve means changing acceleration.

• 
  The area under any section of the graph (or all of it) is equal to the distance travelled in that time interval.

Forces

Contact touching

Non contact not touching

Interaction pair

Pair of equal and opposite forces acting on two different objects

Resultant force

Single force

Free body diagram

Diagram of object showing direction and size of the forces(vectors)

Zero resultant force

Stationary or moving at steady speed

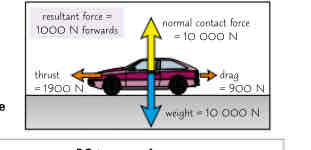
No zero resultant force

Object accelerate / deceleration

Thrust bigger than drag accelerate

Drag bigger than thrust deceleration

Normal contact force and weight balance out

Scale drawings

Find size and direction of resultant force

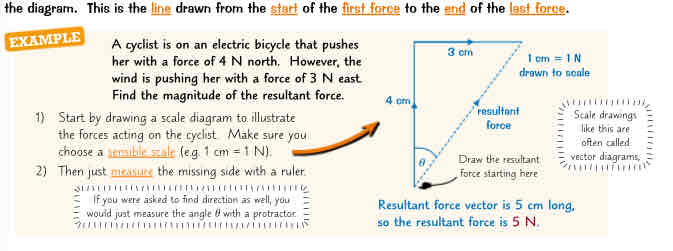
When is an object in Equilibrium

Zero resultant force

Resolve forces

Create right angle triangle at longest side

Measure the 2 lefts to find vertical and horizontal force

Newton’s first law

An object will remain stationary or at a constant velocity unless acted upon by an external force

Newton’s second law

Force acting on an object is equal to its rate of change of momentum

Resultant force = mass x acceleration

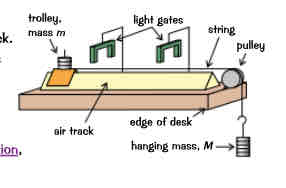
Experiment newtons second law

force acting on the trolley is equal to the weightof the hanging mass.

The hanging mass is released, pulling the trolley along the track.

By measuring the time and speed at which the trolley passes each light gate, its acceleration can be calculated.

You can increase the force acting on the trolley by moving one of the masses from the trolley to the hanging mass, and repeating the experiment.

If you plot your results on a graph of force against acceleration,you should get a straight line, showing that F= ma

Friction

Slows things down need an driving force

Driving force = to friction steady

Driving force >to friction acceleration

Driving force <to friction deceleration

Friction 2 surfaces

Terminal velocity

When objects first set off they have more driving force than friction force (resistance), so they accelera But the resistance is directly proportional to the velocity of the object — resistance or velocity. So as the velocity increases, the resistance increases as well. This gradually reduces the acceleration until the friction force is equal to the driving force so it doesn't accelerate any more. The forces are balanced (there's no resultant force). The object will have reached its maximum velocity or terminal velocity.

Terminal example

1. skydiver accelerates as weight due to gravity > air resistance.

2. But air resistance increases as velocity increases until weight = air resistance, and they reach terminal velocity.

3. The parachute opens and weight < air resistance, so they decelerate.

4. As velocity decreases, the air resistance also decreases until
   weight = air resistance - they reach a new terminal velocity

Terminal velocity 2

Grater drag lower terminal velocity

Drag depends on shape and area

Open parachute more area and air restrictions

Decreasing drag makes things faster

Inertia

How difficult to change an object velocity

Interim mass = f/a

Larger internal mass requires a larger force

Newton’s third law

2 objects interact the forces they exert on each other are equal and opposite

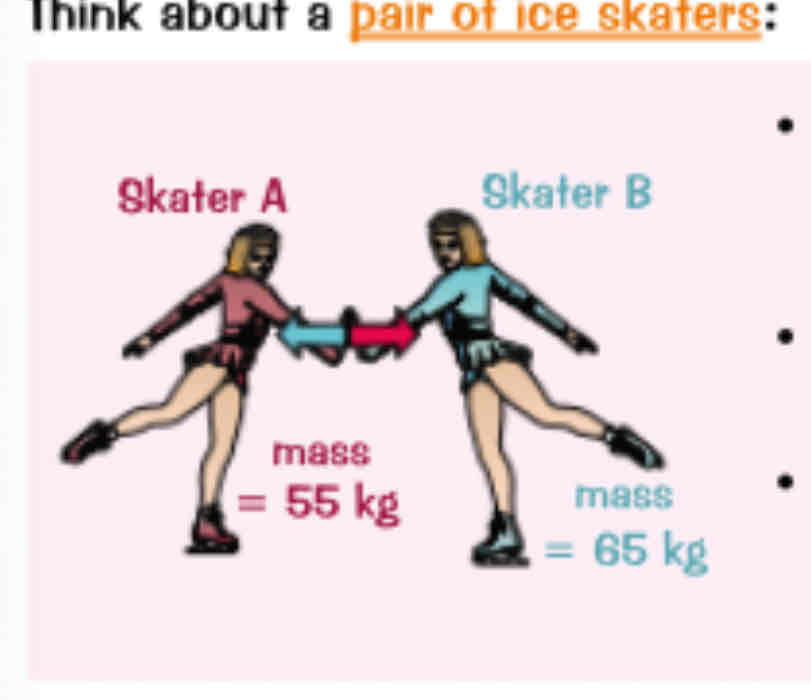
Where do they go

When skater A pushes on skater B (the 'action' force), she feels an equal and opposite force from skater B's hand (the

'reaction' force).

• Both skaters feel the same sized force, in opposite directions, and so accelerate away from each other.

Skater A will be accelerated more than skater B, though, because she has a smaller mass, so a smaller inertia -

a = F/m (from rearranging Newton's Second Law).

Object in equilibrium ain’t the same

The weight of the book pulls it down, and the normal reaction force from the table pushes it up.

This is NOT Newton's Third Law. These forces are different types and they're both acting on the book.

The pairs of forces due to Newton's Third Law in this case are:

The weight of book is pulled down by gravity from Earth (W.) and the book also pulls back up on the Earth (W.).

The normal contact force from the table pushing up on the book (R.) and the normal contact force from the book pushing down on the table (R).

Momentum

momentum (kg m/s) = mass (kg) x velocity (m/s)

examples of mom

faster momentum bigger the force

law of conservation of momentum

In a collision when no other external forces act, momentum is conserved

— i.e. the total momentum after the collision is the same as it was before it.

Momentum exa

If they join together it’s

Total momentum after = (Ma+Mb)xV

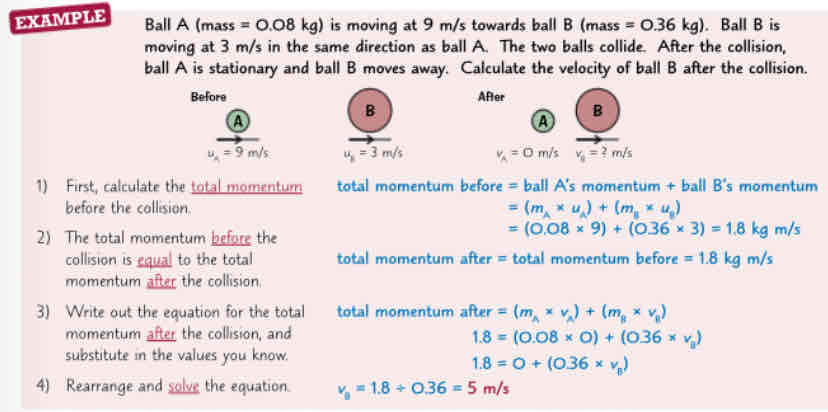
Elastic in elastic

Kinetic energy saved

Kinetic energy transfrred

Mass weight gravity

Everything has gravitational field

Gravity force is worthy

gravitational force (N)

= mass (kg) × gravitational field strength, g (N/kg)

Gravitational field makes all thing accelerate toward plant surface

Gravitational potential energy

gravitational potential energy(j)= mass(kg)Xgravitational field strength, g (N/kg)x height (m)

Kinetic energy store

kinetic energy = 0.5 x mass x(speed)2

Work done

When a FORCE makes an object MOVE, ENERGY IS TRANSFERRED and WORK IS DONE.

work done (J) = force (N) x distance (m)

Equal to energy transferred to kinetic energy if no friction

Power

Power is the rate at which energy is transferred

power (W) = work done (j) / time

Elastic and plastic

Stretch compressed or bend deformation

Returns to shape elastic

Doesn’t return to shape plastic

Hooked law

Extension of a spring (or any elastic object) is directly proportional to the force applied, as long as the limit of proportionality isn’t exceeded

f=kx

F force k spring constant x extension

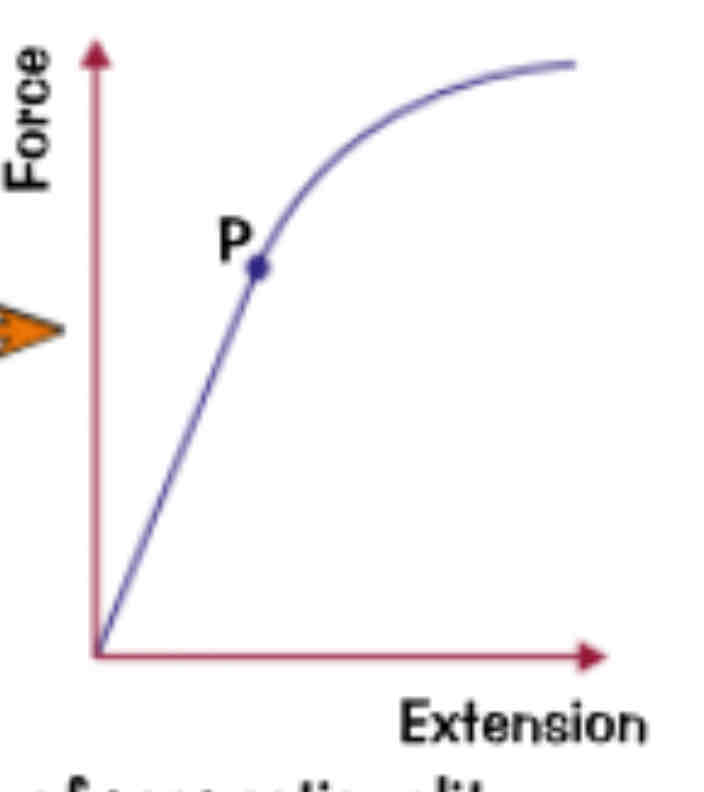
Limits of Hooke law

There’s a maximum limit to how much force can be applied before Hooke’s Law no longer applies.

• Beyond this limit (point P on the graph), the material behaves non-linearly and may undergo plastic deformation.

Fatter forces

Small forces result in linear (proportional) extension.

• Larger forces cause non-linear extension, and materials may not return to their original shape.

Spring experiment

• Attach a spring to a clamp stand and measure its original length.

• Add weights one by one to the spring, measuring its new length each time to calculate the extension (new length - original length).

• Plot a graph of force (weight) vs. extension and draw a line of best fit to observe if it follows Hooke’s Law (a straight line up to the elastic limit, then curves).

Work Done to Deform an Object:

• When a force stretches or compresses an object, it does work, transferring energy to the object’s elastic potential energy store.

• The formula for energy transferred in stretching (elastic potential energy) is

energy transferred in stretching = 0.5 x spring constant x (extension)?

Also doing area under graph

Moments

Turning effect on a force

Force on a pivot

Moment (Nm) = force (N) x distance

Larger force larger moment

Larger distance larger moment

Maximum moment push at right angles perpendicular to spanner

Levers as Force Multipliers

Levers help increase the force applied by reducing the input force needed to lift a load.

• The moment (turning effect) due to a force depends on the distance from the pivot.

• By increasing the distance from the pivot, less force is required to achieve the same moment.

• Common examples of levers include long bars, wheelbarrows, and scissors.

Gears

Gears are circular cogs with teeth that interlock to transfer rotation.

• When one gear turns, it causes the next gear to turn in the opposite direction.

• A small gear applies force to a larger gear, amplifying the moment but reducing the rotational speed.

Gear ratio

For example, if a large gear has twice as many teeth as a smaller gear, the smaller gear will turn twice for each turn of the large gear.

• The speed and moment transferred between gears depend on the ratio of their sizes.

Pressure

Pressure in a fluid is transmitted equally in all directions and it causes a force at right-angles to any surface.

Pressure force over area

Liquids are in compressible

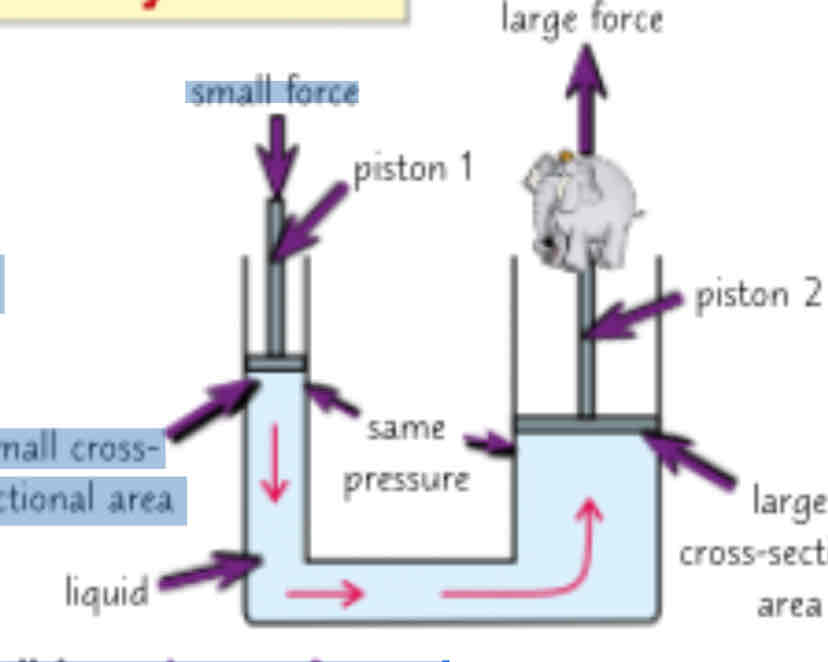
Hydraulic systems

Hydraulic systems are used as force multiplier they use a small force to produce a bigger force

The diagram to the right shows a simple hydraulic system.

The system has two pistons, one with a smaller cross-sectional area than the other.Pressure is transmitted equally through aliquid — so the pressure at both pistons is the same.

p = F ÷ A, so at the Ist piston, a pressure is

small cross-sectional area

exerted on the liquid using a small force over a small area.

This pressure is transmitted to the 2nd piston.

The 2nd piston has a larger area, and so as F = p X A, there will be a larger force.