Graph Identification and Derivative Rules

y=e^x

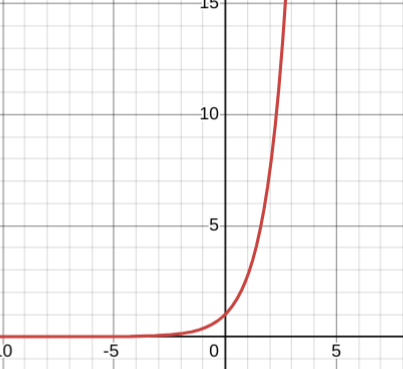
y=e^x+5

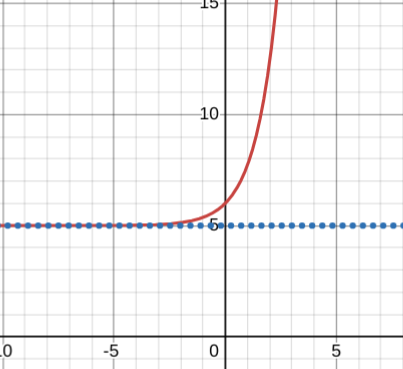
y=e^-x

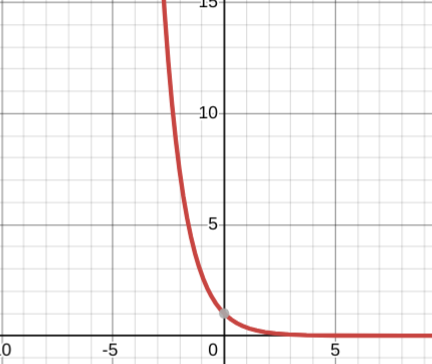
y=-e^x

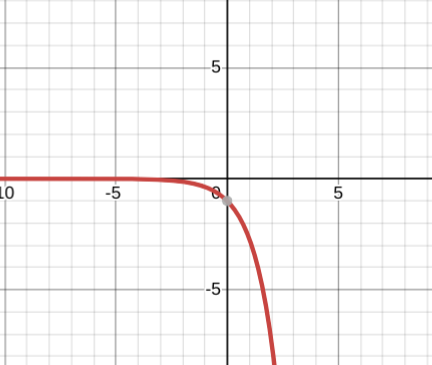
y=-e^-x

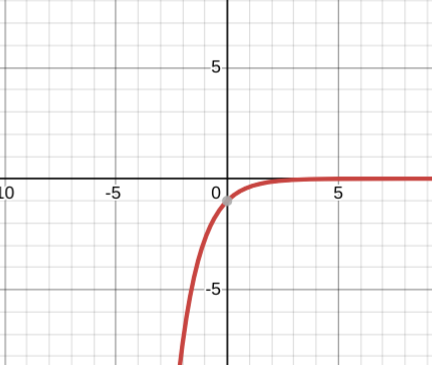
y=lnx

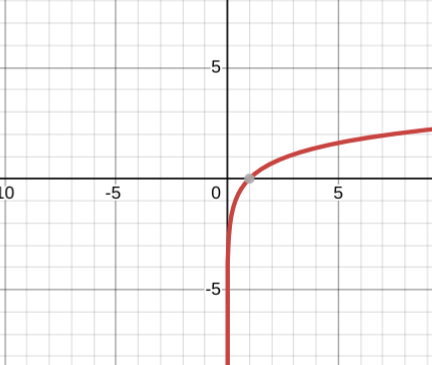
y=ln(x+5)

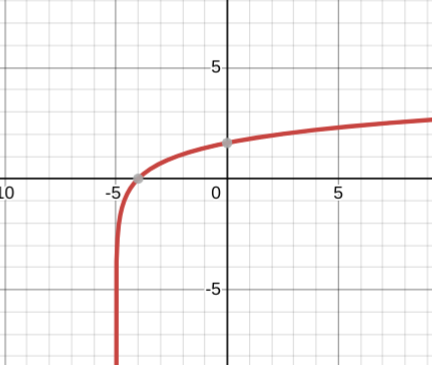
y=ln(-x)

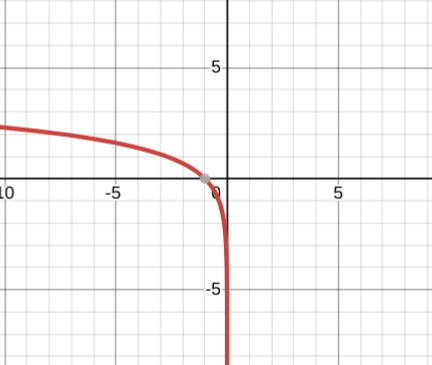
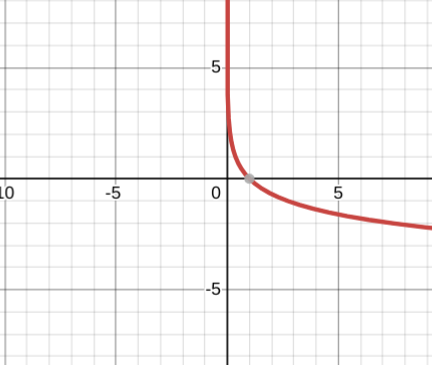
y=-lnx

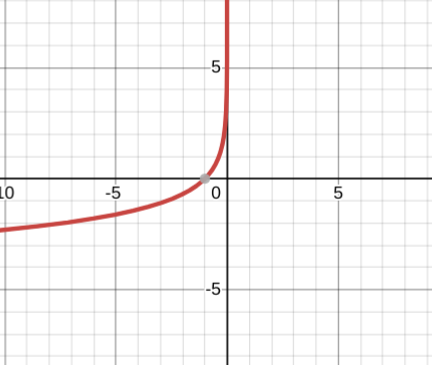
y=-ln(-x)

constant rule

derivative of a constant is zero.

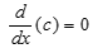
constant multiple rule

derivative of a constant multiplied by a fxn is the constant times the derivative of the fxn.

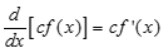
power rule

the derivative of x^n is n*x^(n-1), where n is a real number.

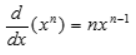
sum and difference rule

the derivative of a sum or difference of fxns is the sum or difference of their derivatives.

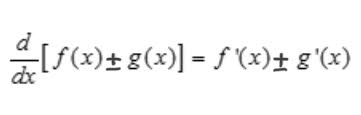
product rule

the derivative of a product of two fxns is the first fxn times the derivative of the second plus the second fxn times the derivative of the first.

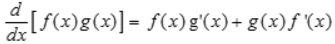
quotient rule

derivative of a quotient of two fxns is the denom x the derivative of the num - the num x the derivative of the denom, / denom²

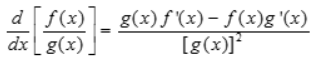
chain rule

differentiate the outer fxn while keeping the inner fxn the same. multiply this by the derivative of the inner function.

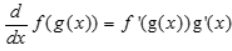
derivative of e^x

e^x itself

derivative of a^x

a^x ln(a)

derivative of e^g(x)

e^g(x) g'(x)

derivative of a^g(x)

ln(a) a^g(x) g’(x)

derivative of ln(x)

1/x, x>0

derivative of ln(g(x))

g'(x)/g(x)

derivative of log_a(x)

1/xln(a), x>0

derivative of log_ag(x)

g’(x)/g(x)ln(a)

derivative of sin x

cos x

derivative of cos x

-sin x

derivative of tan x

sec² x

derivative of csc x

-csc x cot x

derivative of sec x

sec x tan x

derivative of cot x

-csc² x

half angle of sin² x

1/2(1-cos(2x)) - sin s for sad, sad face :( minus

half angle of cos² x

1/2(1+cos(2x)) - cos c for congratulations, happy face :) plus

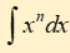
integral power rule

add one to the exponent and bring 1/n+1 to the front

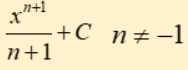
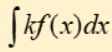
integral constant multiples rule

any constant in an integral is brought to the front

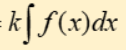
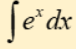
integral of exponential e

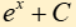
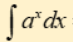
integral of exponential a

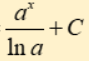
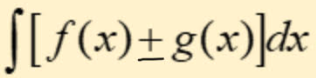
integral sums and differences

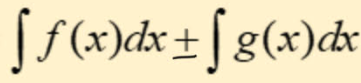
arcsin

Domain: [-1, 1]

Range: [-π/2, π/2]

arccos

Domain: [-1, 1]

Range: [0, π]

arctan

Domain: [-∞, ∞]

Range: [-π/2, π/2]

arccot x

D: (-∞,∞)

R: (0,π)

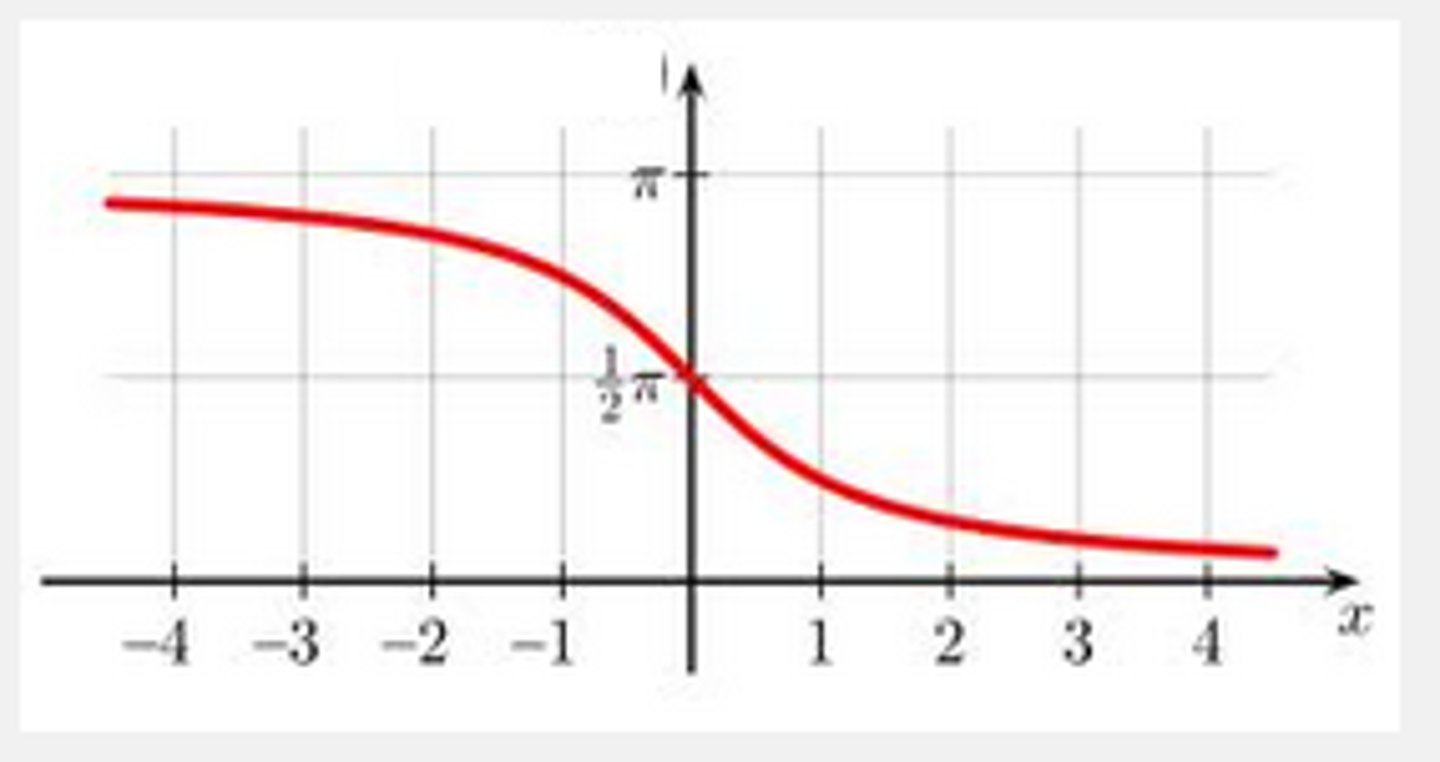
arcsec x

D: (⁻∞ , -1] U [1 , + ∞)

R: [0 , π/2) U (π/2 , π]

arccsc x

D: (⁻∞ , -1] U [1 , + ∞)

R: (-π/2, 0) U (0, π/2]

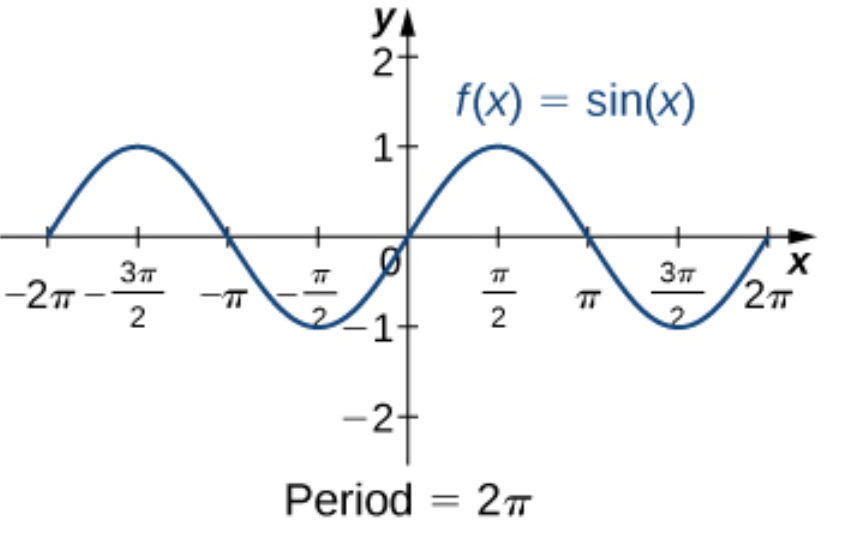
sin(x)

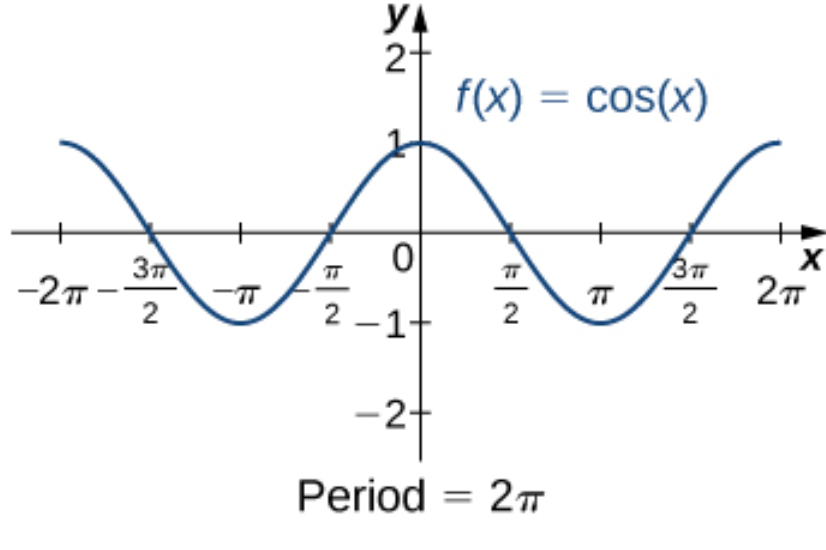
cos(x)

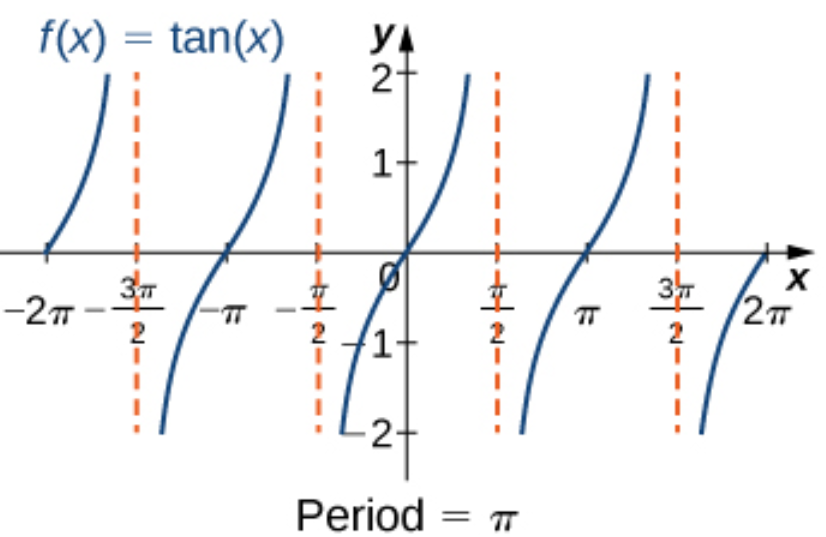
tan(x)

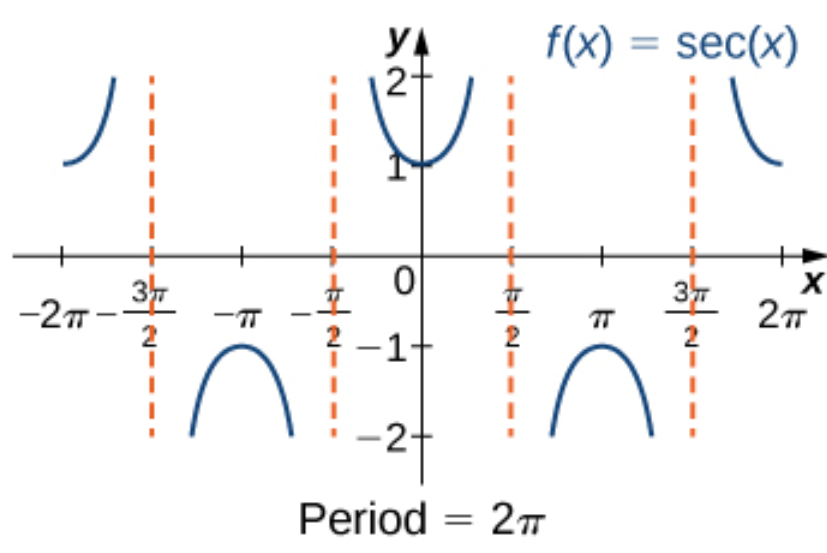
sec(x)

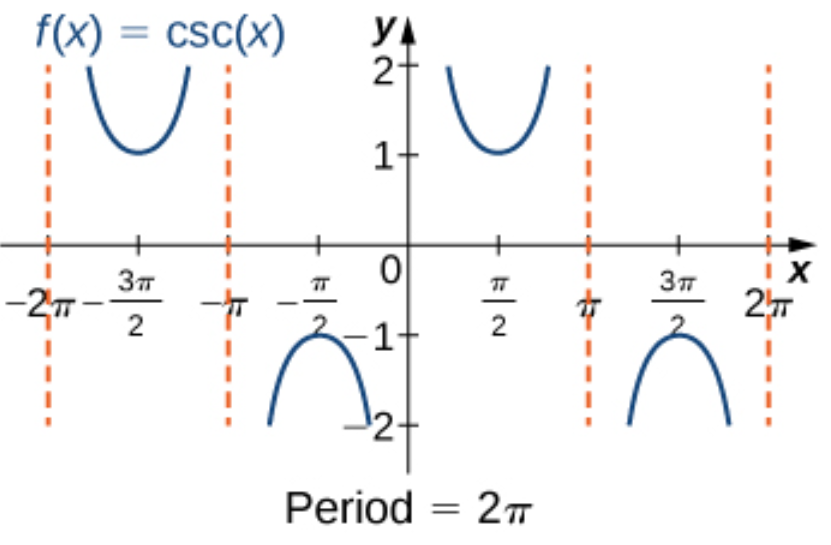
cosec(x)

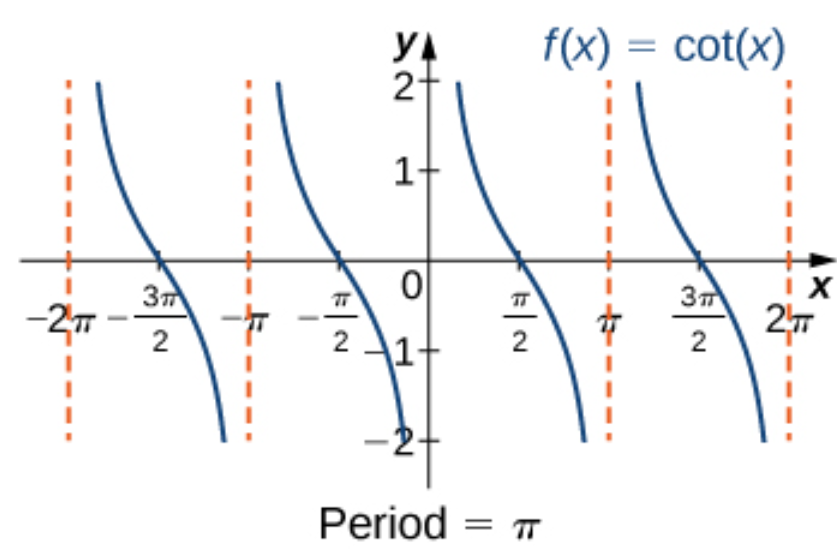
cot(x)

y = x⁻²

Domain: (-ꝏ,0) U (0,ꝏ)

Range: (0,ꝏ)

y = x²

Domain: (-ꝏ,ꝏ)

Range: [0,ꝏ)

y = x³

Domain: (-ꝏ,ꝏ)

Range: (-ꝏ,ꝏ)

y = x¹/²

Domain: [0, ꝏ)

Range: [0,ꝏ)

y = x¹/³

Domain: (-ꝏ,ꝏ)

Range: (-ꝏ,ꝏ)

y = x⁻¹ or 1/x

Domain: (-ꝏ,0) U (0,ꝏ)

Range: (-ꝏ,0) U (0,ꝏ)

y = sin(x)

Domain: (-ꝏ,ꝏ)

Range: [-1,1]

y = cos(x)

Domain: (-ꝏ,ꝏ)

Range: [-1,1]

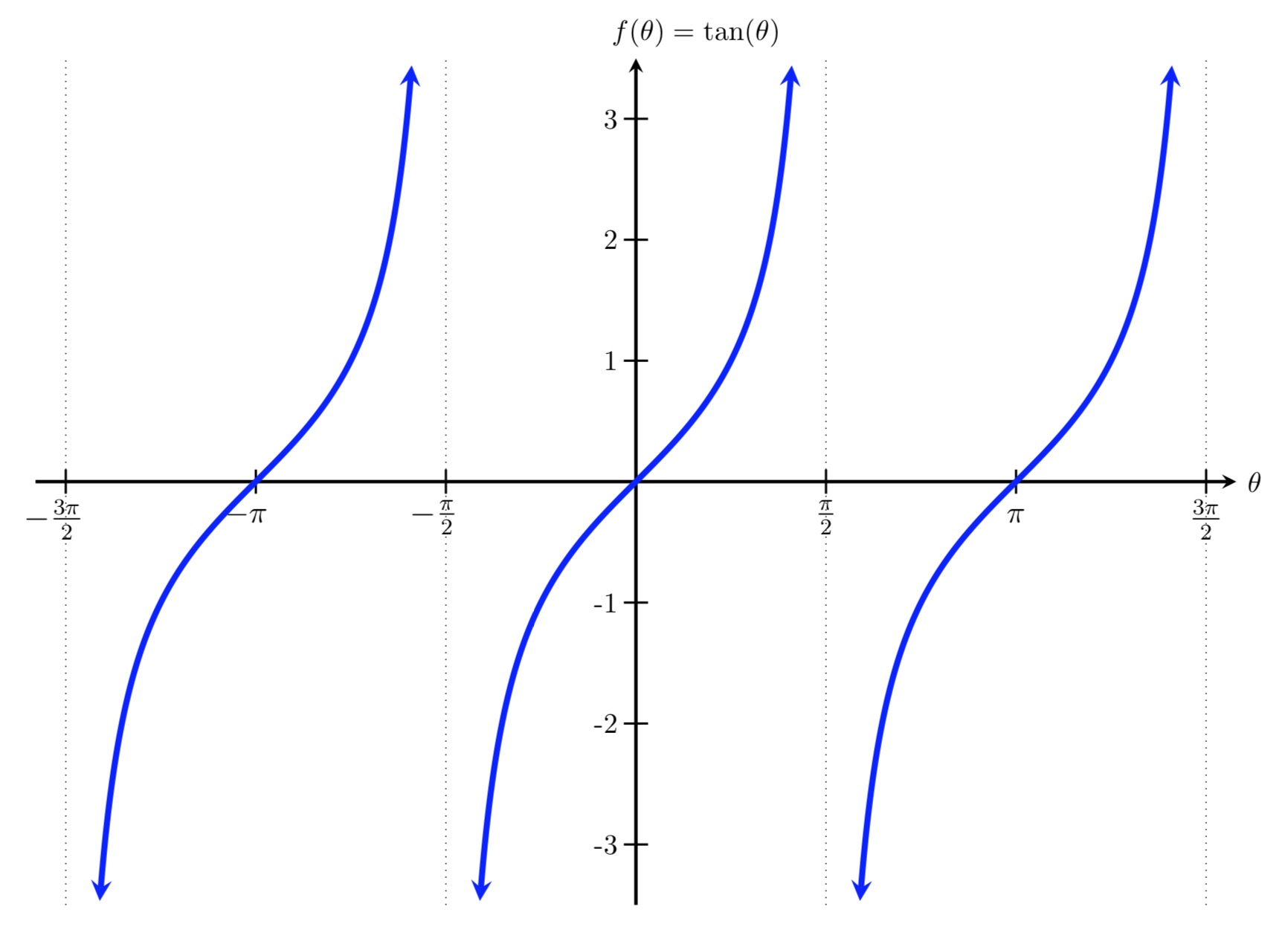
y = tan(x)

Domain: {x ≠ (2k+1)π/2}

Range: (-ꝏ,ꝏ)

y = cot(x)

Domain: {x ≠ kπ}

Range: (-ꝏ,ꝏ)

y = sec(x)

Domain: {x ≠ (2k+1)π/2}

Range: (-ꝏ,-1] U [1,ꝏ)

y = csc(x)

Domain: {x ≠ kπ}

Range: (-ꝏ,-1] U [1,ꝏ)

y = sin⁻¹(x)

Domain: [-1,1]

Range: [-π/2,π/2]

y = cos⁻¹(x)

Domain: [-1,1]

Range: [0,π]

y = tan⁻¹(x)

Domain: (-ꝏ,ꝏ)

Range: (-π/2,π/2)

y = cot⁻¹(x)

Domain: (-ꝏ,ꝏ)

Range: (0,π)

y = sec⁻¹(x)

Domain: (-ꝏ,-1] U [1,ꝏ)

Range: [0,π/2) U (π,3π/2)

y = csc⁻¹(x)

Domain: (-ꝏ,-1] U [1,ꝏ)

Range: (0,π/2) U (π,3π/2)

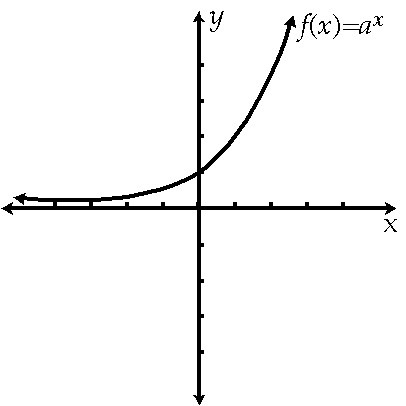
f(x) = bˣ, if b>1

Domain: (-ꝏ,ꝏ)

Range: (0,ꝏ)

f(x) = bˣ, if 0 < b < 1

Domain: (-ꝏ,ꝏ)

Range: (0,ꝏ)

f(x) = log_b(x), b > 1

Domain: (0,ꝏ)

Range: (0,ꝏ)

f(x) = logb(x), 0 < b < 1

Domain: (0,ꝏ)

Range: (0,ꝏ)

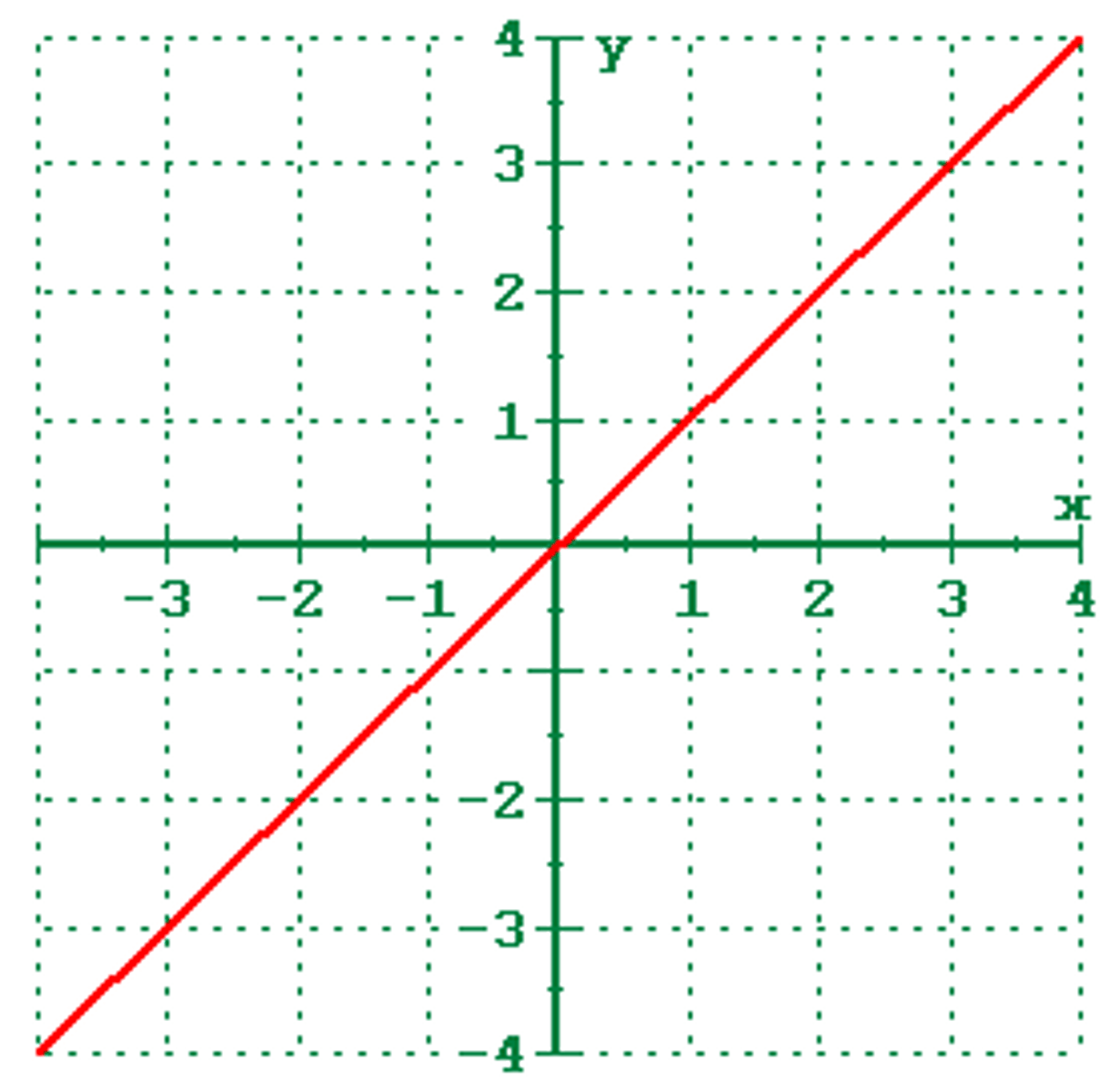
Linear function

f(x)= Mx + b

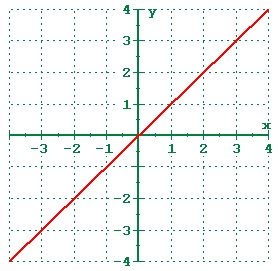
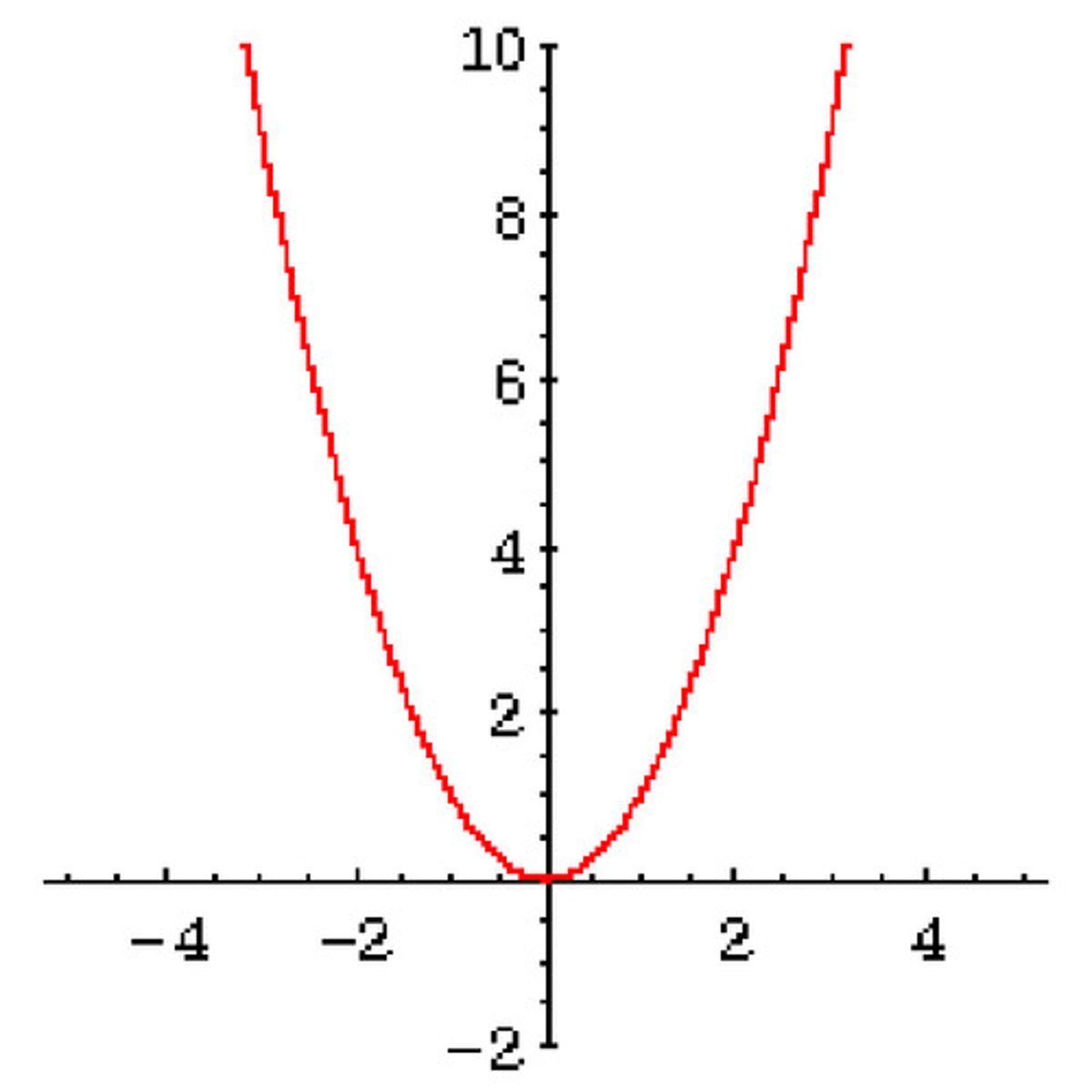
Quadratic / Square function

F(x) = x²

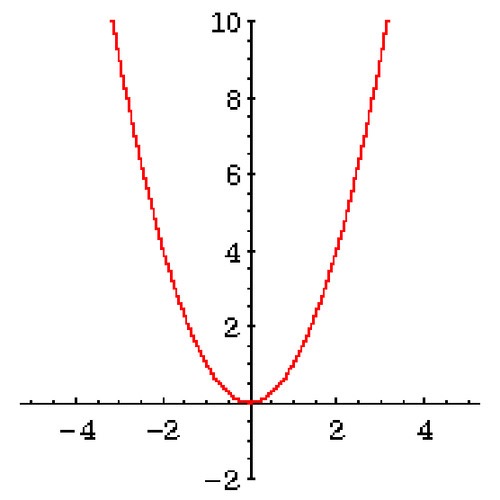
Cubic function

F(x)= x³

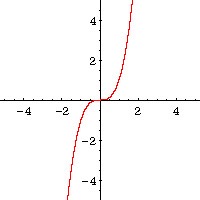
Square root function

F(x) = √x

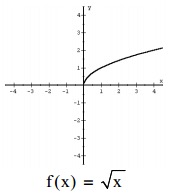
Cube root function

F(x) = 3√x

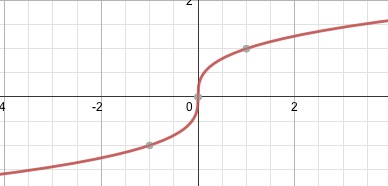
Reciprocal / Rational function (Odd)

F(x)= 1/x or f(x) = 1/x^n → n is an odd number

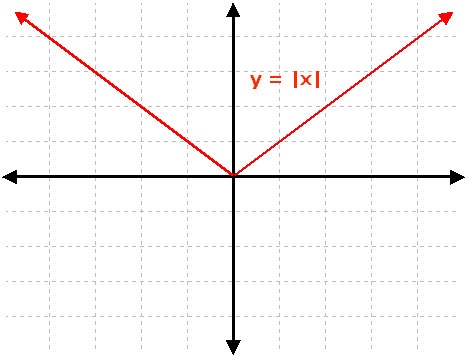
Absolute value function

F(x) = | x |

Exponential function

F(x) = e^x

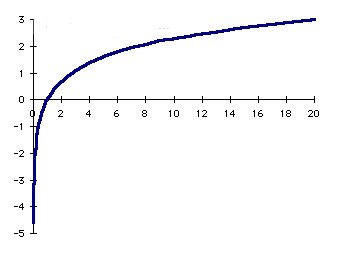
Natural logarithmic function

F(x) = ln(x)

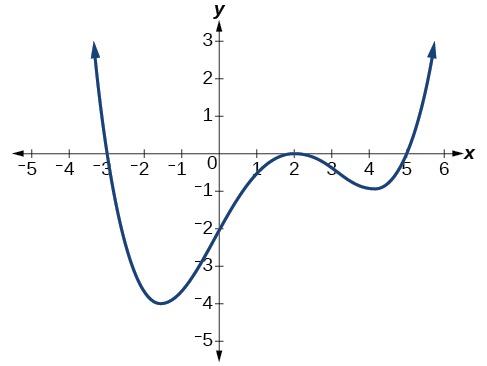
Polynomial function

Tangent function

F(x) = tan(x)

Cosine function

F(x) = cos(x)

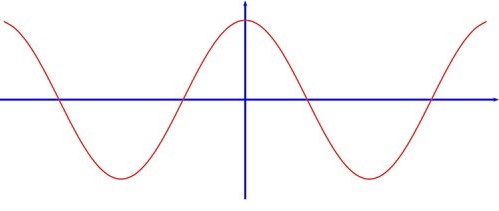
Sine function

F(x) = sin(x)

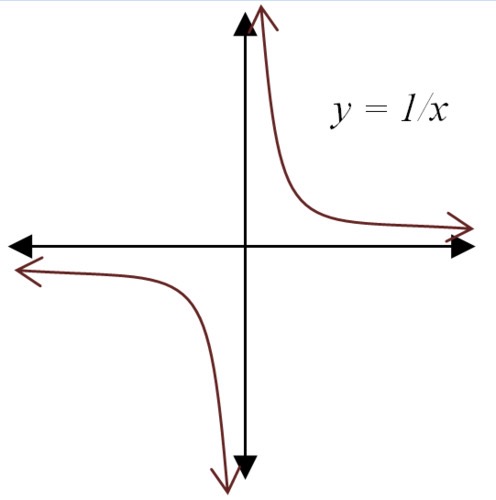
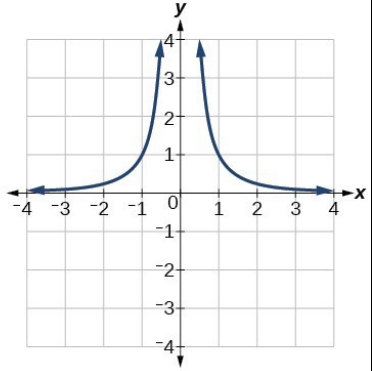
Reciprocal/ Rational function (Even)

F(x) = 1/x² or f(x) = 1/x^n → n is an even number

Identity

y = x

Squaring

y = x^2

Cubing

y = x^3

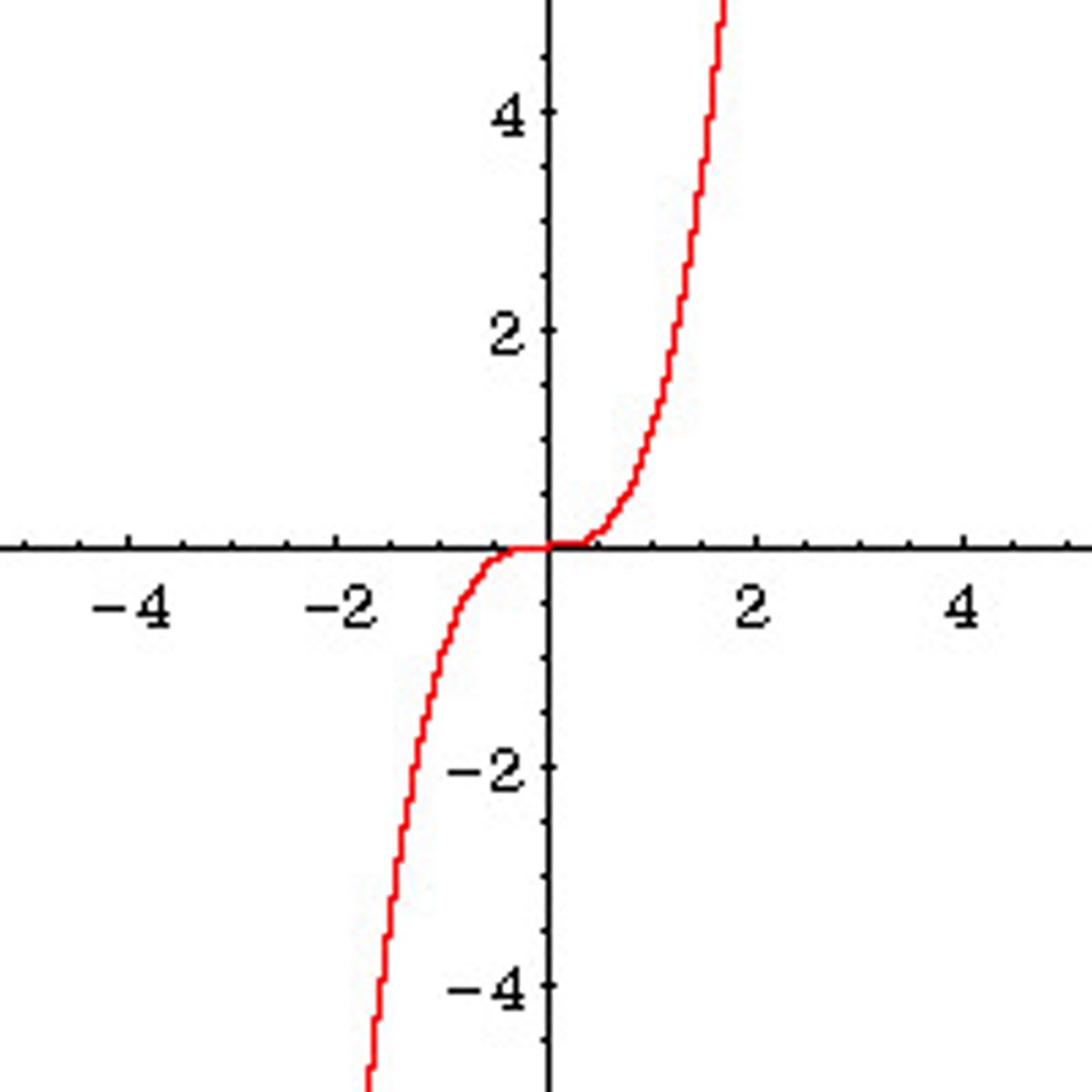
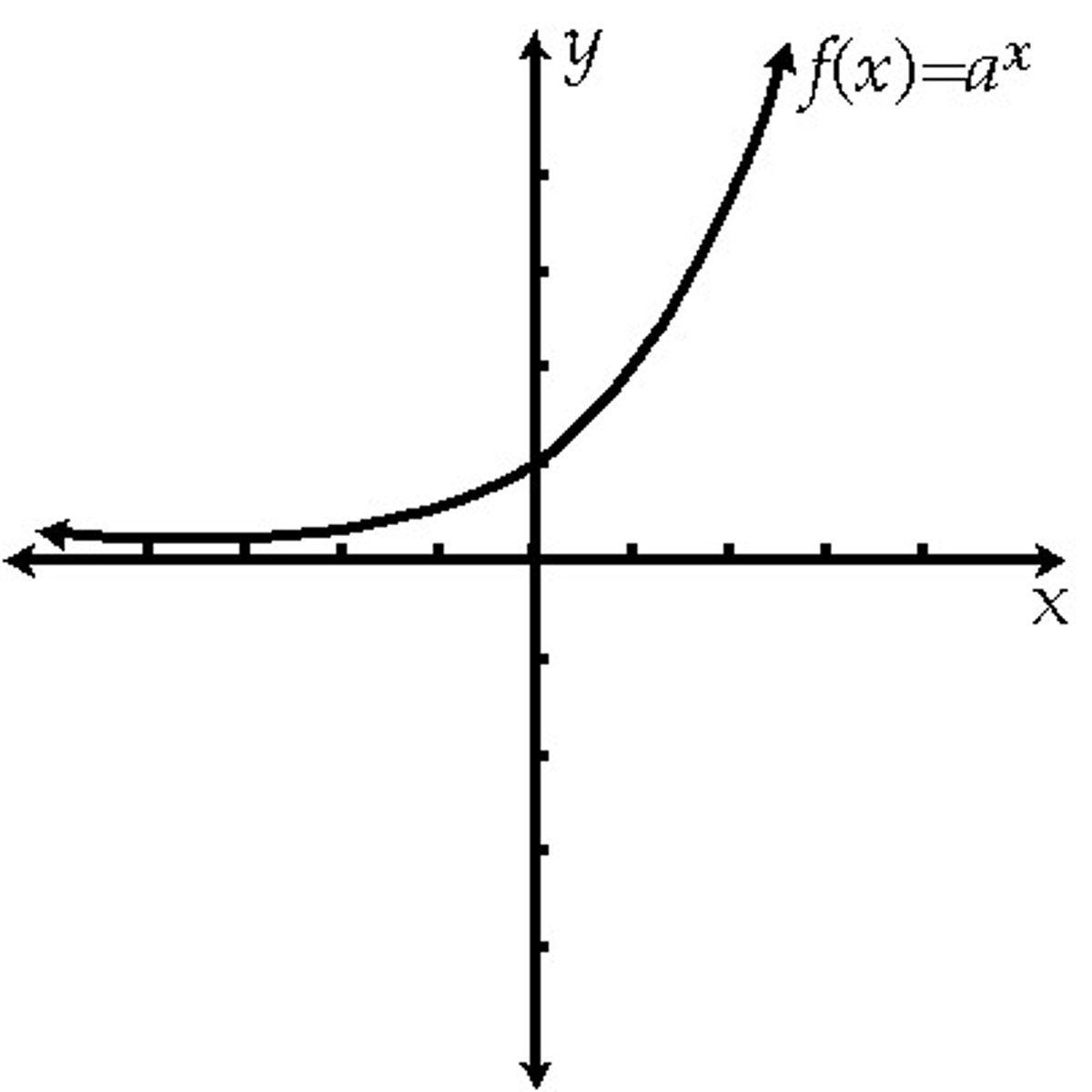
Exponential

y = e^x

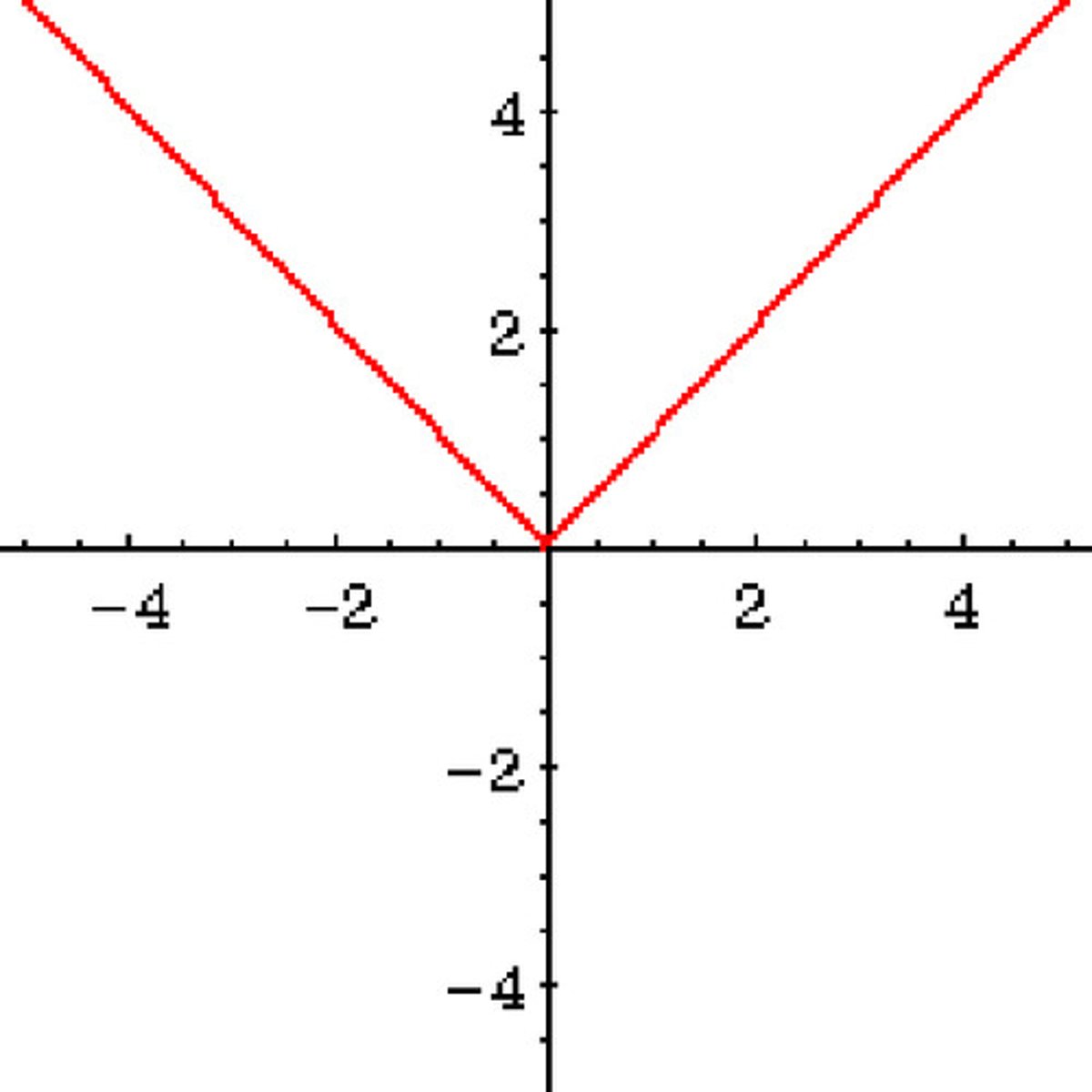
Absolute Value

y = |x|

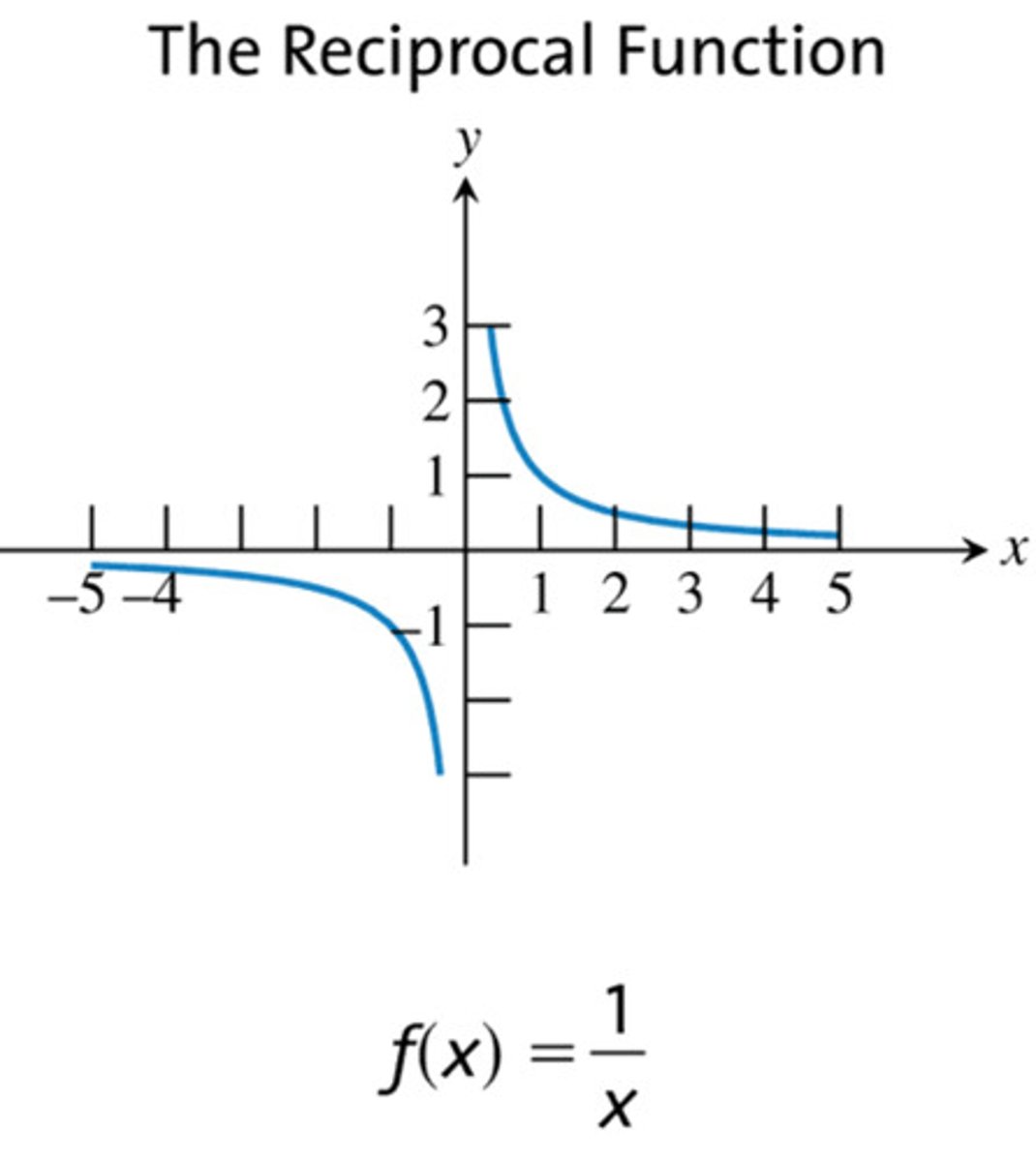
Reciprocal

y = 1/x

Square Root

y = square root(x)

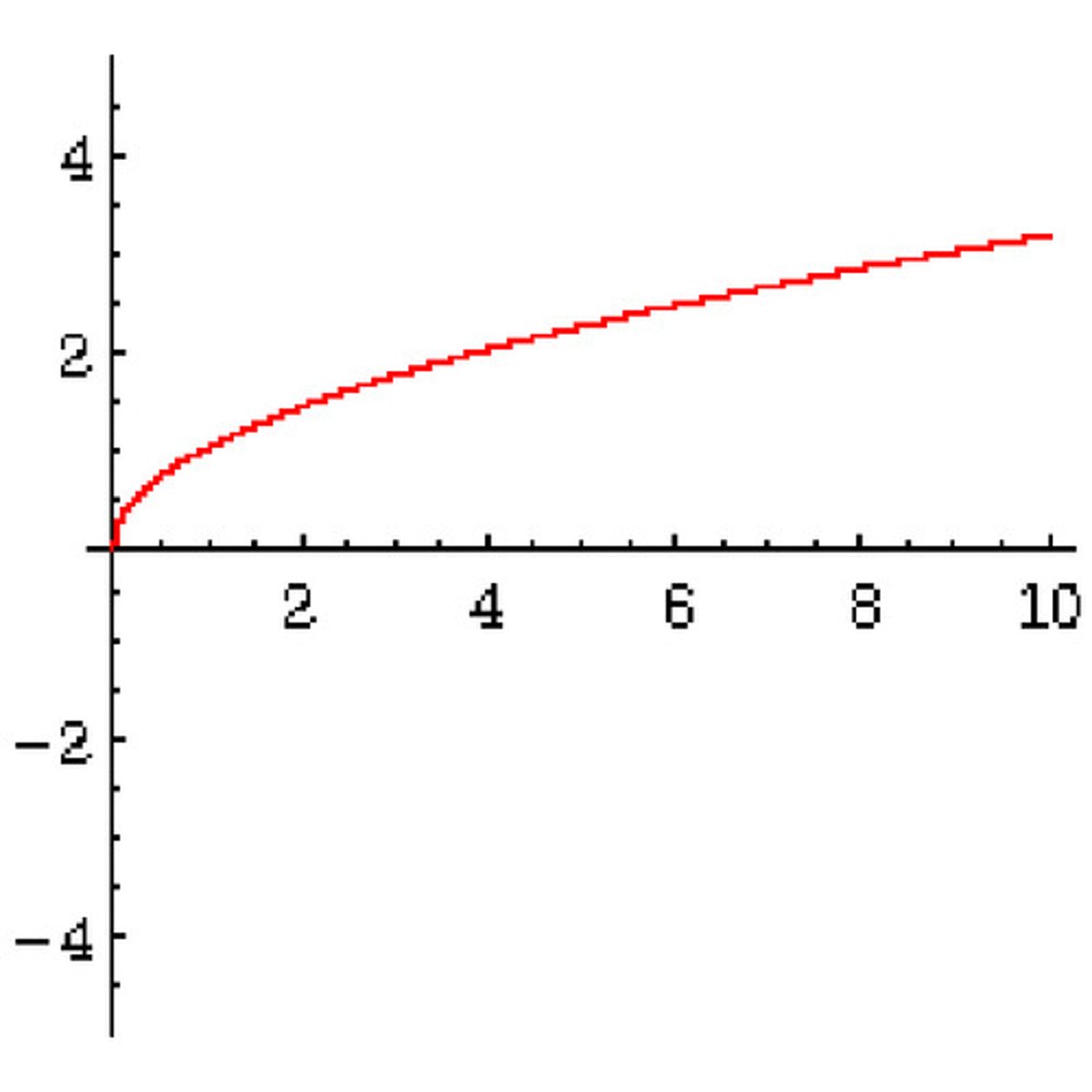
Logistic

y = 1/1 + e^-x

Greatest Integer

y = [x]

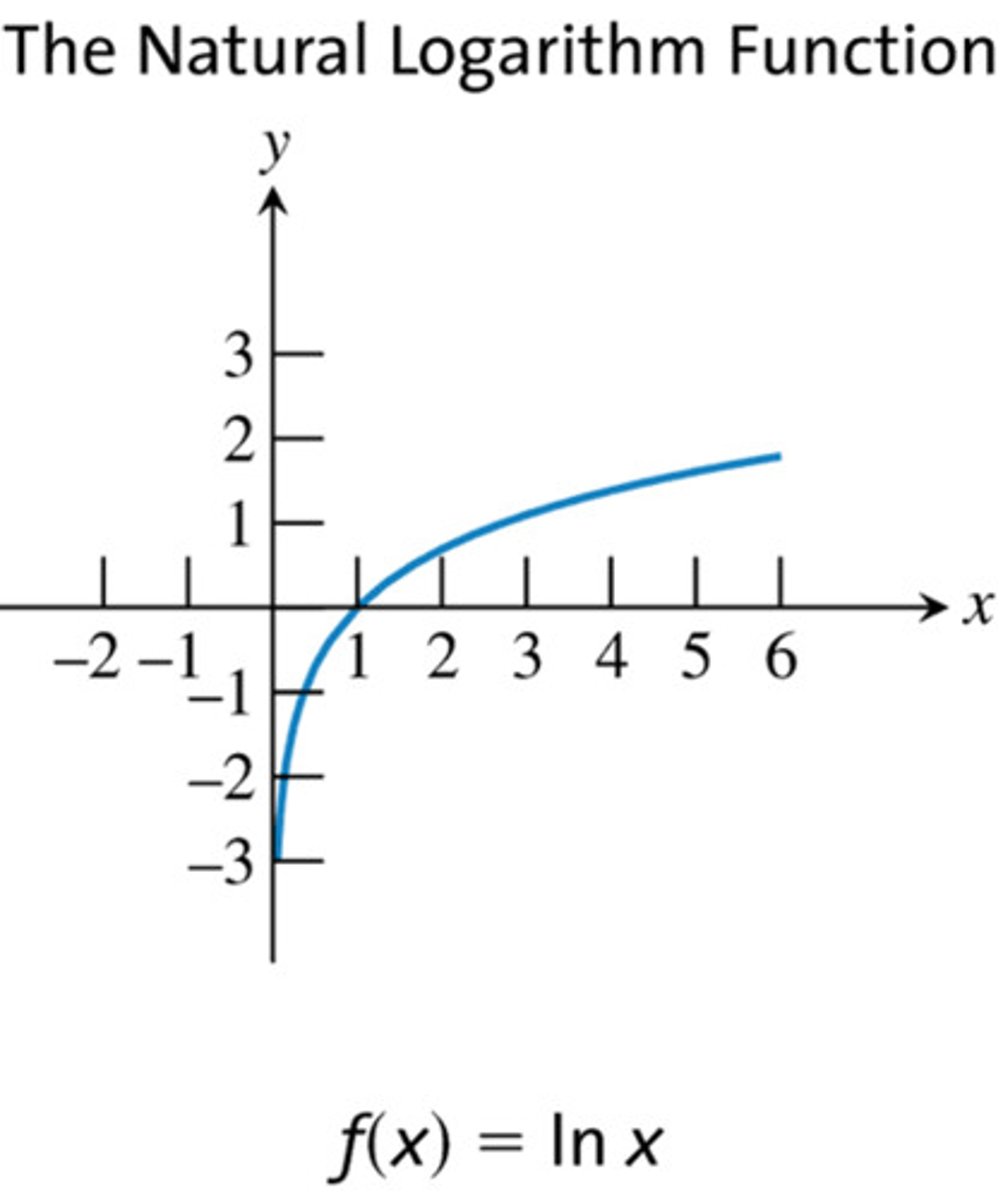
Natural Log

y = ln x

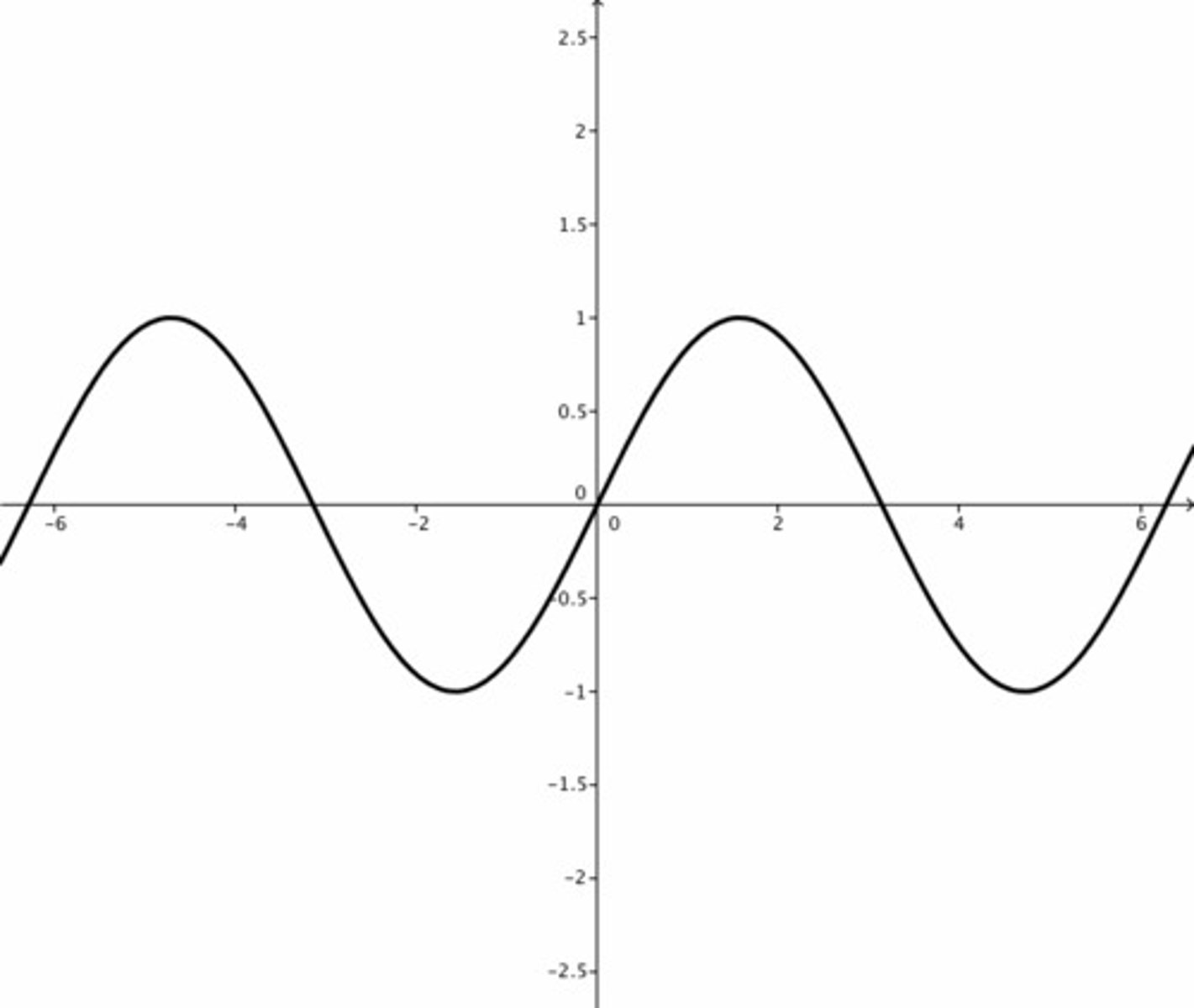
Sin

y = sin x

Cosine

y = cos x

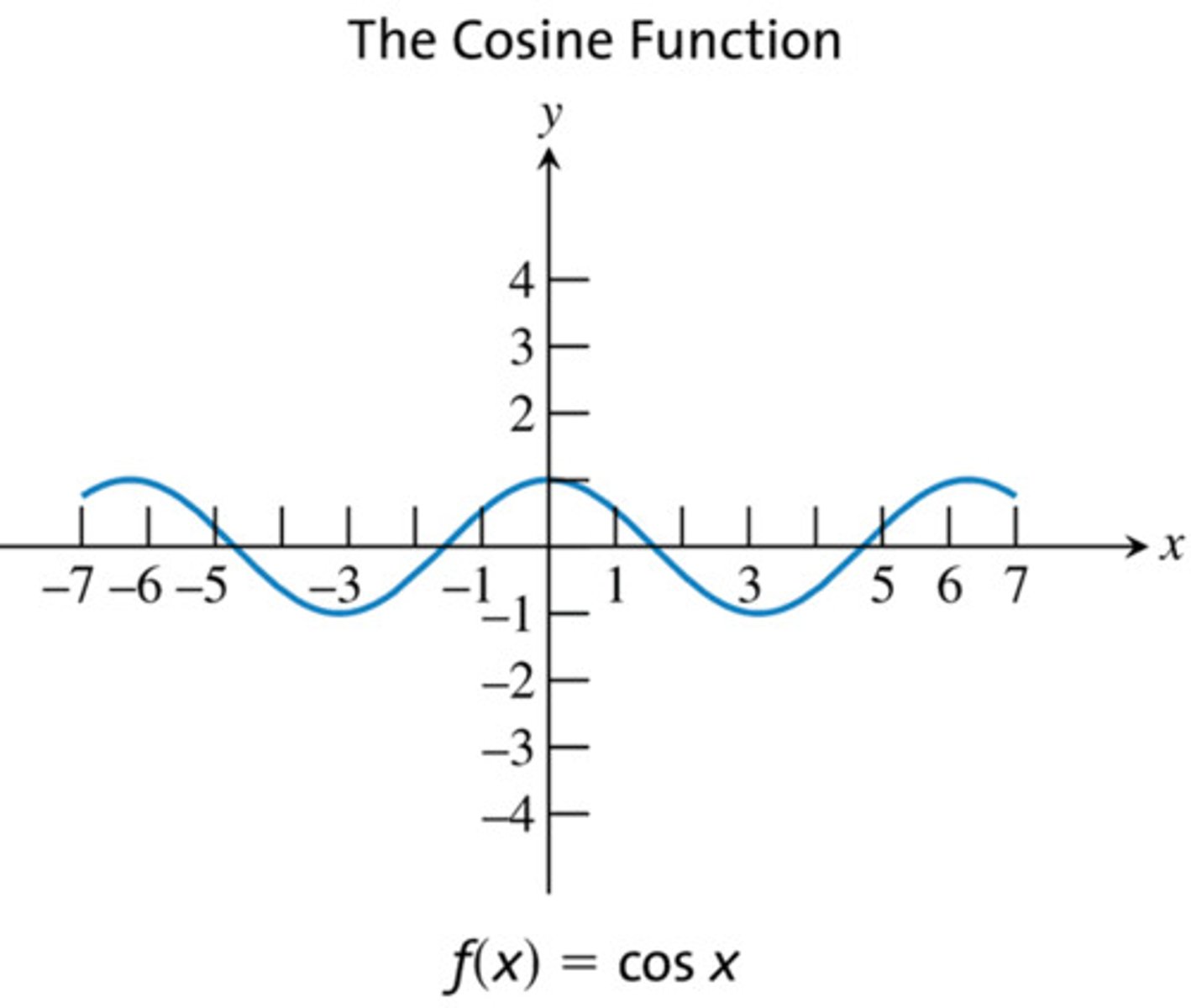
3 functions that don't

have all real numbers as domain

Square root, natural log, reciprocal

Domain (-infinity, 0) U (0, infinity)

Reciprocal