option D: astrophysics

making degrees more smaller

making degrees more smaller

• 1º = 60’ (minutes of arc)

• 1’ = 60’’ (seconds of arc)

• 1º = 3600’’

parallax

• the apparent shift of a near star compared to the distant stars over a period of time

• a star will look like it has moved backwards and forwards throughout the year

• really it is Earth that has moved which changes the perspective from which we look

• other stars will look like they haven’t moved because they are so far away

angle of parallax and finding it

• angle of parallax is measured in seconds of arc, is it is 1’ the distance is one parsec

• further away = smaller angle of parallax

• distance between earth’s position in June and in December is 2R, p = parallax angle

• the distance to the star is Tanp = R/d therefore d=R/tanp

• using small angle approximation:

• tanp = p therefore d=R/p (when the angle is measured in radians)

finding distance in parsecs

when these distances are too approximate

d(parsec) = 1/p (arc-second)

angles smaller the 1/100 arc seconds are too small to measure accurately so distances farther away than about 100 parsecs are too approximate to be useful

luminosity

stars are assumed to radiate like black bodies (emissivity =1), equation is P=eσAT^4

luminosity = power of a star

L=σAT^4

• power

• efficiency

• σ — constant

• area — can be written as area of a circle (stars are spheres but we see circles)

  • L=σπR^2T^4

• temperature

combining brightness and luminosity equations

surface are of a sphere = 4πR^2

brightness is the power per unit area received at a distance from the source

b=L/4πR^2

luminosity cannot be directly measured but it can be calculated from brightness and distance found using parallax

combining the two formulae (not in data booklet)

b=σAT^4/4πd^2

• d = distance from us to star

stellar spectra and Wien’s law

stellar spectra — below 400nm = ultraviolet radiation at a hotter temperature

Wien’s law — λmaxT = 2.9x10^-3 mK

• because the product is a constant λ and T are inversely proportional

the smaller the maximum wavelength, the greater the temperature

classifying stars based on temperature

stars are separated into classes based on their temperature

• hot to cold = O, B, A, F, G, K, M

• our sun is class G

• the hottest stars are blue and the coldest are red

Hertzsprung-Russell (HR) diagram

• stars age following the main sequence from top left to bottom right

• temperature is measured from highest to lowest — pay attention to the axes

• L star/L☉ is used for the y axis, ☉ represents the sun, ratio of Lstar to L☉

• y axis is exponential

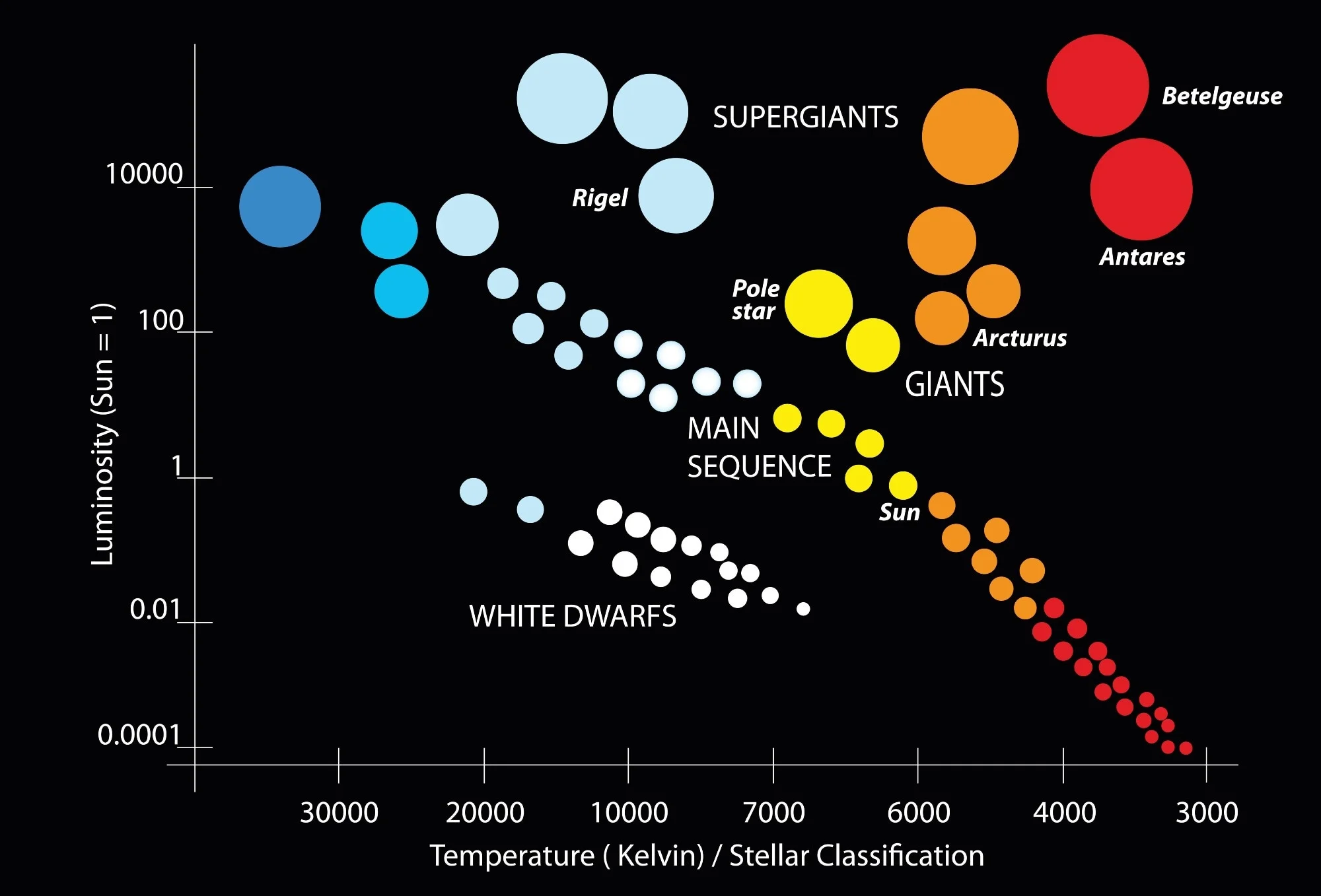
brightness and luminosity of the super giants, relative to the sun

why there aren’t super giants in the bottom left of the HR diagram

• super giants have to be incredibly big to be brighter than the sun given the equations for brightness and luminosity

• no super giants in the bottom left corner because the temperature is too high (relative to the luminosity), we don’t see objects of that temperature in the universe

linking luminosity and mass for main sequence stars

for stars in the main sequence the luminosity and mass (M) of the star can be linked

L=σAT^4

A=4πR^2

L∝R^2

L∝M^3.5

• 3.5 comes from the exponent for the main sequence gradient

• the gradient is not negative because the x axis goes from high to low

impact of a difference in mass on luminosity

• a slight difference in the mass causes a huge difference in luminosity

  • a star with a mass 10 times that of the sun will have a luminosity of 10^3.5 times the luminosity of the sun which is about 3200

• stars have different densities

• more luminous stars on the main sequence have greater mass and shorter lives than less luminous stars on the main sequence

single star

A luminous sphere of plasma held together by its own gravity.

binary star

two stars orbiting a common centre

black hole

A singularity in space-time.

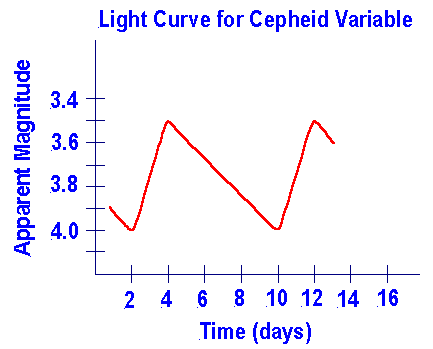
cepheid variable

A star with a period of varying luminosity. The luminosity can be determined from the period and along with the apparent brightness can be used to determine the distance of the star from Earth.

cluster of galaxies

Two or more galaxies that are close enough to each other to affect each other through gravitation.

constellation

A pattern of stars visible from Earth that are not gravitationally bounded.

dark matter

Matter in galaxies that are too cold to radiate. Its existence is inferred from theoretical physics rather than direct visual contact.

galaxies

stars, gas, and dust held together by gravitational forces.

main sequence star

A normal star that is undergoing nuclear fusion of hydrogen into helium.

neutron stars

A very dense star, consisting only of uncharged neutrons

nebula

A cloud of dust, hydrogen, helium and other ionized gases.

planet

 A celestial body that orbits a star.

planetary system

Gravitationally bounded non-stellar objects in orbit around a star or star system.

planetary nebula

The ejected envelope of a red giant star.

stellar clusters

A group of stars gravitationally bounded together.

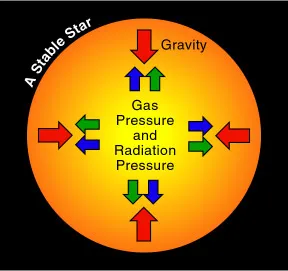
the stability of a star

• depends on the equilibrium of opposing forces

• forces = gravitational, gas and radiation pressure

• equilibrium gained through nuclear fusion which keeps the star hot

cepheid variables graphed

apparent magnitude of luminosity vs time

stellar evolution for less than 1.4 solar masses (solar mass of the sun = 1)

• star stops fusing at about oxygen as the amount of energy released decreases

• planetary nebula occurs (big explosion)

• outer layers of the star blow away (gravity does not keep them together)

• the core (leftover) becomes colder and colder, it contracts more and more (gravity)

• electrons behave as a gas in the core and the pressure they generate stops the core from contracting… more from the slide

Chandrasekhar limit

The largest mass a white dwarf can have is about 1.4 solar masses.

• electron degeneracy prevents further collapse of the core provided that its mass is less than about 1.4 solar masses

• the star will become a stable white dwarf then a black dwarf

• dwarf = no fusion = dead star

Oppenheimer-Volkoff limit

the largest mass a neutron star can have is approximately 2-3 solar masses

• when the mass of the star is 1.4-2.5 solar masses it is a neutron star

• the core will collapse further (due to weight) until electrons are driven into protons forming neutrons

• neutron pressure prevents the star from collapsing further which makes it a neutron star

• neutron stars are heavy because there is no electromagnetic repulsion

when the Oppenheimer-Volkoff limit is exceeded the star becomes a black hole

Hubble’s law

describes the speed at which celestial bodies move away from each other at the present time and changes because the expansion of the universe if accelerating.

v=Hd

• v = velocity

• H = Hubble parameter

• d = distance

using Hubble’s law to find the age of the universe

• using the relationship between speed, distance and time

• the age of the universe is the inverse of the Hubble constant

the cosmic scale factor (R)

a function of time which represents the relative expansion of the universe.

This may be represented by

where d(t) is the proper distance at time t, d0 is the distance at time t0, and a(t) is the cosmic scale factor.

Astrophysicists would out the cosmic scale factor using Einstein’s theory of general relativity laws.

Doppler effect in galaxies

• light has a longer wavelength than when it was originally emitted

• red shift (z) = unitless measure of the speed of an object as a proportion of the speed of light

• change in wavelength due to velocity

• galaxies rotate so light is doppler shifted

• the radiation from the side approaching the earth is blue shifted and the radiation moving away from the earth is red shifted

velocity of recession

Hubble constant

velocity of recession = Hubble constant x distance

Hubble constant has units of k ms^-1 Mpc^-1

V=H₀d

z=H₀d/c

d=cz/H₀