Unit 4 - Work, Energy, Power and Calculus

What is the definition of Work done by a constant force?

What is Work’s quantity, symbol, and UNITS???

Def: When a force F causes an object to be displaced by an amount d, the work done by F is equal to the dot product of F and d.

—> W = F⋅d = Fdcosθ

• Work is a SCALAR (work can be NEGATIVE!!!)

• Units = JOULES

• Symbol is just W

What are the 3 different relationships for Work?

1. W = Fdcosθ (no cosθ if its not angled, cos 0 or 180 = 1 and cos 90 = 0 hence why upward force produces 0 work)

2. W = ΔKE

3. W = -ΔU

What are the 3 different directions of work, and what would work be in each?

Angle for Work is determined with the angle between the applied force and direction of motion 🤯

1. Work to the right with an angle 0 <= θ <= 90

   1. W > 0

2. Work directly upwards (cos90 = 0)

   1. W = 0

3. Work to the left with an angle 0 <= θ <= 180

   1. W < 0 (WORK CAN BE NEGATIVE!!!)

What kind of work with friction ALWAYS produce?

Friction will ALWAYS produces a NON CONSERVATIVE FORCE = negative work

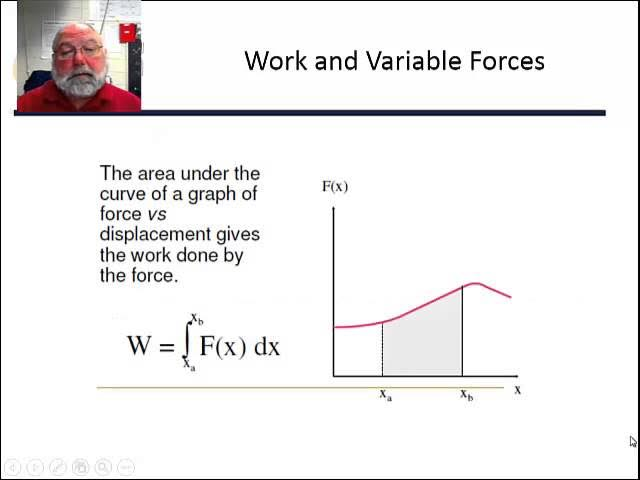
What is the formula for Variable Work?

Look at picture

x_{a =} x_i

x_b = x_f

What MUST you remember about the derivatives and integrals of e, and ln?

The derivative of y = e^x does NOTHING

• the derivative of e^g(x) just means power rule —> = g’(x)e^g(x)

The integral of e^x does nothing but remember +c

|

The derivative of y = lnx is just y’ = 1/x (inverses anything)

• The derivative of ln(g(x)) is CHAIN RULE beacause ln is a function!!!!

The integral of 1/x is ln |x| + c (ABS VALUE!!!)

What is Hooke’s Law?

Hooke’s Law: The force exerted by a spring (F_s) is directly proportional to the extension or compression of the spring. (Spring gives Opposite reaction force to force applied on it)

F_s = -kx

(k = spring constant, x = disp, units are Nm)

In Hooke’s Law, when will F_s be pos and neg? Why?

F_{s =} force of spring = -kx

F_s is positive when you compress the spring cus x is negative

F_s is negative when you pull the spring cus in F_s = -kx, x is positive

How do you model the Hooke’s Law equation with calculus?

Why does the negative go away?

the reason why the negative disappears is because the the work of the spring is OPPOSITE to the work it takes to affect the Hooke’s Law Eq.

THINK:

The applied Work we give affects the equation F = -kx

—> the Work of the spring is the opposite of resulting Spring Force created by the Force we put in

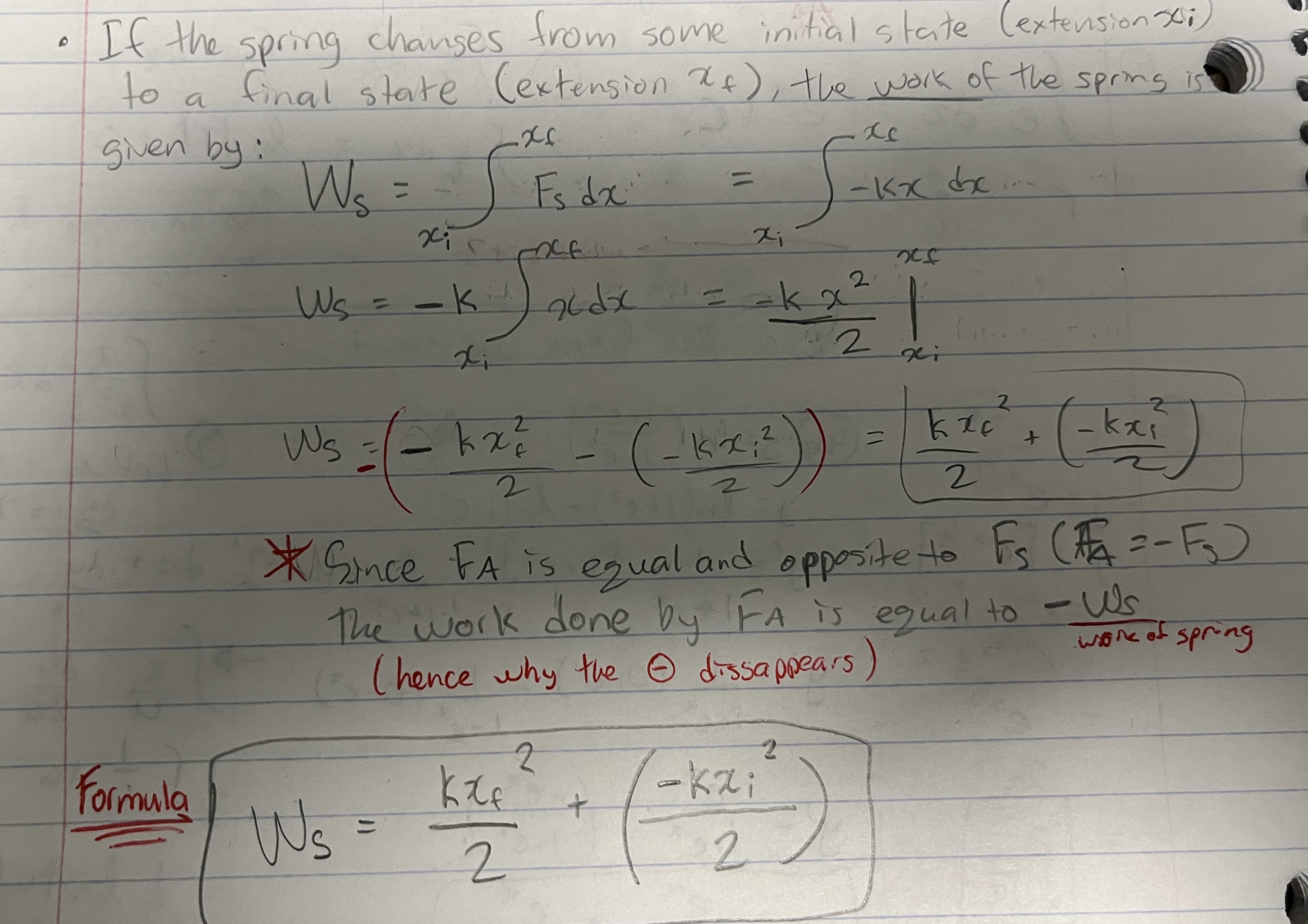
What is Linear Mass Density?

We know that P = density = m/v

For Linear Mass Density, we have the symbol as lambda, and if the mass is distributed along length L, then λ = M/L (units are kg/m)

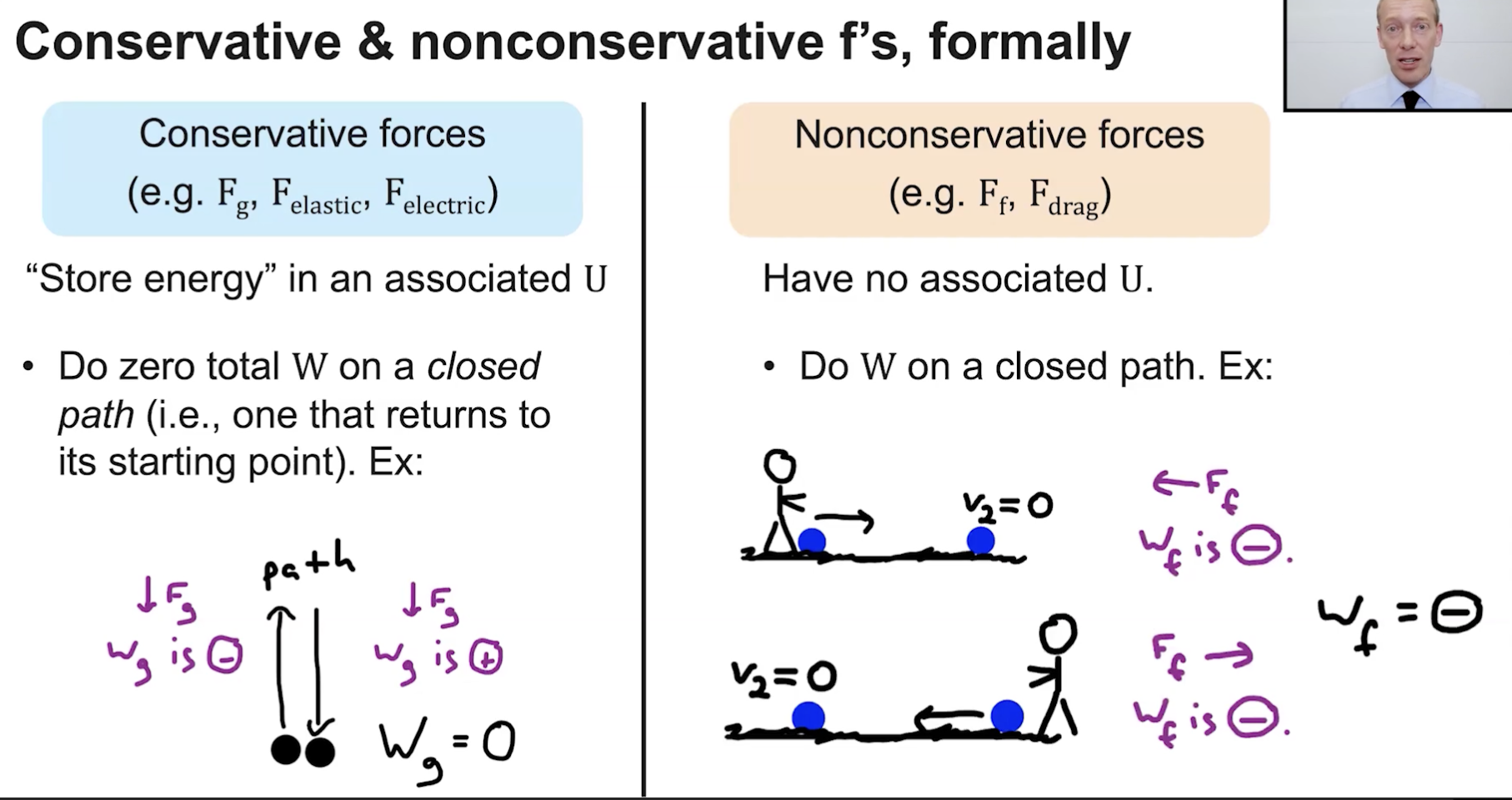
What is a Conservative Force?

What is a Non-Conservative Force?

What is F_net in terms of Conservative and Non-Conservative Forces?

Conservative Force = A force where the work done by it is independent of path (no matter what path, same Work produced)

—>

Non-Conservative Force = A force where the work done depends on the path (basically any force that causes a loss in KE like friction, heat, sound, drag)

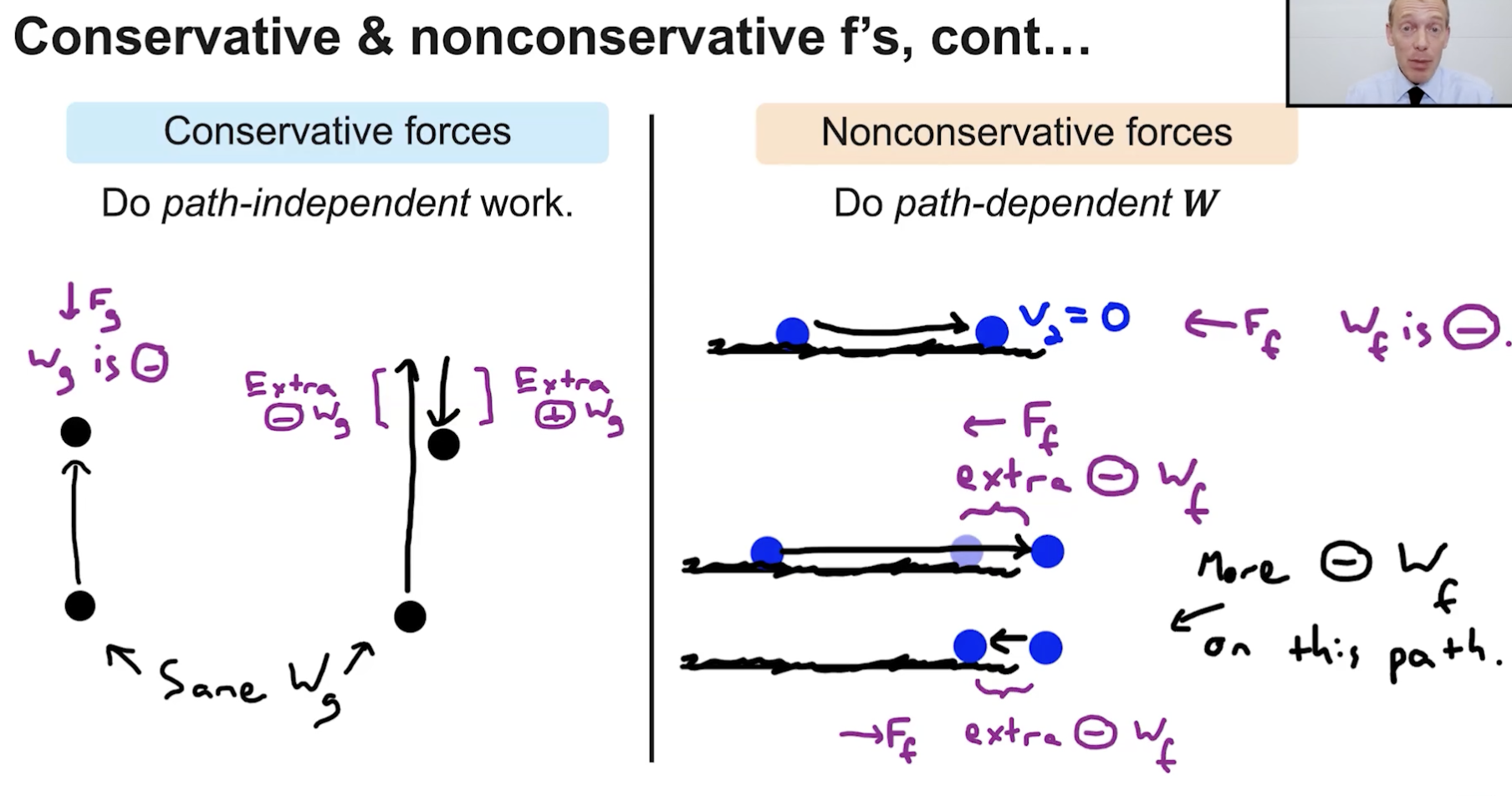
What is something important to know about Conservative and NC forces on a closed path (0 initial speed, speeds up and then ends at 0)

Conservative Forces will do 0 total work in a closed path

NC Forces will ALWAYS do some sort of work even on a closed path

What is Gravitational Potential Energy? (def, magnitude, symbols, formula)

What is Elastic Potential Energy? (def, magnitude, symbols, formula)

Gravitational Potential Energy = Energy associated with the position of a mass in a gravitational field G

• Scalar

• Symbols are PE or U

• ΔU_g = -W_g = - (-mgh) = mgh

Elastic Potential Energy = Energy associated with potential energy of a spring

• also Scalar

• Symbol is U_s

• U_s = 1/2kx²

What is the Conservation of Energy?

In a closed isolated system, there is no change in energy (ΔE = 0)

What is the mechanical energy of a system (E)?

What are the 4 formulas attached to it?

Mechanical energy of a system (E) = the sum of the kinetic and potential energies in a system

|

1. E = KE + U_g + U_s

2. E_f = E_i (cons of energy) (if we lose energy due to NC force, we say E_f = E_i - NC)

3. W_NC = ΔE = E_f - E_i

4. KE_i + U_gi = KE_f + U_gf

What are the 2 ways to find KE_f using Force and Distance?

1. Use W_net = ΔKE

This will then turn into F_net d = KE_f - KE_i

This will then turn into F_netd = KE_f

Now plug in your values for F and d

2. Use ΔE = W_nc 

This will give (KE_f +U_f) - (KE_i - U_i) = F_netd

this will become KE_f + U_f + 0 = F_net d

What are PE curves?

What are the 2 formulas?

What is the Calculus Formula?

PE Curve is used to analyze the motion of a particle in 1D. We only consider Conservative Forces!

• The 2 formulas are:

• 1. ΔU = -F(X) x ΔX

• 2. F(x) = -ΔU/ ΔX

The CALCULUS Formula in differental form is”

F(x) = -du/dx

—>Given a function u(x), the force acting at some positoin x is equal to the negative of the slope of the U vs X graph. (negative of the derivative)

What are the 3 types of equilibirum points on a PE graph?

1. Stable Equilibrium = typically in a U or bottom of parabola shape part of a function

2. Unstable Equilibrium = at the crest of a function

3. Neutral Equilibrium = at a place where -du/dx or slope = 0

What are bounds and what does it mean to be bounded in a PE Curve graph?

The bounds are the 2 points where the PE graph intersects with the total energy of the system (horizontal line)

|

—> to be bounded means the graph needs to stay within those two intersection points.

How do you find KE using a PE graph?

USE THE RELATIONSHIP: E = KE + U

—> knowing this, we can say KE = E- U

—> For this, use the Y-cord for the E line, and the Y-coord for the PE at a certain x-position

How can you tell if a particle can reach a certain position?

A particle should be able to reach a certain position if it falls within the Y-boundary set by the total system E line. 

—> Anything below the particle will be able to reach it and IF OVER, NEVER POSSIBLE since U CANNOT be more the the Total Energy

What is Power?

What is its mag, symbol, Units?

What is its Formula if F is const vs F is variable (calc)?

Power is the rate at which work is done OR Power is the rate at which energy is transformed

• Power is a Scalar

• Symbol is P

• SI Units is Watts (W) = J/s

|Formulas"|

if F const: P_av = W/Δt or P_av = ΔE/Δt

if F is variable: P_inst = dW/dt or W = ∫P_inst dt

What is the relationship between Power. Force and Velocity?

P_av = W/Δt = FD/Δt

—> This means P_av = FV_av

What is Momentum?
What is its symbol?

What are its Units?

What is its mag?

Momentum (p) is p = mv where p and v are ALWAYS in the same direction

SI units are: kg m/s

Vector

What is Impulse?

What are its units?

What is its mag?

What is its symbol?

Impulse is the product of F_net and Δt OR the change in Momentum

• because impulse can be the product of Force over time its units are always (N/s)

• Vector (has direction)

• Symbol is J even though its basically Δp

What is conservation of momentum?

What is its formula?

In a close, isolated system, there is no change in momentum (it is conserved)

—> gives us a formula: m₁v_1i + m₂v_2i = m₁v_1f + m₂v_2f

What are Oblique Collisions? (Momentum in 2D)

Oblique Collisions are angled collisions. 

• you will add up the components to make a resultant vector, and that magnitude and direction is the final movement

What MUST ALWAYS be remembered with ANY Collision?

What are the 4 types of Collisions?

In ANY collision, momentum will always be conserved!

(This means either the total momentum is equal before/after or lost in thermal or sound)

1. Inelastic

   • KE_f < KE_i (energy lost to thermal energy and sound)

1. Elastic

   • KE_f = KE_i

2. Explosion

   • KE_f > KE_i

3. Oblique

   • P_i = P_f however vector components so add them up

What should you remember about the Center of Mass (CM) of particles?

• You must remember that the CM of a particle MUST be broken down into X and Y maybe even Z components.

• The component summation is similar to the Translational Equilibrium

• CM is also based on the pivot points set by the Q

When do we have to use Calculus for CM?

We will need to use Calculus for SOLID objects or NON- UNIFORM object

|

—> If we have a non uniform rod with a varying density of λ = kx, where k will stay constant

then 

λ = dm/dx

x_cm = 2/3L

What is a differential equation?

A differential equation (DE) is an equation with a derivative.

The solution to a differential equation is a function y= f(x), that when subbed back into DE, it makes a true statement

EX:

dy/dx = 3x² —> integrate this

y = x³ + C

How do you get Terminal Velocity for a DE?

You dont even need to fully create the differential equation.

—> Just set acceleration (dv/dt) = 0 since at terminal velocity it CANNOT accel more

• Then just solve for V