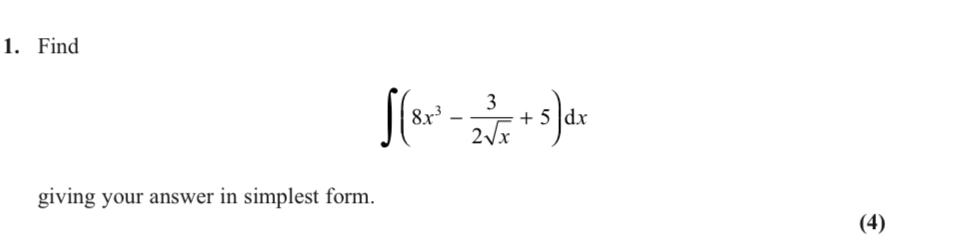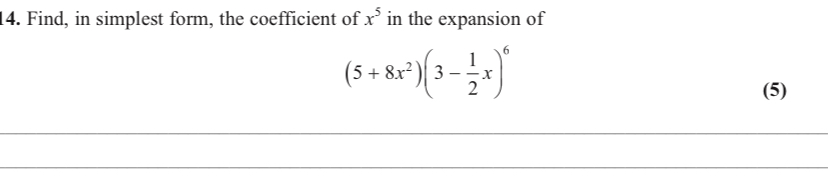AS Maths practice question methods

• the tangent has the same gradient and the same point of intersection as the curve

• Differentiate the equation and sub in x=2 for the x value, find the gradient

• Sub gradient and point into equation of a line and solve for y=mx+c

• Answer = y=20x-27

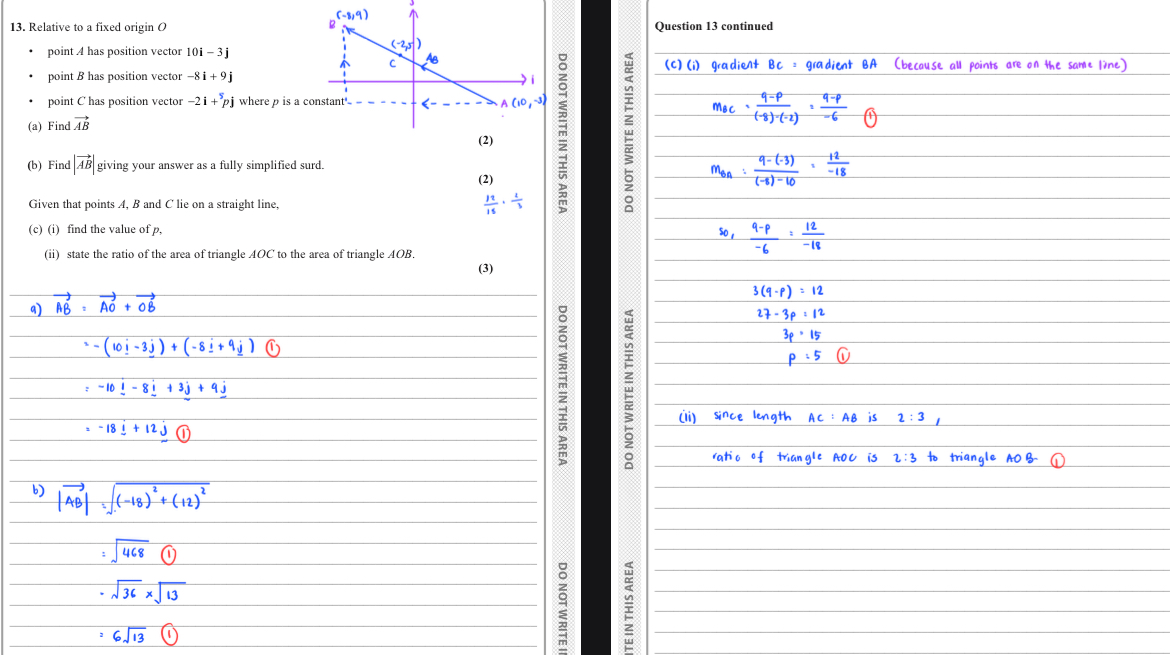
• a) draw a diagram and the angle to find

• Find the direction vector

• Calculate the angle using trigonometry

• Add 180 to find total bearing

• Answer = 246.8

• b) speed is distance over time

• Find distance (magnitude) using direction vector

• Convert time (keep in hours)

• Sub into equation

• Answer = 2.77

• a) rearrange to make x the subject by factorising out x

• Rationalise the denominator

• Simplify fully

• Answer = 6+3[2

• b) change so 2 is the base on either side

• Make powers equal and solve

• Answer = 5/12

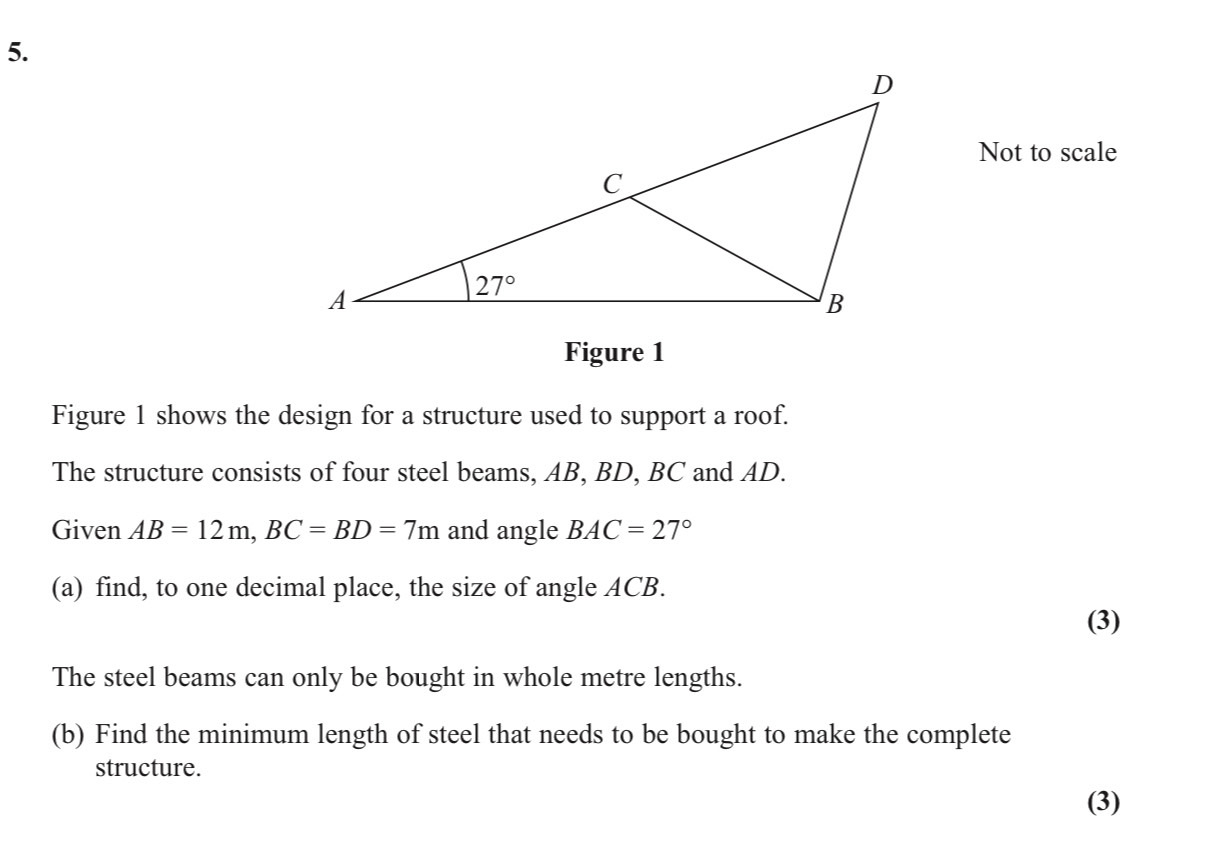
• a) use sine rule to find angle

• Angle found is 51.1, but the angle in question is obtuse

• Use sin rule for second value (180-51.1)

• Answer = 128.9

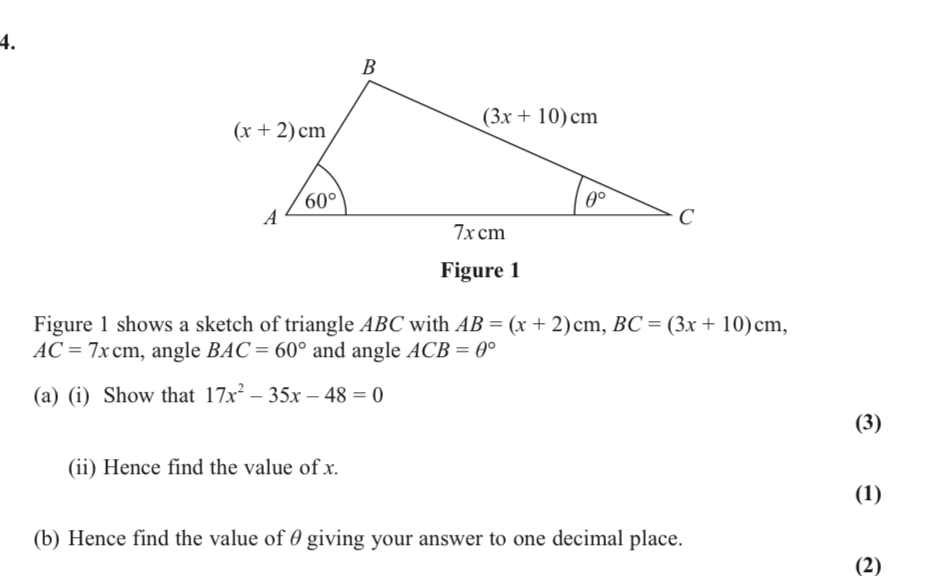
• b) label all sides, use cosine rule to find AD

• Find angle DCB

• DCB = CDB

• CBD = 77.8

• Use to find angle ABD to find total length AD

• Add 12+7+7 to find total length then round up

• Answer = 42m

• a) use binomial expansion

• Answer = 1+10kx+45k²x²+120k³x³

• b) 120k³=30k

• Divide by k. k²=1/4

• Answer= k=+1/2, -1/2

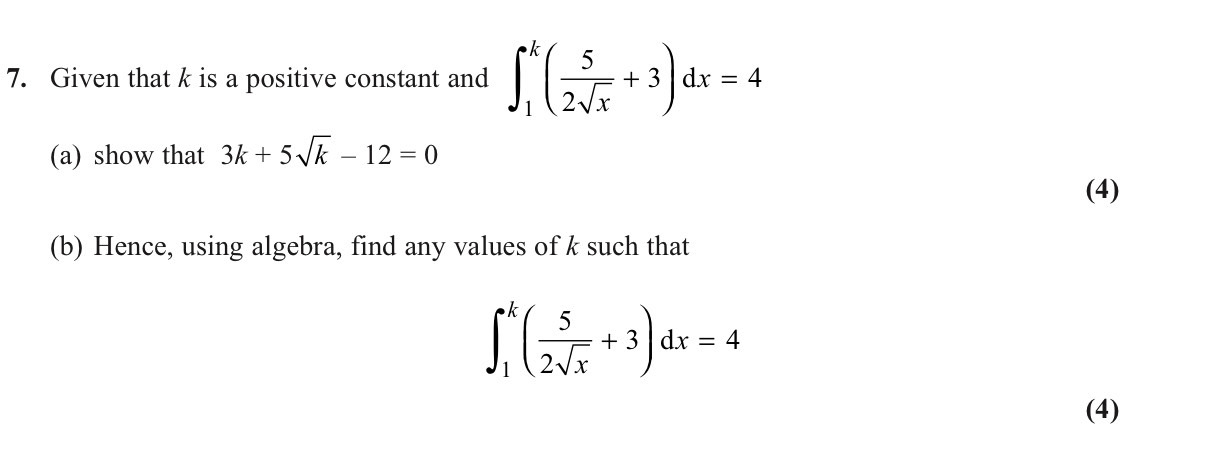
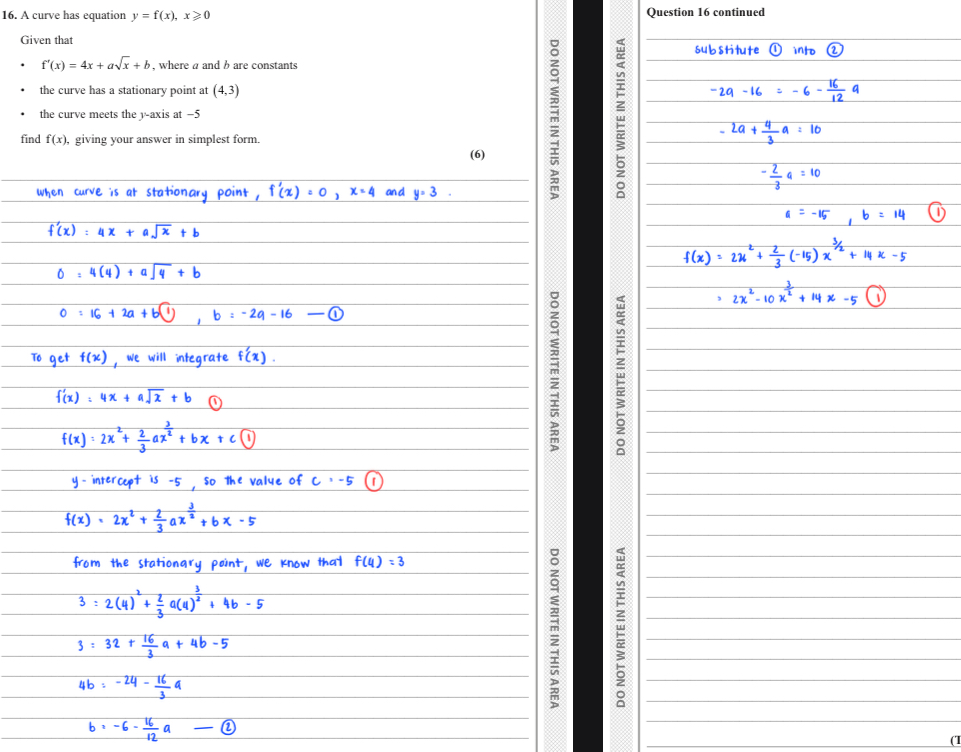
• a) simplify the bracket , =(5/2x^-1/2+3)

• Differentiate = 5x^1/2+3x

• Expand using k and 1 to get 5[k+3k-12=0

• b) sub in x=[k

• = 3x²+5x-12=0

• Expand our algebraically

• (3x-4)(x+3)

• [k=4/3 or -3

• Reject -3, negative root

• k=16/9

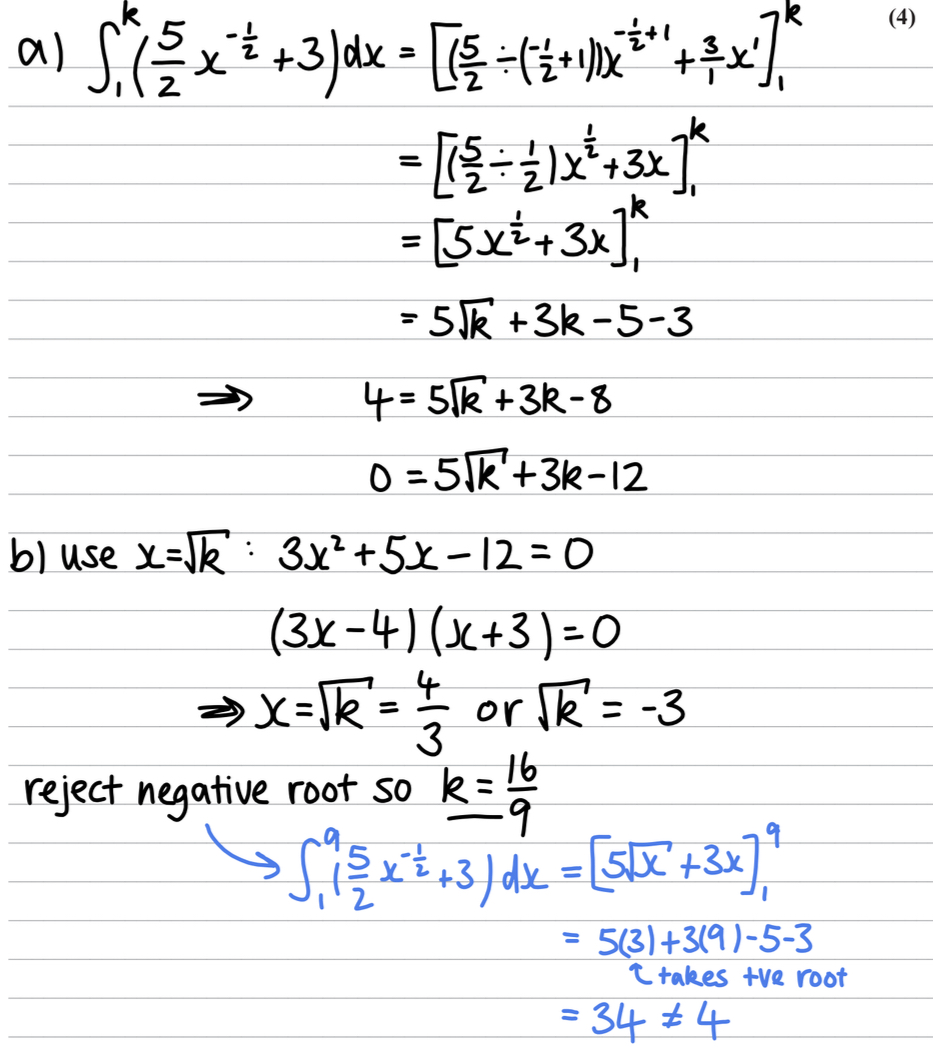
• a) t=0, so e^0 =1

• 65×1 = 65

• So angle = 18+65=83

• Answer =83

• b) 35=18+65e^-t/8

• e^-t/8=17/65

• Take ln of both sides

• -t/8=ln(17/65)

• t=-8ln(17/65)

• answer = 10.7

• c) t is infinite, e^-t/8 is 0

• So 65×0=0

• Answer= minimum temp is 18 degrees which is higher than 15

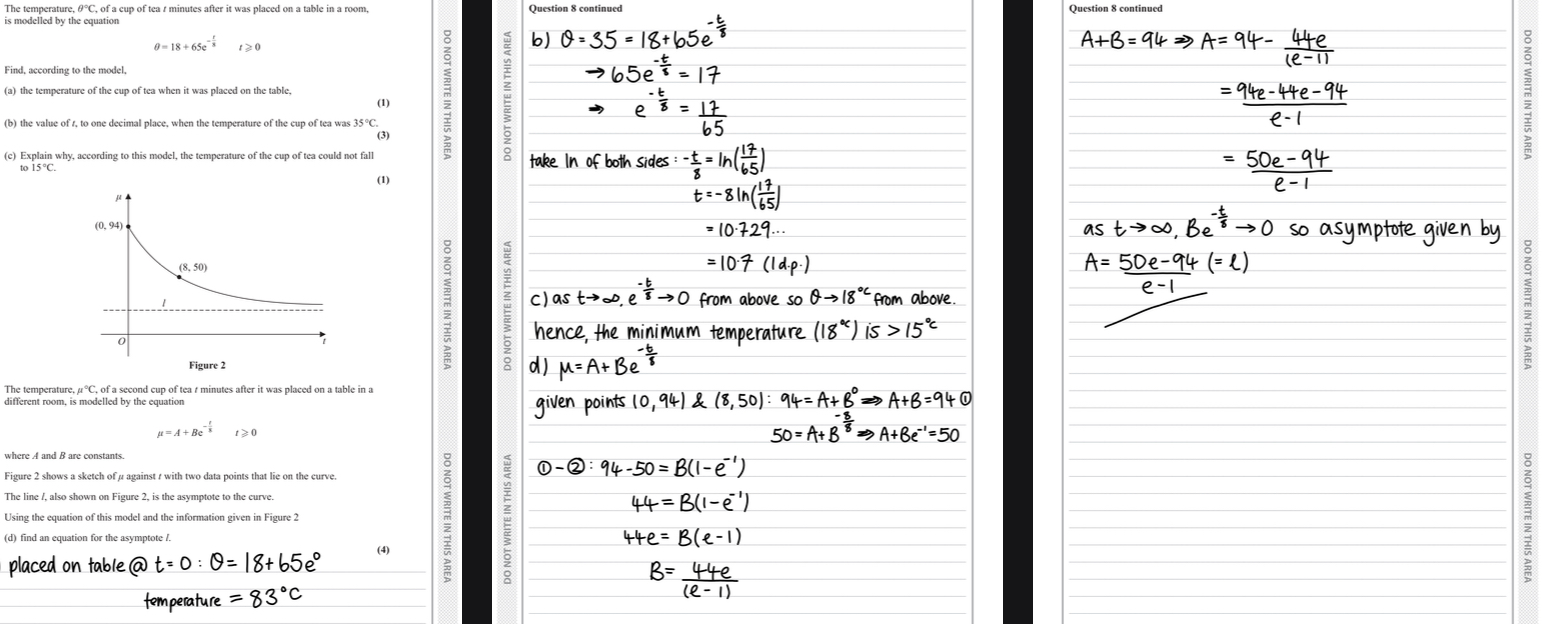
• d) sub points into the equation where x=t and y=u

• Solve using simultaneous equations, form a third equation by using 1-2

• Find B

• Sub into original equation 1

• find A (answer)

• Answer= 5e-94/e-1

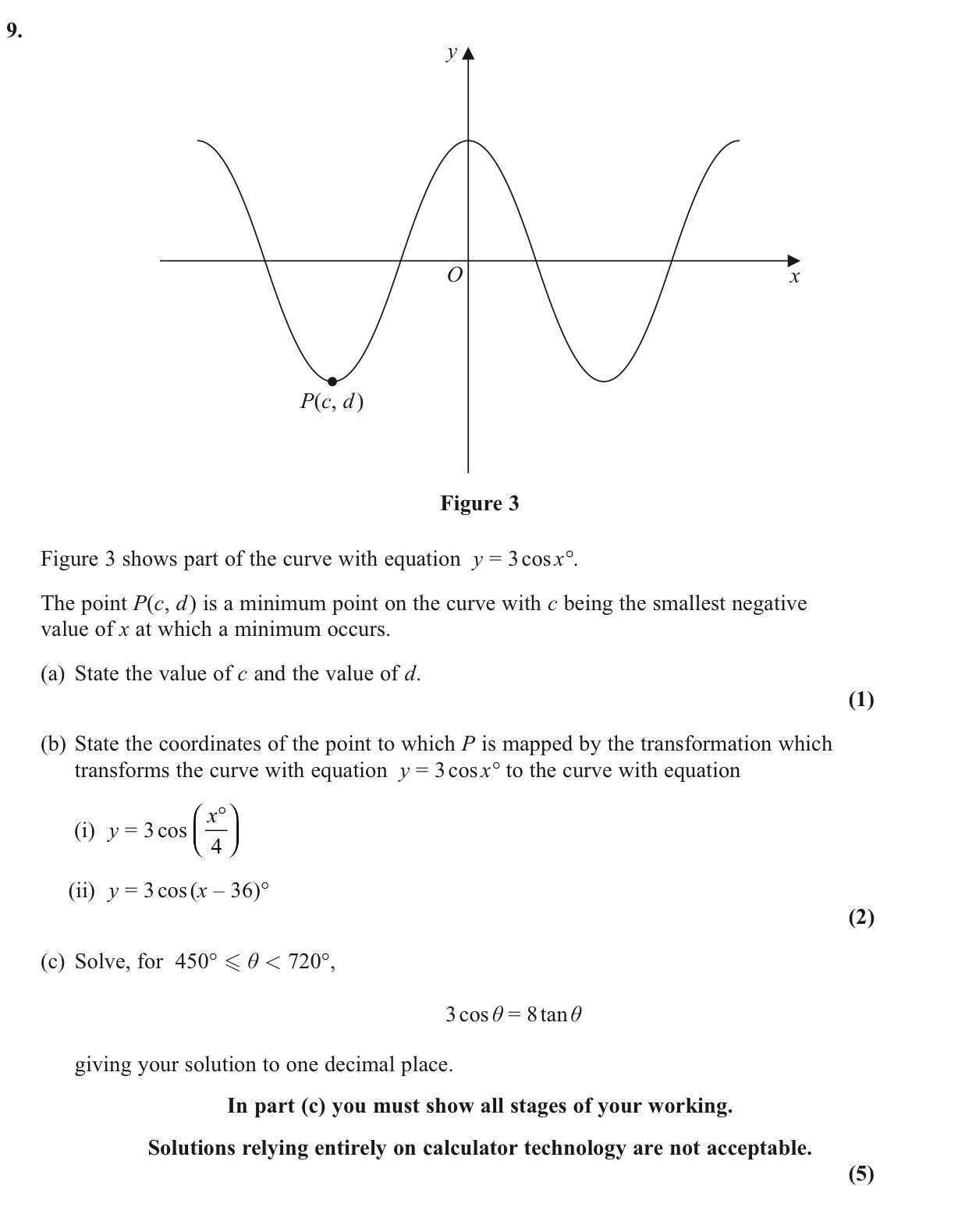
• a) the minimum of cosx=-1

• So the minimum of 3cosx=-3, so y=-3

• P is the first minimum for x<0 so c=-180

• Answer = P(-180,-3)

• b) i) in bracket so effects x

• Times x by 4

• Answer = (-720,-3)

• ii) inside bracket so effects x, x+36

• Answer = (-144,-3)

• c) list trig identities

• Sub in gradient identity and simplify

• Sub in the other trig function cos²0=1-sin²0

• Make into quadratic and factorise

• Reject value -3 as min value is -1

• Use sin0=1/3

• Angle is 19.47

• Find second value using 180-

• Add 360 to find within range

• Answer = 520.5

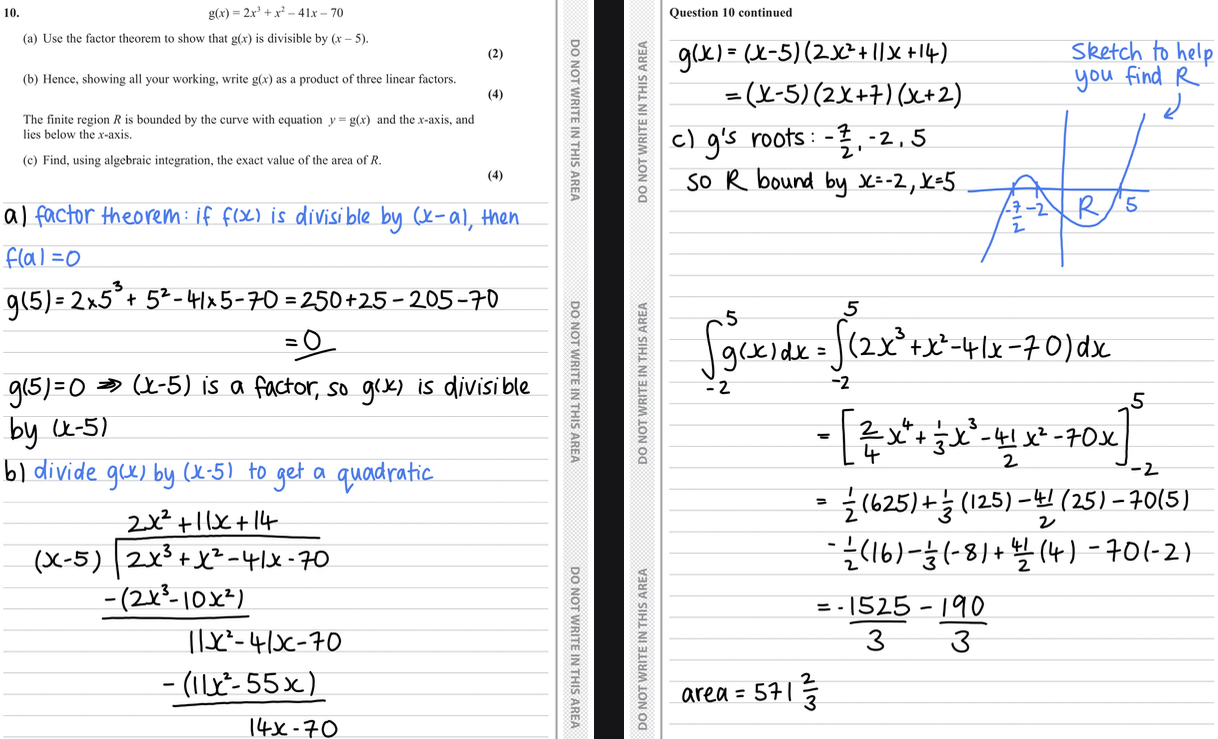
• a) sub x=5 into the equation and solve to prove equals 0

• Make a concluding statement

• Answer = (x-5) is a factor as g(5)=0 so g(x) is divisible by (x-5)

• b) divide using polynomial division ax2+bx+c and x-5

• Find values a b and c

• Write quadratic and sub into calculator to find x values

• Answer = (2x+7)(x-5)(x+2)

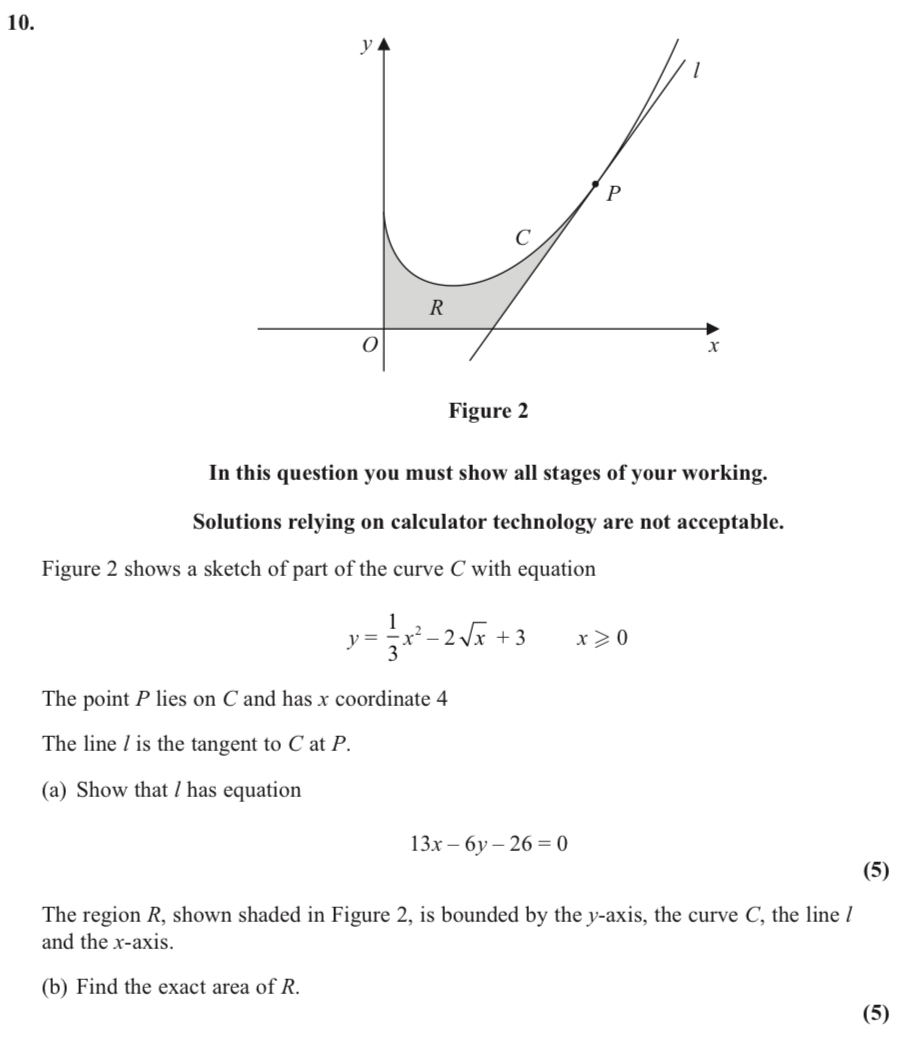
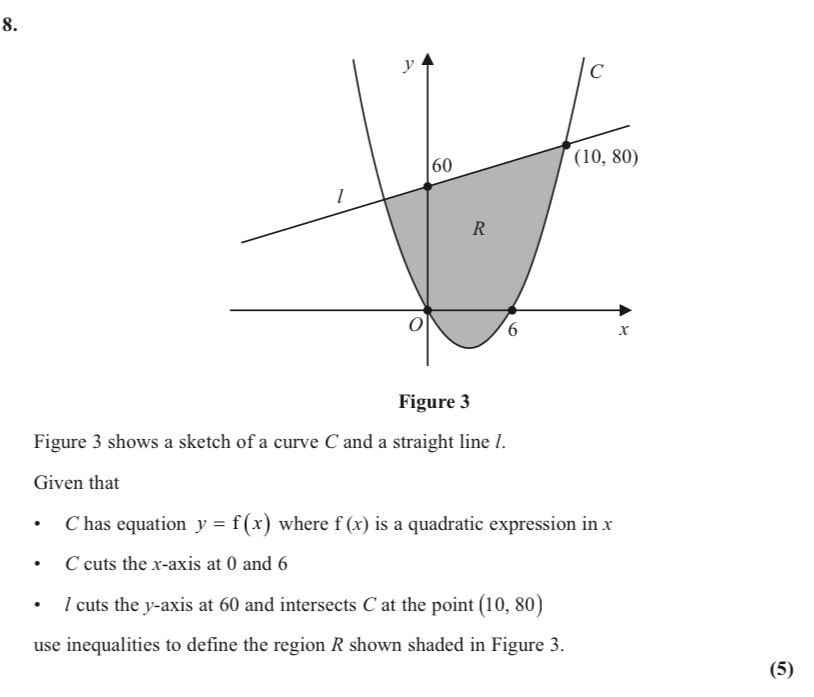
• c) find roots from previous answer and y intercept from equation

• Sketch a graph and label region R

• Integrate the equation

• Sub in 5 and -2

• Calculate (5)-(-2)

• Answer as exact value and +ve

• Answer = 1715/3

• i) expand back out into x and y brackets to find the centre of the circle

• Point (-9,1)

• The radius and tangent are perpendicular so find gradient

• Gradient between (-9,1) and (-5,7) is 3/2

• So gradient if tangent is -2/3

• Sub into equation if a line with point

• In form ax+by+c=0

• Answer= 2x+3y-11=0

• ii) fourth quadrant so need the centre of c2

• Expand new equation out to find point

• Centre (4,-6)

• If it lies entirely in one quadrant it doesn’t cross the axes so the radius has to be less than 4

• r<4 so 52-k<4²

• k>36

• r>0 as lengths can’t be negative so 52-k>0

• Answer = 36<k<52