lec 5 - biostats 1 (gonzalez)

what is statistics?

• science of numberes

• a way of learning from data

• study design heavily influenced by statistical analysis plan

• biostatistics is statistics applied to biological and health problems

basic concepts

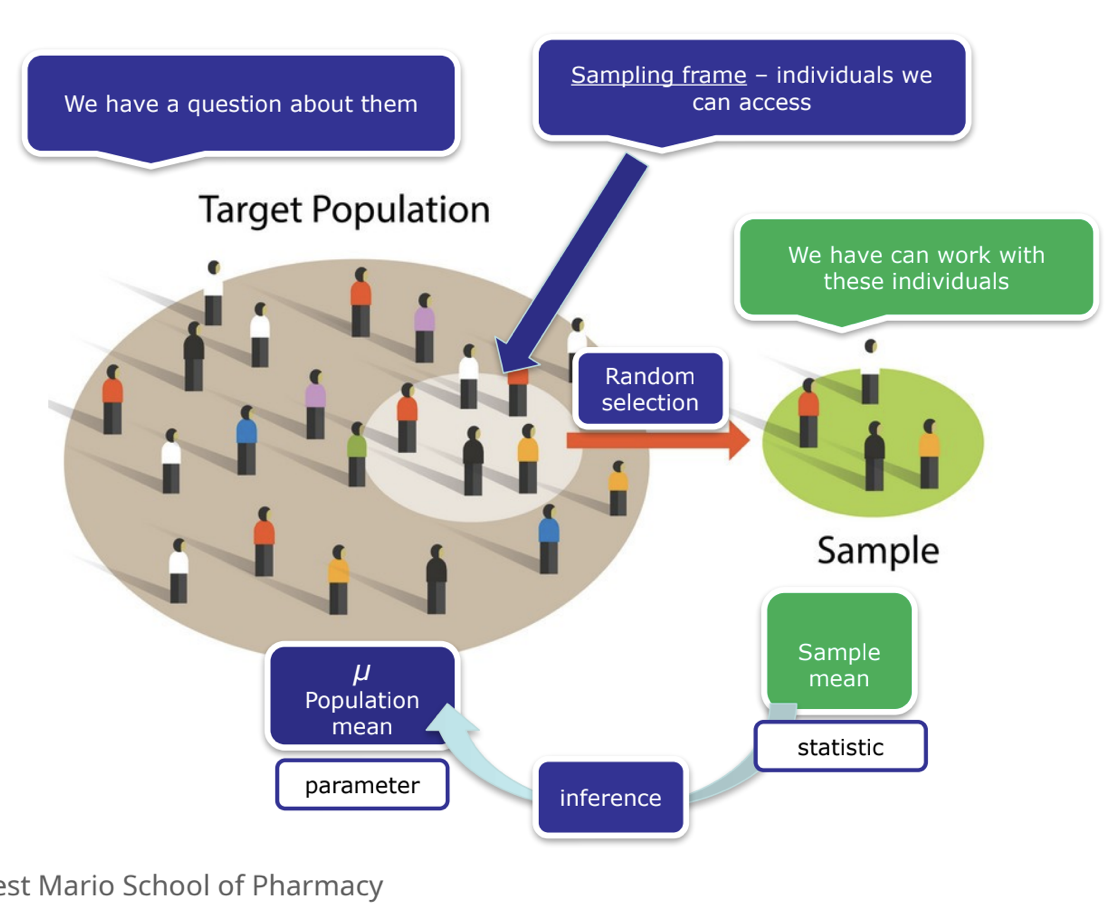
• population

• sampling frame

• sample

  • portion of the population

  • random → each member has an equal change of being picked

• observation

  • the unit upon which measurements are made

• variables

  • characteristics being observed or measured

• value

  • a realized measurement

variables

independent variables (IVs)

• manipulated by the investigators

• example: treatment vs control

dependent variables (DVs)

• also known as outcome or response variable

• example = cured vs not cured

• what we are measuring

confounding variables

• distorts relationship between IVs and DVs

• variable associated with IV, risk factor for DV and NOT an intermediate step between

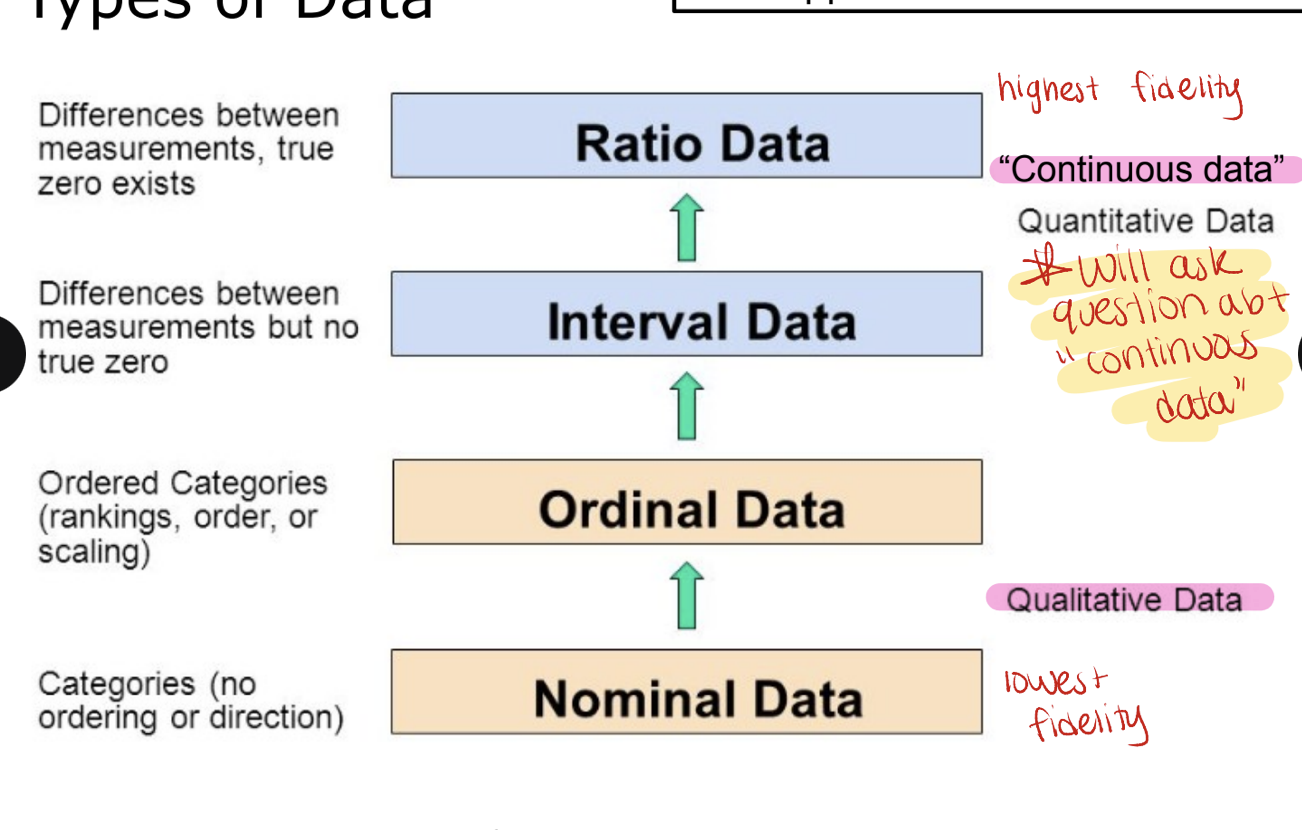
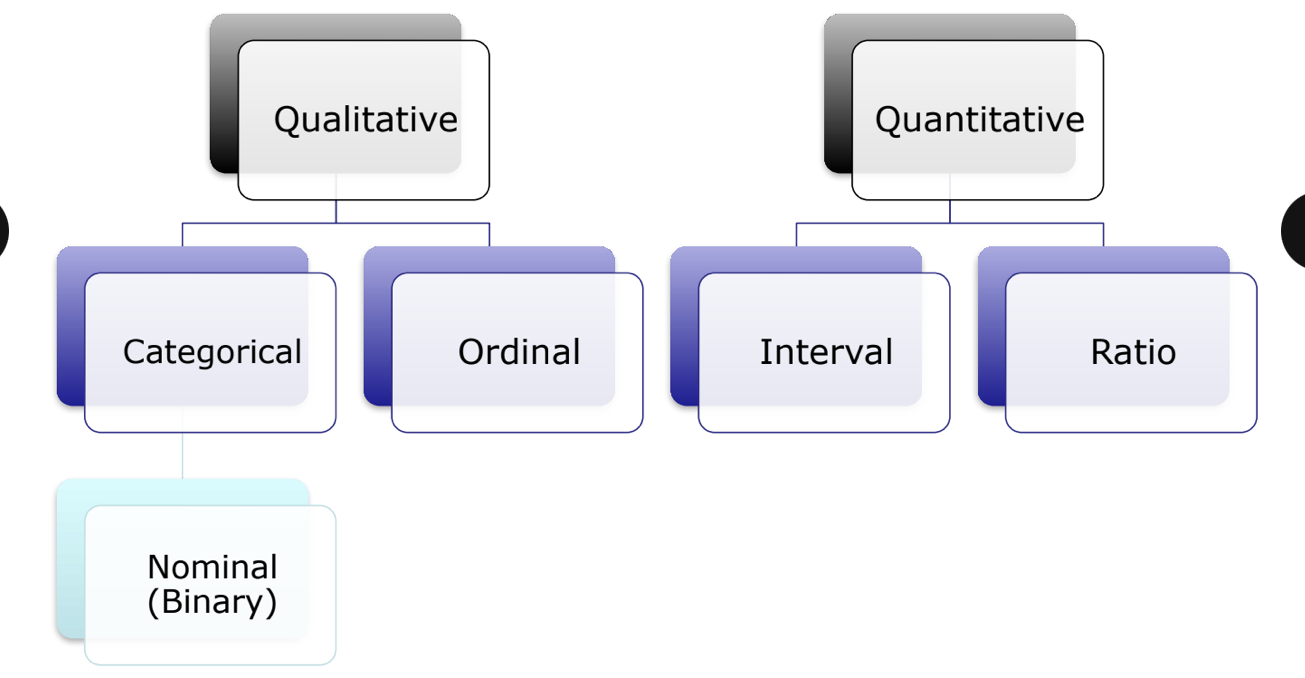
types of data

applies to both IVs and DVs

qualitative data

• nominal/categorical data → categories with NO ordering or direction such as blood type, gender (lowest fidelity)

• ordinal data → ordered categories (rankings, order or scaling) such as pain scale or ranking

quantitative data (continuous data → can take any value within a given range including decimals)

• interval data → differences between measurements but no true zero

  • difference between temperatures is meaningful and consistent (e.g. the difference between 10 and 20 is the same as 20 and 30C) but zero does not mean NO temperature. you cannot say that 20C is twice as hot as 10C.

  • calendar years

• ratio data → differences between measurements, true zero exists (highest fidelity)

  • height/weight → there is a true zero. you can say 100cm is twice as tall as 50cm.

  • age, length/distance

qualitative - categorical/nominal data

• observations are classified into named categories without specific order; mutually exclusive (each observation can belong to one category at a time)

  • yes vs no

  • blood type

  • disease status

• note: some consider nominal = bindary (when there are only 2 options)

qualitative - ordinal data (on exam)

named categories with specific rank orders

• likert style teaching evaluations (strong agree…strongly disagree)

• age group (infant, child, adolescent, adult)

• military rank (private E-1, private E-2…)

quantitative data (on exam)

• can also be classified into interval and ratio data

• interval

  • zero is arbitrary

  • example

    • temperature (F/C)

    • pH

    • clock time (00:00 as midnight)

• ratio

  • zero is clear and meaningful (indicates absence of something)

  • examples

    • enzyme activity

    • dose amount

    • reaction rate

    • flow rate

    • concentration 

    • pulse

    • weight

    • length

    • temperature in kelvin

    • survival time

• note: each can be discrete or continuous but do NOT worry too much about that

data type summary

nature of the independent variable

0

• just one population

1

• 1 IV with 2 levels (groups)

• 1 IV with >2 levels (groups)

• 1 IV that is interval (continuous) in nature

>1

• 1 or more interval +/- or omre categorical IV (with varying # groups)

nature of the IV - example HYVET study (on exam)

study design

• RCT assigning patients 80 y/o or older with SBP 160 mmHg or greater to 1 of 2 groups

  • indapamide

  • placebo

• primary outcome → fatal or nonfatal stroke

independent variable

• medication group (indapamide or placebo)

• categorical/nomial in nature; 2 levels (or groups) → mutually exclusive

independence of the variable

independent samples (unpaired/unmatched)

• 2 separate groups, NO matching or pairing

  • commonly seen in parallel group RCTs

  • can also be more than 2 groups

  • most common study we will see

• key is that each observation is only in one group

  • indapamide → fatal or nonfatal stroke

  • placebo → fatal or nonfatal stroke

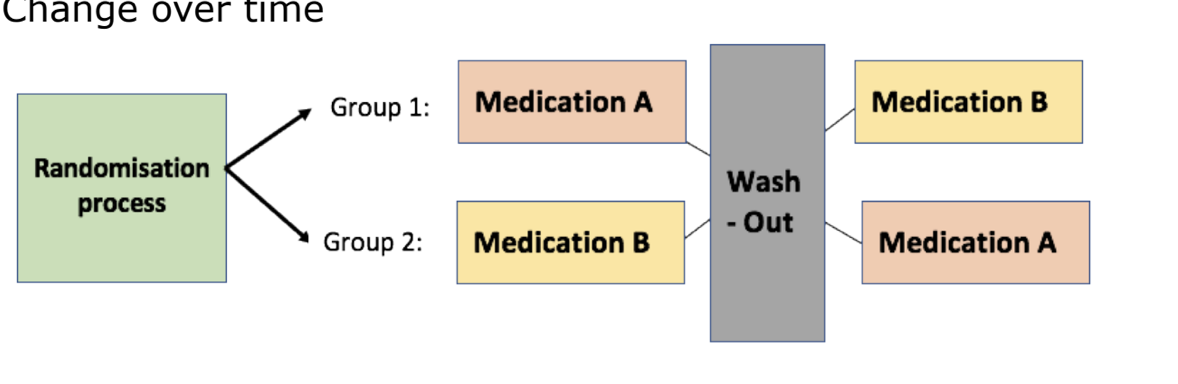
paired samples (matched samples)

• each point in one sample is matched to a unique point in the other sample

• a good example is 1 person with 2 data points

• study designs

  • pre/post test

  • crossover study designs

  • change over time

independence of IV - example HYVET study

study design

• RCT assigning patients 80 y/o or older with SBP 160 mggHg or greater to 1 of 2 groups

  • indapamide

  • placebo

• primary outcome → fatal or nonfatal stroke

independent variable = medication group (indapamide or placebo)

• categorical in nature; 2 levels (or groups)

• independent data → groups were run parallel (no x-over)

measures of central tendency

mean

• mathematical average

• can be calculated for interval and ratio scale data

• mean can be afefcted by outliers

median

• middlemost observation; half of values above/below this point

• can be useful for describing ordinal data

• unaffected by outliers so may be more useful than the mean to describe data when outliers exist or when continuous data are NOT normally distributed

mode

• most frequently occuring observation

• most useful when 2 or more clusters of data exist

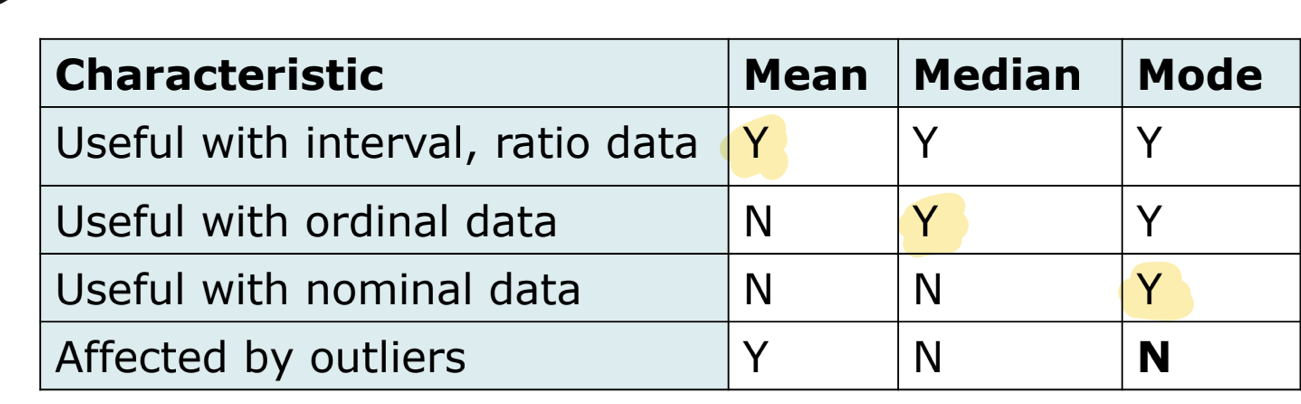
• no single measure of central tendency is best for al situations

  • mean → useful with interval, ratio data

  • median → useful with ordinal data

  • mode → useful with norminal data

interpreting data spread

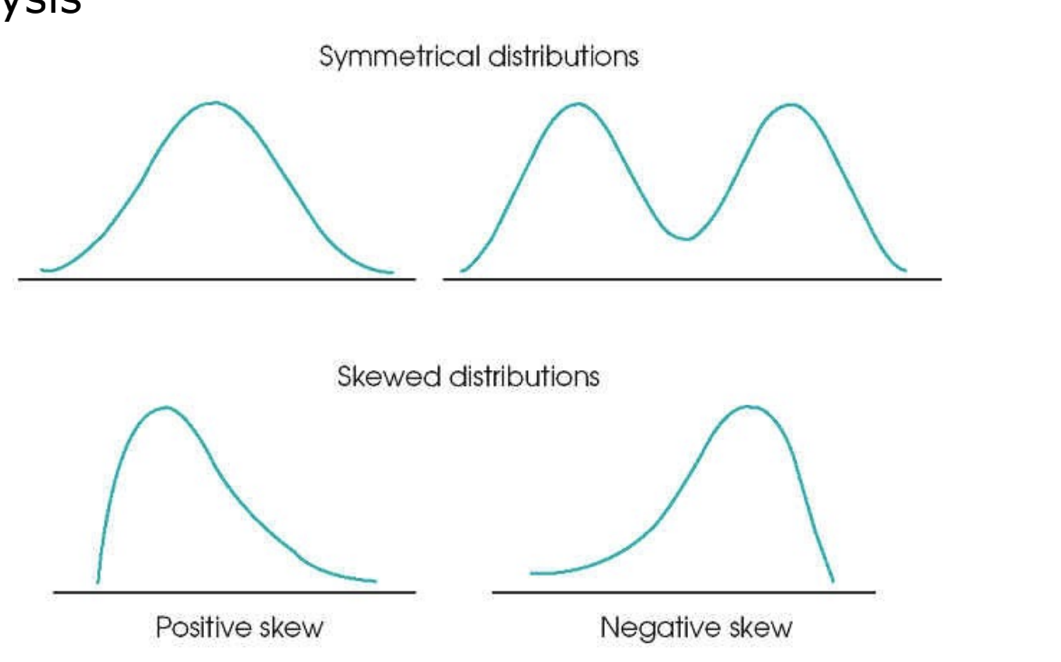
useful to look at your data before beginning analysis

measures of variability

• range

  • interval between lowest and highest values

  • influenced by outliers

  • rough measure of spread

• interquartile range

  • also known as mid-spread or middle 50%

  • defined as the interval between the data score at the 25th and 75th percentile

  • gives an impression of the dispersion of the data

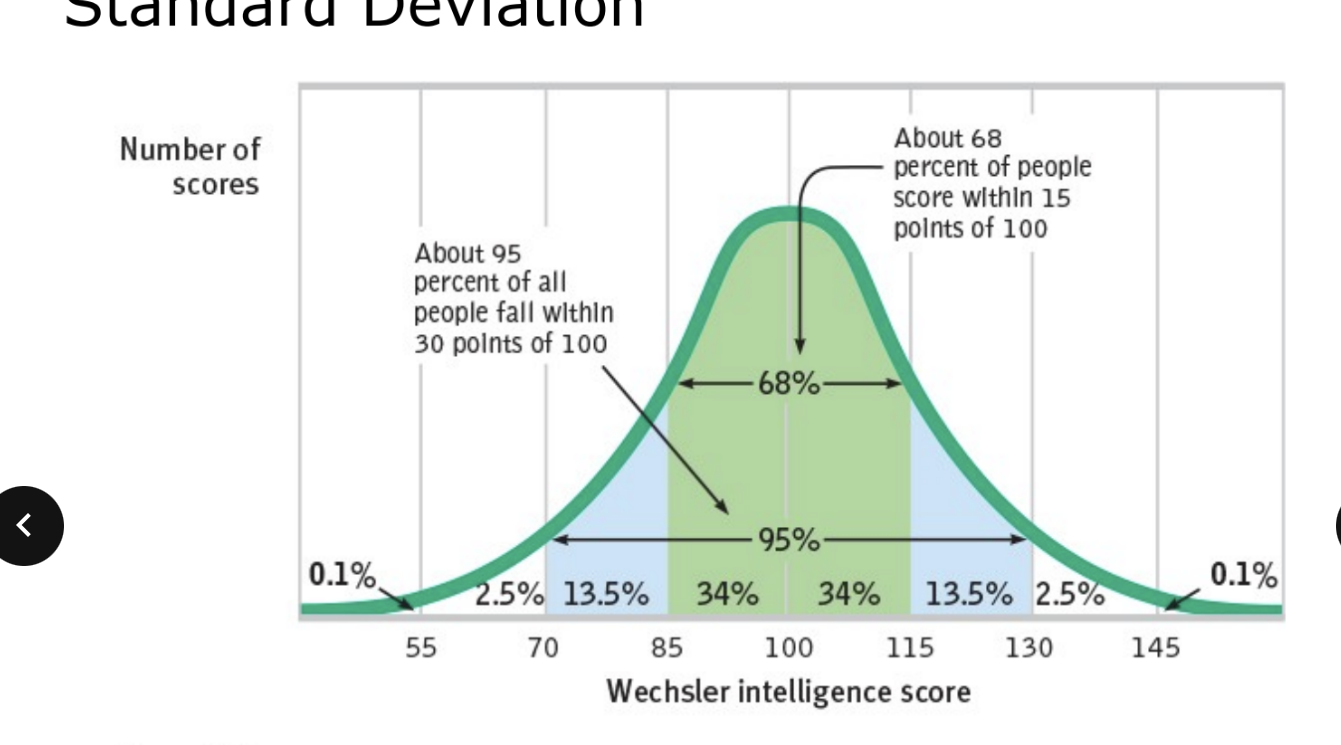
• standard deviation (SD)

  • an index of variability of study data around the mean of the data

  • only useful when data are normally or near normally distributed

  • only applicable to interval or ratio data

    • +/- 1 SD includes 68% of samples

    • +/- 2 SD includes 95% of samples

    • +/- 3 SD includes >99% of samples

  • the smaller the standard deviation the less variability in the data

• standard error of the mean

• confidence interval

measures of variability: standard error of the mean (SEM)

• estimates the precision or relaibility of a sample as it relates to the population; estimates the true mean of the population from which the samplke was derived

• the true mean of the population will fall within ± 2 SEM, 95% of the time

• useful for calculating the confidence interval (on exam)

measures of variability: standard deviation vs standard error of the mean

• both are measures of variability

• SD describes the variability within the sample; SEM represents the variability of the mean itself

• SEM will always be SMALLER than the SD (on exam)

measures of variability: confidence intervals (CI)

• method of estimating the range of values likely to include the true value of the population parameter

• gives us a measure of confidence of the sample statistic would be representative of the true population parameter

• the width of the CI depends on on the SEM and the degree of confidence chosen (95% if most common)

• the 95% CI = range of values broad enough that, if the entire population could be studied, 95% of the time the population mean would fall within the CI calculated from the sample

• can help evaluate the clinical relevance of results

• on exam know how to interpret confidence values

95% CI

• a range of values that are likely to cover the true parameter

• with a 95% CI, you assume that 95% of random samples taken will contain the true mean

• we can never be certain if your interval covers the true mean or not

why do we test hypotheses?

• main concern of study is to compare results from treatment vs placebo groups

• statistics generates probabilities (p-values) that the data aligns with assumptions

• easiest logical starting point for comparison to assume no difference between/w groups (null hypothesis)

• if the data does NOT confirm to this assumption → reject null hypothesis for alternative hypothesis

statistical inferences (superiority testing)

null hypothesis (Ho)

• there is NO difference between groups

alternative hypothesis (Ha)

• a true difference exists between groups

• NO statistical test rejects or fails to reject the null with absolute certainity; test only allows an estimation of the probability that a correct decision is being made in rejecting or NOT rejecting null

hypothesis examples

an RCT tests if a new drug reduces asthma exacerbations compared to ICS inhalers (on exam)

• Ho = NO difference in exacerbations between groups

• Ha = a difference exists between groups

are current smokers at a higher risk of COPD than former smokers?

• Ho = the risk of COPD is the same between former and current smokers

• Ha = the risk of COPD is different between former and current smokers

types of error regarding null hypothesis

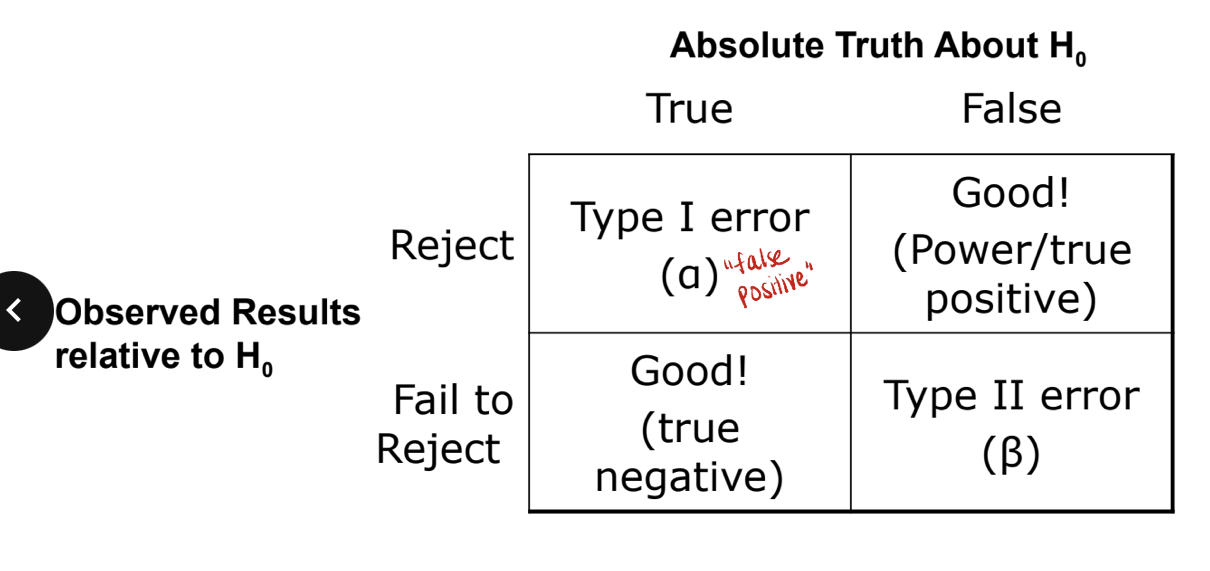
example of type I vs type II error

type I error = false positive

• this is when the null hypothesis is true which means there is NO difference between groups but you reject this and say there IS a difference

type II error = false negative

• this is when the null hypothesis is false which means there IS a difference between groups but you fail to reject it (accept it as true) and say there is NO difference

type I error (alpha error)

• worst error

• reject the null hypothesis when, in fact, the null hypothesis is true and should NOT be rejected

  • i.e. investigator concludes that there IS a difference between drug A and B when in fact there is NO difference

• the probability of making a type I is represented by alpha

• probaability of false-positive results

• usually due to random chance, improper sampling technique, confounding

type II error (beta error)

• fail to reject the null hypothesis when it is false

  • i.e. the investigator concludes that there is NO difference between drug A and B when there IS a difference

• type II error closesly related to concept of power

• probability of false-negative results

• usually due to saple size being too small

P values

• simplest terms → how likely your data are to occur due to random chance under the assumption that the null hypothesis is true

• represents the probability that a type I error has been commited (erroneous rejection of a true Ho)

• part of the overall evaluation of the study

• one-tailed vs two-tailed tests

  • one tailed → only see a difference in one direction

  • two tailed → concerned with ANY difference (either direction)

  • the authors should always state if the test is one-tailed or two-tailed

P-value: mathematical example

• low P value → reject null hypothesis

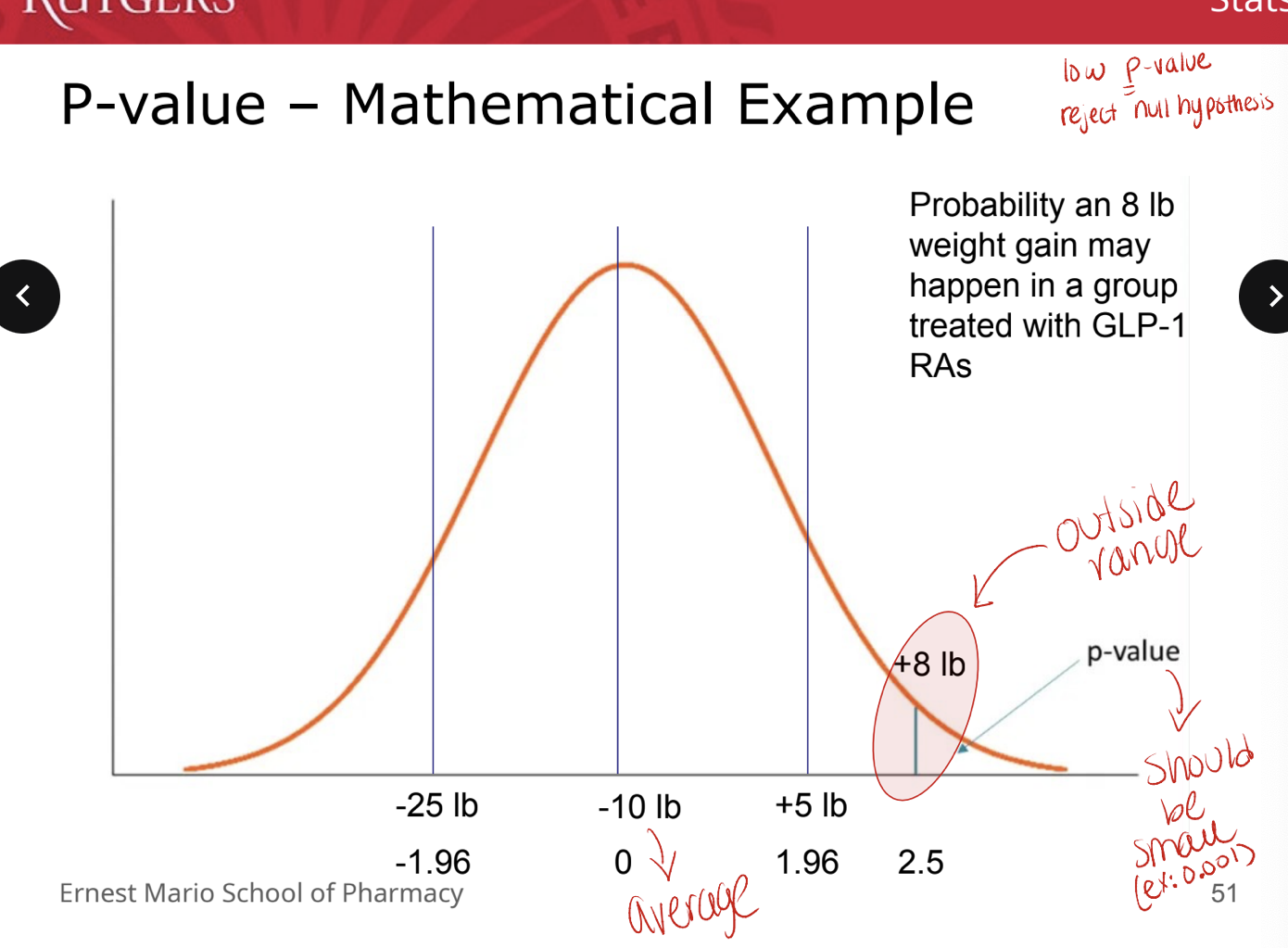
alpha and P-values

• how do we decide what p-value will be considered significant?

• at what p-value do we decide that there is a good enough chance that our results were NOT due to random chance?

• alpha is selected BEFORE data analysis (on exam)

  • represents threshold for p-value significance

  • alpha = 0.05 = routine

power

• related to (prespecified) beta

  • probability of a type II error or accepting the null hypothesis which was in fact, false

• power = probability that a staistical test will detect a deviation from the null hypothesis

• 80% is regarded as an acceptable power value 

  • represents a 20% probability that a type II error has been committed

• magnitude depends on

  • amount of difference the treatment causes and # of events in control subjects

  • alpha

  • sample size

know why these values matter

delta

• based upon previous studies

  • the minimum clinically important difference (MCID) the authors are seeking

• statistical significance does NOT inherently mean clinical significance 

  • consider a study that shows a difference in avg SBP of 1 mmHg with a p<0.001

• for many outcomes, the FDA has specified levels of clinical significance 

  • changes in blood psi, HbA1c, etc. 

• difference in groups you are studying → see if value matches expected value

sample size (N)

• # of patients required in the study

• based on 4 factors

  • alpha or level of significance (i.e. probability of false positive) → never changes

  • beta (smaller beta, higher power → larger sample size)

  • delta (i.e. amount of difference to be detected) (smaller difference → larger sample size)

  • standard deviation (i.e. variation) (smaller variation → smaller sample size)

example: waterfall study

the anticipated incidence of moderately severe or severe acute pancreatitis was 35%. we calculated that a sample size of 744 (N) with 372 pts in each group would provide the trial with 80% power (power) to detect a between-group difference of 10 percentage points (delta) (between 35% and 25%) at a two-sided significance level (alpha) of 0.05 (alpha) with an antipcated withdrawal of 10% of the patinets)

95% confidence interval

for absolute differences: 

• if the CI does NOT cross 0 → statistically significant

• if the confidence interval crosses 0 → NOT statistically significant

• clinical relevant interpreted from how close CI comes to zero