Discrete Mathematics Chapter 1 - The Foundations: Logic and Proofs
0.0(0)
0.0(0)
Card Sorting
1/15
Earn XP
Study Analytics
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No study sessions yet.
16 Terms
1
New cards
What is a proposition?
A proposition is a declarative statement, which is either true or false.
2
New cards
Which of these are propositions, which are not? Why?
1 + 1 = 2
1 + 1 = 3
x + 2 = 3
1 + 1 = 2
1 + 1 = 3
x + 2 = 3
1 + 1 = 2 and 1 + 1 = 3 are both propositions, the first one being true and the other being false.
x + 2 = 3 is not a proposition. That is because we cannot determine whether or not the statement is true/false, since we do not know the value of x.
x + 2 = 3 is not a proposition. That is because we cannot determine whether or not the statement is true/false, since we do not know the value of x.
3
New cards
What is logical operators?
Logical operators combine propositional variables to form new compound propositions.
4
New cards
What are the logical operators in discrete math?
1. Negation or “Not” → ¬p
True when p is False and False when p is True
2. Conjunction or “AND” → p ^ q
True if both p and q are True, False otherwise
3. Disjunction or “OR”, → p v q
True if at least any of the propositional variables p or q is True.
4. Exclusive OR or “XOR” → p **⊕** q
If both propositional variables p and q are True, then the proposition is False. True if and only if its arguments differ
5. Conditional Statement “if then”, p → q
“If p, then q”. False when p is True and q is False, otherwise True.
6. Biconditional Statement “if and only if”. p ↔ q
True if p and q are the same (both are True or both False)
5
New cards
Logical Equivalence
Two compound propositions are **logically equivalent** if they have the same truth value for all possible values of their propositional variables.
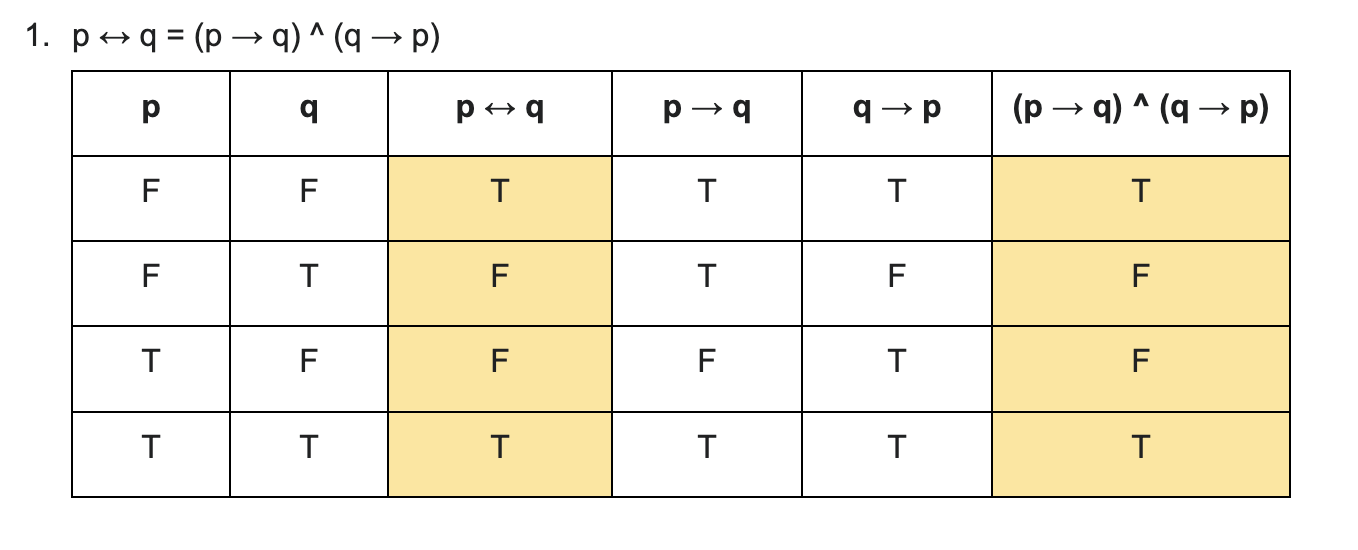
6
New cards
What is the precedence of logical operators?
1. ¬ (NOT)
2. ^ (AND)
3. v (OR)
4. → (COND)
5. **↔** (BICOND)
\
If should be interpreted as first applying the NOT to p, then taking the result of this operation AND q.
¬ p ^ q = (¬ p) ^ q
\n
AND has higher priority than OR, in this case we would write it as:
p v q ^ r = p v (q ^ r)
\n
Here, OR has higher priority than the conditional.
p → q v r = p → (q v r)
7
New cards
Tautology
A compound proposition which is always True
8
New cards
Contradiction
A compound proposition which is always False
9
New cards
Contingency
A compound proposition which is both True and False for the propositional variables
10
New cards
De Morgans Laws
1. ¬(p ^ q) = ¬p v ¬q
2. ¬(p v q) = ¬p ^ ¬q
11
New cards
Identity Laws
p ^ T = p
p v F = p
p v F = p
12
New cards
Domination Laws
p ^ F = F
p v T = T
p v T = T
13
New cards
Idempotent Laws
p ^ p = p
p v p = p
p v p = p
14
New cards
Double negation
¬(¬p) = p
15
New cards
Commutative Laws
p v q = q v p
p ^ q = q ^ p
p ^ q = q ^ p
16
New cards
Association Laws
(p ^ q) ^ r = p ^ (q ^ r) = p ^ q ^ r
(p v q) v r = p v (q v r) = p v q v r
(p v q) v r = p v (q v r) = p v q v r