egzamin ze statystyki i matematyki
5.0(2)Studied by 6 people
Card Sorting
1/100
Earn XP
Description and Tags
Last updated 2:49 PM on 1/27/23
Name | Mastery | Learn | Test | Matching | Spaced | Call with Kai |
|---|
No analytics yet
Send a link to your students to track their progress
101 Terms
1
New cards
ciąg liczbowy rzeczywisty
funkcja określona na zbiorze liczb **naturalnych** o wartościach w zbiorze liczb **rzeczywistych**
2
New cards
ciąg arytmetyczny
ciąg dla którego **różnica** kolejnych dwóch wyrazów jest stała
3
New cards
ciąg geometryczny
ciąg dla którego **iloraz** dwóch kolejnych wyrazów jest stały
4
New cards
symbole nieoznaczone
zdjecie
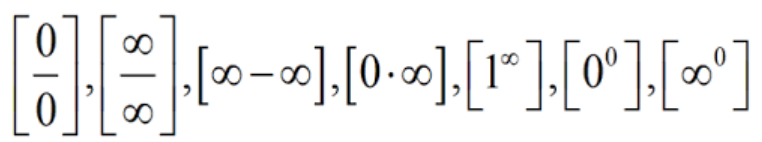
5
New cards
własności ciągu z liczbą e
ogarniczony, rosnący, zbieżny
6
New cards
co to znaczy że ciąg jest zbieżny
ma granicę
7
New cards
twierdzenie o trzech ciągach
jeśli an≤bn≤cn oraz an i cn mają równe granice to ciąg bn też będzie miał taką samą granice
8
New cards
warunek konieczny zbieżności szeregu
wyraz ogólny dąży do 0 lim a=0
9
New cards
Kryterium d’Alemberta
zdjęcie

10
New cards
kryterium Cauchy’ego
zdjęcie

11
New cards
kryterium Leibniza
zdjęcie

12
New cards
kryterium porównawcze
zdjęcie

13
New cards
różniczkowanie
odnajdywanie pochodnej funkcji
14
New cards
pochodna funkcji w punkcie x0
granica ilorazu różnicowego tej funkcji w punkcie x0 gdy przyrost delta x dąży do 0
15
New cards
wzór na pochodną funkcji w punkcie x0
zdjęcie
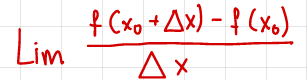
16
New cards
interpretacja geometryczna pochodnej funkcji
* pochodna funkcji x0 = tangens kąta nachylenia stycznej do wykresu funkcji f w punkcie x0
* pochodna funkcji f(x) = współczynnik kierunkowy prostej stycznej do wykresu w punkcie x0
* pochodna funkcji f(x) = współczynnik kierunkowy prostej stycznej do wykresu w punkcie x0
17
New cards
całkowanie
działanie odwrotne do różnicznkowania
18
New cards
pochodna funkcji stałej
y’=(12)’=0
19
New cards
y’=(x)’=
x
20
New cards
interpretacja geometryczna całki oznaczonej
trapez krzywoliniowy, pole obszaru ograniczonego łukiem krzywej funkcji oraz prostymi x=a i x=b (granice) równa się całce oznaczonej tej funkcji
21
New cards
własności całki oznaczonej
* po przestawieniu granic całka zmienia znak na przeciwny
* całka o tej samej dolnej i górnej granicy =0
* przedział w którym obliczamy całkę wolno dzielić na części
* całka o tej samej dolnej i górnej granicy =0
* przedział w którym obliczamy całkę wolno dzielić na części
22
New cards
liczba zespolona
uporządkowana para liczb rzeczywistych z=(x,y)
23
New cards
Płaszczyzna zespolona
zbiór wszystkich liczb zespolonych
24
New cards
suma liczb zespolonych z=(a,b) w=(c,d)
z+w=(a+c,b+d)
25
New cards
iloczyn liczb zespolonych
z\*w=(ac-bd,ad+bc)
26
New cards
element neutralny dodawania
z=(0,0)
27
New cards
element przeciwny do liczby z=(a,b)
\-z=(-a,-b)
28
New cards
element neutralny mnożenia
z=(1,0)
29
New cards
element odwrotny liczby z
zdjęcie
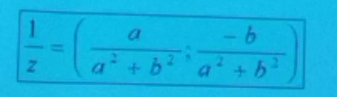
30
New cards
jednostka urojona
liczba zespolona (0,1)
31
New cards
warunek jednostki urojonej
i^2=-1
32
New cards
postać algebraiczna liczby zespolonej
z=x+iy/z=a+ib
33
New cards
liczba sprzężona do liczby zespolonej
obraz liczby zespolonej w symetrii do osi Re z (z=x-iy)
34
New cards
moduł liczby zespolonej
odległość punktu (x,y) od początku układu współrzędnych
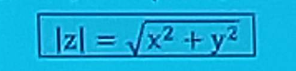
35
New cards
część rzeczywista liczby zespolonej (it realis)
liczba x (Re z=x)
36
New cards
część urojona liczby zespolonej (it imaginalis)
liczba y (Im z=y)
37
New cards
macierz kwadratowa
liczba wierszy = liczba kolumn
38
New cards
macierz zerowa
wszystkie elementy macierzy są równe 0
39
New cards
wyznacznik macierzy kwadratowej
takie odwzorowanie które danej macierzy przyporządkowuje dokładnie jedną liczbę rzeczywistą detA
40
New cards
reguła Sarrusa
służy do obliczania współczynnika macierzy 3x3
41
New cards
właściwości wyznaczników
* przestawienie dowolnych wierszy (lub kolumn) zmienia wartość współczynnika na przeciwną
* przestawienie wszystkich wierszy na miejsce jego kolumn i odwrotnie bez zmiany ich porządku nie zmienia wartości współczynnika
* jeśli wyznacznik ma dwa wiersze lub kolumny identyczne to jego wartość równa się zeru
* jeśli wyznacznik ma jakiś wiersz lub kolumnę złożoną z samych 0 to jego wartość równa się 0
* jeśli wszystkie elementy dowolnego wiersza lub kolumny wyznacznika pomnożymy przez pewną liczbę to wyznacznik też zostaje pomnożony przez tą liczbę
* jeśli do elementów dowolnego wiersza lub kolumny dodamy lub odejmiemy element innego wiersza lub elementy innego wiersza pomnożone przez tę liczbę to wartość wyznacznika nie zmieni się
* przestawienie wszystkich wierszy na miejsce jego kolumn i odwrotnie bez zmiany ich porządku nie zmienia wartości współczynnika
* jeśli wyznacznik ma dwa wiersze lub kolumny identyczne to jego wartość równa się zeru
* jeśli wyznacznik ma jakiś wiersz lub kolumnę złożoną z samych 0 to jego wartość równa się 0
* jeśli wszystkie elementy dowolnego wiersza lub kolumny wyznacznika pomnożymy przez pewną liczbę to wyznacznik też zostaje pomnożony przez tą liczbę
* jeśli do elementów dowolnego wiersza lub kolumny dodamy lub odejmiemy element innego wiersza lub elementy innego wiersza pomnożone przez tę liczbę to wartość wyznacznika nie zmieni się
42
New cards
skala nominalna
NAJPROSTSZA, pozwala określić przynależność elementów danego zbioru (np populacji ludzi) do wyróżnionych dla danej cechy (np kolor oczu) kategorii jakościowych (np u brunetów)
43
New cards
skala nominalna dychotomiczna (dwupunktowa, dwudzielna)
wszystkie elementy danego zbioru są podzielne na dwie grupy rozłączne, czyli takie które nie posiadają elementów wspólnych (np płeć)
44
New cards
skala porządkowa
podczas rangowania poszczególnych wyników pomiarów przypisujemy im kolejny numer porządkowy czyli tzw rangę, utworzone rangi są wykorzystywane w dalszych przeliczeniach statystycznych
45
New cards
skala interwałowa (przedziałowa)
stosuje się ją wówczas, gdy zbiór wyników zawiera się w zbiorze liczb rzeczywistych, wynikom wyrażonym w tej skali można przypisać określoną wartość mierzoną w ściśle zidentyfikowanych jednostkach (np pomiary masy, długości, temperatury)
46
New cards
dokładność pomiaru
różnica między najmniejszym a największym pomiarem musi mieścić się w zakresie od 30 do 300 jednostek pomiarowych
47
New cards
od czego zależy dokładność pomiarów
możliwości aparatury, celu badań i zasad przestrzeganych w danej dyscyplinie naukowej
48
New cards
granice praktyczne
np 210-229,9
49
New cards
granice rzeczywiste
np 209,95-229,95
50
New cards
średnia arytmetyczna ważona
stosuje się ją gdy elementom danego zbioru chcemy przypisać większą wagę, aby miały one większy wpływ na obliczaną wartość średniej arytmetycznej
51
New cards
średnia geometryczna
stosowana jest gdy wyniki zmieniają się w przybliżeniu w postępie geometrycznym tzn. gdy kolejna wielkość w szeregu powstaje przez pomnożenie przez stały mnożnik wielkości bezpośrednio ją poprzedzającej, można nią obliczyć średnie tempo przyrostu badanej cechy (np tempo przyrostu masy ciała) (tylko liczby dodatnie)
52
New cards
średnia harmoniczna
służy najczęściej do obliczania tzw. efektywnej wielkości populacji, kształtu, dominacji czy zagęszczenia. Stosuje się ją również wtedy, gdy chcemy obliczyć średnią wartość badanej cechy, a zbiór wyników zawiera wartości różniące się od siebie o kilka rzędów wielkości
53
New cards
współczynnik zmienności
umożliwia porównanie zmienności wyników pomiarów, które nie zostały wyrażone w tych samych jednostkach lub pobrano je z różnych źródeł
54
New cards
kodowanie
polega na dodawaniu, odejmowaniu, mnożeniu i dzieleniu wszystkich wyników przez wartość stałą w celu uproszczenia obliczeń i graficznego przedstawienia wyników badań
55
New cards
transformacja
polega na pierwiastkowaniu, potęgowaniu czy logarytmowaniu danych pomiarowych, można też użyć funkcji trygonometrycznych
56
New cards
kombinacje
pozwalają policzbyć na ile sposobów można wybrać k elementów z n-elementowego zbioru (nie wybieramy wszystkiego, kolejność nie jest istotna)
57
New cards
permutacje
np ilość kombinacji w które można ułożyć 5 osób w kolejkę (bez powtórzeń) (5!=) (wszystkie elementy)
58
New cards
wariacja
nie musimy używać wszystkich elementów, z powtórzeniami i bez powtórzeń
59
New cards
wariancja
średnia arytmetyczna kwadratów odchyleń poszczególnych wartości cechy jednostek zbiorowości od ich średniej, kwadrat odchylenia standardowego
60
New cards
klasyczna definicja prawdopodobieństwa
stosunek zdarzeń elementarnych sprzyjających zdarzeniu, do wszystkich zdarzeń elementarnych, jednakowo możliwych i wykluczających się wzajemnie
61
New cards
własności prawdopodobieństwa
* prawdopodobieństwo zdarzenia niemożliwego wynosi 0
* jeśli zdarzenie A pociąga za sobą zdarzenia B to P(A) ≤ P(B)
* dla każdego zdarzenia A zawartego w omega zachodzi P(A) ≤ 1
* jeśli zdarzenie A pociąga za sobą zdarzenie B, to prawdopodobieństwo różnicy zdarzeń jest równe różnicy prawdopodobieństw tych zdarzeń
* prawdopodobieństwo zdarzenia przeciwnego do zdarzenia A wynosi P(A’) = 1 - P(A)
* jeśli zdarzenie A pociąga za sobą zdarzenia B to P(A) ≤ P(B)
* dla każdego zdarzenia A zawartego w omega zachodzi P(A) ≤ 1
* jeśli zdarzenie A pociąga za sobą zdarzenie B, to prawdopodobieństwo różnicy zdarzeń jest równe różnicy prawdopodobieństw tych zdarzeń
* prawdopodobieństwo zdarzenia przeciwnego do zdarzenia A wynosi P(A’) = 1 - P(A)
62
New cards
zmienna losowa
każda funkcja na zbiorze omega i przybierająca wartości w zbiorze liczb rzeczywistych
63
New cards
zmienna losowa skokowa
zbiór wartości które może przyjmować zmienna jest skończony
64
New cards
zmienna losowa ciągła
zbiór wartości które może przyjmować zmienna jest niepoliczalny
65
New cards
rozkład zero-jedynkowy
przeprowadza się jedno doświadczenie losowe (n=1), możliwe są tylko dwa wyniki - sukces (1) lub porażka (0)
66
New cards
rozkład dwumianowy
więcej niż jedno zdarzenie losowe (n>1), możliwe są tylko wyniki p i q
67
New cards
prawdopodobieństwo alternatywy
zdarzenie losowe, które zachodzi wtedy gdy zachodzi przynajmniej jedno ze zdarzeń je tworzących (albo) (równe sumie prawdopodobieństw tych zdarzeń)
68
New cards
prawdopodobieństwo koniunkcji
zdarzenie losowe polegające na tym, że kilka zdarzeń losowych zaszło równocześnie (i) (równe iloczynowi prawdopodobieństw tych zdarzeń)
69
New cards
rozkład prawoskośny
p
70
New cards
rozkład lewoskośny
p>0,5
71
New cards
rozkład normalny
rozkład ciągły i symetryczny którego postać zależy od dwóch parametrów mi i sigma (μ,σ)
72
New cards
gęstość prawdopodobieństwa
średnia ilość prawdopodobieństwa przypadająca na jednostkę długości przedziału gdy długość przedziału dąży do 0
73
New cards
rozkład platykurtyczny
jeśli rozkład wyników pomiarów mocno odbiega od wartości średniej to sigma przyjmuje wysokie wartości i rozkład normalny ma wtedy kształt rozpłaszczony
74
New cards
rozkład leptokurtyczny
jeśli rozkład wyników nie odbiega mocno od wartości średniej to sigma przyjmuje niskie wartości i rozkład normalny ma szpiczasty kształt
75
New cards
rozkład normalny standaryzowany
ma zdefiniowaną średnią arytmetyczną mi=0 i zdefiniowane odchylenie standardowe sigma=1
76
New cards
ile wynosi pole pod krzywą gęstości prawdopodobieństwa
1
77
New cards
na co wskazuje jednostka z
jednostka standaryzowana, wskazuje o ile odchyleń standardowych pojedynczy wynik jest oddalony od średniej
78
New cards
hipoteza badawcza
przypuszczenie dotyczące badanego zjawiska czy rozważanego problemu
79
New cards
hipoteza statystyczna
przypuszczenie dotyczące badanych danych
80
New cards
hipoteza zero
brak istotnych różnic w wynikach, przyjmujemy kiedy wartość statystyki testu będzie mniejsza niż wartość krytyczna
81
New cards
hipoteza alternatywna (1)
istotne różnice w wynikach, przyjmujemy kiedy wartość statystyki testu będzie większa od wartości krytycznej
82
New cards
poziom istotności
prawdopodobieństwo uzyskania z testu statystycznego wartości, która nakazuje nam odrzucenie hipotezy zerowej na rzecz hipotezy alternatywnej, mimo, że hipoteza zerowa może być prawdziwa (określa prawdopodobieństwa popełnienia błędu pierwszego rodzaju)
83
New cards
błąd pierwszego rodzaju
odrzucamy prawdziwą hipotezę zerową i przyjmujemy fałszywą hipotezę alternatywną
84
New cards
błąd drugiego rodzaju
odrzucamy prawdziwą hipotezę alternatywną i przyjmujemy fałszywą zerową
85
New cards
który test jest silniejszy (konserwatywny/liberalny)
konserwatywny
86
New cards
estymacja parametrów
wyznaczenie takiego przedziału liczbowego który z nadanym z góry prawdopodobieństwem (1-alfa) zwanym współczynnikiem ufności poryje nieznaną wartość szacowanego parametru populacji
87
New cards
współczynnik ufności
zależy od przyjętego poziomu istotności, jeśli alfa=0,05 to współczynnik ufności =0,95
88
New cards
test Q-dixona
umożliwia wyeliminowanie tzw. błędów grubych czyli błędów pomiarowych które różnią się od pozostałych (błąd pomiarowy, odczytu)
89
New cards
test t-studenta
stosujemy go w celu wykazania istotnych różnic między dwiema grupami
90
New cards
test F
sprawdza jednorodność wariancji, trzeba go zrobić przed zastosowaniem testu t dla prób niezależnych
91
New cards
założenie analizy wariancji
obowiązuje we wszystkich rodzajach ANOVA i wymaga aby pomiar zmiennej zależnej miał rozkład normalny w obrębie każdej wyróżnionej grupie danych i wariancja pomiarów była jednakowa we wszystkich grupach (i pobieranie losowe)
92
New cards
test u
mocniejszy od testu serii, bardziej precyzyjnie od niego sprawdza różnice w rozkładzie liczb między dwiema grupami
93
New cards
test Kniskala-Wallisa
nieparametryczna alternatywa klasyfikacji prostej, stosuje się przy naruszeniu założeń ANOVA
94
New cards
test Wilcoxona
nieparametryczna alternatywa testu t-studenta dla przypadku dwóch równolicznych prób dających się połączyć w pary
95
New cards
test ANOVA
pomiary muszą być w rozkładzie normalnym oraz wariancja pomiarów musi być jednakowa we wszystkich grupach
96
New cards
test chi-kwadrat
sprawdza hipotezę, jest to każdy test statystyczny w którym statystyka testowa ma rozkład chi kwadrat (wartość oczekiwana nie może być mniejsza niż 5)
97
New cards
model regresji
opisuje zależność między dwoma zmiennymi, z których jedna (Y) jest zmienną losową o rozkładzie normalnym, druga natomiast (X) jest zmienną nielosową
98
New cards
model korelacji
współzależność dwóch zmiennych, z których obie Y i X są zmiennymi losowymi
99
New cards
wartość krytyczna
wyznacza obszar w którym gęstość prawdopodobieństwa przyjmuje wartości niższe od założonego poziomu istotności
100
New cards
współczynniki korelacji
od -1 do +1