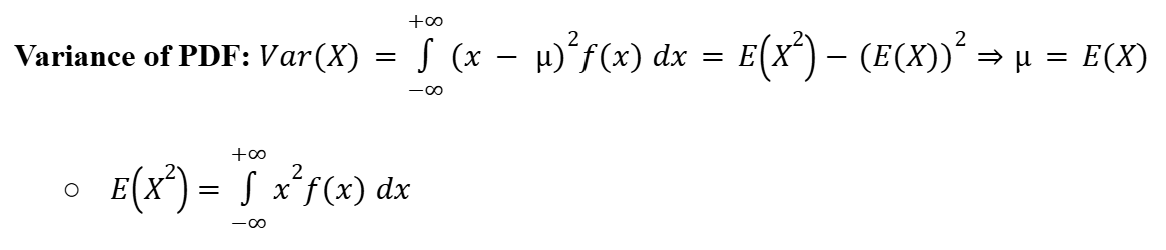UNIT 4.2. Probability

Formulae (SL & HL)

Probability

• Probability: Measure of the likelihood of an event to occur.

  • Probability is always less than or equal to 1, the probability of an impossible event is 0, and the probability of a guaranteed event is 1.

Sample Space: A sample space contains all possible outcomes.

Probability of an event ‘A’

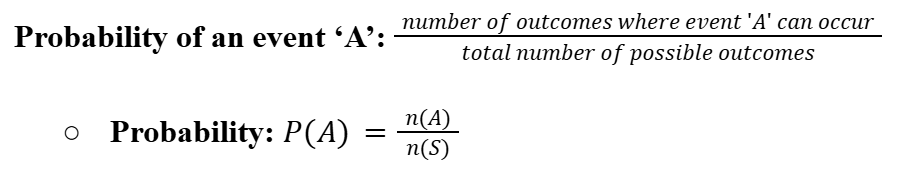
Complementary Factor (Probability)

Independent Events

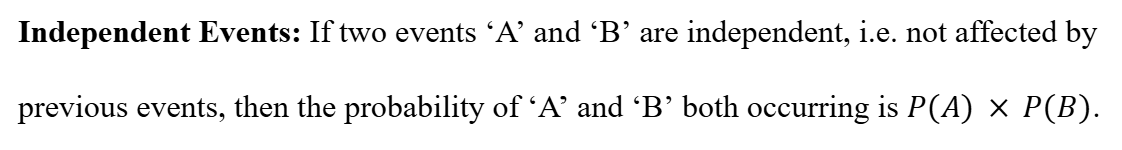
Two-Way Table (Probability)

A two-way table is a tabular list of all possible outcomes of any event.

Probability Tree

A probability tree is a representation of the sample space when multiple events occur and branch out. The final probability at the end of each branch is the multiple of all the probabilities corresponding to that branch.

Dependent Events

For dependent events, where the probability of the event occurring is based on past events, the probability will change based on the outcome of the previous event.

Venn Diagram

A Venn Diagram represents the similarities and differences between two or more sample spaces.

Union (Probability)

All the terms in both sets.

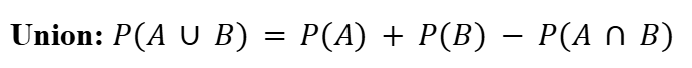
Intersection (Probability)

All the common terms in both sets.

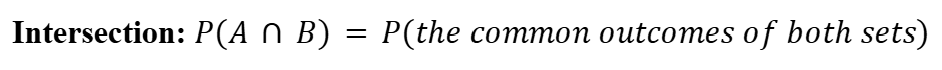
First Axiom of Probability

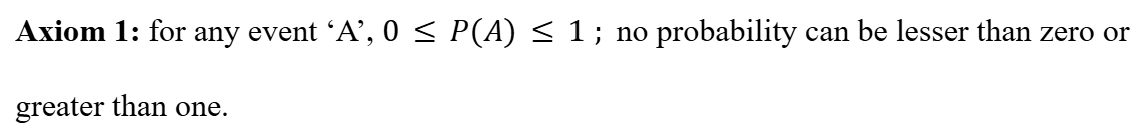
Second Axiom of Probability

For a sample space ‘S’, P(S) = 1 i.e. the probability of all occurrences is one.

Third Axiom of Probability

In probability, two events are mutually exclusive if only one event can occur at a given time in a particular experiment.

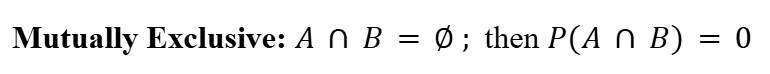
Fourth Axiom of Probability

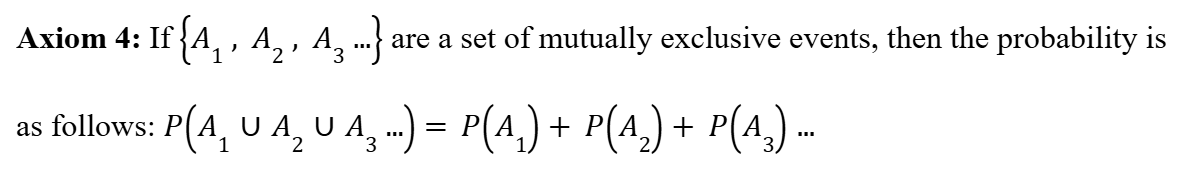
Direct Random Variable

A random variable is a quantity whose value depends on the outcome of a probability experiment. Random variables are represented using capital letters.

Example of Direct Random Variables

If ‘X’ represents the number of sixes obtained when a dice is rolled three times, then the probability is P(X=x) where ‘x’ is the outcome of the experiment, in this case, either 0, 1, 2, or 3.

Properties of Random Variables

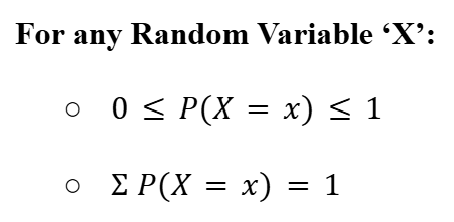
Expected Value (Direct Random Variables)

Binomial Distribution

Expectation (Binomial Distribution)

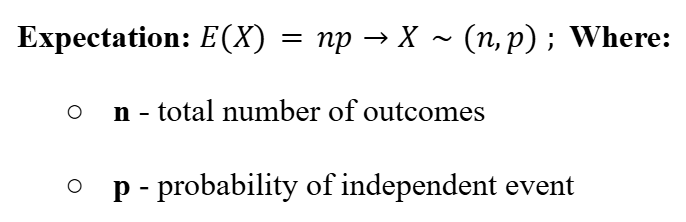
Variance (Binomial Distribution)

Normal Distribution

• Normal Distribution: A normal distribution follows a “bell-shaped” curve, with most values grouped around a central value.

  • Perfect Normal Distribution: Perfectly symmetrical around the mean. The mean, median, and mode are then all the same.

Formula for Normal Distribution (Not Needed)

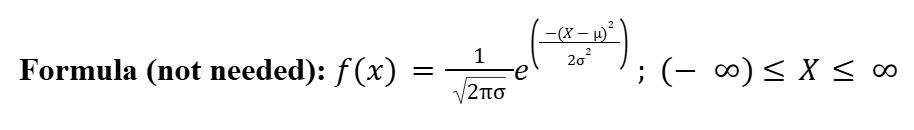
Standard Normal Distribution

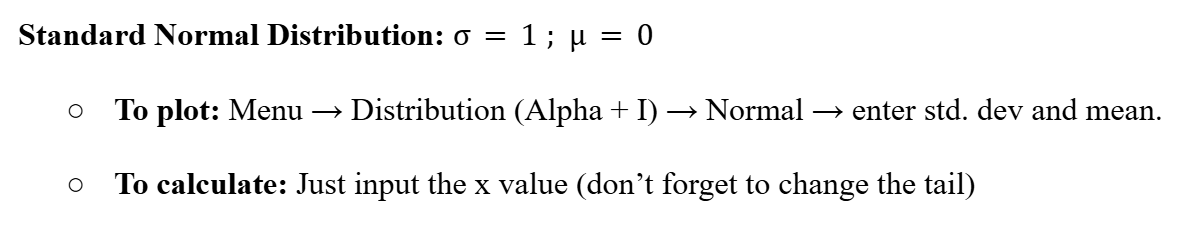
Standardization (Normal Distribution)

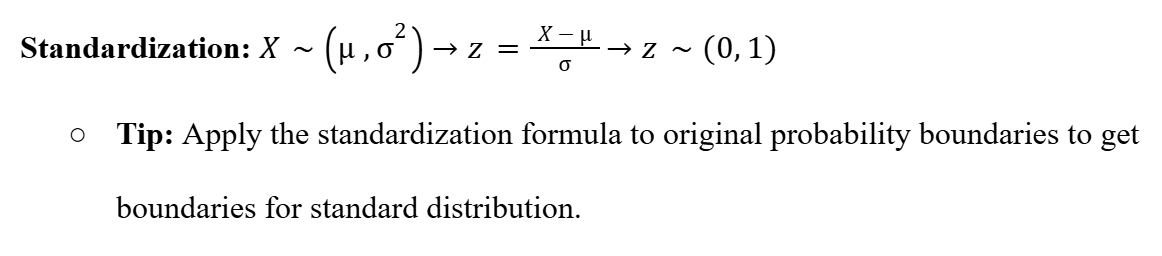
Inverse Normal Distribution

To find the inverse, a.k.a. the ‘X’ value, simply create the normal distribution with the given mean and standard deviation, move over to the probability, and enter the given probability to find X based on your boundaries.

Tricks for Inverse Normal Distribution

Probability Density Function (PDF)

Probability from a Probability Density Function (PDF)

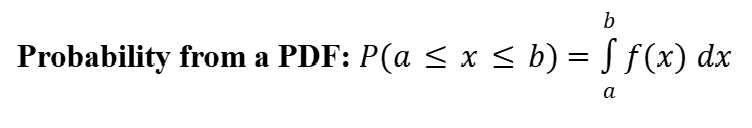
Mode (Probability Density Function)

Arithmetic Mean (Probability Density Function)

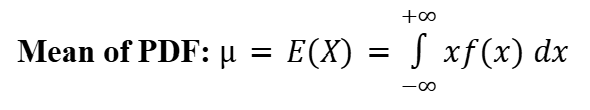
Median (Probability Density Function)

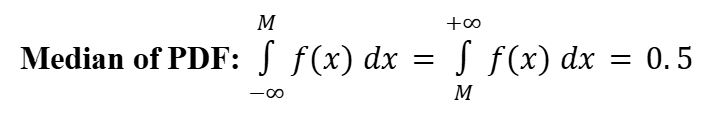
Variance (Probability Density Function)