Money, Prices and Inflation: Nominal values in the long run

What is money?

Money is what money does. It is:

• A medium of exchange

• unit of account

• store of value

These functions of money determine what assets are money. A narrow definition of money (M1) based on it being a medium of exchange is currency. This is referred to as MONETARY BASE.

Bank deposits which can be used to make transactions (eg using debit cards) is also a form of money.

Financial instruments like credit cards are NOT money but they do increase the ability of money to make transactions and hence influence the demand for narrow money (velocity of money).

Historical definitions of money

NARROW MONEY is something that individuals will accept in payment for goods and services and move a society from a barter to monetary economy.

Initially money developed as commodity money.

Money can also be created from social conventions like the use of claims on stone wheels and the island of Yap.

The development and acceptance of fiat money enhanced the capability of the monetary economy since it did not constrain monetary creation to precious metal supply and removed the large cost involved with commodity money.

What are the operational definitions of money?

Money is relatively easy to define in a narrow sense where the medium of exchange function is crucial.

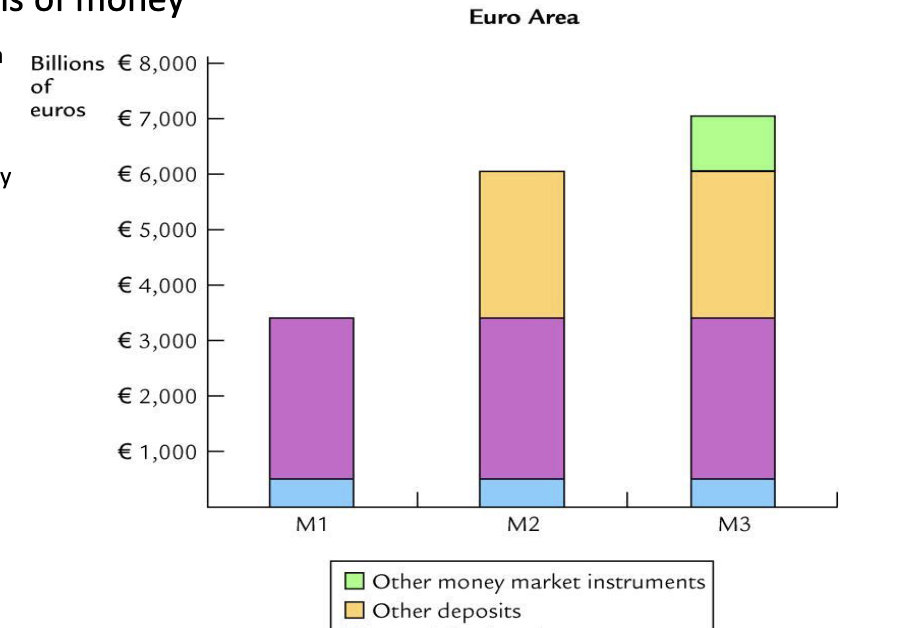
Many central banks monitor multiple money definitions such as:

• M0 - Monetary base

• M1 - Money as means of payment

• M2 - (M1 plus non-transactions deposits which can be rapidly converted into money)

• M3 - Including high liquid stores of value such as Money Market funds

Bank of England also monitor M4, a very broad money supply.

Banks and the money supply

Banks determine how much money exists.

We start with the narrow definition of money supply (M) as the sum of household demand for currency (CH)) and demand deposits (D).

M = CH+D

To understand how D is determined, we must introduce the FRACTIONAL RESERVE BANKING concept.

What is fractional reserve banking?

Suppose that banks operate under 100% reserve banking.

This means that when a bank receives deposits it will hold all of these deposits as reserves. We can look at development of fractional reserve banking. In this situation banks hold only a fraction of their deposits as reserves and then lend out the rest.

Suppose the bank starts with an inflow of deposits φ

The bank also retains a fraction k of its deposits as a cash reserve to meet sudden liquidity needs in case deposits are withdrawn unexpectedly

So for an initial inflow of deposits φ the bank can make lending by creating deposits equal to (1-k)φ

What happens to the deposits (1-k)φ?

This lending comes into the bank as further deposits and the bank then lends on (1-k) of that increase. The second round of lending generates (1-κ)²Φ lending for the third round and so on.

The process continues for n lending rounds with a total increase in deposits of:

Φ+(1-κ)Φ + (1-κ)2Φ + (1-κ)3Φ +.............+(1-κ)nΦ=(1+(1-κ)+(1-κ)2+...+(1-κ)n)Φ

As n tends towards infinity, then since 0<k<1, we have the total increase in deposits given by Φ

This is because Z= Φ(1+(1-κ)+(1-κ)2+...+(1-κ)n+...) and hence (1-κ)Z = Φ((1-κ)+(1-κ)2+...+(1-κ)n+...).

SO z-(1-k)X = Φ

In reality, banks have the equity capital of owners (shareholders) as liabilities and will hold other sorts of assets such as government securities to protect against loan default and other risks that they face.

A model of the money supply

Using the narrow definition of money M = CH + D, where CH is money held by households. D is demand deposits.

We assume households hold currency according to CH = cD. For banks, our analysis has identified that the amount of cash they hold is CB = kD where CB is the currency reserve held by banks.

Since the total amount of currency in the system (monetary base B) must either be held by banks as reserves or by households as currency, we have:

B = CH + CB = cD + kD = (c+k)D

So D = B/c+k

We can also write: M = cD + D = (1+c)D = (1+c/c+K)B

Money supply is, therefore, a function of the monetary base B and two key behavioural parameters, c and k. For these constants, varying B changes M.

How do we control the money supply?

OPEN MARKET OPERATIONS: Monetary policymakers (central banks) typically buy/sell government bonds for a monetary base.

LENDER OF LAST RESORT: Lending directly to banks through the discount window, usually covered by bank assets. This carries an interest rate, which can be changed.

AUCTION: Central banks can announce in advance the amount of funds they will lend, and then banks will bid for them.

CHANGING INTEREST RATES: Reserves may earn interest, and the interest rate can be varied.

REQUIRED RESERVE RATIO: This is not used extensively since, usually, banks are left to choose the reserves they need.

SUMMARY

• The money supply can be defined narrowly (based on the money’s use as a medium of exchange) or more broadly (recognising that stores of value can be converted to a medium of exchange very quickly).

• Using a narrow definition of money we derived a simple model of the money supply that demonstrated the money supply multiplier and how controlling monetary base would give control over the money supply.