Ch. 7 Atomic Structure & Periodicity Study

Emission Spectra

• when a substance is exposed to a certain intensity of light or some other form of energy, the atoms absorb some of the energy (excited state atoms)

• as atom absorbs energy, 1+ electrons change their orbit(s). Bc the excited state is not stable —> electrons will return to stable ground state, through releasing energy in form of light (emission spectra)

• emission spectra of each element is unique, since certain bands of light (@ certain energies) are produced. The energy is quantized, bc only certain energies are allowed

• Ex: neon signs

Spectrum Light (electromagnetic)

• c = λν

• c = the speed of light (3.00 × 10⁸ m/s)

• λ = (Gr. letter lambda) = wavelength (meters)

• v = (Gr. Letter nu) = frequency waves/Hz = sec^-1 = Hertz = sec

• ** 1 nm = 1 × 10^-9 m ( n = “nano,” m = meters —> nanometers)

Max Planck

• dude measured heat from glowing objects & realized the energy was quantized. (energy was gained/lost in only certain amounts)

• ΔE = nhv

• n = whole # of quanta (n = 1 for 1 quantum)

• h = Planck’s Constant (6.626 × 10^-34 J/Hz)

• v (nu) = frequency (Hz)

Enistein’s Photoelectric Effect

• electrons can be ejected from metals, when light shines on the metal

• man found that this light energy is quantized: certain amount of energy must be absorbed to eject each electron

• ** Light, therefore, all electromagnetic radiation must be quantized & consists of particles, named photons

• ΔE = nhv applies to all electromagnetic radiation

where n = # of photons

• Ex. solar panels

Important Conversions

• 1 nm = 1 × 10^-9 m

freq = waves/sec —> freq = 1/sec —> Hz

• n = 1 for 1 quantum

  6.626 × 10^-34 J/Hz

• if jJ/mol change to J/photon

  1 kJ = 1 × 10³ J

  1 mol = 6.022 × 10²³ photons

• J = kg x m²/ s²

• If a problem states: 4% of the speed of light —> 4/100 —> (0.04)(3.00 × 10⁸ m/s

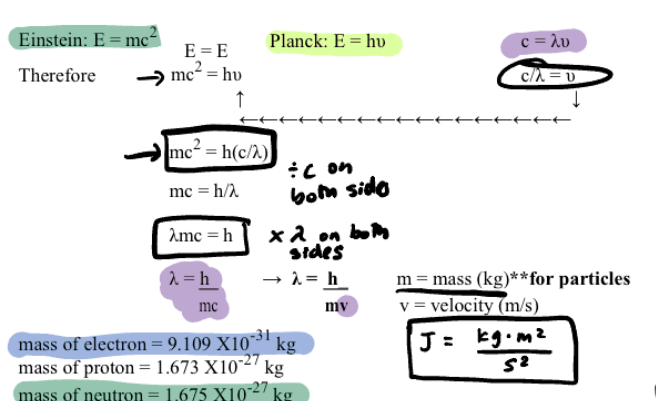
De Broglie’s Equation for Particles

useful for microscopic/fundamental particles like electrons

• If a prob states: #% the speed of light = (0.0#)(3.00 × 10⁸ m/s)

• LOOK AT IMAGE FOR FORMULAS

Bohr Model

figure out an equation to calculate the energy given off as an electron in a Hydrogen atom moves between different energy levels. (only certain orbits/layers are allowed, so it is quantized.)

• E = -2.178 × 10^-18 J ( 1 / n² final - 1 / n² initial )

  n = layer #

Schrodinger’s Quantum Mechanics

unfortunately Bohr’s Model only worked accurately on Hydrogen. Schrondiger, like De Broglie, believed that the electron showed wave-like features.

• Electron moves around the nucleus in a motion resembling a standing wave

  (waves that do not travel).

• s - orbitals ( 1 type & column #1-2 )

• p - orbitals ( 3 types & column #3-12 )

• d - orbitals ( 5 types & column #13-18 )

• f - orbitals ( 7 types & #57-71 & #89-103 )

Energy levels: are the layers of electrons ( 1, 2, 3, 4, etc. )

Sublevels: are the energy levels & orbital ( 2s, 3p, etc.)

Orbital Diagrams

Pauli Exclusion Principle: an orbital can only hold 2 electrons & they must have opposite spins

Hund’s Rule: lowest energy configuration ( most stable ) will have the max # of unpaired electrons allowed by the Pauli Principle

• “s” & “d” orbitals are similar in energy, so they can shift an electron from “s” to “d”. ( but not “s” to “p,” stop )

• f-orbitals usually fill before d-orbitals

Periodicity

Since an element’s position on the periodic table describes its electron configuration, its position allows predictions about certain properties of the element

• Atomic Radius: # of orbital layers/levels increase (going down a column), the radius will increase

• Going to the right across a row, each atom has an extra proton. This will attract the electrons more tightly, decreasing the radius. (Gold Digger Rule)

• Anions (-) have gained electrons. Since it will be harder to attract the extra electrons, anions will be larger.

• Cations (+) have lost electrons. Since it has fewer electrons to attract, its (+) nuclear charge can pull the electrons in closer, reducing radius

Ionization Energy: energy to remove an electron

• smaller the radius (electrons are more highly attracted to the nucleus), the harder it is to pull away a electron, the larger the ionization energy

  Larger the radius, the more inner electrons shield the outer electrons from the attraction of the nucleus, making it easier to remove them (small ionization energy) {Shielding Effect}

• The larger the (+) nuclear charge, the higher the ionization energy. It takes more energy to remove each successive electron.

  3^rd ionization is extremely high, since it removes an electron from a stable noble gas configuration

• The ionization energy is unusually high to remove an electron from a stable full or ½ full orbital

Electron Affinity

is the attraction energy of an atom from another electron

The smaller the radius, the stronger the attraction of the electrons, the more it wants to attract more electrons, so the higher the electron affinity.

The larger the radius, the weaker the attraction of electrons, so the smaller the electron affinity

Atoms that have full or ½ full orbitals will have unusually small electron affinities, since they are already stable & do not need to attract more electrons

**Electron affinity (-) {exothermic}, since energy is released as electrons are gained & the atom becomes more stable

Big (-) # = large electron affinity = highly exothermic

• is the ability of an atom, in a molecule_, to attract shared electrons to it

Small radius, strong attraction large electronically

Most Active Metal (Most Metallic)

(Metals lose electrons)

Loses electrons the best!

Lowest Ionization Energy

Largest Radius: Bottom/Left on the Table [Fr]

Most Active Nonmetal (Least Metallic)

(Nonmetals gain electrons)

Gains electrons the best!

Highest Electron Affinity

Smallest Radius: Top/Right (excluding noble gases)