Alternating Series Error Bound Theorem

The Alternating Series Error Bound Theorem provides a way to estimate the error when approximating the sum of an alternating series using its partial sums. This theorem is particularly useful in determining how accurate an approximation is when using a finite number of terms from an infinite series.

Definition of an Alternating Series

An alternating series is a series of the form:

where for all , and the terms are decreasing, meaning for all beyond some index . Additionally, the limit of the terms must approach zero:

The Alternating Series Test

Before discussing the error bound, it is important to note the Alternating Series Test, which states that if the series meets the criteria above (the terms are positive, decreasing, and approach zero), then the series converges.

Error Bound Theorem

Implications of the Theorem

1. Error Estimation:
   The theorem provides a clear and simple way to estimate how close the partial sum S_n actual sum S. By knowing the value of a_n+1​, you can calculate an upper bound for the error: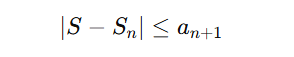

   

   This ensures that the difference between S and S_n will not exceed a_n+1​.

2. Practical Use:
   This theorem is invaluable in numerical methods and real-world applications, where approximations are often necessary. It is commonly applied in:

   • Physics: For modeling natural phenomena.

   • Engineering: In designing systems or solving problems involving series expansions.

   • Computer Science: For algorithms involving iterative approximations or simulations.

3. Convergence Assurance:
   The theorem not only establishes an error bound but also confirms the convergence of the series. As more terms are added, the error bound a_n+1​ decreases, guaranteeing that the partial sums S_n become closer to the actual sum S.

Example

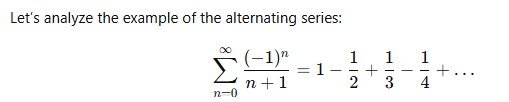
Extended Review of the Alternating Series Error Bound Theorem

1. Numerical Approximations:

   • The theorem is widely used in numerical methods, particularly in algorithms that require series approximations, such as numerical integration and solving differential equations.

2. Computer Science:

   • In computer algorithms, especially those involving iterative methods or simulations, the theorem helps in determining how many terms to compute to achieve a desired level of accuracy.

3. Physics and Engineering:

   • Many physical phenomena can be modeled using series. The error bound allows engineers and physicists to estimate the accuracy of their calculations when using series expansions.

4. Finance:

   • In financial mathematics, series are often used to model cash flows and interest calculations. The error bound can help in assessing the reliability of these models.

Additional Examples

Related Concepts

1. Convergence of Series:

   • The Alternating Series Test ensures that if the series meets the criteria (terms are positive, decreasing, and approach zero), then the series converges. This is crucial for applying the error bound theorem effectively.

2. Absolute Convergence:

   • An alternating series is said to be absolutely convergent if the series of absolute values converges. If an alternating series is absolutely convergent, it converges regardless of the order of its terms.

3. Conditional Convergence:

   • If an alternating series converges but the series of absolute values diverges, it is said to be conditionally convergent.

4. Alternating Series and Taylor Series:

   • The Alternating Series Error Bound Theorem is often applied in the context of Taylor series expansions, where the series approximates functions. Understanding the behavior of these series helps in estimating function values and their derivatives.

Practical Considerations

1. Choosing the Number of Terms:

   • When using the Alternating Series Error Bound Theorem, the choice of how many terms to include in the partial sum (S_n) depends on the desired accuracy. The smaller the value of (a_n+1), the more accurate the approximation will be.

2. Graphical Interpretation:

   • Visualizing the series can help in understanding convergence. The partial sums (S_n) can be plotted against the actual sum (S) to see how they approach each other as (n) increases.

3. Error Analysis in Numerical Methods:

   • In numerical analysis, the error bounds provided by the Alternating Series Error Bound Theorem can be critical for assessing the reliability of numerical solutions to problems, especially in iterative methods.

Conclusion

The Alternating Series Error Bound Theorem is a powerful tool in calculus that allows for the estimation of errors in approximating the sums of alternating series. By ensuring that the series meets the necessary conditions for convergence, one can effectively use the theorem to bound the error and assess the accuracy of approximations. This theorem has wide-ranging applications in mathematics, physics, engineering, and computer science, making it an essential concept for students and professionals alike.

Summary of Key Points

• Definition: The theorem provides an error bound for approximating the sum of an alternating series using its partial sums.

• Conditions: The series must have positive, decreasing terms that approach zero.

• Error Bound: The error in approximating the sum is less than or equal to the absolute value of the first neglected term.

• Applications: Useful in numerical methods, computer science, physics, engineering, and finance.

• Related Concepts: Convergence, absolute and conditional convergence, and Taylor series.

By understanding and applying the Alternating Series Error Bound Theorem, one can gain valuable insights into the behavior of alternating series and their approximations, leading to more accurate calculations and analyses in various fields.