All Data Structures & Algorithms

Selection Sort Definition

a sorting algorithm that treats the input as two parts, sorted and unsorted, and repeatedly selects the proper next value to move from the unsorted part to the end of the sorted part.

Selection Sort Algorithm

for i in range(len(numbers) - 1):

# Find index of smallest remaining element

index_smallest = i

for j in range(i + 1, len(numbers)):

if numbers[j] < numbers[index_smallest]:

index_smallest = j

# Swap numbers[i] and numbers[index_smallest]

temp = numbers[i]

numbers[i] = numbers[index_smallest]

numbers[index_smallest] = temp

Insertion Sort Definition

a sorting algorithm that treats the input as two parts, sorted and unsorted, and repeatedly inserts the next value from the unsorted part into the correct location in the sorted part.

Insertion Sort Algorithm

for i in range(1, len(numbers)):

j = i

# Insert numbers[i] into sorted part

# stopping once numbers[i] in correct position

while j > 0 and numbers[j] < numbers[j - 1]:

# Swap numbers[j] and numbers[j - 1]

temp = numbers[j]

numbers[j] = numbers[j - 1]

numbers[j - 1] = temp

j = j - 1

Quick Sort Definition

a sorting algorithm that repeatedly partitions the input into low and high parts (each unsorted), and then recursively sorts each of those parts.

Quick Sort Algorithm

def partition(numbers, i, k):

# Pick middle value as pivot

Midpoint = i + (k - i) // 2

Pivot = numbers[midpoint]

# Initialize variables

done = False

l = i

h = k

while not done:

# Increment l while numbers[l] < pivot

while numbers[l] < pivot:

l = l + 1

# Decrement h while pivot < numbers[h]

while pivot < numbers[h]:

h = h - 1

# If there are zero or one items remaining,

# all numbers are partitioned. Return h

if l >= h:

done = True

else:

# Swap numbers[l] and numbers[h],

# update l and h

temp = numbers[l]

numbers[l] = numbers[h]

numbers[h] = temp

l = l + 1

h = h - 1

return h

Merge Sort Definition

a sorting algorithm that divides a list into two halves, recursively sorts each half, and then merges the sorted halves to produce a sorted list.

Merge Sort Algorithm

def algorithm(numbers, i, j, k):

# Create temporary list merged_numbers

# Initialize position variables

# Add smallest element to merged numbers

while left_pos <= j and right_pos <= k:

if numbers[left_pos] <= numbers[right_pos]:

merged_numbers[merge_pos] = numbers[left_pos]

left_pos = left_pos + 1

else:

merged_numbers[merge_pos] = numbers[right_pos]

right_pos = right_pos + 1

merge_pos = merge_pos + 1

# If left partition not empty, add remaining elements

while left_pos <= j:

merged_numbers[merge_pos] = numbers[left_pos]

left_pos = left_pos + 1

merge_pos = merge_pos + 1

# If right partition not empty, add remaining elements

while right_pos <= k:

merged_numbers[merge_pos] = numbers[right_pos]

right_pos = right_pos + 1

merge_pos = merge_pos + 1

# Copy merge number back to numbers

for merge_pos in range(merged_size):

numbers[i + merge_pos] = merged_numbers[merge_pos]

Radix Sort Definition

a sorting algorithm designed specifically for integers. The algorithm makes use of a concept called buckets and is a type of bucket sort.

Radix Sort Algorithm

Algorithm(array, arraySize) {

buckets = create array of 10 buckets

// Find the max length, in number of digits

maxDigits = RadixGetMaxLength(array, arraySize)

// Start with the least significant digit

pow10 = 1

for (digitIndex = 0; digitIndex < maxDigits; digitIndex++) {

for (i = 0; i < arraySize; i++) {

bucketIndex = abs(array[i] / pow10) % 10

Append array[i] to buckets[bucketIndex]

}

arrayIndex = 0

for (i = 0; i < 10; i++) {

for (j = 0; j < buckets[i]⇢size(); j++)

array[arrayIndex++] = buckets[i][j]

}

pow10 = 10 * pow10

Clear all buckets

}

}

Shell Sort Definition

a sorting algorithm that treats the input as a collection of interleaved lists, and sorts each list individually with a variant of the insertion sort algorithm. Uses gap values to determine the number of interleaved lists.

Shell Sort Algorithm

def algorithm(numbers, start_index, gap):

for i in range(start_index + gap, len(numbers), gap):

j = i

while (j - gap >= start_index) and (numbers[j] < numbers[j - gap]):

temp = numbers[j]

numbers[j] = numbers[j - gap]

numbers[j - gap] = temp

j = j - gap

Bubble Sort Definition

a sorting algorithm that iterates through a list, comparing and swapping adjacent elements if the second element is less than the first element. Uses nested loops.

Bubble Sort Algorithm

Algorithm(numbers, numbersSize) {

for (i = 0; i < numbersSize - 1; i++) {

for (j = 0; j < numbersSize - i - 1; j++) {

if (numbers[j] > numbers[j+1]) {

temp = numbers[j]

numbers[j] = numbers[j + 1]

numbers[j + 1] = temp

}

}

}

}

Quickselect

an algorithm that selects the k^th smallest element in a list. Ex: Running on the list (15, 73, 5, 88, 9) with k = 0, returns the smallest element in the list, or 5.

Quickselect algorithm

def algorithm(numbers, start_index, end_index, k):

if start_index >= end_index:

return numbers[start_index]

low_last_index = partition(numbers, start_index, end_index)

if k <= low_last_index:

return quickselect(numbers, start_index, low_last_index, k)

return quickselect(numbers, low_last_index + 1, end_index, k)

Heap Sort

a sorting algorithm that takes advantage of a max-heap's properties by repeatedly removing the max and building a sorted array in reverse order.

Heap Sort Algorithm

Algorithm(numbers, numbersSize) {

//Heapify numbers

for (i = numbersSize / 2 - 1; i >= 0; i--) {

MaxHeapPercolateDown(i, numbers, numbersSize)

}

for (i = numbersSize - 1; i > 0; i--) {

Swap numbers[0] and numbers[i]

MaxHeapPercolateDown(0, numbers, i)

}

}

Bucket Sort

a numerical sorting algorithm that distributes numbers into buckets, sorts each bucket with an additional sorting algorithm, and then concatenates buckets together to build the sorted result.

Bucket Sort Algorithm

Algorithm(numbers, numbersSize, bucketCount) {

if (numbersSize < 1)

return

buckets = Create list of bucketCount buckets

// Find the maximum value

maxValue = numbers[0]

for (i = 1; i < numbersSize; i++) {

if (numbers[i] > maxValue)

maxValue = numbers[i]

}

// Put each number in a bucket

for each (number in numbers) {

index = floor(number * bucketCount / (maxValue + 1))

Append number to buckets[index]

}

// Sort each bucket

for each (bucket in buckets)

Sort(bucket)

// Combine all buckets back into numbers list

result = Concatenate all buckets together

Copy result to numbers

}

Pre-Order Traversal

In this traversal method, the root node is visited first, then the left subtree and finally the right subtree.

If a binary tree is traversed in this method, it can be used to duplicate the tree.

Post-order Traversal

In this traversal method, the root node is visited last, hence the name. First we traverse the left subtree, then the right subtree and finally the root node.

If a binary tree is traversed in this method, the tree can be deleted.

In-order Traversal

In this traversal method, the left subtree is visited first, then the root and later the right sub-tree. We should always remember that every node may represent a subtree itself.

If a binary tree is traversed in this method, the output will produce sorted key values in an ascending order.

Bubble Sort, Selection Sort, Insertion Sort Time Complexity

Average = Θ(n^2 )

Big-O worst = O(n^2 )

Fast = No

Quick Sort Time Complexity

Average = Θ(n log(n))

Big-O worst = O(n^2 )

Fast = Yes

Bucket Sort Time Complexity

Average = Θ(n)

Big-O worst = O(n^2 )

Fast = Yes

Heap Sort, Merge Sort Time Complexity

Average = Θ(n log(n))

Big-O worst = O(n log(n))

Fast = Yes

Radix Sort Time Complexity

Average = Θ(n)

Big-O worst = O(n)

Fast = Yes

A functions whose cost scales linearly with the size of the input

O(n)

Iterating over a collection of data once often indicates an ______ algorithm. (alphabet for-loop example)

O(n)

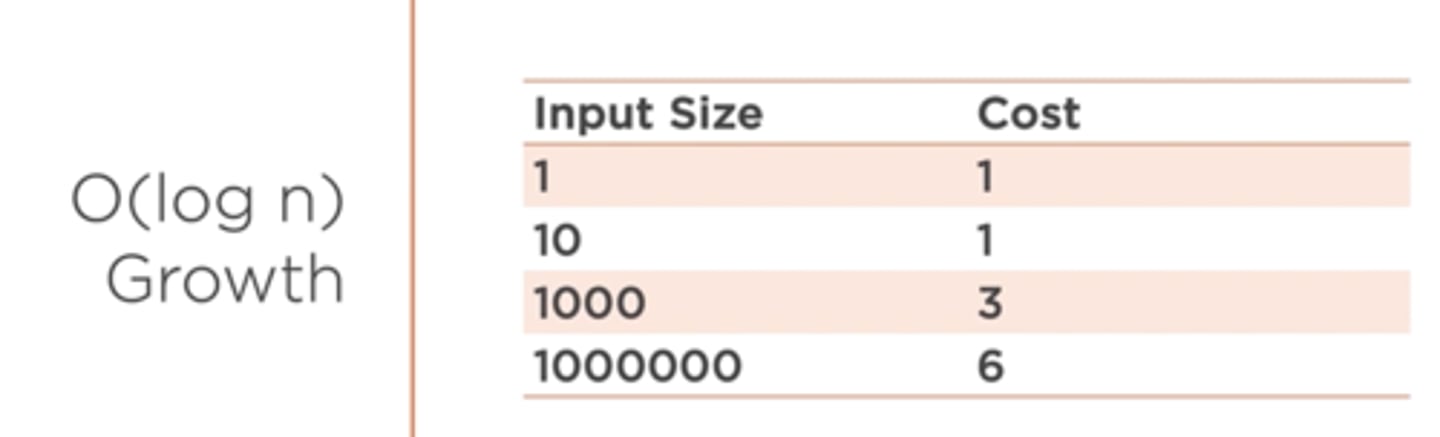
A functions whose cost scales logarithmically with the input size

O(log n)

Which type of function works by breaking down large problem into smaller and smaller chunks?

recursive

As the size of the input grows the cost of the algorithm does not increase at the same rate. The overall cost of performing an operation on 1,000,000 items is only twice that of performing the operation on 1,000 items.

O(log n)

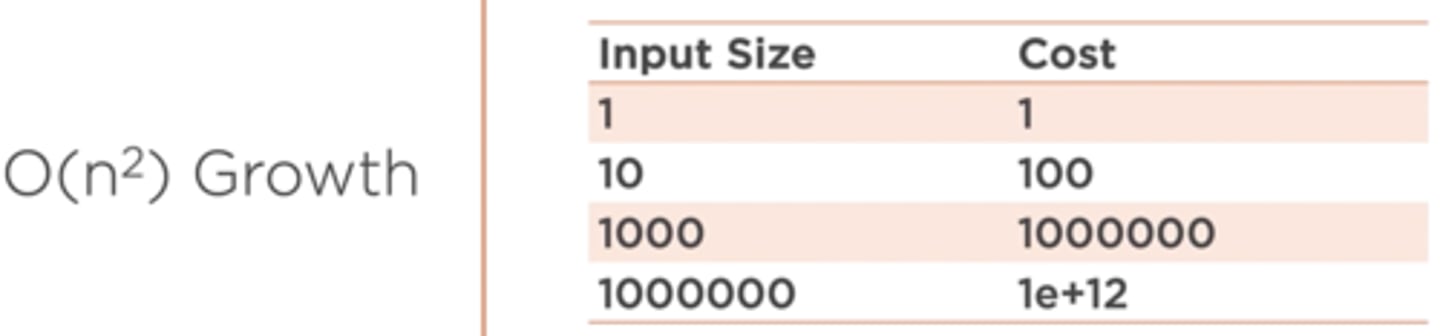
A function that exhibits quadratic growth relative to the input size

O(n^2)

An example of this type of function is doubly nested loop

O(n^2)

Which type of function gets really expensive really quickly?

O(n^2)

A function that has two inputs that contribute to growth

O(nm)

An example of this type of function is when there is a nested loop that iterates of two distinct collections of data

O(nm)

Are Big-O cases used in the best or worst situations?

Worst

Which statement is static?

readonly Contact[] contacts = new Contact[];

readonly Contact contacts = new Contacts[100];

readonly Contact contacts = new Contacts[100];

A container where data is stored in nodes consisting of a single data item and a reference to the next node

Linked List

A ______ is a container where nodes of data are linked together into a list

Linked List

Linking together complex nodes into a single structure

Linked List

Each link in a chain for a linked lists is called a ______

node

What two things do nodes contain?

1. the value

2. reference to next item in the list

Give a coded example on how to create a 3 chained linked list of nodes.

Node head = new Node(1);

head.Next = new Node(2);

head.Next.Next = new Node(3);

A list where we start at the first node and follow the chain of nodes iterating over each until we get to the end

Singly Linked List

A list that builds on the singly linked list by adding reverse iteration.

Doubly Linked List

Give a coded example on how to create a doubly linked list

Node node1 = new Node(1);

Node node2 = new Node(2);

Node node3 = new Node(3);

node1.Next = node2;

node2.Previous = node1;

node2.Next = node3;

node3.Previous = node2;

The first and last nodes of a doubly linked list should have a value of ______

null

Adds a value to the beginning of the list

AddHead

Adds a value at the end of the linked list

AddTail

Finds the first node whose value equals the provided argument

Find

Returns true if the specified value exists in the list, false otherwise

Contains

Removes the first node on the list whose value is equal to the argument

Remove

A doubly linked list where the values are inserted and sorted in order

Sorted List

Adds the specified item to the linked list in the sort order of the item type

Add

A way of organizing, storing, and performing operations on data

Data Structure

A data structure that stores subitems, with a name associated with each subitem.

record

A data structure that stores an ordered list of items, with each item is directly accessible by a positional index.

Array

A data structure that stores ordered list of items in nodes, where each node stores data and has a pointer to the next node.

linked list

A data structure in which each node stores data and has up to two children, known as a left child and a right child.

binary tree

A data structure that stores unordered items by mapping (or hashing) each item to a location in an array.

hash table

A tree that maintains the simple property that a node's key is greater than or equal to the node's childrens' keys.

max heap

A tree that maintains the simple property that a node's key is less than or equal to the node's childrens' keys.

min heap

A data structure for representing connections among items, and consists of vertices connected by edges.

graph

This represents an item in a graph.

vertex

This represents a connection between two vertices in a graph.

edge

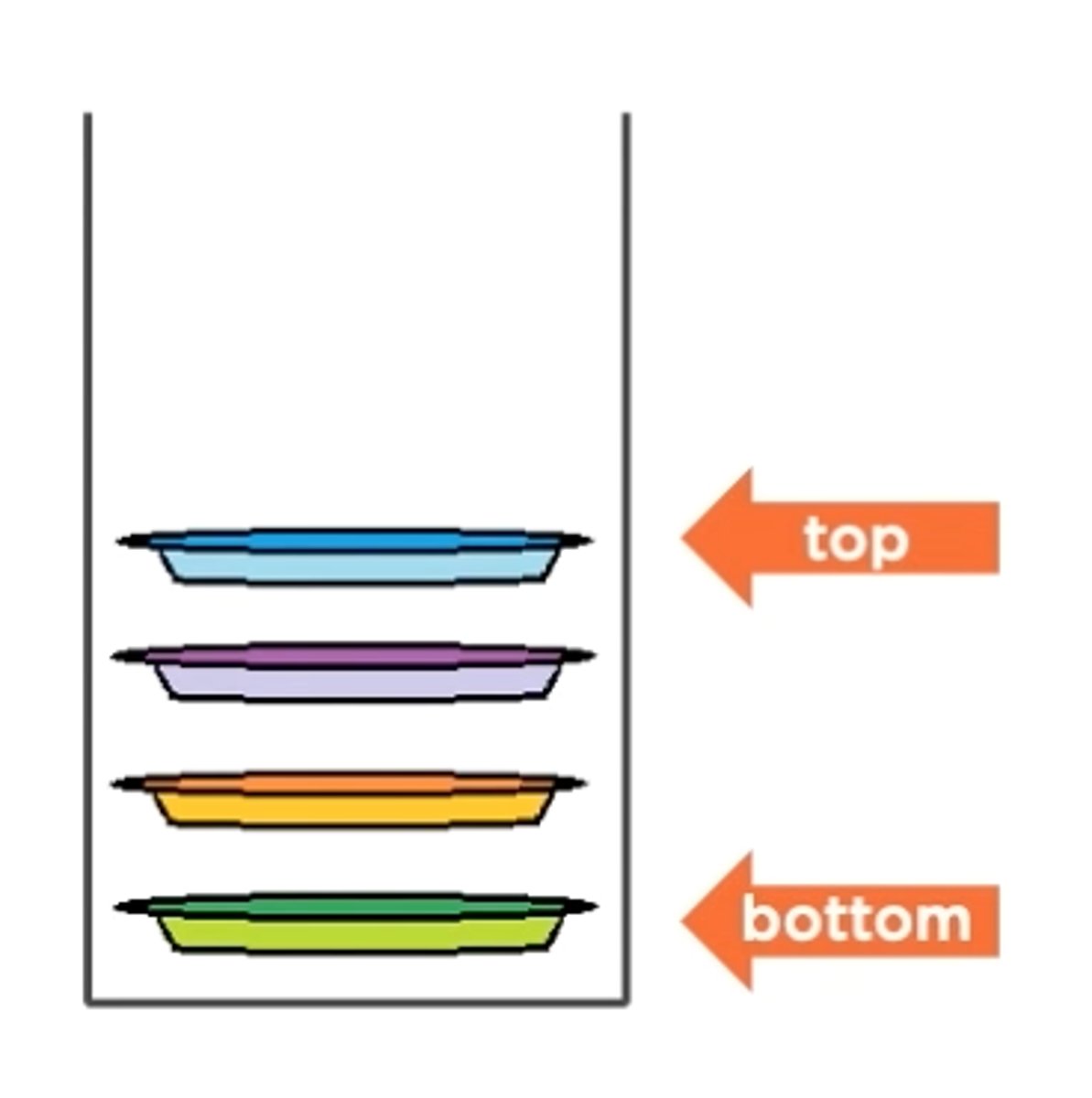
A Last-in, First-out (LIFO) data container

Stack

When something is retrieved from a stack, does it come from the top or bottom of the stack?

Top

A First-in, First-out (FIFO) container

Queue

When something is removed from a queue, does it come from the head or the tail?

Head

When something is added to a queue, does it get added to the head or the tail?

Tail

A queue-like container which is both First-in, First-out and Last-in, Last-out

Doubly Ended Queue (deque)

Which type of function allows for items to be added or removed from the beginning or end?

Doubly Ended Queue (deque)

A data structure where nodes have parent-child (1:N) relationship

Tree

Each node in a Tree has at least ______ parent, but the number of children depends on the type of tree

one

Every node in a tree has how many parents?

one

Every part of a tree spawns how many children?

0 or more

Nodes that have no children are called what?

Leaf nodes

How many data items does each node on a tree contain?

one

At most how many children can each node have in a binary tree?

two

The maximum number of children that each node can have

Degree

The maximum amount of edges between that node and a leaf

Height

When smaller values are added to this tree smaller values are added to the left

Binary Search Tree

The smallest value in a binary search tree will be on the bottom most ______, while the largest value will be on the bottom most ______

left

right

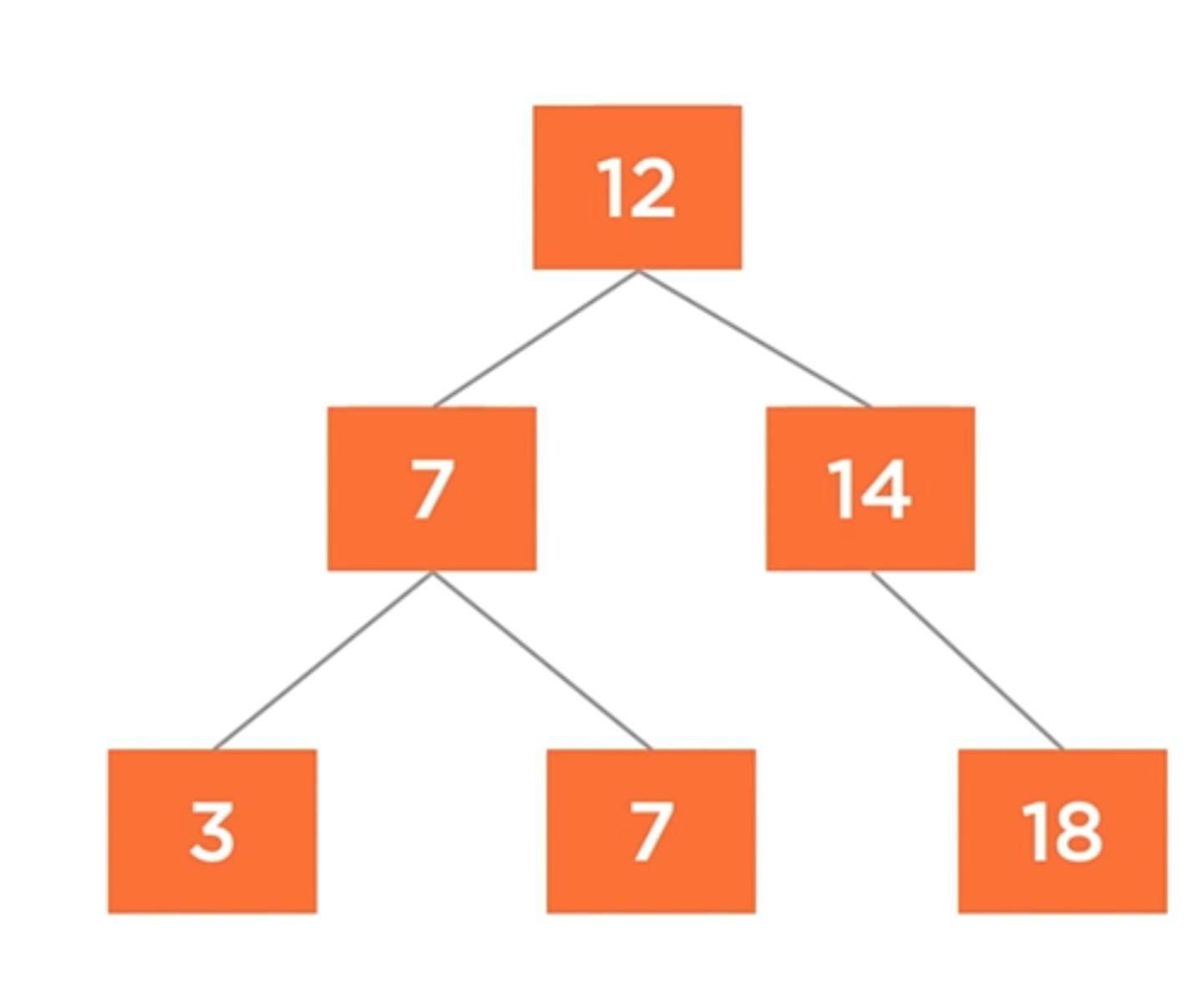
The insertion complexity on average of a binary search tree

O(long n)

The insertion complexity with the worst case of a binary search tree

O(n)

The node is visited before it's children

Pre-order

The left child is visited before the node, then the right child

In-order

The left and right children are visited before the node

Post-order

An example of why pre-order traversals are useful

To create an identical copy of a tree

What are in-order traversals useful for?

Sorting trees from least to greatest

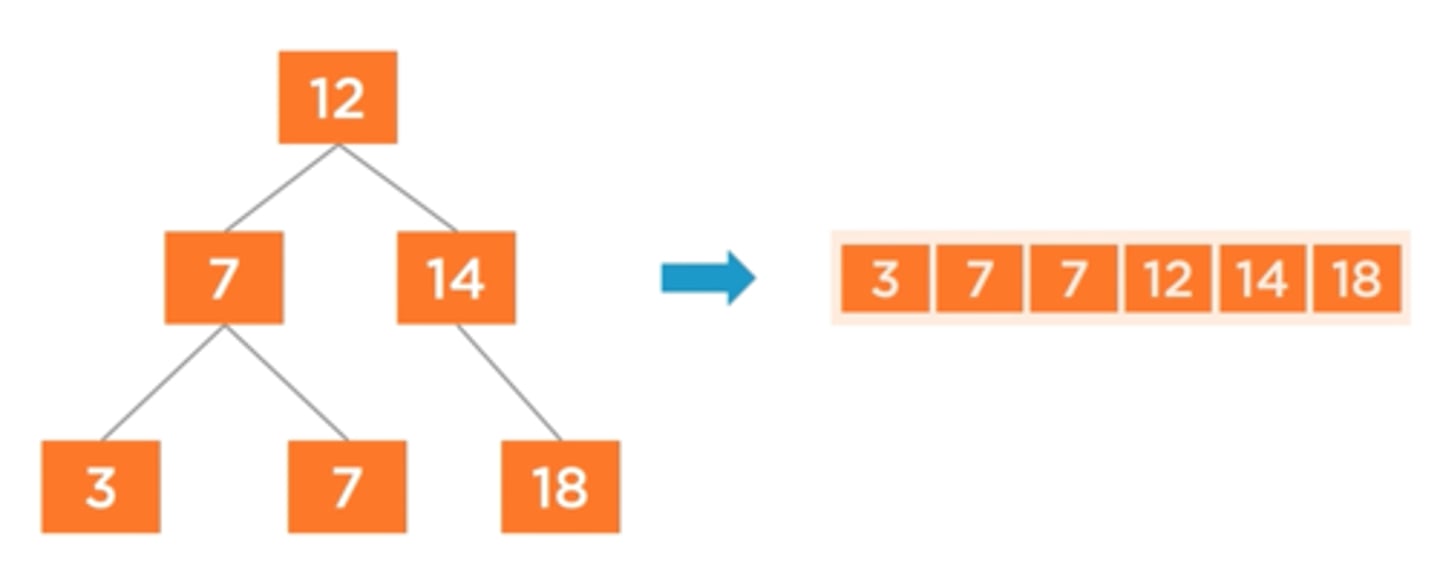
What are post-order traversals useful for?

To delete every node in a tree

The average case, best case and worst case for Traversal Complexity

O(n)

Searching in Binary Search Tree

O(log n)

How can a leaf node be removed from a tree?

Unlinking the node

How can a node with One Child be removed from a tree?

Promote the child

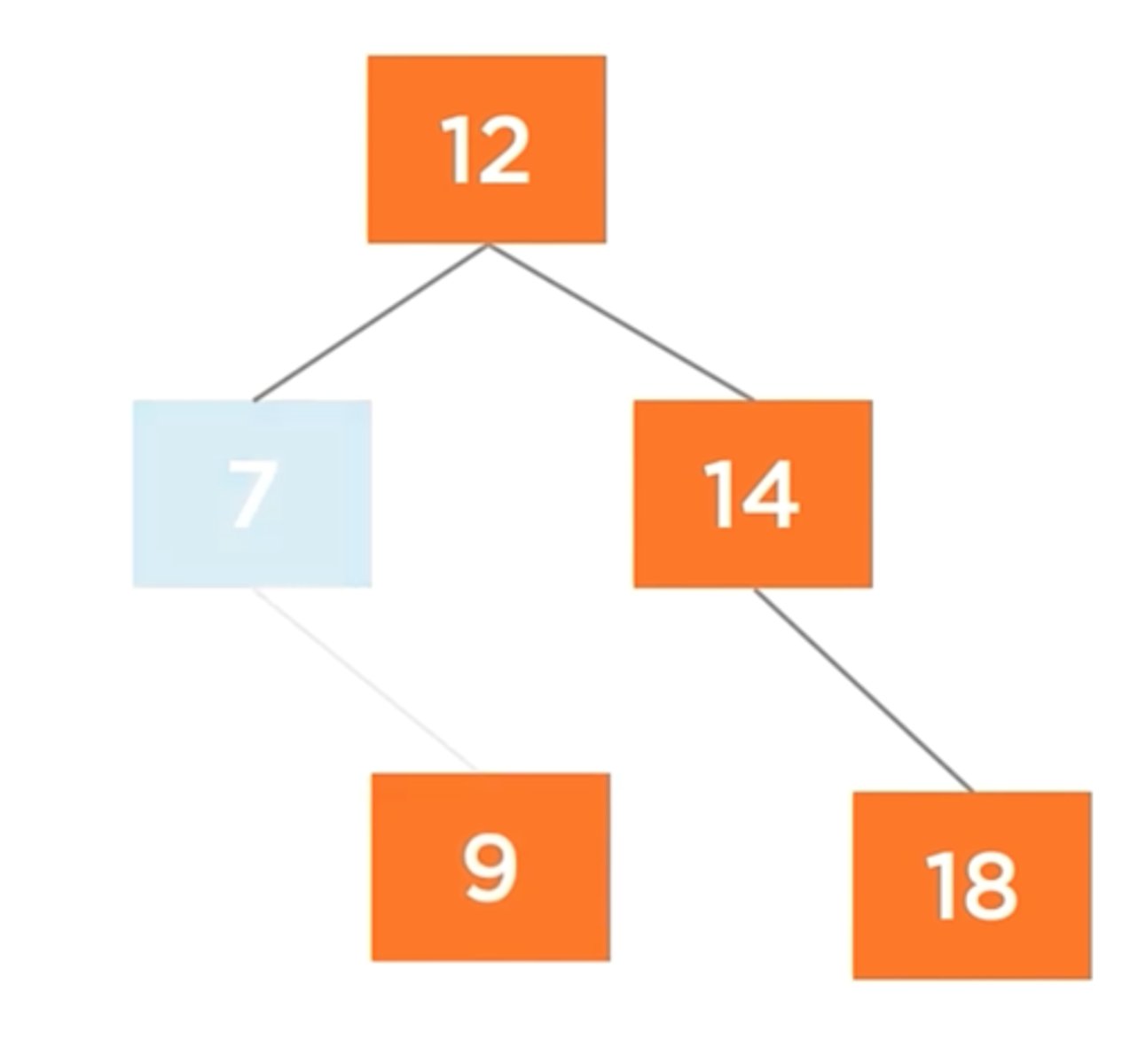
How can a node with Two Children be removed from a tree?

Move the successor's child up to the root node.

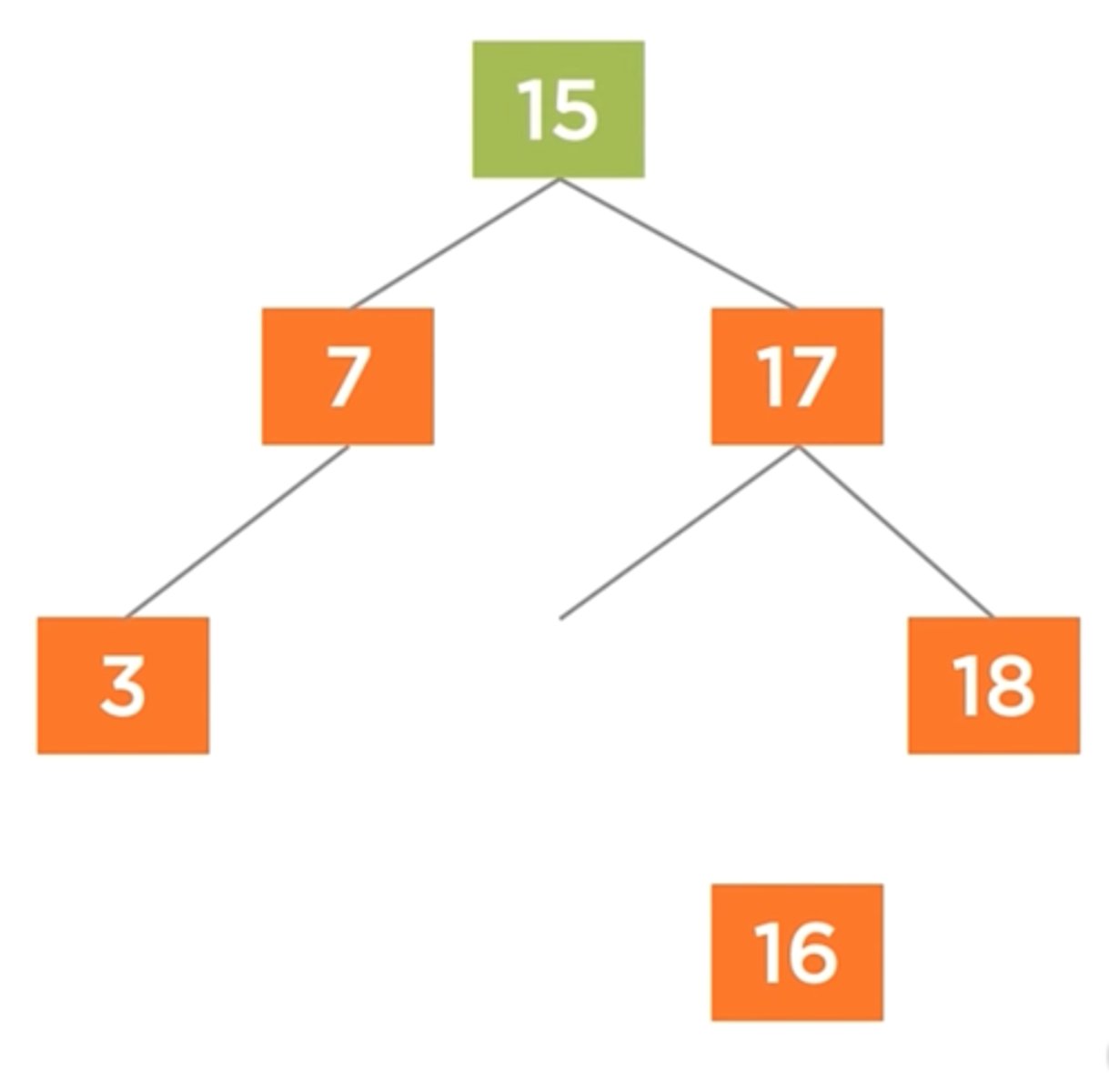
Removal Complexity in a Binary Tree

O(log n)