Ch.3 Stats Vocab

univariate data

one set of data

• ex: boxplot, ogive, histogram, timeplot, dotplot, ribbon chart, pie chart

• describe w/ SOCS

bivariate data

two quantitative data sets

• always graph data on scatterplots!

• ex: tables, scatterplots, correlation, LSRL

• describe w/ FODS (form, outliers, direction, strength)

scatterplot

shows relationship between two QUANTITATIVE variables that were measured on the same individual

• has a horizontal & vertical axis

• each individual = one point

describe distribution (BIVARIATE)

form, strength, direction, outliers/deviations

• IN CONTEXT!!!!

form

general shape of the scatterplot

• linear or nonlinear

• nonlinear = curved, exponential, cluster, multiple clusters, etc

strength

describes the association between the two variables; how closely related are the two variables

• ex: strong, moderate, weak

• ALWAYS use the r-value

direction

the type of association; the region the scatterplot appears to be going to

• can be:

  • positive - increases in explanatory variable = increases in response variable

  • negative - increases in explanatory variable = decreases in response variable

  • none/no - increases in explanatory variable = no predicted region the scatterplot is going toward

outliers/deviations

any points that don’t really fit the pattern, have large residuals

• this is measured approximately

• may decrease or increase a correlation coefficent

formula for describing distribution

There is a strong/moderate/weak (r = a) positive/negative linear/nonlinear association between variable x and variable y. In general, as the explanatory variable increases, the response variable increases/decreases.

correlation coefficient (r)

measure of the direction and strength of the association

• only used for LINEAR relationships

• does not depend on units of measurement (can interchange variables)

• between -1 and 1

• sensitive to outliers

• does NOT mean causation or form

• requires both explanatory and response variables

calculate r-value

product of the z-scores (x and y) over n-1

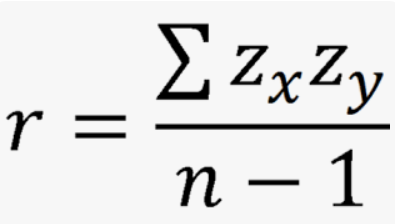
regression line

summarizes the relationship between two variables, but only in a specific setting: when one variable helps explain the other

• ŷ = a + bx

• ŷ = y-hat, the predicted value of the response variable

• x = the explanatory variable

a

y-intercept

b

slope, can be calculated w/

• r × (S_y/S_x)

least-squares regression line/LSRL

the line of best fit; the regression line that makes the sum of the squared residuals a small as possible

• NOT the same as a regression line; it is a very specific type of regression line

• always passes through (x̄, ȳ)

how to find LSRL

• ŷ = a + bx

• (x̄, ȳ) is always on the line

• slope = r × (S_y/S_x)

• plug and chug

  • plug in mean coordinates into ur general equation

  • solve for a

  • write out equation and define variables

residuals

the leftovers or prediction errors in the vertical axis; y - ŷ = actual - predicted

• positive —> y > ŷ

  • actual is higher than predicted

• negative —> y < ŷ

  • actual is lower than predicted

• none —> y = ŷ

  • actual is the same as predicted

slope in context formula

On average, or every increase in 1 (unit of explanatory/x variable), the predicted (response variable) increases/decreases by slope (unit of response/y variable)

y-intercept in context formula

When the (explanatory/x variable) is at 0 (unit of explanatory variable), the predicted (response/y variable) is at “a” (unit of response variable)

extrapolation

the use of the regression line for a prediction far outside of the interval of the x-values used to create the line

• often not accurate

residual plot

a scatterplot that displays the residuals on the vertical axis and explanatory variable on the horizontal axis

• linear model = appropriate if

  • no obvious patterns

  • relatively small in size

  • even scatter above and below x-axis

standard error (S_e)

the average size of a residual; measures how far, on average, each value differs from the predicted

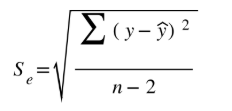
S_e in context formula

On average, the predicted (response variable) differs from the actual (response variable) by about S_e (units of response variable)

Total Sum of Squares of Errors (SST) or Sum of Squares Total

the overall measure of variation in the y-values

• uses y-bar, not y-hat

• sum of the difference between the actual and average squared

• on a scatterplot —> draw average as a horizontal line and fine difference

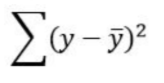
standard deviation from average (S_y)

measures how far, on average, each value differs from the mean

• Sy = square root of variance

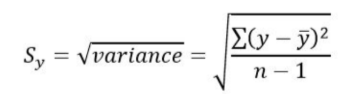
Sum of the Squares of Errors (SSE) or Residuals

amount of variation in the residuals

• uses y-hat, not y-bar

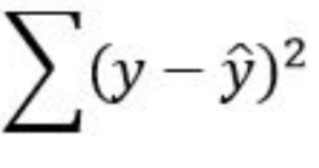
R-squared/Coefficient of Determination

measures the percent reduction in the sum of squared residuals when using the LSRL to make predictions, rather than the mean value of y

• the percent of the variablity in the response variable that is accounted by the LSRL

• can also use the correlation coefficient squared

• can only be applied to LINES, not just any curve

• influential points that lie near LSRL —> increase the value

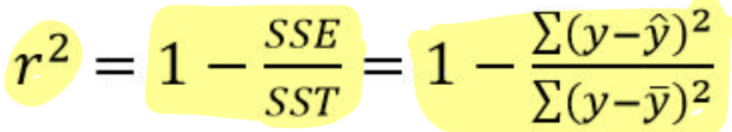
r-squared in context formula

the amount of variation that has been explained/accounted for by the linear relationship between (response and explanatory variables) is __%

or

___% of the variation in the (response variable) can be explained by/accounted for by the linear relationship with (explanatory variable)

learn how to read computer regression output

be able to find

• the slope b

• the y intercept a

• the values of s

• the value of r²

is the linear model appropriate

1. residual plot —> scattered randomly and evenly

2. r² —> high percentage

3. sum of residuals squared —> small total residuals

comparing models criteria

when comparing two different LSRL models, make sure to list the numbers and observations for both models when explaining.

• must use these three: residual plot, r², and SSE (sum of residuals squared)

• optional: comparing point predictions (within range?), nicer scatterplot (curved or not curved?)

general formula for comparing LSRL models

1. general statement - Model #A does a better job at predicting the response variable with explanatory variable.

2. three evidence in context with justification

   1. SSE - There is less amount of errors with Model #A (SSE Model #A versus SSE Model #B)

   2. R² - There is more variation explained with Model #A (R² %) than Model #B (R² %).

   3. Residual plot - The residual plot for Model #A indicates a better model because ___ (more scattered? even distribution? less cluster? less pattern?), while Model #B has __ (less scatter? more clusters? more pattern?).

high leverage

points that are extreme in the x direction

influential

points that, if removed, substantially change the regression line

• change in slope, y-intercept, correlation, coefficient of determination, or increases in standard deviation

exponential growth

when a variable increases by multiplication by a fixed amount as time increases by a fixed amount

transforming the data

applying another function (ex: logarithm or square root) to a quantitative variable

• must be applied to ALL inputs of that variable

• typically done with the intention of “linearizing” data

finding residuals of transformed data (explanatory data)

plug values in like normal, making sure to correctly enter the x-value into the function

• ex:

  •  ŷ = a + b × log(x) —> y - ŷ

  •  ŷ = a + b × e^x  —> y - ŷ

  •  ŷ = a + b × x² —> y - ŷ

finding residuals of transformed data (response variable)

plug in x-values into function (if applicable), but makes sure to “undo” the function for the y-variable

• compare apples to apples; dont want to compare the exponent to the real value

• ex:

  •  log(ŷ) = a + b × log(x) —> y - 10^ŷ

  •  e^ŷ = a + b × x —> y - ln(ŷ)

  •  (ŷ)² = a + b × x² —> y - sqrt(ŷ)