4. Sequences, Series, and Convergence

Convergence

(∀ε > 0)(∃N ∈ N)(∀n ≥ N)|aₙ − L| < ε.

Explain the defenition (∀ε > 0)(∃N ∈ N)(∀n ≥ N)|aₙ − L| < ε

ε - epsilon (an arbitrarily small number)

L - the limit

|aₙ − L| - the difference between a term in the sequence and the limit

aₙ converges to L, if for all ε > 0, there is some N ∈ N such that whenever n > N, we have |aₙ − ℓ| < ε

Convergence topological defenition

(∀ε > 0)(∃N ∈ N)(∀n ≥ N)aₙ ∈ Vϵ(a)

the sequence term xₙ lies inside the epsilon neighbourhood of a (a is the limit)

epsilon-neighborhood of a definition

Given a real number a ∈ R and a positive number ϵ > 0, the set

Vϵ(a) = {x ∈ R : |x − a| < ϵ}

diagramatic representation of the e-neighborhood of a

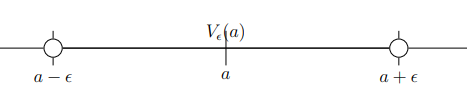
expand |a - L| < ϵ

-ϵ < a - L < ϵ

L - ϵ < a < L + ϵ

Template proof the xₙ → x

1. let ϵ > 0 be arbitrary

2. Demonstrate a choice for N ∈ N

3. Now, show that N actually works

4. Assume n ≥ N

5. with N well chosen, you should be able to get to |xₙ - x| < ϵ

Prove that 1/√n → 0

general case

1. let e >0 be arbitrary, solve 1/√n < e for 

2. n > 1/e² 

3. for every e > 0, we can pick N with N > 1/e²  (because the natural numbers are unbounded)

4. (∀n ≥ N) 1/√n < ϵ

5. therefore, (∀e>0)(∃n ∈ N)(∀n ≥ N)(|1/√n - 0| < e)

defenition of a bounded sequence

(∃L, U ∈ R)(∀n ∈ N)L ≤ an ≤ U

Prove A sequence (an) is bounded if and only if (∃C ∈ R)(∀n ∈ N)|an| ≤ C

We assume that (∃C ∈ R)(∀n ∈ N)|aₙ| ≤ C

(∃C ∈ R)(∀n ∈ N) − C ≤ aₙ ≤ C.

By setting L = −C and U = C, we can see that

→(∃L, U ∈ R)(∀n ∈ N)L ≤ aₙ ≤ U.

now we assume

(∃L, U ∈ R)(∀n ∈ N)L ≤ aₙ ≤ U.

We set C = max{|L|, |U|}

(∃L, U ∈ R)(∀n ∈ N)L ≤ aₙ ≤ U

→(∃C ∈ R)(∀n ∈ N)|aₙ| ≤ C