Derivatives and Integrals

∫sin x dx

-cos x + c

∫cos x dx

sin x + c

∫sec^2 x dx

tan x + c

∫sec x tan x dx

sec x + c

d/dx sin x

cos x

d/dx cos x

-sin x

d/dx tan x

sec^2 x

d/dx sec x

sec x tan x

∫tanx dx

ln|secx| + C

∫secx dx

ln|secx + tanx| + C

∫ cos^2x dx

1/2x+1/4sin2x + C

∫ sin^2x dx

1/2x - 1/4sin2x + C

∫ e^x dx

e^x + C

∫ a^x dx

a^x/ln a +C

∫ 1/x dx

ln|x| +C

∫ coshx dx

sinhx + C

∫ sinhx dx

coshx + C

d/dx logb(x)

1/x ln(b)

∫e^x + 1/x dx

e^x + ln|x| + C

Average Value Theorem

MVT for Integrals: f(c)=f ave

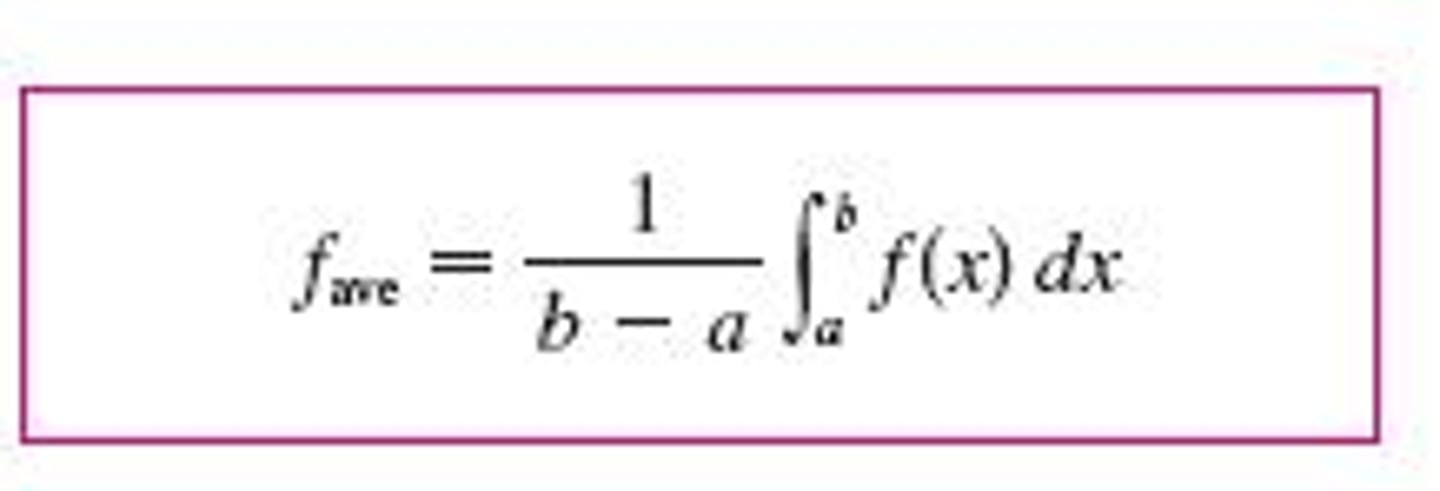
if the bounds are switch in a definite integral

the definite integral becomes negative

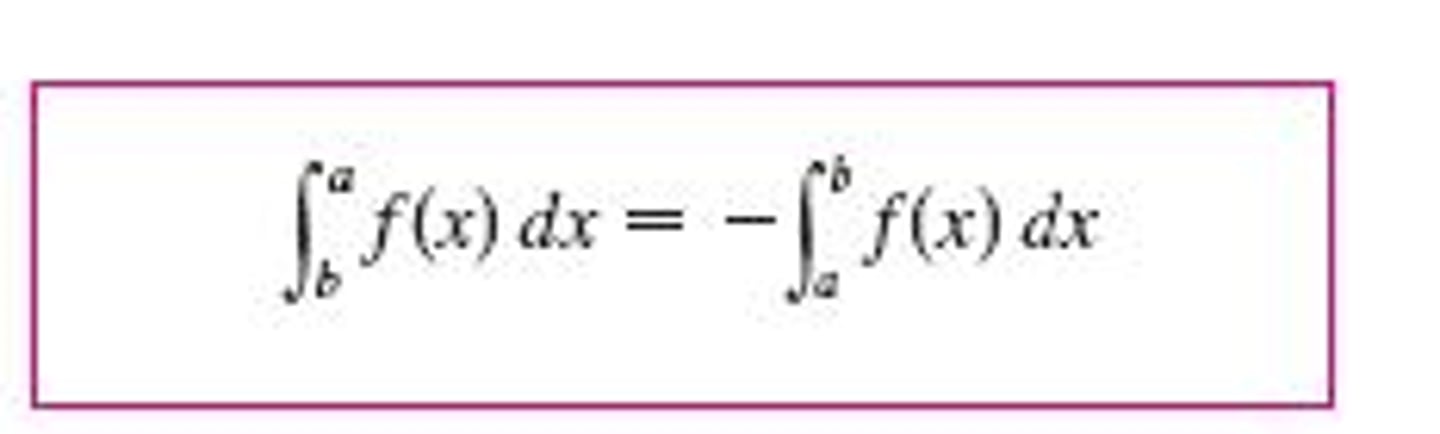
a(t) = v'(t) dt, thus

v(t) = ∫ a(t)

net change theorem

Definite Integrals w/ u-substitution

always be sure to change the bounds from values of x to values of u

Hooke's Law

states the the force required to maintain a spring stretched x units beyond its natural length is proportional to x:

f(x) = k x , where k is a positive 'spring' constant

1) Force given in problem, is f(x)

2) x is the length given

3) if its given in inches, always convert to feet (e.g 4 inches=1/3 feet)

Use definite integral to solve, setting a=0 and b=length in which you're solving for

Find c such that f(c)=f ave

Change integral from f(x) to f(c) to find c

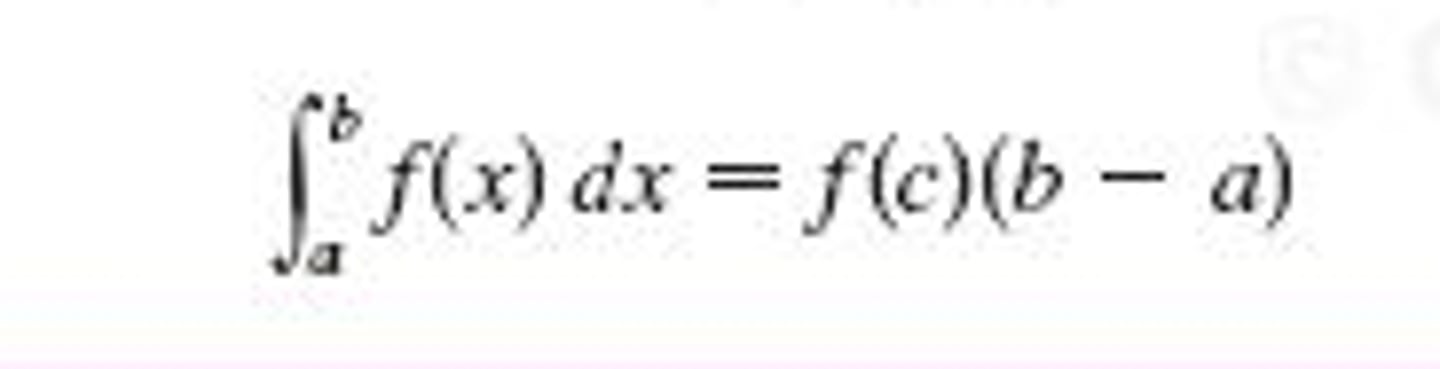
d/dx 1/x

-x⁻² = -(1/x²)

d/dx 5^(-1/x)

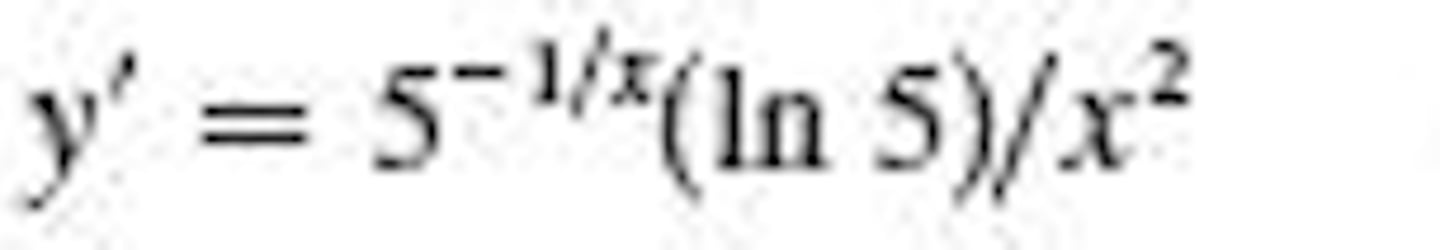
d/dx 2^(sinπx)

Using Chain Rule property d/dx aⁿ = aⁿ (ln a)

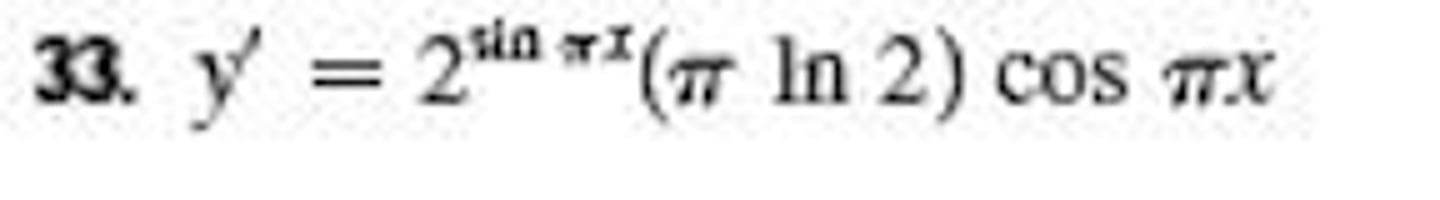
y' and y" cos(x²)

d/dx (cosx)² = 2(cosx)(-sinx) = -2(cosx)(sinx) = -sin(2x) (double angle identity)

d/dx -sin(2x) = -cos(2x)(2) = -2(cos(2x))

d/dx tan⁻¹

1/(1+x²)

d/dx cos⁻¹

-1/(√1-x²)

d/dx sin⁻¹

1/(√1-x²)

d/dx cot

-csc²x

d/dx cscx

-cscx cotx

∫ e(^x+e^x)

Use u-substitution

u=e^x

du=e^x dx

∫ e^u du = e^u + c = e^(e^x)+c

∫ e²

e²x + c

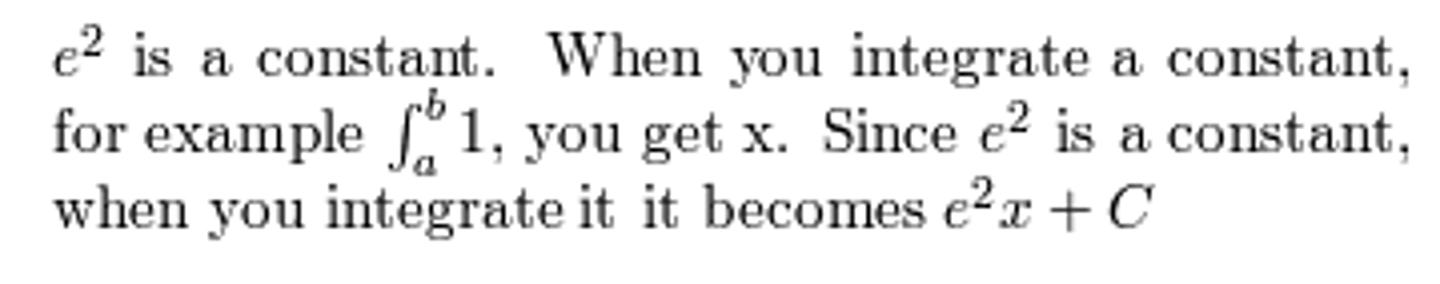
∫1/(1+eⁿ) dx

-ln|e⁻ⁿ+1|+C

multiply num. and den. by e⁻ⁿ and let u=e⁻ⁿ+1

f is continuous and ₁∫³ f(x) dx=8, show that f takes on the value 4 at least once in the interval [1,3]

8 = f(c)(3-1)

8 = f(c)(2)

8/2 = f(c) = 4

According to the FTC1 ⁿ∫₁ 1/(t³+1)dt equals?

1/(n³+1)

F'(x) = d/dx [ⁿ∫₁ 1/(t³+1) dt] = f(x)

v(t) = ∫ a(t) dt, thus

d(t) = ∫ v(t) dt