ACC GEOMETRY MIDTERM VOCAB

slope formula

slope intercept formula

y=mx+b

point slope formula

y-y₁=m(x-x₁)

standard form (+ rules)

Ax + By = C

*A, B, C cannot be fractions

*A cannot be negative

parallel lines

coplanar lines that do not intersect

same slope

different y-intercept

lines never touch

symbol → | |

perpendicular lines

2 lines that intersect to form right angles (always coplanar)

slopes are opposite signs and reciprocals

y-intercept can be same or different

symbol → ⊥

horizontal lines have slopes that are…

ZERO

• always written as y = #

  • where line crosses the y-axis

vertical lines have slopes that are…

UNDEFINED

• always written as x = #

  • where line crosses x-axis

points

• most basic building block of geometry

• no size, height, depth; only location (can be on a line, plane, or within space)

• represented with a dot

• named with a Capital letter

lines

• straight, continuous, infinitely many points

• infinite length in 2 directions, but no thickness

• represented by a line with arrows on the end

• named by placing a line symbol above the letters of 2 points on the line OR by a single, lowercase script letter

planes

• have only length and width, but no thickness

• can be described as a flat surface that extends infinitely along its length and width

• represented with a 4-sided figure that resembles a tilted piece of paper

  • BUT REMEMBER…INFINITE!

• named by using the word “plane” and 3 points on the plane (or a single script uppercase letter)

how many points “determine” a line?

2 DISTINCT points determine a line

how many points “determine” a plane?

3 DISTINCT NONCOLLINEAR points determine a plane

any 3 points are coplanar but not any 3 points determine a plane

a minimum of 3 points determine a plane, but 1 point MUST be collinear

collinear vs. non-collinear

on the same line

non: not on the same line

ANY TWO POINTS ARE COLLINEAR

coplanar vs. non-coplanar

on the same plane

non: NOT on the same plane

ANY 3 POINTS ARE COPLANAR

line segment

2 points called the ENDPOINTS of the segment and all the points between them that are collinear with the two points

• can be MEASURED.

• To denote: do not include the bar over the letters or use “m” for “measure” in front of the segment name.

rays

part of a line that begins at a point and extends infinitely in one direction

The 1st letter is the endpoint of the ray and the 2nd is any other point that the ray passes through

congruence

2 segments that have the same measure or length

symbol → ≅

congruent vs equal

congruent:

when using segment symbol (AB ≅ CD)

• pretend there is a segment symbol over it

equals:

no segment symbol (CP = AL)

numbers/measures (AL = 7 cm)

addition, subtraction, multiplication, division (CP + AL = CL)

midpoint

the point on a segment that is the same distance from both endpoints

bisect

divide into 2 congruent parts

• the midpoint bisects the segment

space

the set of all points

what determines space? 4 DISTINCT COPLANAR points

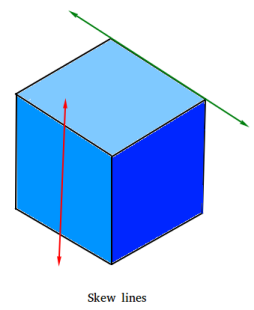
skew lines

non-coplanar lines that do not intersect

not contained (through) vs contains

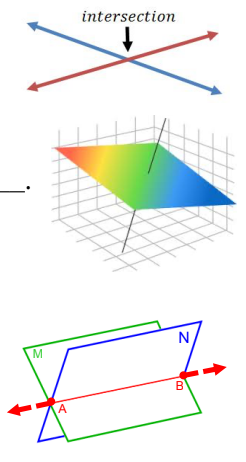
intersections

2 distinct lines intersect at a point

a plane and aline not contained in the plane intersect at a point

2 distinct planes intersect at a line

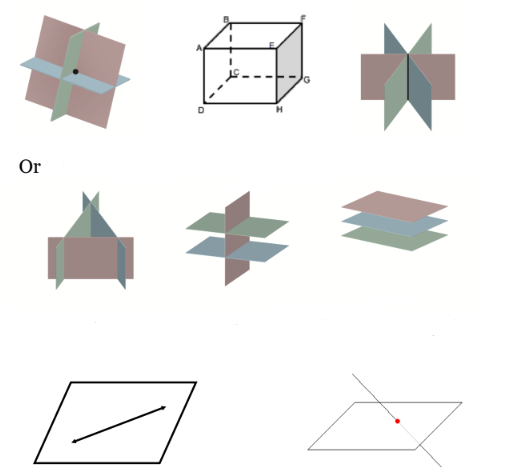
intersections (pt 2)

3 distinct planes can intersect at a line or a point

or no common point(s) of intersection

a line and a plane intersect at a point or infinite points

angle

formed by 2 rays that share a common endpoint

the common endpoint = VERTEX

the 2 rays = SIDES

symbol → ∠

naming angles (3 ways)

1) use 2 capital letters. VERTEX MUST BE MIDDLE LETTER (<TAP)
2) IFF (if and only if) an angle is alone, you may name it by its vertex only. (<A)

3) you can name an angle with a number if the angle is labeled with one (<1)

measure of an angle

measure of an angle is the smallest amount of rotation about the vertex from one ray to the other

• angles are measured in degrees

• to indicate the measure of <A we write m<A (m<A = 65 degrees)

reflex angle

the other “larger angle” with the same sides and vertex

• to find the reflex angle, we always subtract from 360 degrees

congruent angles + congruency statement + equality statement

congruent angles = angles with the same measure

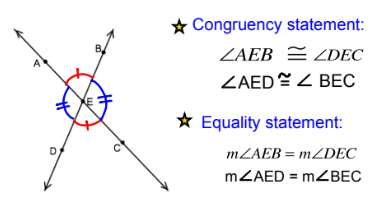
adjacent angles

• 2 coplanar

• non-overlapping

• common vertex

• one common side (next to each other)

angle bisector

a ray, line, or line segment that contains a vertex and divides an angle into 2 congruent angles.

if two triangles are similar then the lengths of corresponding angle bisectors are proportional to the lengths of corresponding sides

conditional statements

• If - then statements

• Usually written in two parts

• Hypothesis: The part of the statement that is known to be true/ the part after the if

• Conclusion: The part of the statement that can be concluded

Converse

a statement that reverses the hypothesis and conclusion

• Not always true

biconditional statements

combine original statement and the converse if they are both true

• Definitions are always biconditionals

• Can be written in reverse order

• Uses IFF (if and only if)

right angle

measures exactly 90 degrees

acute angle

measures less than 90 degrees but more than 0

obtuse angle

measures more than 90 degrees but less than 180 degrees

complementary angles

a pair of angles whose measures have a sum of 90 degrees

• do not have to be adjacent

supplementary angles

a pair of angles whose measures have a sum of 180 degrees

• do not have to be adjacent

vertical angles

angles formed by 2 intersecting lines that share a common vertex but not side

linear pair of angles

2 angles are a linear pair if they share a vertex and a common side and their noncommon sides form a line (adjacent angles that are supplementary)

straight angle

an angle whose measure is exactly 180 degrees/a straight line

3rd side rule

The length of any side of a triangle must be greater than the difference of the other 2 sides and less than the sum of the other 2 sides (when asked to list all sides: difference < 3rd side< sum)

3rd angle rule

If two angles are congruent the third angle is also congruent

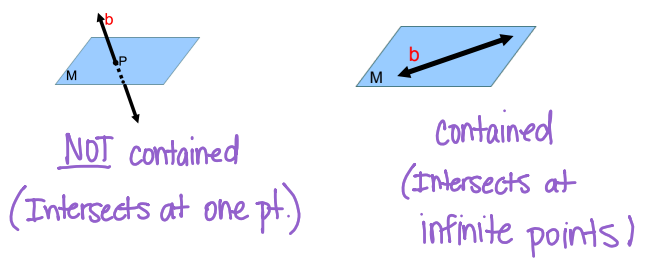
contained vs. not contained

contained: line intersects at infinite points

not contained: line intersects the plane at one point

midpoint formula

transversal

a line intersecting two or more other lines in a plane (red line in example)

corresponding angles

angles formed in corresponding positions (always on the same side of the transversal)

alternate interior/exterior angles

on alternate sides of the transversal on the interior/exterior of the 2 lines

same-side interior/exterior angles

same side of the transversal and on the interior/exterior of the two lines

scalene triangle

has all different side measurements

equilateral triangle

has all the same side measurements

isosceles triangle

has at least 2 sides of the same length (all equilateral triangles are isosceles)

altitude

a segment from a vertex of a triangle perpendicular to the opposite side (or the line containing the opposite side)

if two triangles are similar then the lengths of corresponding altitudes are proportional to the lengths of corresponding sides

median

a segment from the vertex of a triangle to the midpoint of the opposite side

if two triangles are similar then the lengths of the corresponding medians are proportional to the lengths of the corresponding sides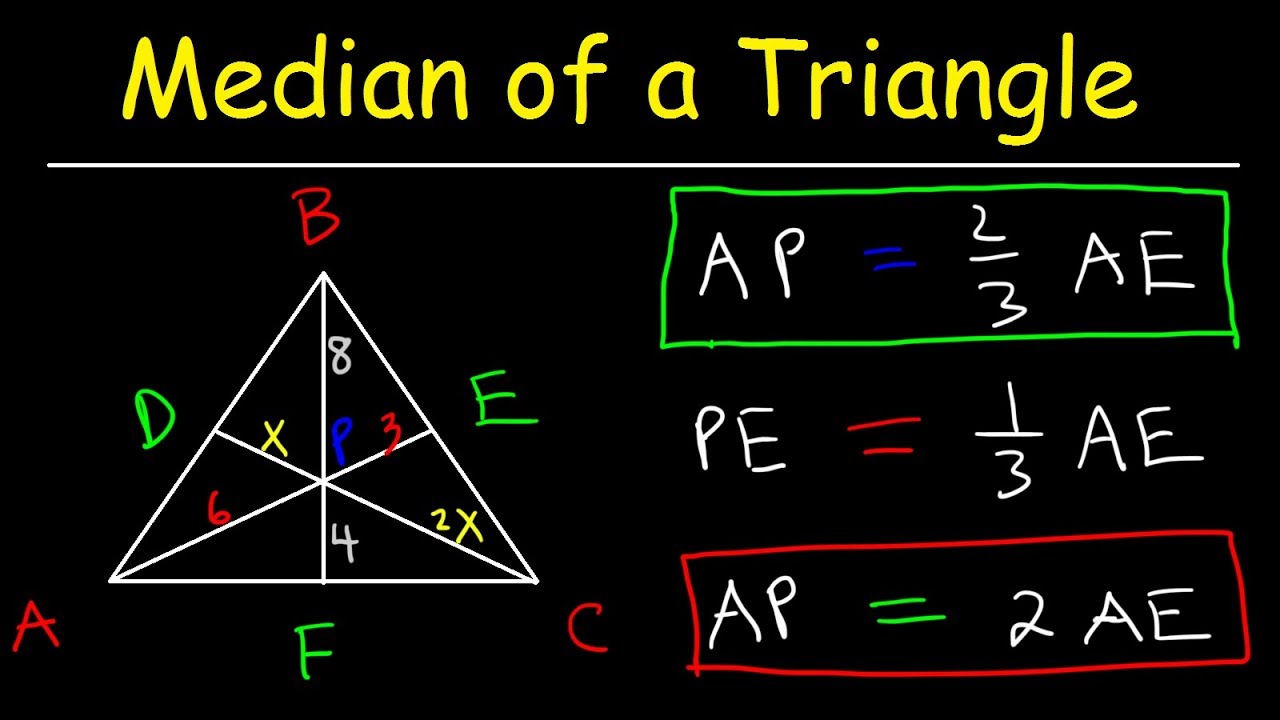

concurrent lines

a set of 3 or more coplanar lines that intersect at a point

POINT OF CONCURRENCY: where concurrent lines meet

centroid

a point of concurrency where the 3 medians intersect

• divides each median into 2 parts so that the distance from the centroid to the vertex is twice the distance from the centroid to the midpoint of the opposite side

• center of gravity

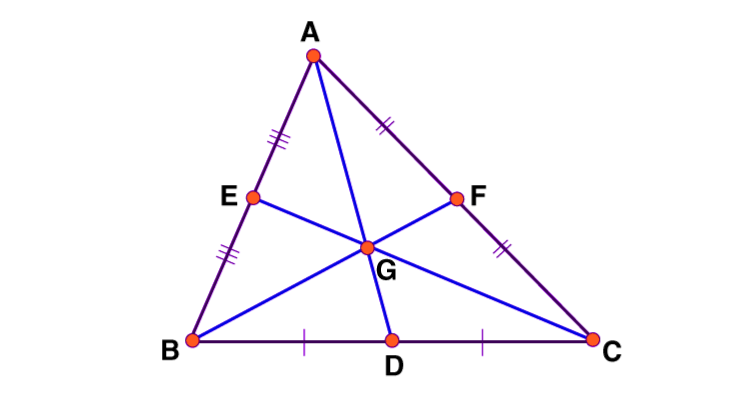
congruent triangles

triangles that have the same size and shape.

2 triangles are congruent if and only if all 3 pairs of corresponding angles and sides are congruent

similar figures

2 polygons are similar if their vertices can be paired so that'

• the corresponding angles are congruent

• the corresponding sides are all in the same proportion/ratio

similarity ratio + area ratio + volume ratio

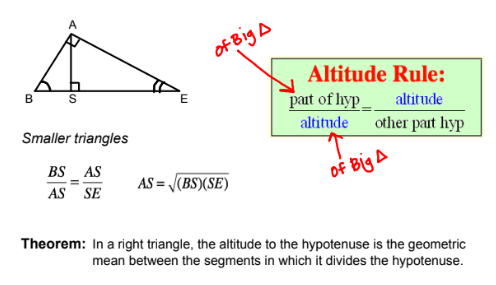
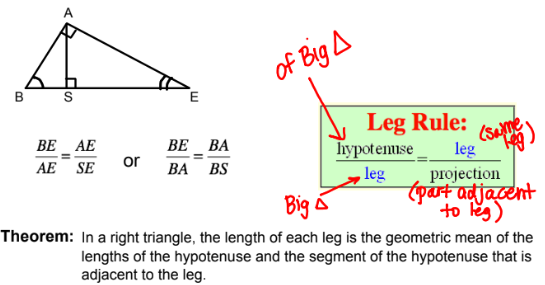
geometric mean

2 numbers are across from each other in a ratio

• in a geometric mean problem, the means are always the same values

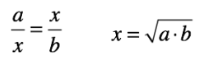
altitude rule

leg rule

translation

slides an object a fixed distance in a given direction

• Original shape and translation have the same shape and size (are congruent)

• Rigid transformation

• Facing same direction/orientation

• Points that are collinear stay collinear

• Lines that are parallel in original are parallel in translation

• Midpoints of shape’s segments stay intact 

notation/rule for translations

<a,b>

(x,y) → (x+a, y+b)

T(a,b)

reflections

creates a congruent figure

• Isometric transformation (transformation that preserves length)

• Reflection is called a non-direct or opposite isometry

• Preserves:

  • Distance

  • Angle measures

  • Parallelism

  • Collinearity

  • Midpoint

reflection over x-axis

(x, -y)

reflection over y-axis

(-x, y)

reflection over y = x

(y, x)

reflection over y = -x

(-y, -x)

rotation

a transformation in which a figure is rotated about a fixed point

Center of rotation: the fixed point that the figure is rotated about

rotation 90 clockwise/270 counterclockwise

(y, -x)

rotation 180 clockwise/counterclockwise

(-x, -y)

rotation 90 counterclockwise/270 clockwise

(-y, x)

dilation

transformation that creates a similar figure

• Center of dilation: fixed point which terminates where the dilation is 

• K = scale factor or the ratio of the side length of the image to the corresponding side length of the pre-image

• Dilation is a reduction if 0<k<1 

• Dilation is a enlargement if k>1

dilation rule

(kx, ky)

composition

when two or more transformations are combined to form a new transformation

glide reflection

•  a transformation consisting of a translation combined with a reflection

  • Preserves:

    • Distance

    • Angle measures

    • Parallelism

    • Collinearity

    • Midpoint