Topic 5: Further mechanics and thermal physics

What does it mean for an object to be in uniform circular motion?

When an object is rotating at a steady rate

What is angular displacement? Formula?

the change in the angle as an object rotates

2π/T, or 2πf

also: v/r (where r = the radius of the circle for like centripetal stuff)

What is ω?

angular velocity or angular frequency

What is centripetal acceleration?

The acceleration that occurs in circular motion

What is centripetal force?

a force that acts on a body moving in a circular path and is directed toward the centre around which the body is moving.

What is the formula for centripetal force?

F = mv^2/r

or F = mω^2r

What is the formula for centripetal for a car driving over a hill at top of the hill?

S -mg = mv^2/r

Where S = the support force (normal reaction) from the hill,

mg = weight

and mv^2/r = the centripetal force

On a roundabout, what provides the centripetal force?

The friction

On a roundabout, what is the maximum fore for no slipping? (So the friction between the tyres and the road must be below a limiting value, F0, for this to occur)

F0 = mv0^2/ r

Where v0 = the max velocity at which this can occur.

For a banked track, what is the formula for the velocity at which there is no sideways friction?

v^2 = grtanθ

Where θ is the angle of the track to the horizontal

What is the formula for phase difference in radians?

2π.Δt/T

What are the units for angular frequency?

rad s^-1

What are the two conditions needed for shm?

acceleration is always in the opposite direction to the displacement

acceleration is proportional to the displacement

How can you reduce the frequency of the oscillations of a mass on a string? Why does that work?

add extra mass (increases inertia)

use weaker springs (reduces restoring force at any given displacement so acceleration and speed also reduces)

For a mass on a spring, what is the formula for restoring force?

-kx (k = spring constant, x = extension)

What is damping?

When the amplitude of an oscillating object decreases over time due to dissipative forces

Draw an energy-displacement graph for shm which includes GPE and KE.

(insert pic)

When does a system undergo forced vibrations?

When a periodic force is applied to a system

What is a periodic force?

Force applied at regular intervals

When is a system in resonance?

When the periodic force is in phase with the velocity of the oscillating system. Also, the phase difference between the displacement and the periodic force is π/2

What is the resonant frequency?

the frequency at the maximum amplitude.

When damping is lighter, what happens to resonance/ resonant frequency?

- the larger the maximum amplitude becomes at resonance

- the closer the resonant frequency is to the natural frequency of the system

For an oscillating system with little or no damping, at resonance, what is the applied frequency of the periodic force equal to?

the natural frequency of the system

What is Brownian motion?

random movement of particles; they change velocity and direction randomly

What causes Brownian motion?

Collisions between smoke molecules and the much smaller invisible air molecules

Use kinetic theory to explain why a gas in a container exerts a pressure on that container.

When a gas molecule collides with a wall, there is a change in direction, meaning there is a change in momentum. The wall exerts a force on all the particles, which is equal to the rate of change of momentum of all the particles. (Newton's second law: F = change in momentum/change in time)

The particles exert an equal and opposite force on the wall

the gas therefore exerts a pressure on the wall

Use kinetic theory to explain Boyle's law.

If the container's volume decreases, the particles hit the wall more frequently. The change in momentum remains the same, because the mean speed in unchanged at a constant temperature. But total force increases as the frequency does, so the pressure increases

Use kinetic theory to explain the pressure law.

If temperature increases, so does mean speed. So, change in momentum for each collision increases and so does the frequency of collisions. Therefore pressure increases with temperature.

Explain Charle's law using kinetic theory.

Temperature increases at constant pressyre so each collision has a greater change in momentum and therefore greater force. For pressure to remain constant, the volume of the container must increase since p=F/A.

What are the assumptions made in kinetic theory?

- the volume of the molecules is negligible compared to that of the gas

- the duration of each collision is negligible compared to the time between collisions

- forces between molecules are negligible

- all collisions are perfectly elastic

- the number of molecules in the gas is very large, so the laws of statistics apply

What is the formula for root mean square speed?

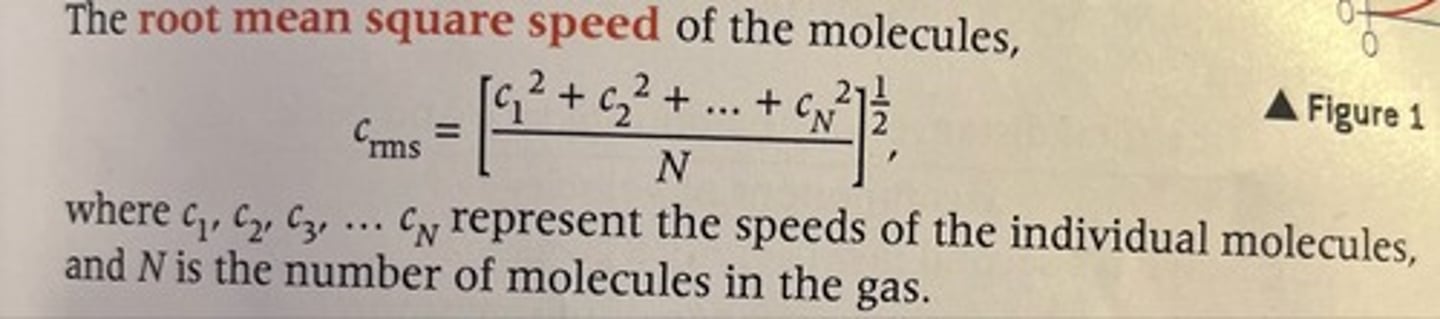
Derive the theory: pV = 1/3 Nm(Crms)^2

add picture

What do N and n stand for in thermal physics?

n = number of moles

N = number of molecules

What is Boyle's law?

for a fixed mass of gas at a constant temperature, pv = constant

What are isothermal changes?

changes that occur at a constant temperature

What is Charle's law?

for a fixed mass of gas at a constant pressure, the volume is directly proportional to the absolute temperature (temp in K)

What is an isobaric change?

a change at a constant pressure

What is the pressure law?

for a fixed mass of gas a constant volume, the pressure is directly proportional to the absolute temperature

What is the ideal gas law?

(pV)/T is constant for a fixed mass of an ideal gas.

it is equal to 8.31 for one mole of any ideal gas

Define internal energy.

The internal energy of an object is the energy of its molecules due to their individual movements and positions.

The internal energy of a system is the sum of the kinetic and potential energy of all the particles in the system.

How can the internal energy of a system be increased?

- heat the system

- do work on the system

What is the "triple point" of water?

the temperature at which ice, liquid water, and water vapor can coexist in contact with each other at thermodynamic equilibrium

What is 0K in celsius?

-273°C

Define specific heat capacity.

the energy required to raise the temperature of 1kg of a substance by 1K without a change in state

Define latent heat.

the energy required to change state of 1kg of a substance without a change in temperature.

Describe the conditions in which an experiment should be run so that gas tested will behave most like an ideal gas.

low pressure

temperature far above boiling point