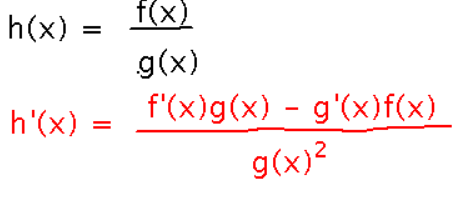AP Calculus AB Flashcards

Pythagorean Identity #1

sin²θ + cos²θ = 1

Pythagorean Identity #2 (divide by sin²)

1 + cot²θ = csc²θ

Pythagorean Identity #3 (divide by cos²)

tan²θ + 1 = sec²θ

Double Angle Identity #1

sin2θ = 2sinθcosθ

Double Angle Identity #2

cos2θ = cos²θ - sin²θ = 2cos²θ - 1 = 1 - 2sin²θ

Double Angle Identity #3

tan2θ = 2tanθ/1 - tan²θ

lne = ?

1

ln 1 = ?

0

log 10 = ?

1

log 1 = ?

0

log_nn = ?

1

log_n1 = ?

0

logA^B = ?

BlogA

log (A ⋅ B) = ?

logA + logB

(x,y) in terms of cos and sin

(cosθ, sinθ)

tan = ?

sinθ/cosθ

cotθ = ?

cosθ/sinθ

IVT

if a function is continuous on [a, b], and if k is any number between f(a) and f(b), then there must be a value in [a,b] such that f = k

end points aren’t equal, closed interval, continuous

definition of derivatives

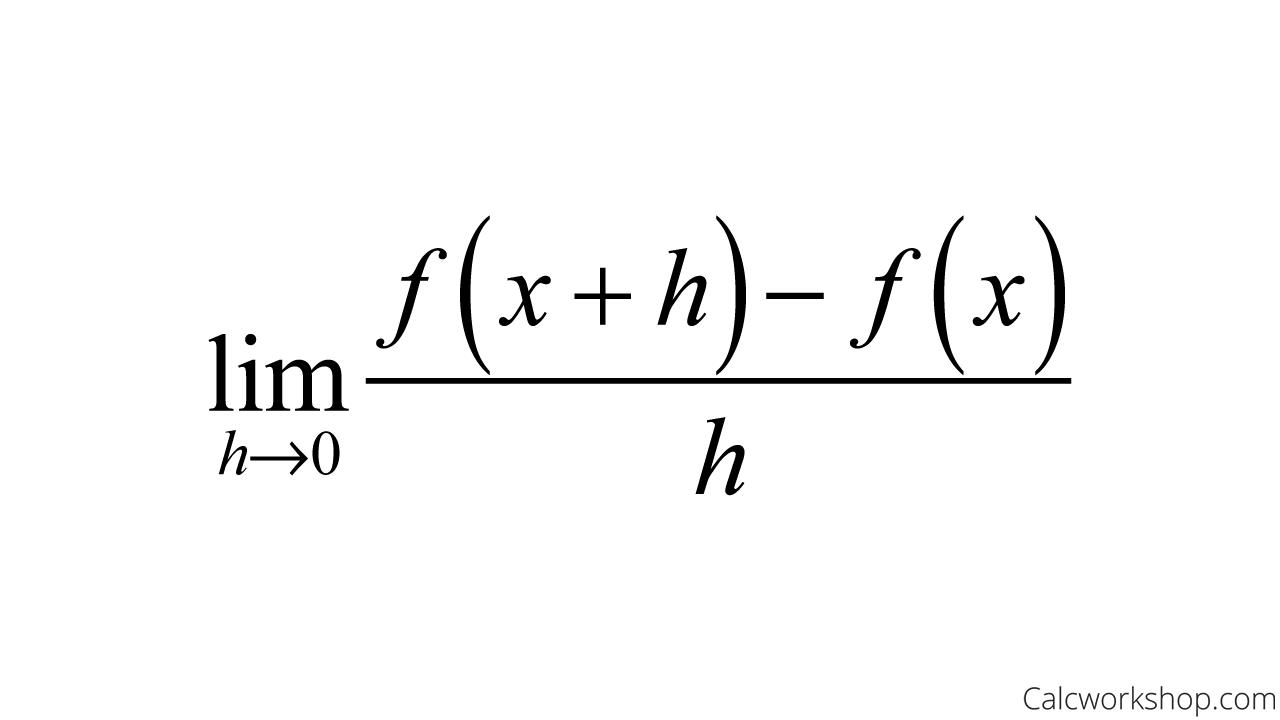
point slope formula

y-y1 = m(x-x1)

d/dx

derivative

d/dx axⁿ

a * nx^n-1

d/dx sinx

cosx

d/dx secx

secx * tanx

d/dx a (a is a constant)

0

d/dx cosx

-sinx

d/dx cscx

-cscx * cotx

d/dx cotx

-csc²x

d/dx tanx

sec²x

d/dx lnx

1/x

log_ex

lnx

d/dx log_ax

1/lna * x

d/dx e^x

e^x

d/dx a^x

lna * a^x

product rule

d/dx f(x) * s(x) = (f(x))(s^’(x)) + (f^’(x))(s(x))

f(x) = sinx * cosx

f^’(x) = cos2x

g(x) = cotx

g^’(x) = -csc²x

quotient rule