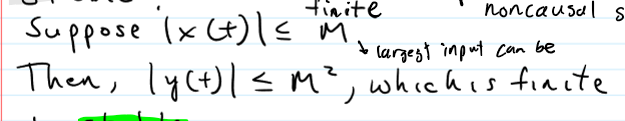Unit I - Intro to Biological Signals and Systems

Signal

physical quanity of interest; usually a function of time but can be of other variables (space or space + tiime); often used to mean the mathematical rep. of the physical qunatity

Image/Picture

a signal as a function of space; function of 2 spatial coordinates

Video

a signal as a function of time and space

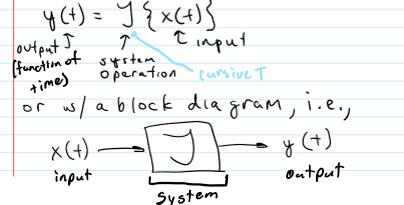
System

physical process that transforms 1 signal to another (input → output); can be denoted as an eqn. or a block diagram

What is this course about?

quantitative (mathematical) study of signals + systems of biological origins

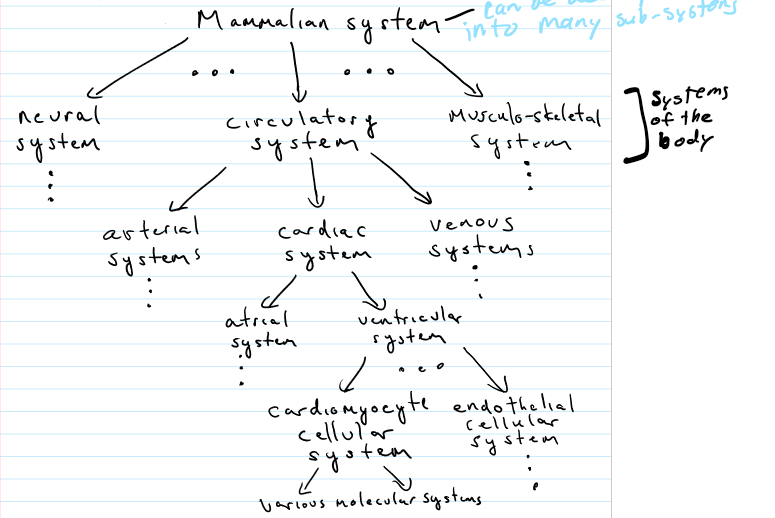
What can living systems be decomposed into?

many sub-systems’ meaning bio systems + their inputs and output signals are numerous/countless

Examples of Biological Signals

1. body temp. as a fcn of time (medical product)

2. V across a pair of electrodes on scalp as a fcn of time (EEG) (signals)

3. intra-cellular Ca conc. as a fcn of time (cellular)

4. knee joint angle as a fcn of time (mechanical)

5. x-ray image of inside boyd as a fcn of 2 spatial coordinates (signlas

Reasons for Quantitative Analysis of Biological Signals and Systems

1. extract info from signals to diagnose, monitor disease, anf guide therapy

2. model signals (put a fcn/eqn to it) to advance biological understanding and this conceive new tools to treat diseases

3 Classical Examples of Motivation to Study

1. automated arrythmia detection/analysis

2. speech coding

3. modeling auditory nerve fiber

Automated Arrythmia Detection/Analysis

normal heart rythm can be disturbed in the diseased heart which can result in limited blood flow = sudden death; ECG signal analysis commonly used

Arrythmia

irregular heart beat; can limit blood flow which can lead to sudden death; electric shock to chest to restore proper heart rhythm

ECG Signal Analysis

performed to detect arrythmias; saves lives

Speech Coding

helps with speaker recognition for the deaf and for security

Compressing Speech Signals to a Lower Bit Rate

important for transmitting and storing speech efficiently

Speech Signals

often modeled for speech coding

Time-Varying All-Pole Filter Model

resynthesize parameters and can hear w/o losing anything; pararmeters that reduce bit rate by a factor of 100

Modeling Auditory Nerve Factor

hearing is based on mechanical transduction so input signal (pressure wave a(t) = sound) and the output neural signal s(t) → higher brain centers (neural signal s(t)); system often subject of modeling

System Identification

standard modeling approach for sounds; rich input signal (a(t) or white noise) and output signal s(t) measured

White Noise

has all the frequencies to an equal extent

System Transfer Function (H(f))

determined from a(t) and s(t); w/ ^ means estimated this; can improve understanding of hearing/serves as basis for hearing aid designs for the deaf; if error small → eqn good for model

Signal Properties

1. continoues-time (CT) or discrete-time (DT)

2. deterministic or stochastic (random)

3. unidimensional or multidimensional

4. periodic or aperiodic

5. energy, power, or neither

Continous-time (CT)

signal defined for every instance of time

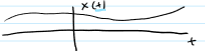
Discrete-time (DT)

signal defined at only certain instance of time (integras); specific points

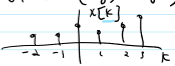
Deterministic

exact form of signal is known; ex. sinusoid

Stochastic (random)

only know statistics of signal; ex. noise

Unidimensional

function of only 1 independent variable; x(t)

Multidimensional

signal is a function of more than 1 independent variable; x(y.z); image or video processing

Periodic

signal repeats for all and some T (smallest T is the period); x(t) = x(t + T)

Aperiodic

signal is not periodic; doesn’t repeat

Biological Signals

CT, stochastic, uni- or multi-dimensional, and aperiodic (mostly)

Energy, Power, or Neither

signal can be thought of as a vector but w/ a continum of elements; convenient to represent it w/ a scalar value that indicates its size; if energy, can’t be power and vice versa (mutaully exclusive)

Average of Signal

not a good measure of signal size bc it doesn’t take the abs. value so - and + values cancel

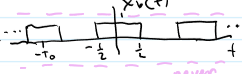
Power (Px)

average square of a signal; good measure of signal size; if x(t)’s power is non 0 but finite; has infinte energy

Energy (Ex)

sum of squares; good measure of signal size; if x(t) is non 0 but finite; has 0 power

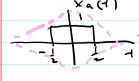
Rules of Thumb (sufficient conditions) to Classify Signals by Inspection

energy - must fit inside an exponential decay and not 0

power - must fit in a continous straight line (top and bottom) box thing; can’t be identically 0

neither - include x(t)=0 and signals that “blow up” (up and down) or grow in both time directions

Neither

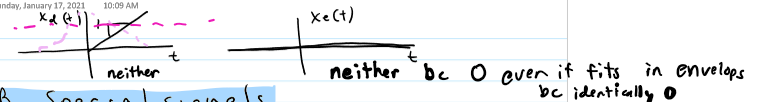
Special Signals

1. sinusoids and Euler’s relation

2. even/odd and even/odd parts of signals

3. exponentially-carying signal

4. singularity signals

5. impulse fcn (dirac delta fcn)

Sinusoids and Euler’s Relation

x(t) = Acos(wt + phi) = Acos(2*pi*f*t + phi)

A - amplitude

w - frequency (rad/s)

f - frequency (cycles/s)

phi - phase in rad

sin(x)

cos(x-pi/2)

cos(x)

sin(x+pi/2)

Euler’s Relation

e^(+-jx) = cos(x) +- jsin(x)

cos part is real

sin part is imaginary

cos(x) = ½ e^(jx) + ½ *e^(-jx)

sin(x) = 1/2j e^(jx) - 1/2j e^(-jx)

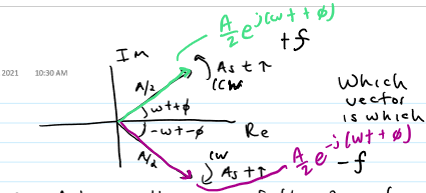
vectors rotate in opp. directions w/ angular frequencies of +- w rad/s

Positive Frequencies

means rate of ccw angular motion

Negative Frequencies

means rate of cq angular motion

Even/odd Signals

even x(t) = x(-t) and odd x(t) = -x(-t) for all time

most are neither but all real signsld can be express as the sum of even/odd parts

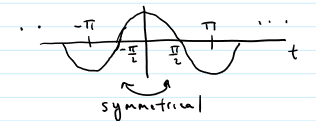
Even Signal

symmetrical about the y-axis; integral is double of half the time; ex. cos w/ 0 phase

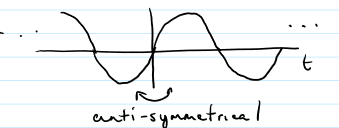
Odd Signal

anti-symmetrical about the y-axis (equal and opposite); integral is 0; ex. sin 2/ 0 phase

Neither Signal

even nor odd has neither symmetry

Rules to Classify Even/odd

X(even) + Y(even) = even

X(odd) + Y(odd) = odd

X(even) + Y(odd) = neither

X(even) * Y(even) = even

X(odd) * Y(odd) = even

X(even) * Y(odd) = odd

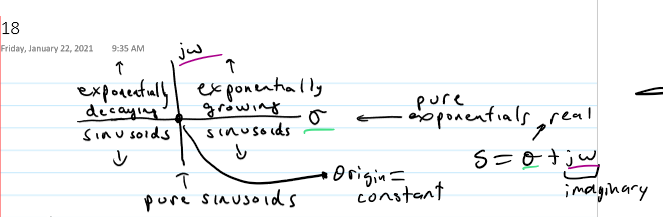
Exponentially-varying Sinusoids

x(t) = e^(st) where s = sigma + jw

x(t) = e^(sigma*t) e^(jwt) = e^(sigma*t) * (cos(wt) - jsin(wt))

S

complex freuqency

e^(st)

generalization of Euler’s relation/e^(jwt), where jw is generalized to a complex variable s = phi + jw

+- e^(sigma * t)

enveloped to an oscillating signal at frequency w

Special Cases of Expontentially-varying Sinisoid

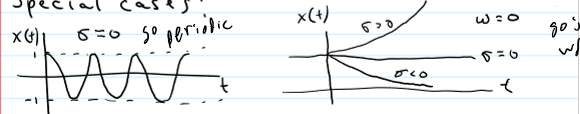
s-plane

for CT signals and systems

Singularity Signals

doesn’t have a derivative at 1 or more time instances

ex. ramp, steo, rectangular pulse, and triangular pulse

Ramp - Singularity Signal

no derivative at origin

Step - Singularity Signal

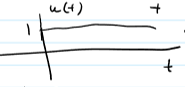
Ramp and Step Signals

useful for compactly writing signals w/ different mathematical descriptions over different time intervals

Rectangular Pulse - Singularity Signal

no derivative at 2 spots

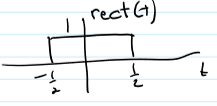
Triangular Pulse - Singularity Signal

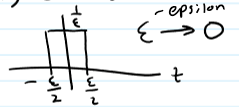
Impulse Function (dirac delta function)

2 important properties - multiplication and sifting

rectangular pulse w/ a height of 1/E and length of -E/2 → E/2

E → episilon

delta (t) - 0 for all t is not 0 and the integral from - infinity to + infinity is 1

Multiplication w/ Impulse Property

x(t)*delta(t) = x(0)*delta (t)

generalize → x(t)*delta(t-T) = x(T)*delta(t-T)

Sifting Property

address scenario where you multiply the impulse signal by another signal then integrate; intrgal of impulse = 1 so area under product of a signal w/ an impulse is the value of the signal at the location of the impulse

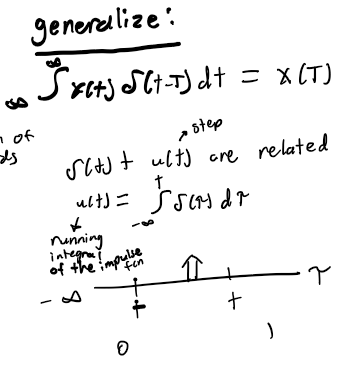
CT System Properties

1. linear or nonlinear

2. time-incariant or time-varying

3. casual or noncausal

4. dynamic or static

5. stable or unstable

Linear or Nonlinear

superposition principle; take 2 previous inputs, scale them by constants and then sum them (linear combination); a 0 input must yield a 0 outout for a system to be linear (if input multiplied by 0, output must be multiplied by 0)

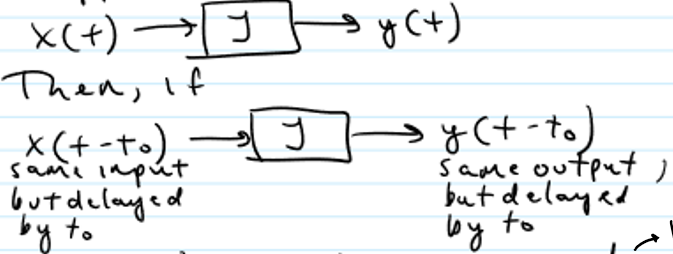
Time-invariant or time-varying

shape of input doesn’t depend on when input was applied

Causal or noncausal

causal - system response doesn’t depdns on future values of the input; present calue of output depends only on present and past values of input not future ones

Real world systems must be causal so why study noncausal?

independent variable of signaling not be time and non-real rime application (signal prerecorded or system is imolmented w/ a delay)

Dynamic or Static

static - output depends only on present value of input so thus memoryless

dynamic - has memory; output must depend on at least one oast or future valyu of input

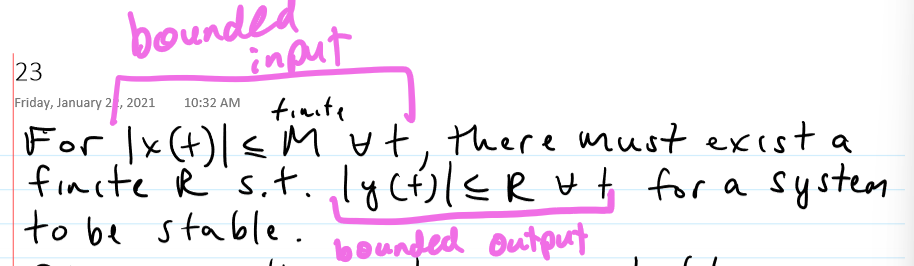
Stable or Unstable

stable - bounded input guarantees a bounded output (BIBO)

Linear Steps

1. replace x(t) w/ x1 and y(t) w/ y1

2. samething w/ x2 and y2

3. linear combination

linear if the output equals ax1(t) + by1(t)

Time-invariant Steps

1. find output to delayed input by to suppose input is g(t) = x(t-to) so y(t) = (g(t))² - (x(t-to))²

2. compute delayed output by substituting t w/ t-to in system eqn y(t-to) = x²(t-to)

3. if step 1 = step 2 then time-invariant

Casual Steps

present value of output depends only on present value of the input

Dynamic Steps

noncausal alwasy dynamic and static alwasy casual

Stable Steps