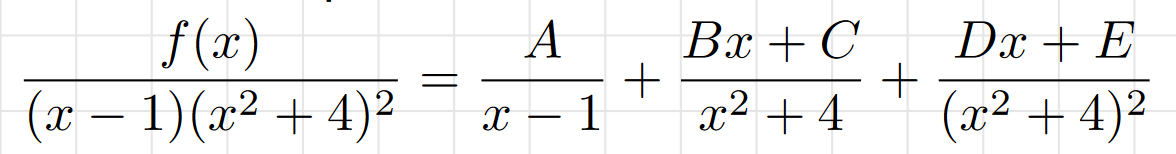Partial Fraction Decomposition

Rules of Decomposition

1. Use when we have a proper rational function. (Total degree of numerator is less than degree of denominator)

   -If not proper, no way to solve and therefore limit DNE

2. Denominator MUST be in factored form

3. Factors will come in two forms, linear or irreducible quadratic:

   -Linear: (x + 5), (2x - 1), x, etc

   -Irreducible Quadratic: x² + C

Goal: Split the rational function into multiple rational
functions that we can integrate, using a method we already
know

Steps for Decomposition

1. Determine the form of the partial fraction decomposition.
   Based on the denominator of the original rational function in FACTORED FORM. One fraction PER factor of the denominator

2. Determine the constants. This can be done either by solving a
   system of linear equations, or substituting values for x.

3. Carry out the integration.

Distinct Linear Factors

Each “x” is “distinct” and more easily separated into separate fractions

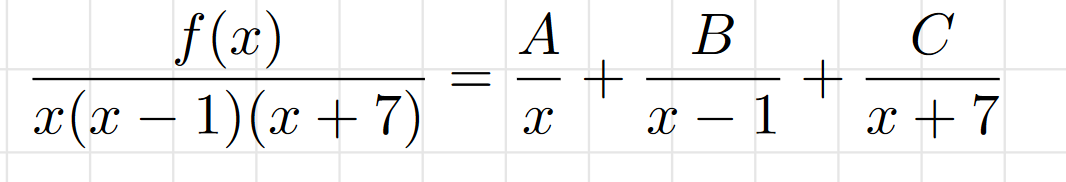
Repeated Linear Factors

Similar to “Distinct Linear Factors” however we now have exponents involved. Separate fractions need to be made for each “n” of the exponent

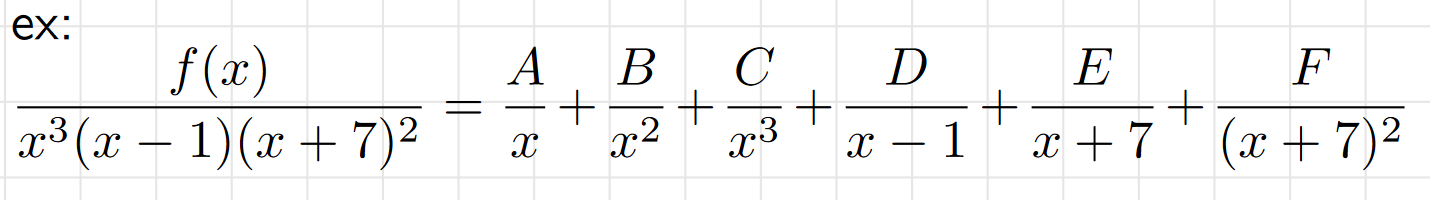
Distinct Irreducible Quadratic Factors

Similar to distinct linear, except the numerator has combined the AB, CD, etc

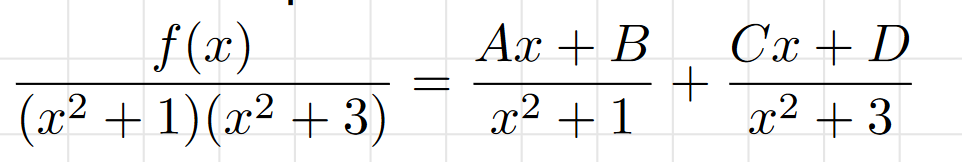
Repeated Irreducible Quadratic Factors

The most complicated, combines all the methods of distinct and repeated linear and distinct irreducible quadratic factors.