Lesson 3.3 Forces on an inclined plane

What is an inclined plane and why was it historically important?

A flat surface raised at one end used to raise or lower loads. Galileo used it to study uniformly accelerated motion because free-fall was too fast to measure with available timing devices.

How is the weight force resolved on an inclined plane? State the two components.

Weight (Fᵍ = mg) resolves into: Parallel component: Fₚ = mg sin θ (causes motion down the plane). Perpendicular component: F⊥ = mg cos θ (balanced by normal force).

Why does the normal force on an inclined plane equal mg cos θ?

The normal force (Fₙ) equals the perpendicular component of weight because there is no acceleration perpendicular to the plane. Since net force perpendicular is zero: Fₙ = F⊥ = mg cos θ

For a frictionless incline with no other forces what is the acceleration formula and why is mass irrelevant?

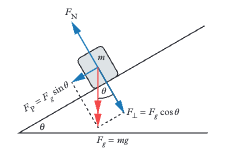
a = g sin θ. Mass cancels because Fₙₑₜ = ma and Fₚ = mg sin θ gives ma = mg sin θ so a = g sin θ. Acceleration depends only on angle not mass.

On an incline with friction what determines whether an object accelerates or moves at constant speed?

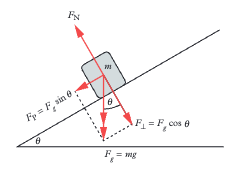
If Fₚ > Fᶠ: object accelerates down. If Fₚ = Fᶠ: object stays stationary OR moves at constant speed (zero acceleration does not mean zero velocity). If Fₚ < Fᶠ: object remains stationary.

For an object being pulled UP a frictionless incline by tension what is the condition for constant velocity?

Constant velocity means zero net force so tension equals the parallel weight component: Fₜ = Fₚ = mg sin θ. If Fₜ > Fₚ the object accelerates up the incline.

In a pulley system with a block on an incline and a hanging mass what determines the direction of motion?

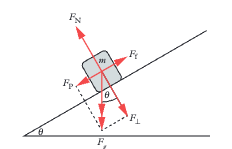
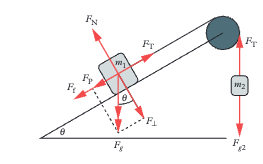
Compare tension (Fₜ = weight of hanging mass = m₂g) with parallel component (Fₚ = m₁g sin θ). If Fₜ > Fₚ: block accelerates up. If Fₜ = Fₚ: stationary or constant speed. If Fₜ < Fₚ: block accelerates down.

What happens to the parallel and perpendicular weight components as the angle of elevation increases?

As θ increases: sin θ increases so Fₚ = mg sin θ increases (more force down the plane). cos θ decreases so F⊥ = mg cos θ decreases (less normal force). At 90° Fₚ = mg and F⊥ = 0 (free fall).

When an object is pulled UP an incline WITH friction acting what forces act down the plane?

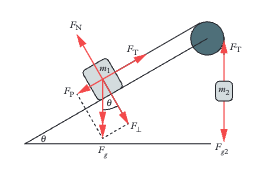
Both the parallel weight component (Fₚ = mg sin θ) AND friction (Fᶠ) act down the plane opposing the motion. Net force equation: Fₙₑₜ = Fₜ - Fₚ - Fᶠ.

What is the key study tip for remembering the weight components on an incline?

Fₚ = mg sin θ (parallel - "sin" for sliding). F⊥ = mg cos θ (perpendicular). These are NOT in the QCAA formula book so must be memorised. As θ increases sin θ increases and cos θ decreases.

A 20 kg object rests on a 30° incline. Calculate: (a) parallel component of weight (b) perpendicular component (c) normal force.

(a) Fₚ = mg sin θ = 20 × 9.8 × sin 30° = 20 × 9.8 × 0.5 = 98 N down the plane. (b) F⊥ = mg cos θ = 20 × 9.8 × cos 30° = 20 × 9.8 × 0.866 = 170 N (2 s.f.). (c) Normal force Fₙ = F⊥ = 170 N perpendicular to surface