[3MI101] Procvičování k ústní zkoušce (mikro+makro)

~~~work in progress~~~ Procvičování ke zkoušce z předmětu 3MI101 (Ekonomie 1) na VŠE. ~~~ Vychází z poznámek: https://bit.ly/3mi101-otazky ~~~

Užitek

Subjektivní pocit uspokojení plynoucí ze spotřeby jednotlivých statků

Graf užitku

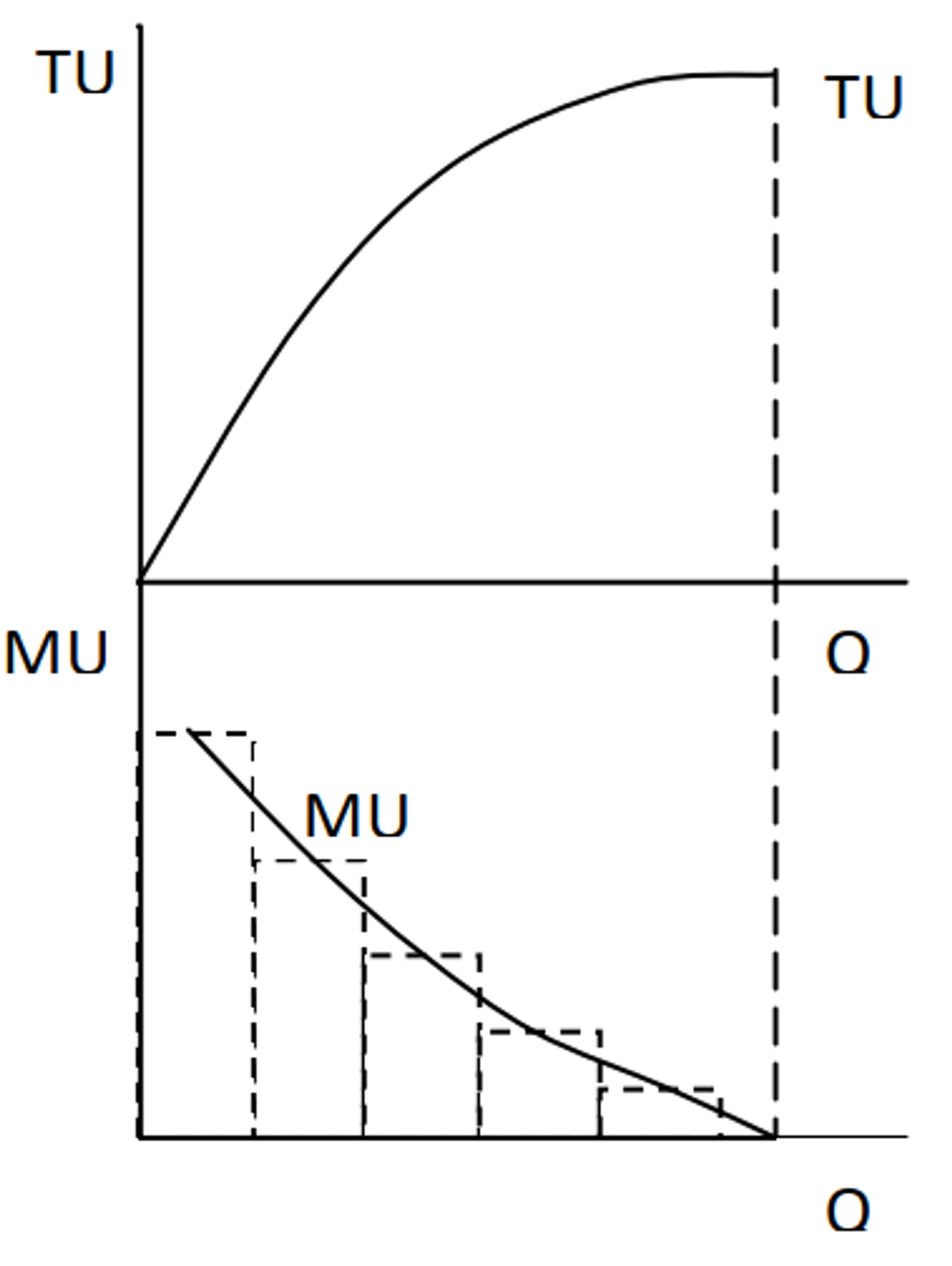
Výpočet mezního užitku

MU = \frac{\Delta TU}{\Delta Q}

Zákon klesajícího mezního užitku

S každou další jednotkou statku MU klesá

Optimum spotřebitele v kardinalistické teorii

P=MU → maximální možný užitek

Zákon rovnosti mezního užitku

\frac{MU \, \text{statku 1}}{P \, \text{statku 1}} = \frac{MU \, \text{statku 2}}{P \, \text{statku 2}} = \frac{MU \, \text{statku 3}}{P \, \text{statku 3}}

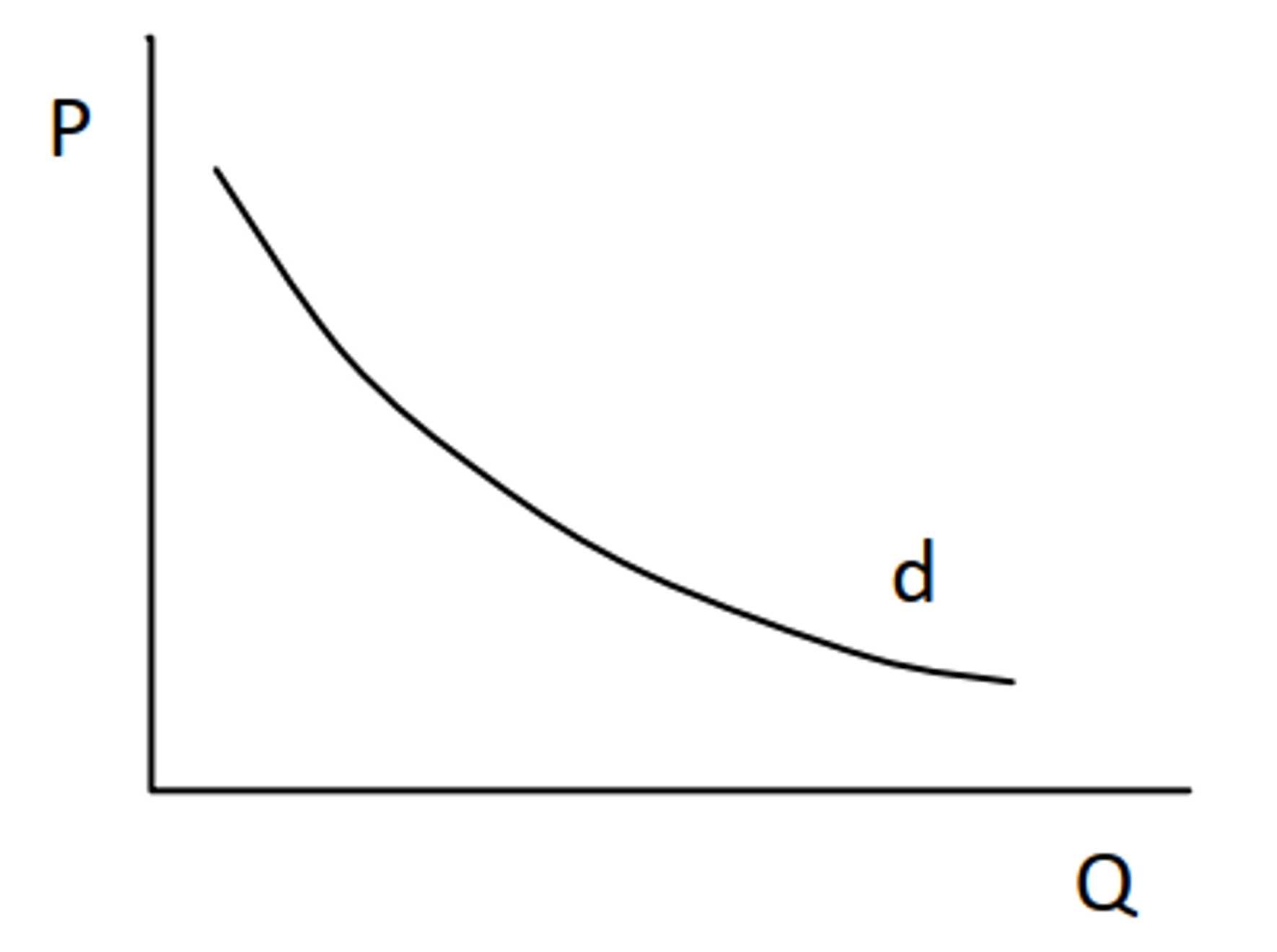
Odvození křivky poptávky z křivky užitku (kardinalistická teorie)

Křivka individuální poptávky je totožná s křivkou mezního užitku

Ordinalistická teorie užitku

Užitek je neměřitelný

Spotřebitel porovnává užitek různých kombinací statků ⇒ indiferenční křivky a indiferenční mapy

Kardinalistická teorie užitku

Předpokládá, že užitek je měřitelný

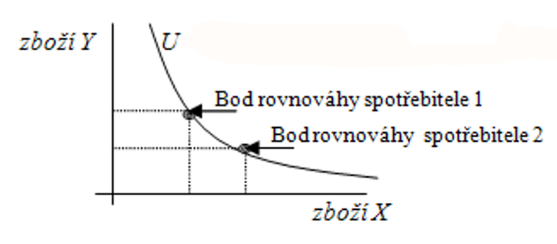
Indiferenční křivka

= znázorňuje kombinace množství dvou statků, které poskytují spotřebiteli stejný užitek

• Čím více statku X, tím méně statku Y

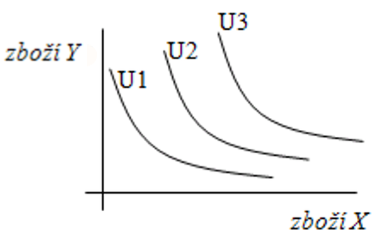
Indiferenční mapa

Soubor indiferenčních křivek

Mezní míra substituce

Poměr, v němž jsou statky nahrazovány:

MRS = \frac{\Delta Y}{\Delta X} = \frac{MU_x}{MU_Y}

Linie rozpočtu

I=P_X\cdot X+P_Y\cdot Y

Důchod = cena X množství X + cena Y množství Y

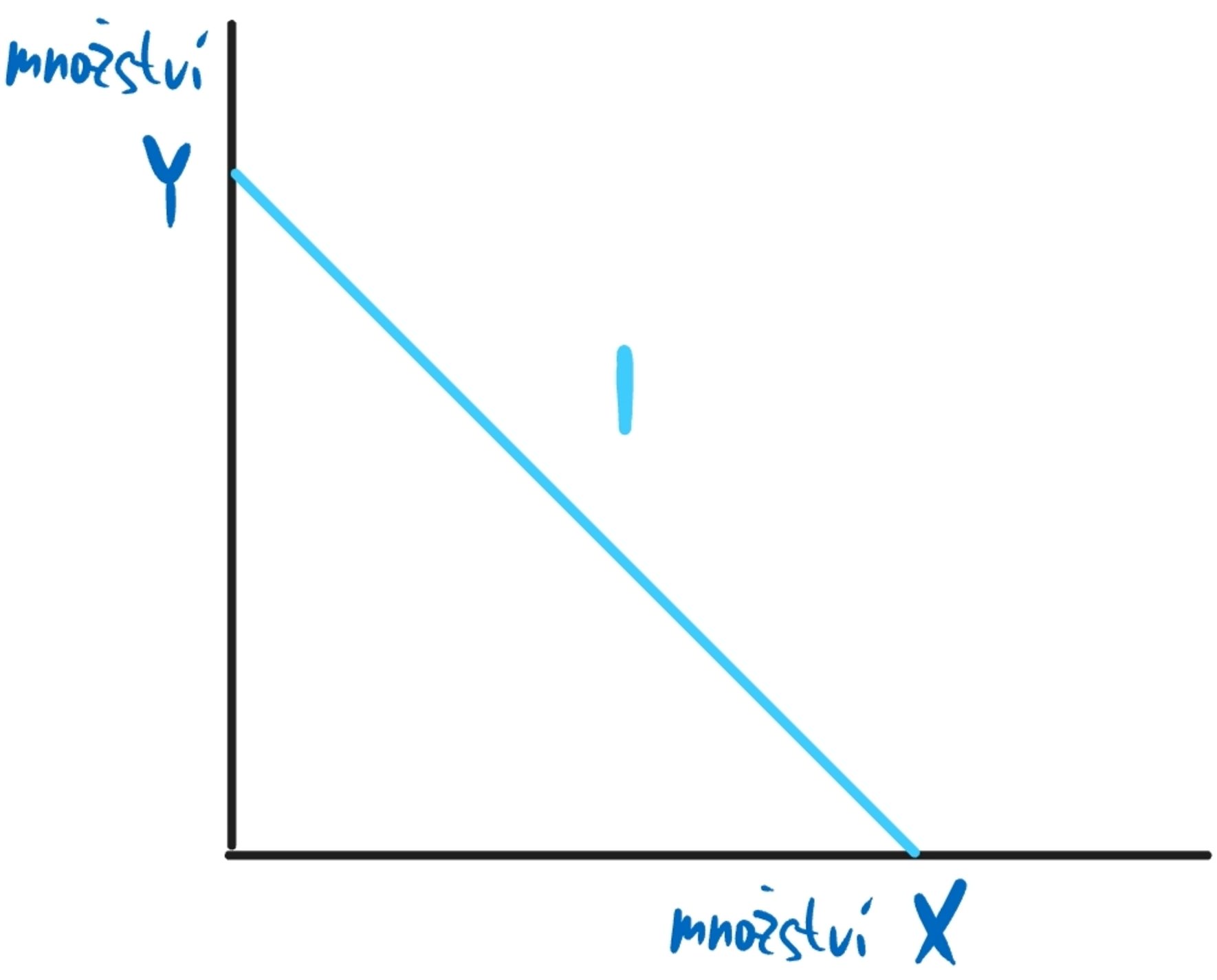
Optimum spotřebitele v ordinalistické teorii

V bodě, kde se linie rozpočtu dotýká indiferenční křivky

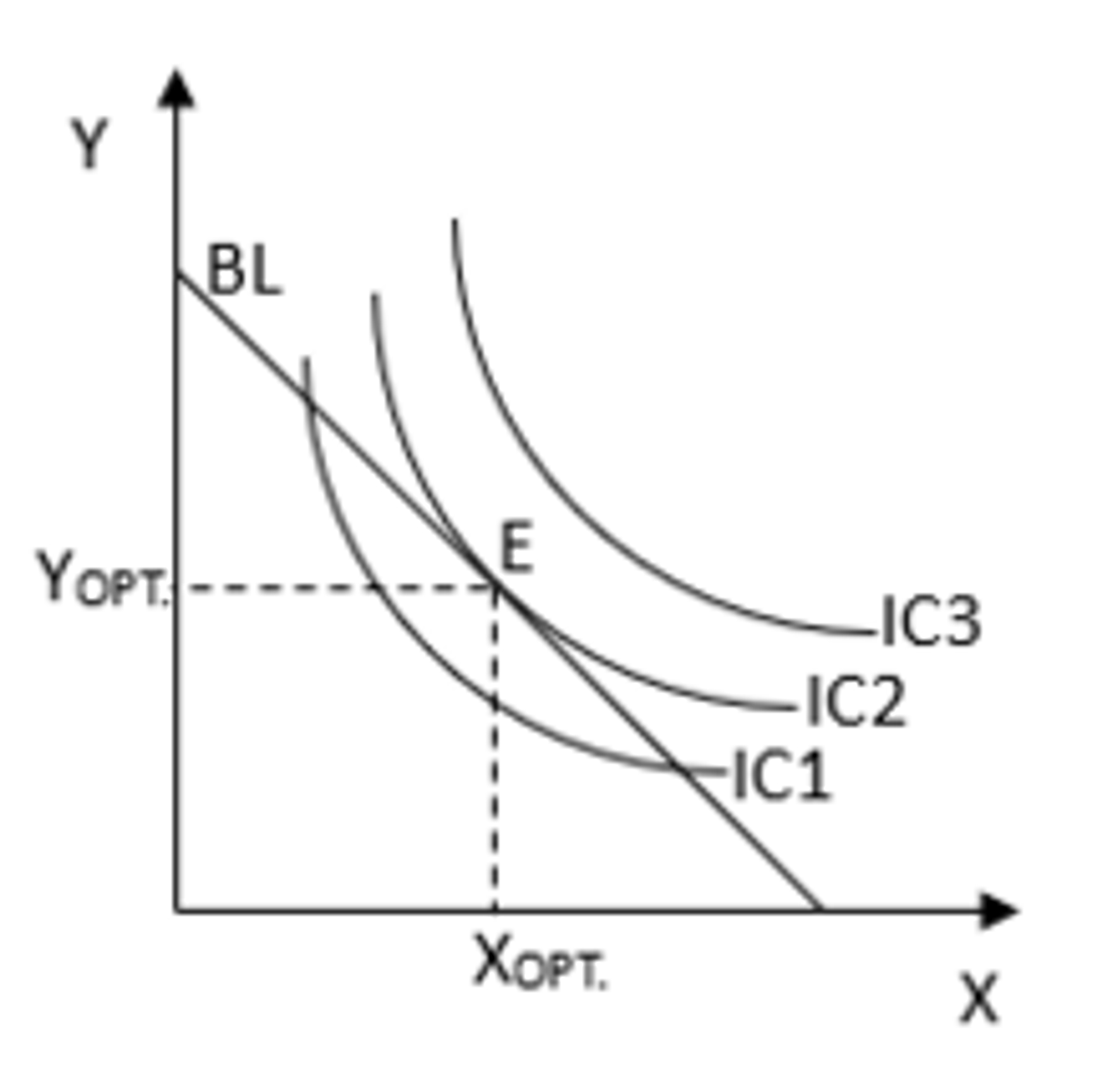
Odvození křivky poptávky z indiferenční křivky

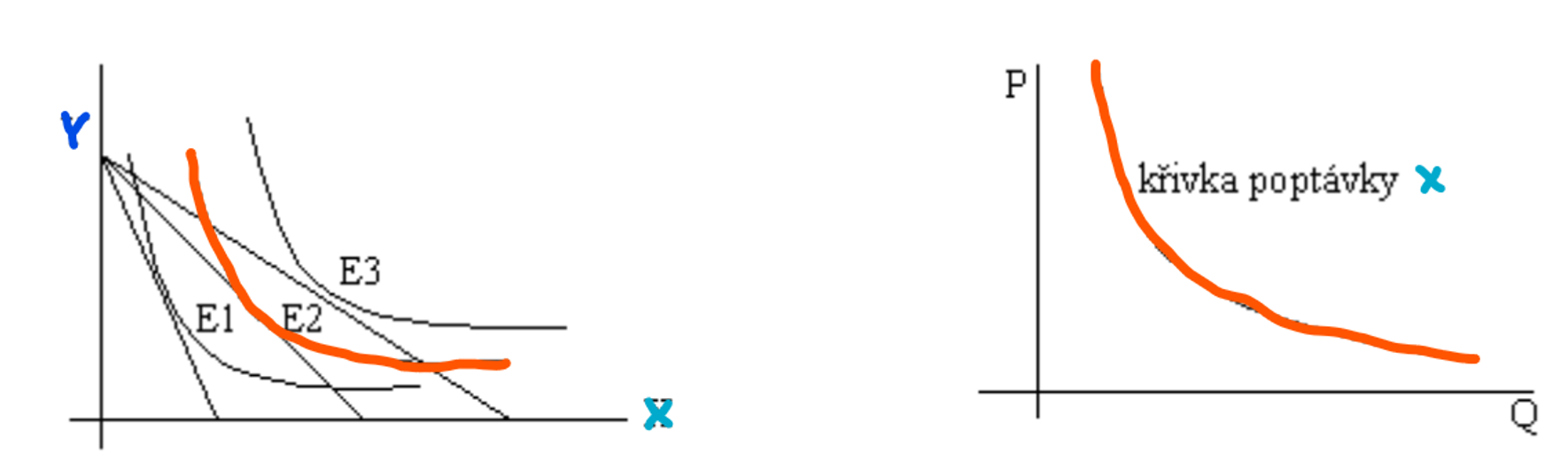
Faktory ovlivňující poptávku

• Substituční efekt

• Důchodový efekt

• Růst nominálního důchodu

• Změna preferencí spotřebitele

• Změny cen substitutů a komplementů

Substituční efekt

Pokud je cena jednoho statku příliš vysoká, vyměníme ho za jiný, levnější

Důchodový efekt

Při stejném důchodu a jedné ceně nakupujeme určité množství statku, pokud se cena změní, změní se i množství, které nakupujeme (důchod totiž zůstává stejný)

Dokonale elastická křivka

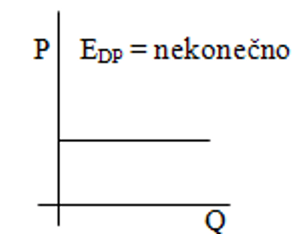
Dokonale neelastická křivka

Charakteristika krátkého období

Alespoň 1 fixní výrobní faktor (Půda, práce, kapitál)

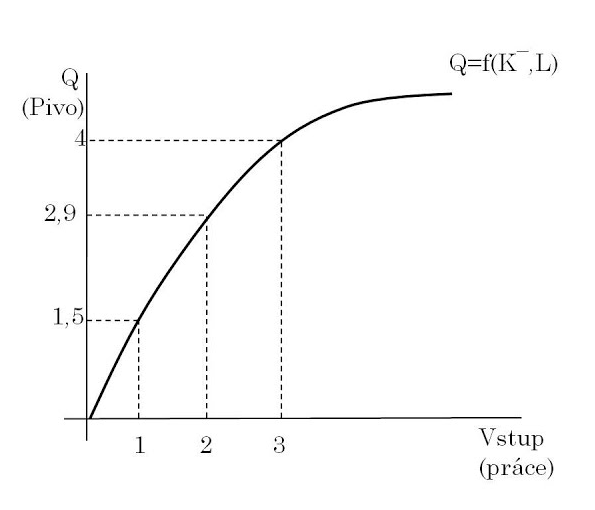
Produkční funkce v krátkém období (definice)

• Vyjadřuje maximální objem produkce, který je možno vyrobit danou kombinací výrobních faktorů při dané úrovni technologie

  Q = f (F_1, F_2, ... , F_n) ⇒ Q = objem produkce → kombinace výrobních faktorů

Celkový, mezní a průměrný produkt v krátkém období (graf)

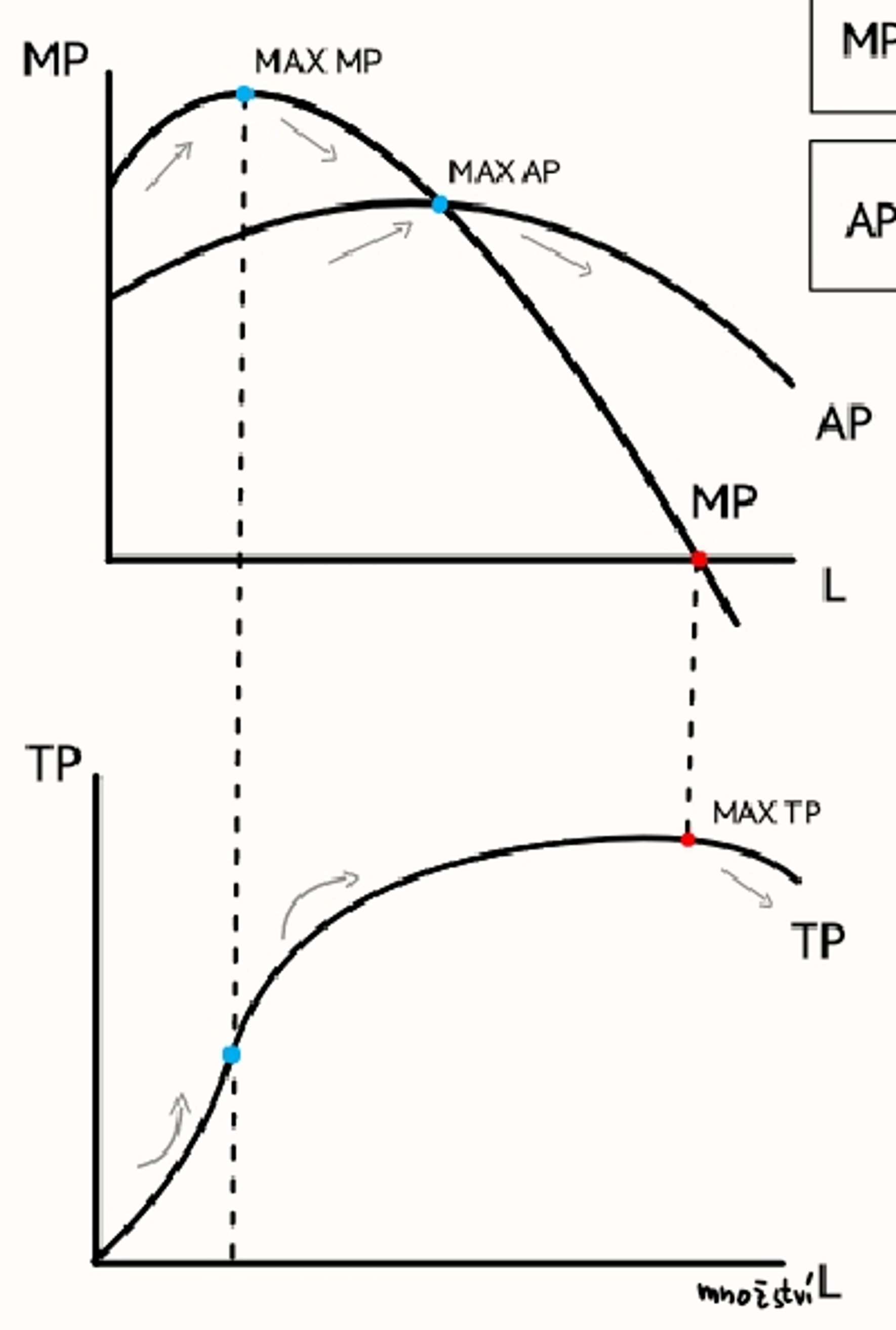
Celkový produkt (zkratka, definice)

TP ⇒ celkový objem produkce vyrobený určitým množstvím vstupu

Průměrný produkt (zkratka, definice, výpočet)

AP ⇒ objem produkce na jednotku vstupu

AP_F = \frac{TP}{F}

Mezní produkt (zkratka, definice, výpočet)

MP ⇒ změna produkce vyvolaná změnou množství vstupu o jednotku

MP_F = \frac{\Delta TP}{\Delta F}

Zákon klesajících mezních výnosů

S růstem množství jednoho vstupu se snižují přírůstky výstupu.

Nákladová funkce v krátkém období (graf)

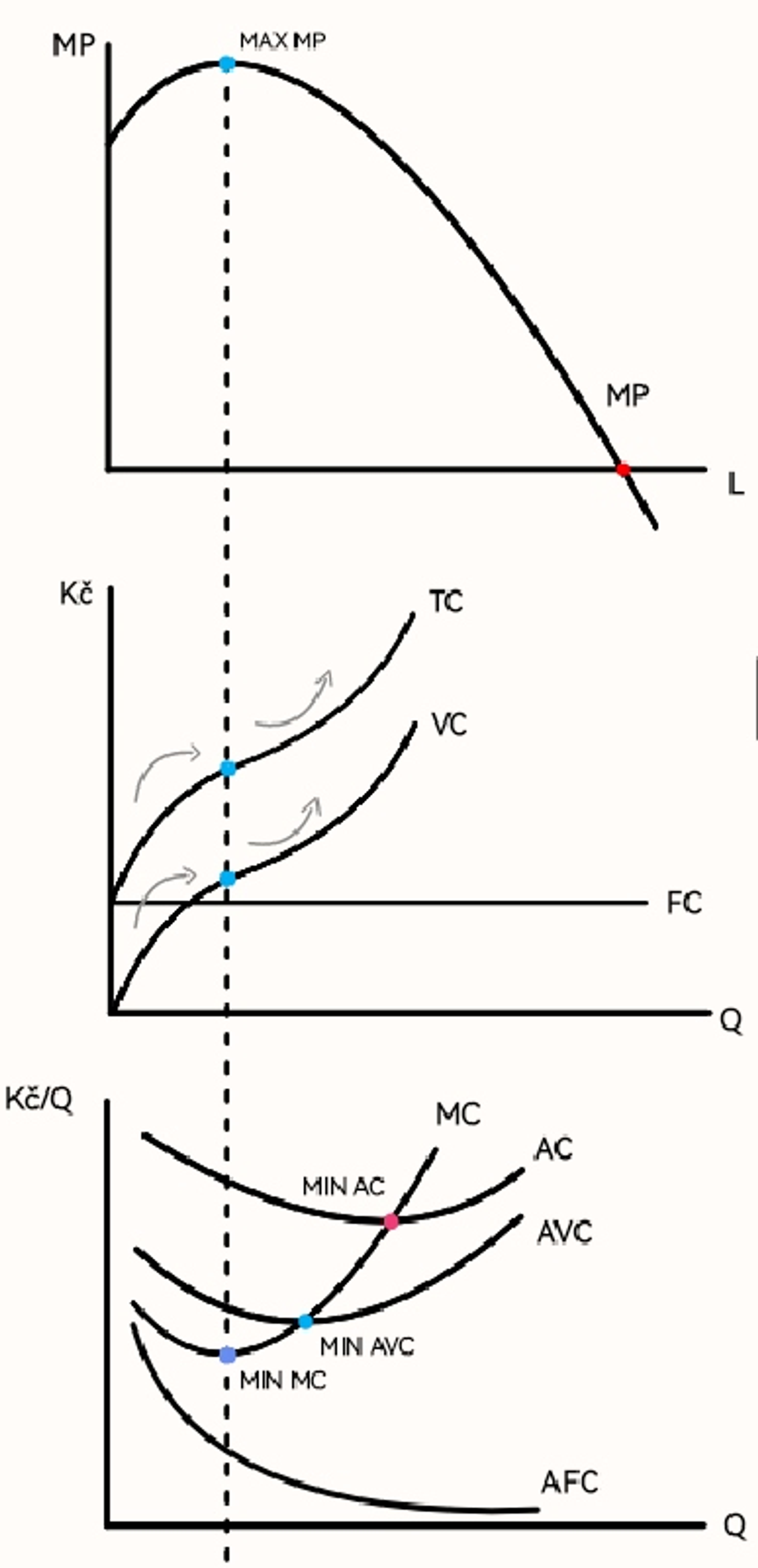
Fixní náklady (zkratka, definice)

FC ⇒ nemění se s objemem výroby → pořád stejn

Variabilní náklady (zkratka, definice)

VC ⇒ rostou s objemem produkce

Celkové náklady (zkratka, definice, výpočet)

TC ⇒ součet fixních a variabilních

TC = FC +VC

Průměrné náklady (zkratka, definice, výpočet)

AC ⇒ náklady na jednotku

AC = AFC + AVC = \frac{TC}{Q}

Mezní náklady (zkratka, definice, výpočet)

MC ⇒ náklady potřebné k rozšíření výroby o jednotku

MC = \frac{\Delta TC}{\Delta Q}

Odvození nákladové funkce z produkční funkce

Náklady závisejí na množství (je dáno produkční funkcí) a cenách vstupů

Dlouhé období (charakteristika)

Všechny vstupy (výrobní faktory) jsou variabilní

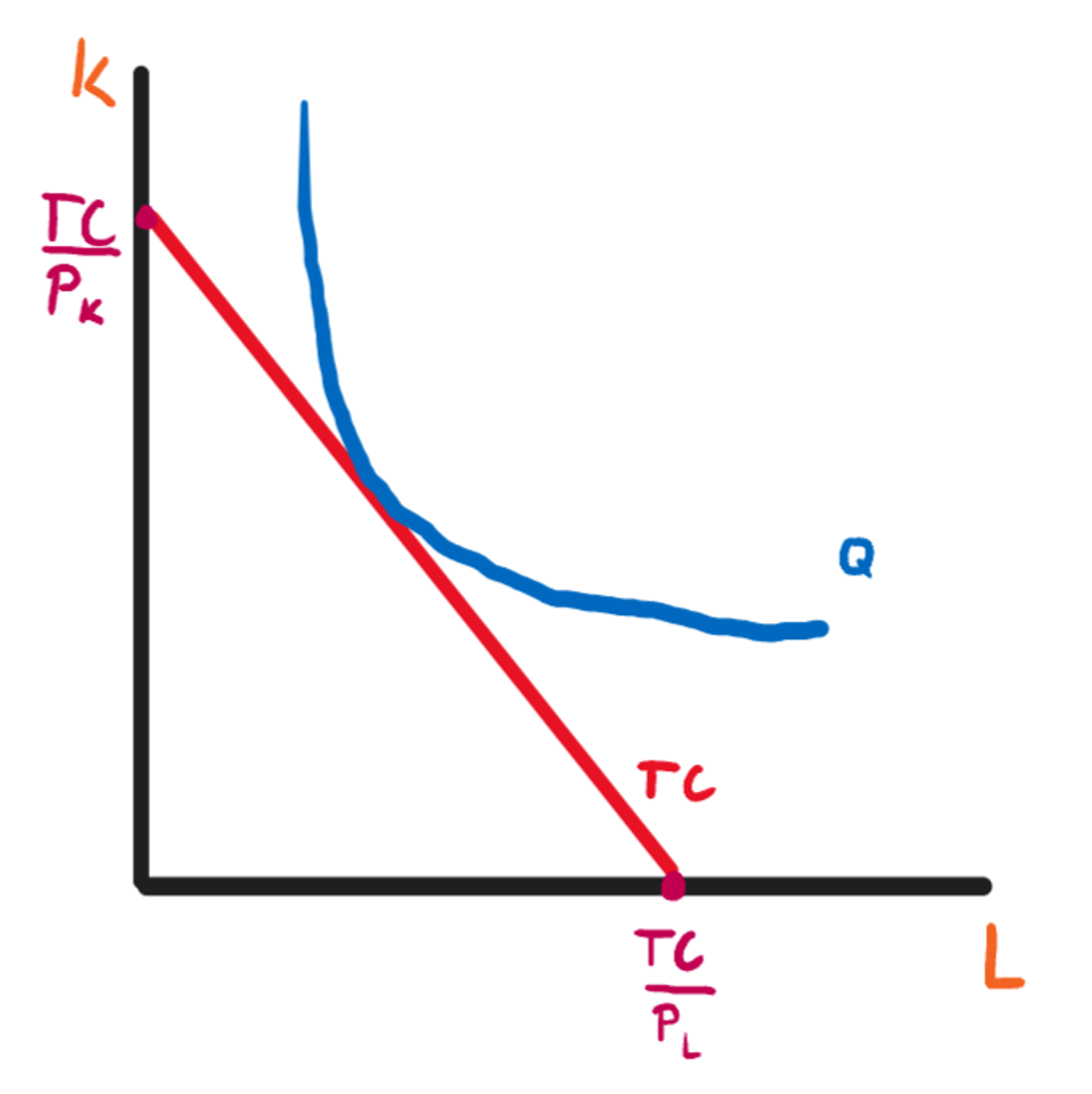
Izokvanta

Kombinace výrobních faktorů (kapitálu K, práce L), kterými vyrobíme stejný objem produkce

(Ta modrá křivka)

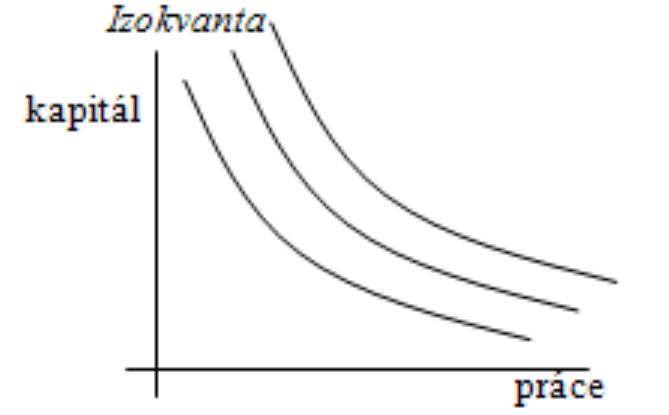
Mapa izokvant

Soubor izokvant

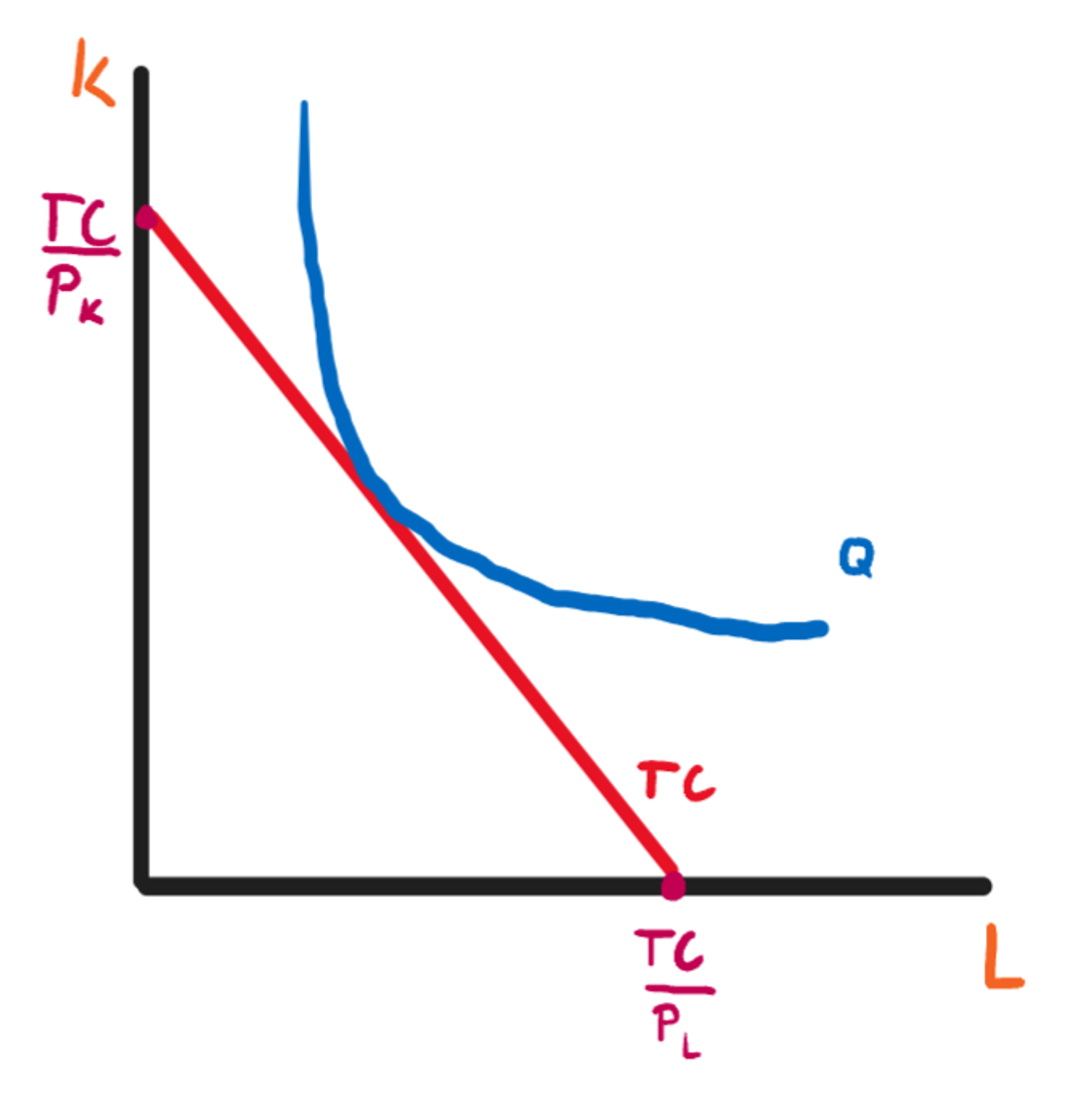
Izokosta

Kombinace výrobních faktorů v rámci stejných celkových nákladů

(Ta červená čára)

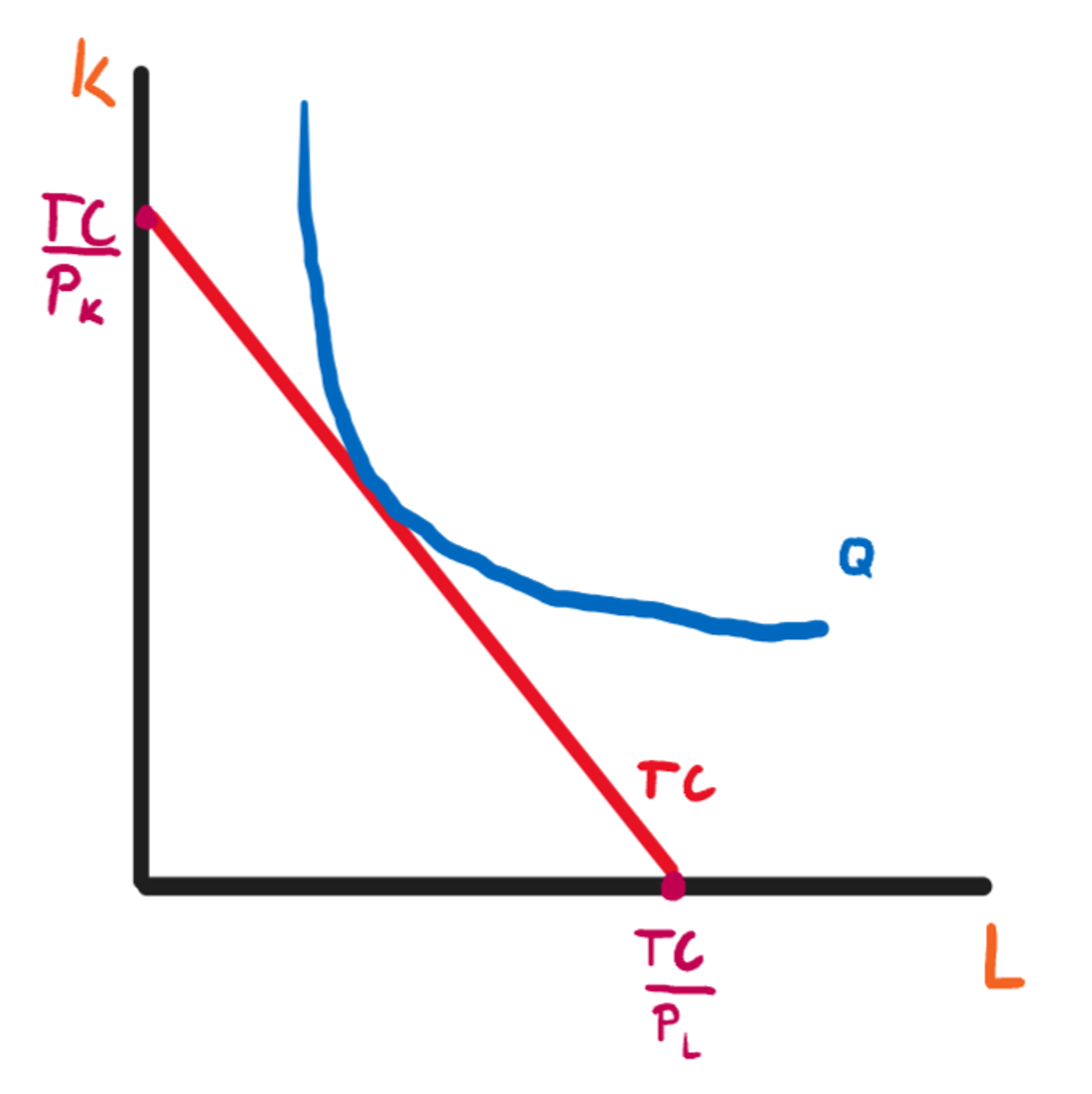
Nákladové optimum firmy

V bodě, kde se izokvanta dotýká izokosty

\frac{P_L}{P_K}=\frac{MPP_L}{MPP_K}

Odvození nákladové funkce z produkční funkce

• Různé linie celkových nákladů se dotýkají různých izokvant

• Každá další linie stejných celkových nákladů představuje vyšší náklady

• Zjistíme náklady odpovídající jednotlivým úrovním objemu výroby

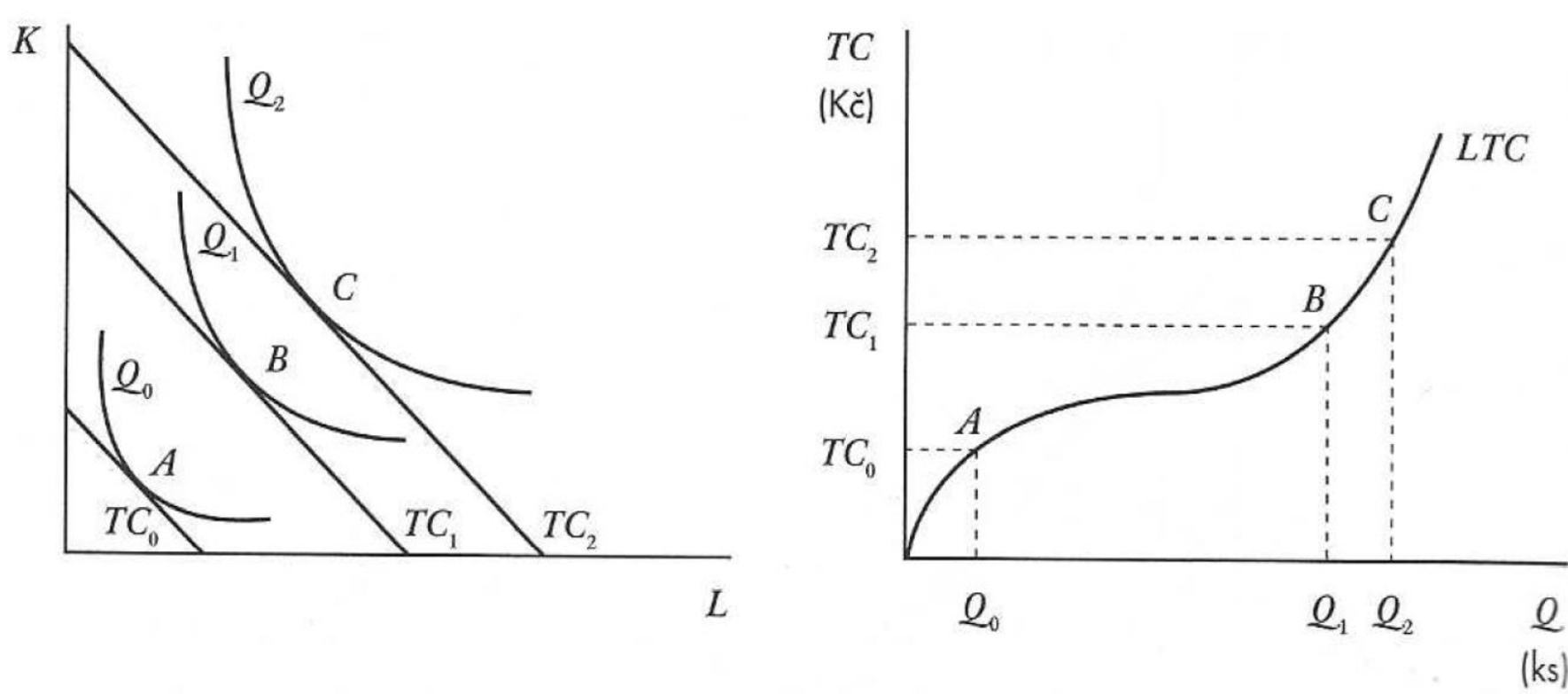
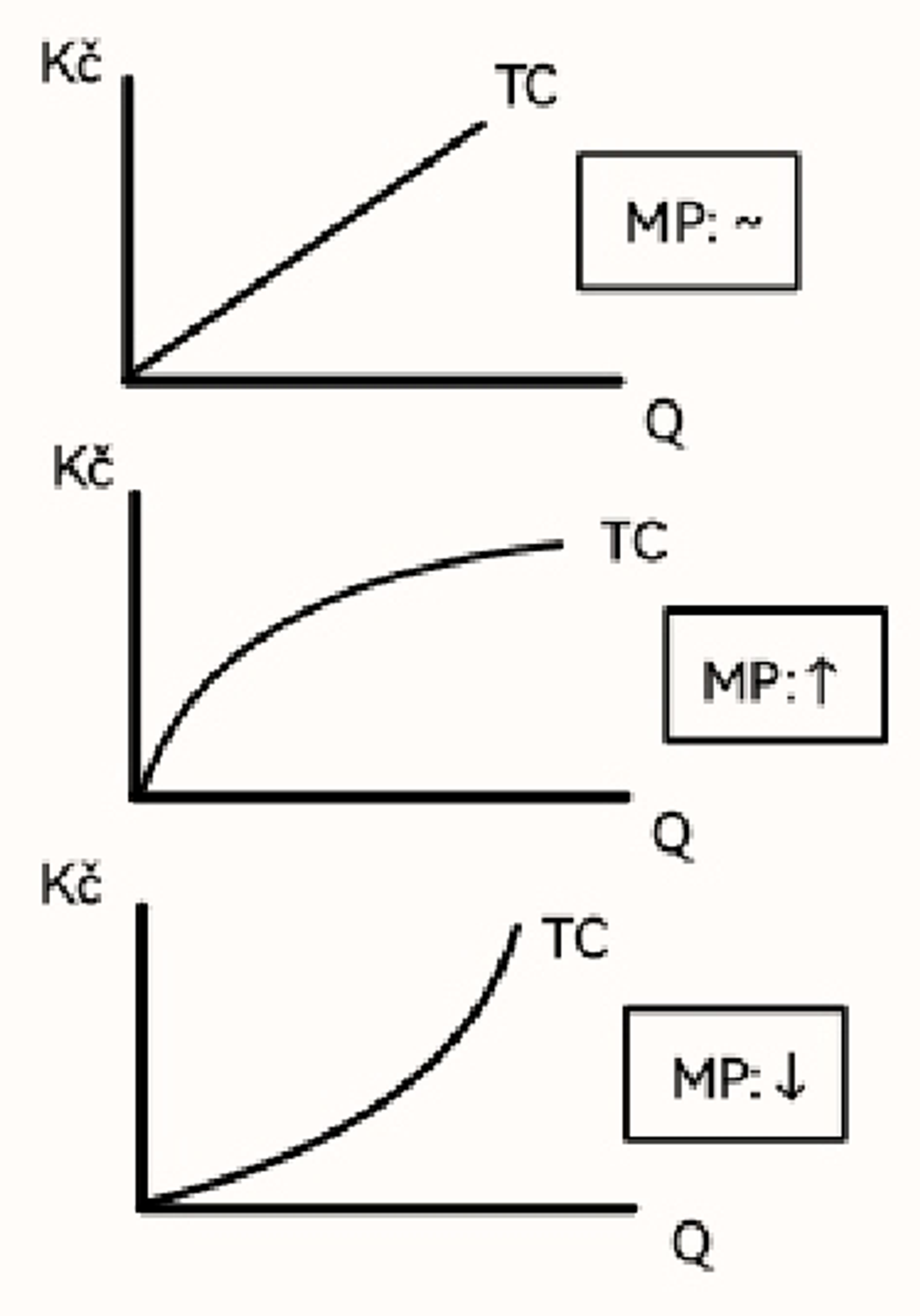
Výnosy z rozsahu (definice, typy, grafy)

= Změna výstupů v důsledku změny vstupů

• Rostoucí: 1% růst vstupu povede k růstu výstupu o více než 1 %

• Konstantní: 1% růst vstupu povede k růstu výstupu právě o 1 %

• Klesající: 1% růst vstupu povede k růstu výstupu o méně než 1 %

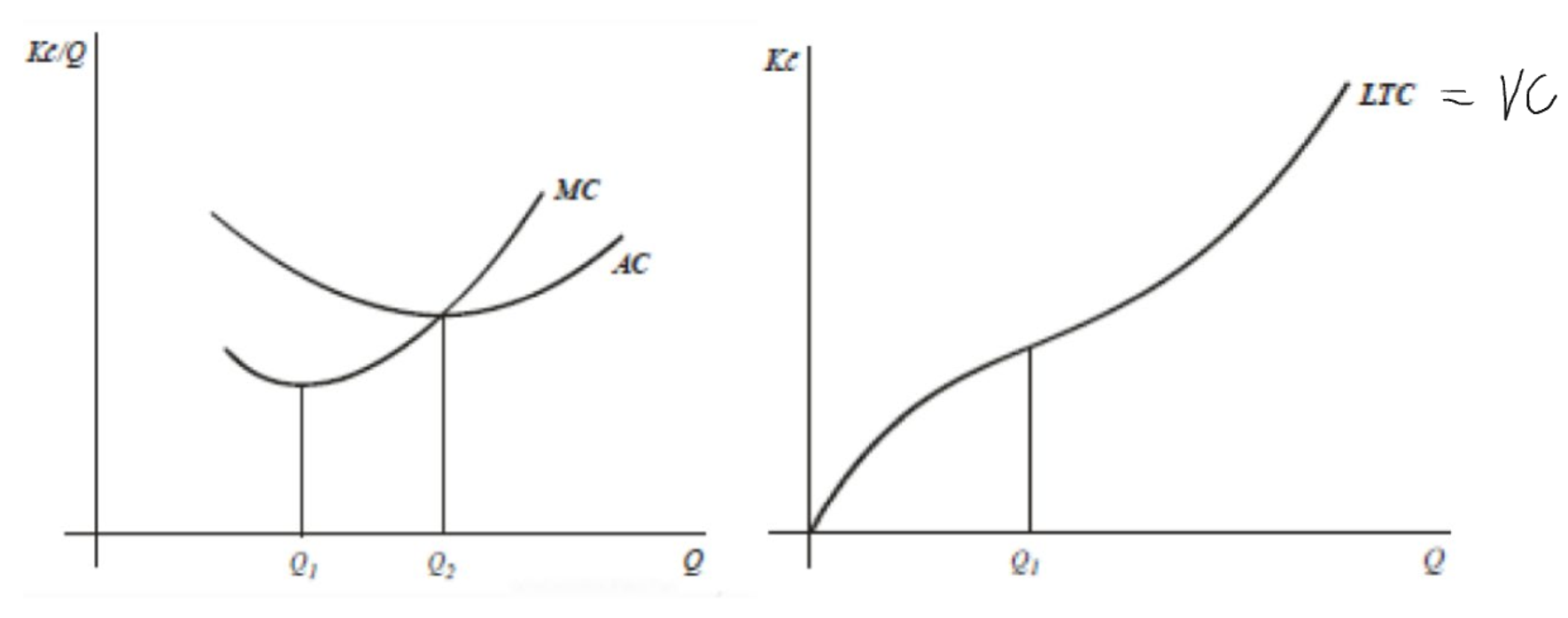
Typy, tvary a vlastnosti nákladů v dlouhém období

Křivky vyjadřující vývoj průměrných a mezních nákladů v DO budou mít stejný tvar jako v krátkém období

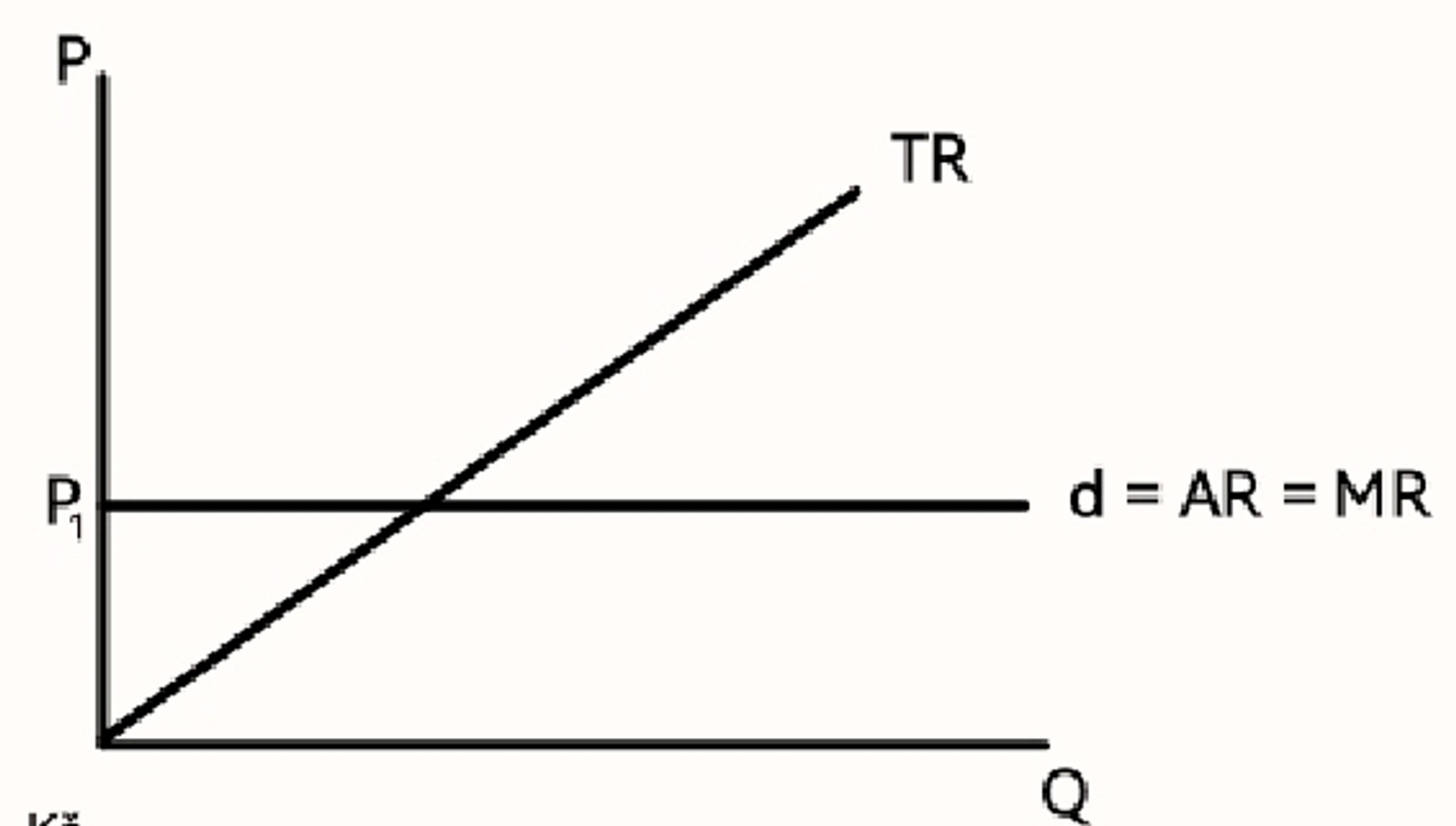
Dokonalá konkurence (definice)

Cena je konstantní → pro všechny firmy stejná → určená poptávkou (dokonale elastická)

Poptávka v dokonalé konkurenci

Dokonale elastická

d=AR=MR=P

Celkové, průměrné a mezní příjmy v podmínkách dokonalé konkurence

• Celkové příjmy TR ⇒ celková částa z prodeje produktů

  • TR = Q \cdot P

• Průměrné příjmy AR ⇒ příjem na jednotku produkce

  • AR = \frac{TR}{Q}=P

• Mezní příjmy MR ⇒ změna celkového příjmu při změně vyrobeného množství

  • MR=\frac{\Delta TR}{\Delta Q}=PB

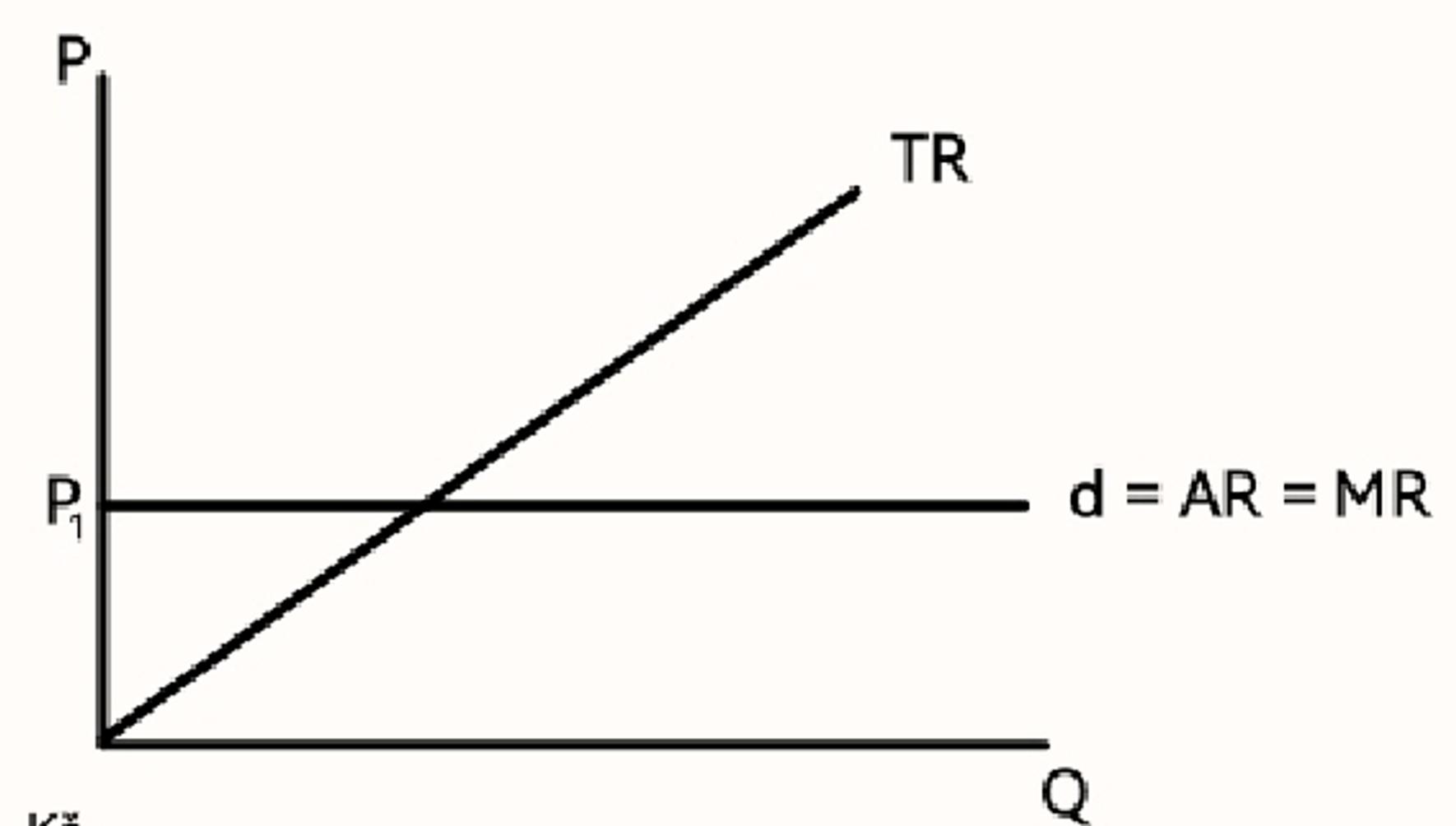
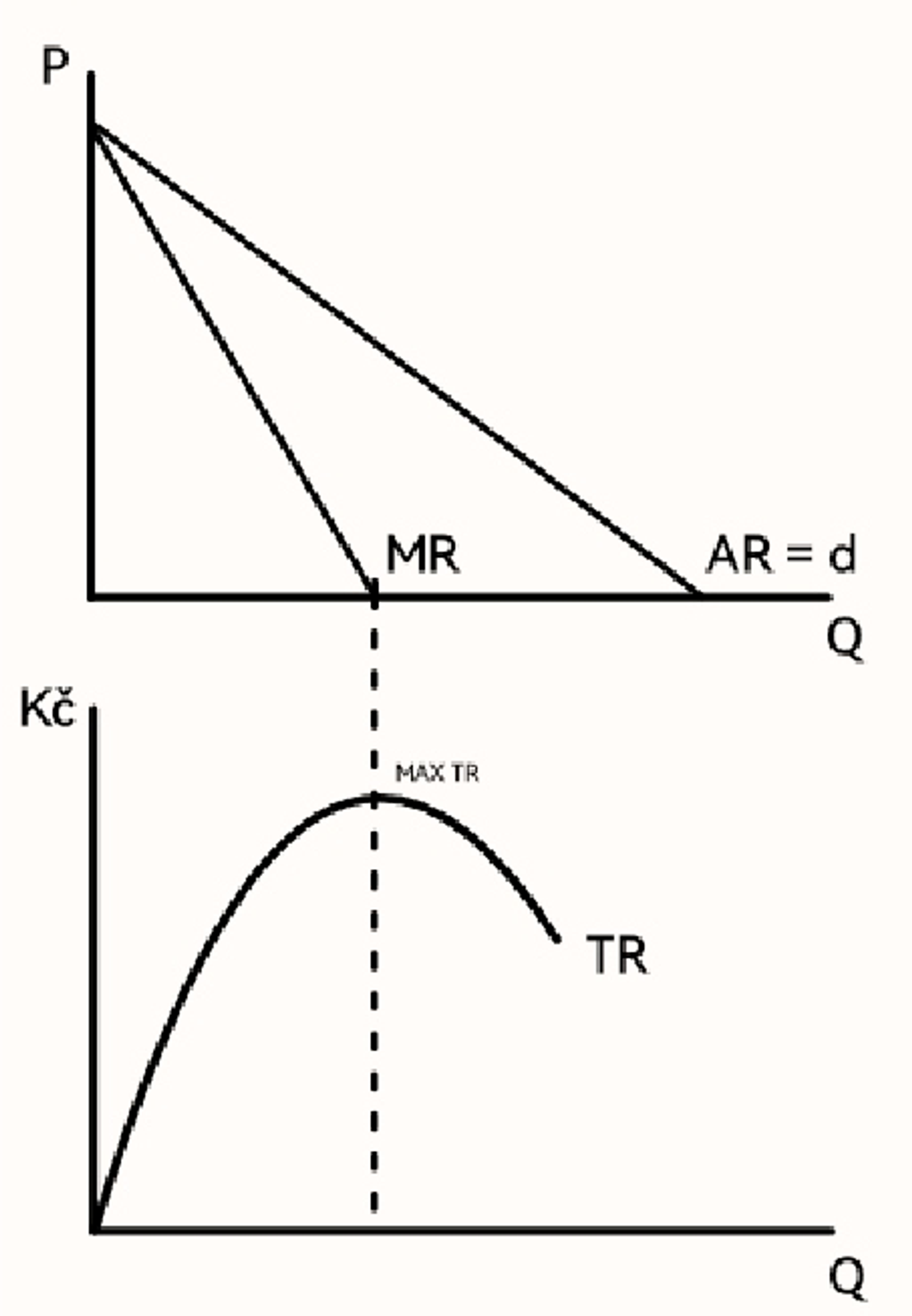
Celkové, průměrné a mezní příjmy v podmínkách nedokonalé konkurence

• Celkové příjmy TR ⇒ celková částa z prodeje produktů

  • TR = Q \cdot P

• Průměrné příjmy AR ⇒ příjem na jednotku produkce

  • AR = d

• Mezní příjmy MR ⇒ změna celkového příjmu při změně vyrobeného množství

  • MR = \frac{\Delta TR}{\Delta Q}

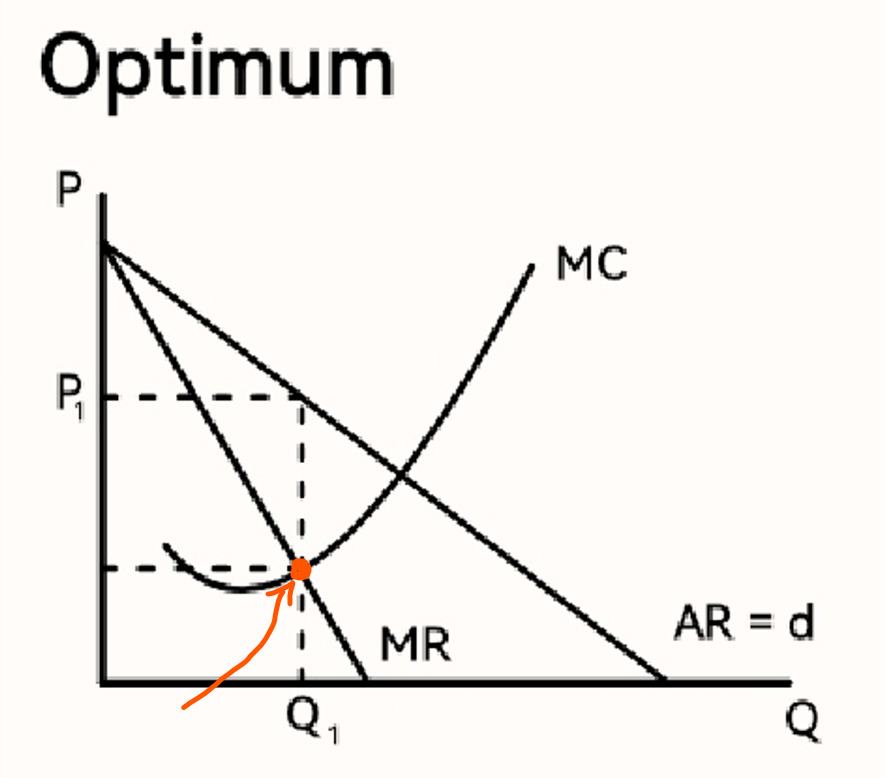
Optimální výše výstupu firmy (zlaté pravidlo maximalizace zisku)

MR=MC

Druhy nákladů

• Explicitní náklady ⇒ Náklady, které musí firma reálně vynaložit v peněžní podobě na nákup výrobních faktorů

• Implicitní náklady ⇒ Ušlý příjem z výrobních faktorů, Náklady obětované příležitosti, Alternativní náklady VF

• Ekonomické náklady ⇒ explicitní + implicitní (= účetní + implicitní)

Zisk firmy (výpočet, druhy)

• Zisk ⇒ příjmy - náklady (= TR - TC)

• Zisk účetní ⇒ příjmy - explicitní náklady

• Zisk ekonomický ⇒ zisk účetní - implicitní náklady

Dokonalá konkurence (charakteristika)

• Cena nezávisí na produkci → určená poptávkou

• Dokonale elastická poptávka

• Dokonalá informovanost kupujících

• Žádné vnější vlivy/bariéry ⇒ všichni mají stejné podmínky

Individuální nabídka firmy v krátkém období, dokonalá konkurence (grarf)

MC = s

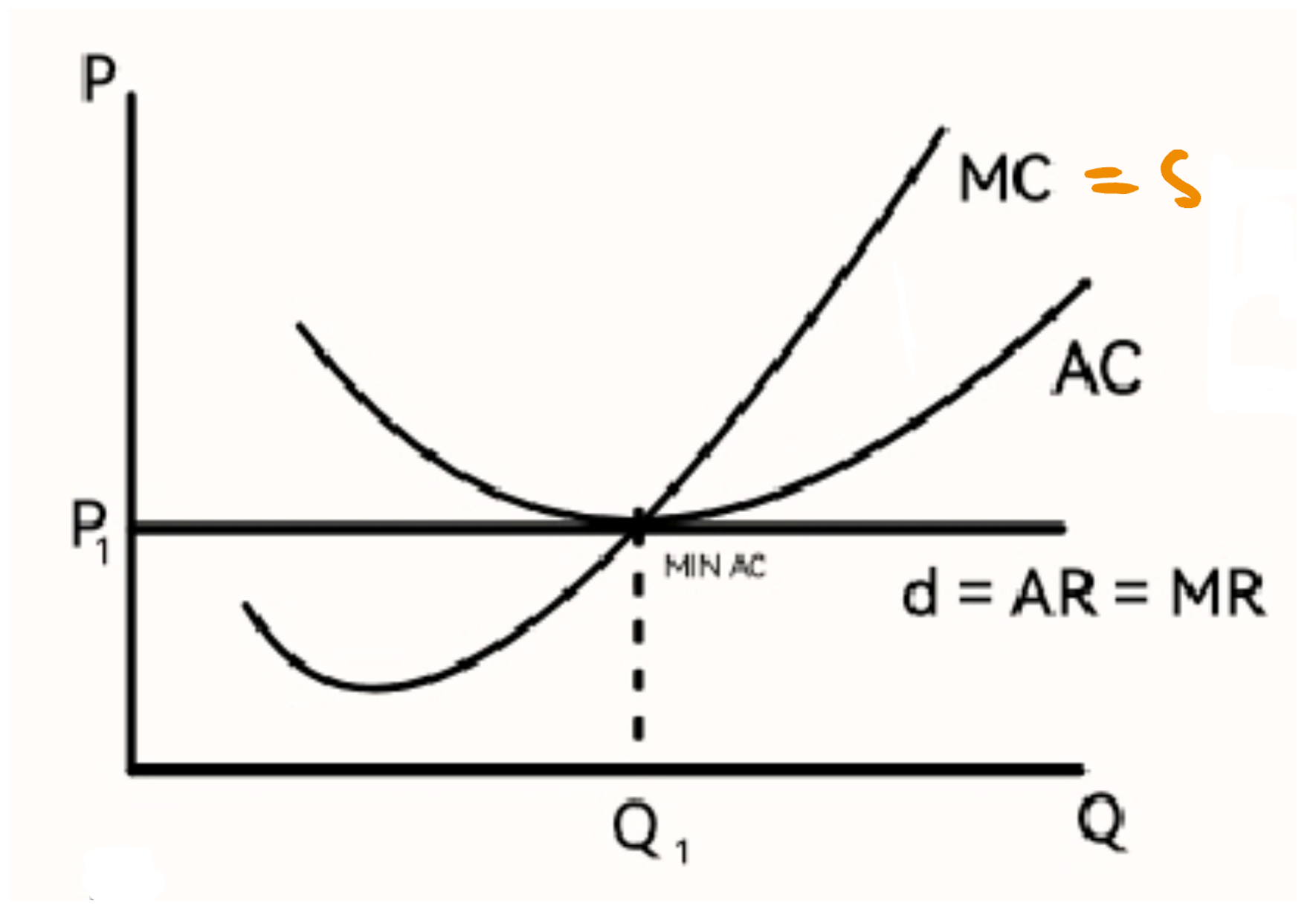
Bod uzavření firmy (definice, graf)

Pokud firma není schopná pokrýt průměrné variabilní náklady AVC, dojde k uzavření firmy.

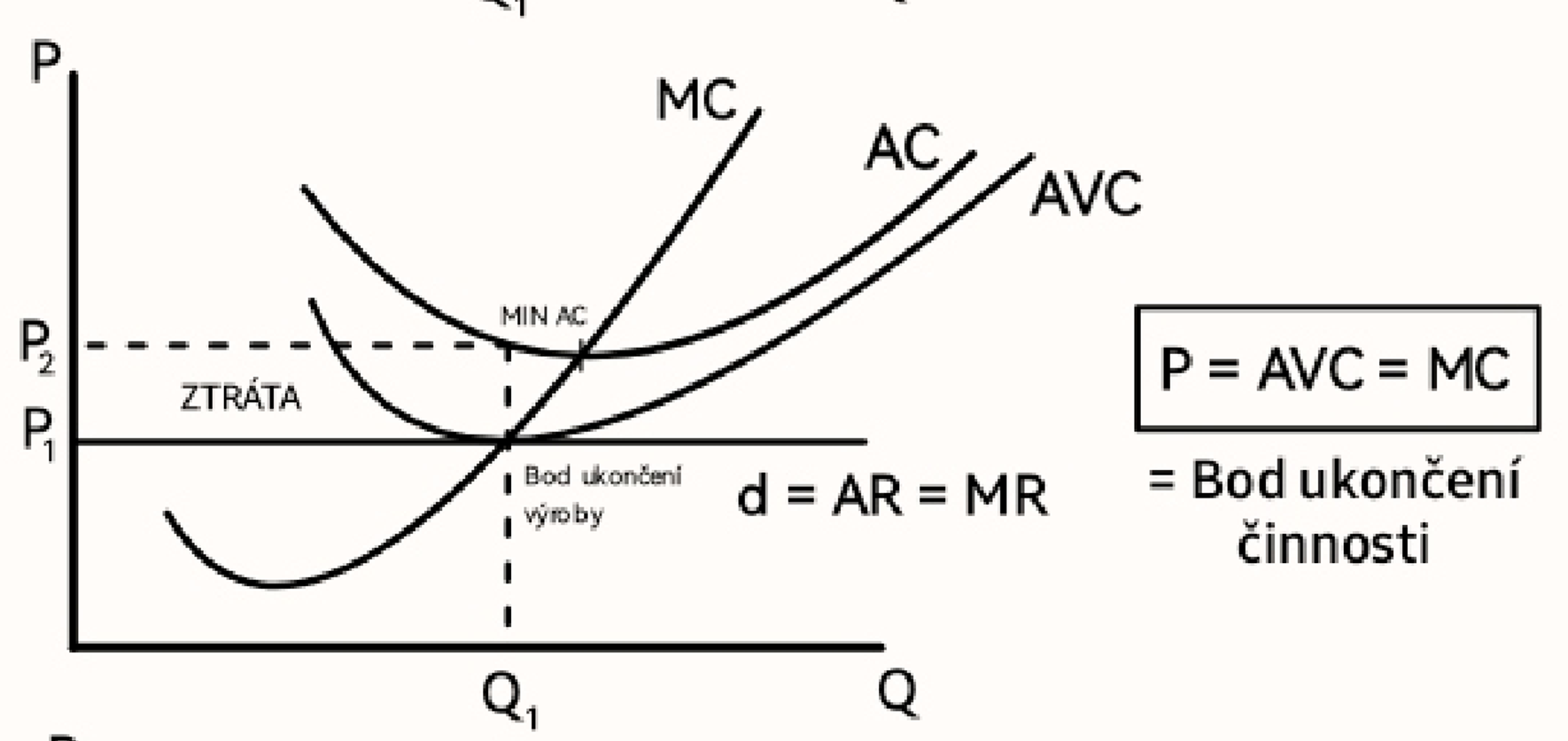
Bod zvratu (definice, graf)

Optimum firmy v dlouhém období

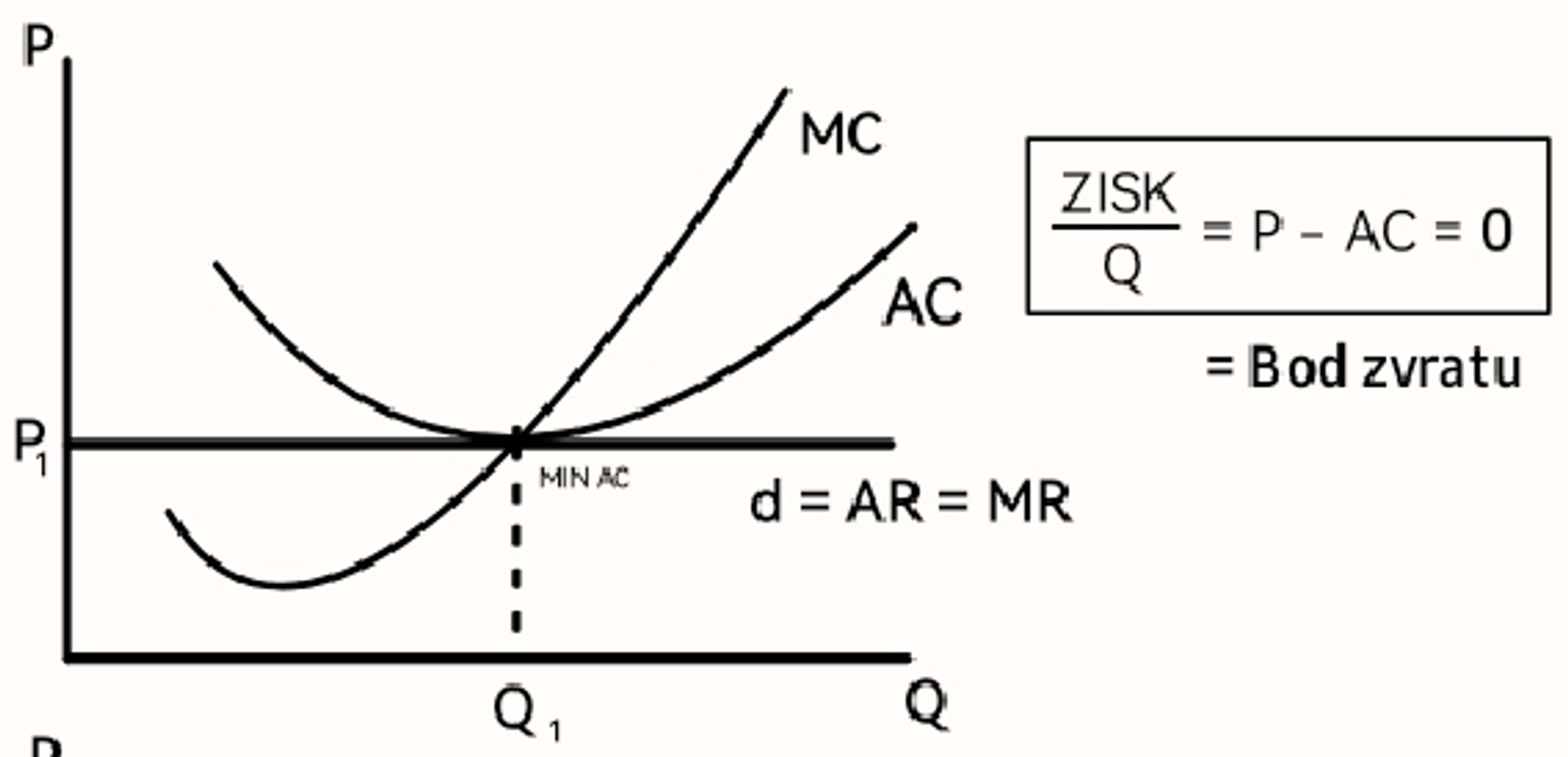
Cenová elasticita nabídky (definice)

Citlivost změny nabízeného množství na změnu ceny

Elasticita nabídky z hlediska časového období

Ve velmi krátkém období je nabídka zcela neelastická, s prodlužováním časového horizontu se elasticita nabídky zvyšuje

Cenová elasticita poptávky (definice, vzorec)

Citlivost poptávky na změnu ceny

\text{cenová elasticita poptávky} = \frac{\% \Delta \ \text{poptávaného množství (Q)}}{\% \Delta \ \text{ceny (P)}}

Druhy elasticity

• Elastická: E>1

  • Vyplatí se snížit cenu (TR klesá)

• Jednotková: E=1

  • Ideální stav

• Neelastická: E<1

  • Vyplatí se zdražit (TR roste)

• Dokonale elastická: E=∞

  • I nepatrná změna ceny má nekonečný vliv na odezvu poptávky.

• Dokonale neelastická: E=0

  • Nabídka nebo poptávka po daném zboží je zcela nezávislá na její ceně.

Elasticita poptávky E>1, firma by měla…

Snížit cenu

Elasticita poptávky E<1, firma by měla…

Zvýšit cenu

Tržní nabídka

Součet objemu výroby určitého zboží, které jsou ochotni při různých úrovních ceny nabízet všichni výrobci tohoto zboží.

Součet všech individuálních nabídkových křivek

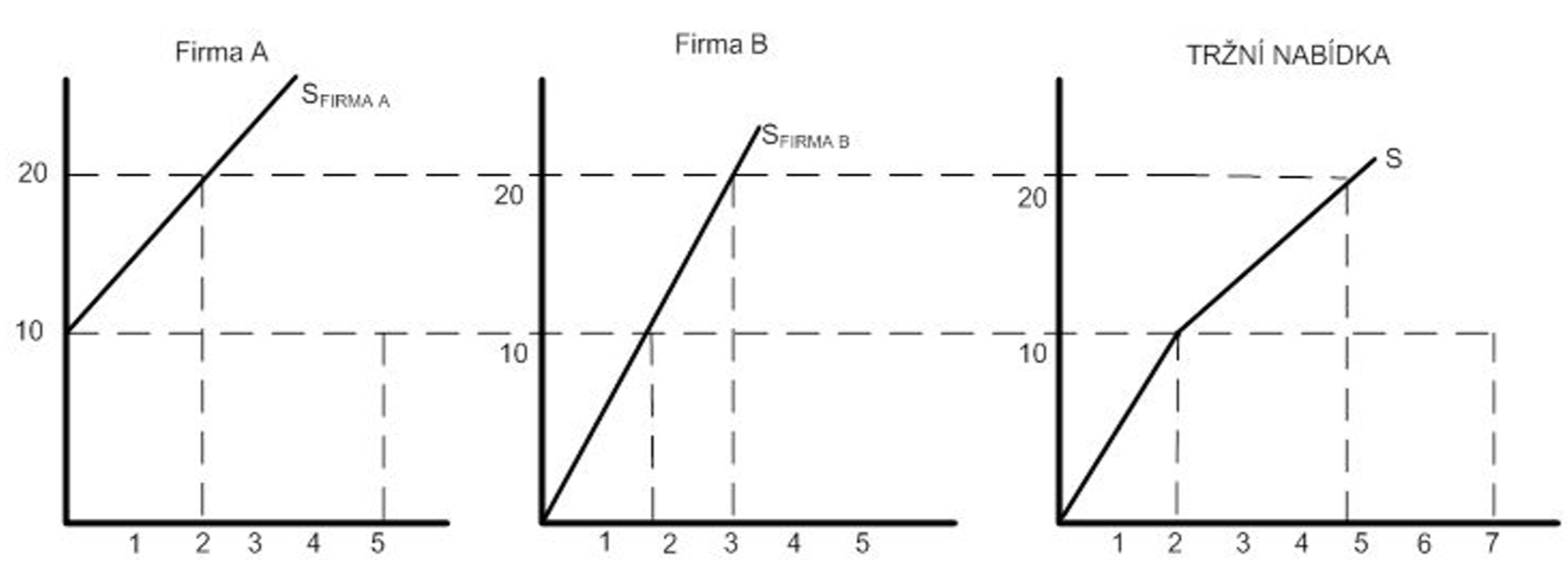
Tržní rovnováha (definice, graf)

Nastává v optimu spotřebitele a výrobce

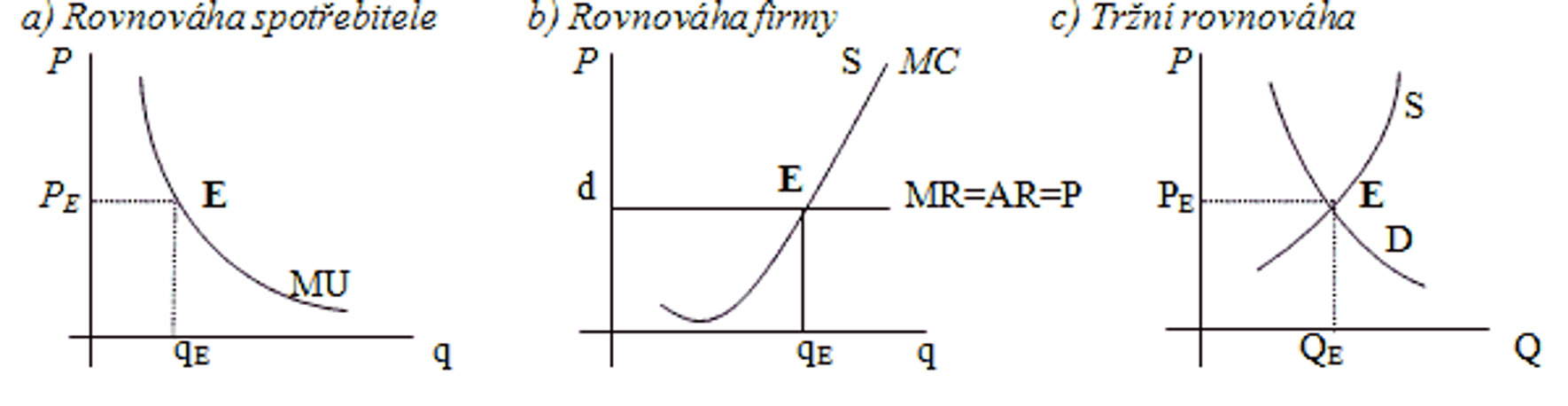
Výhody ze směny (typy, graf)

• Přebytek spotřebitele: rozdíl mezi celkovým užitkem a objemem výdajů na nákup

• Přebytek výrobce: rozdíl mezi cenou a mezními náklady

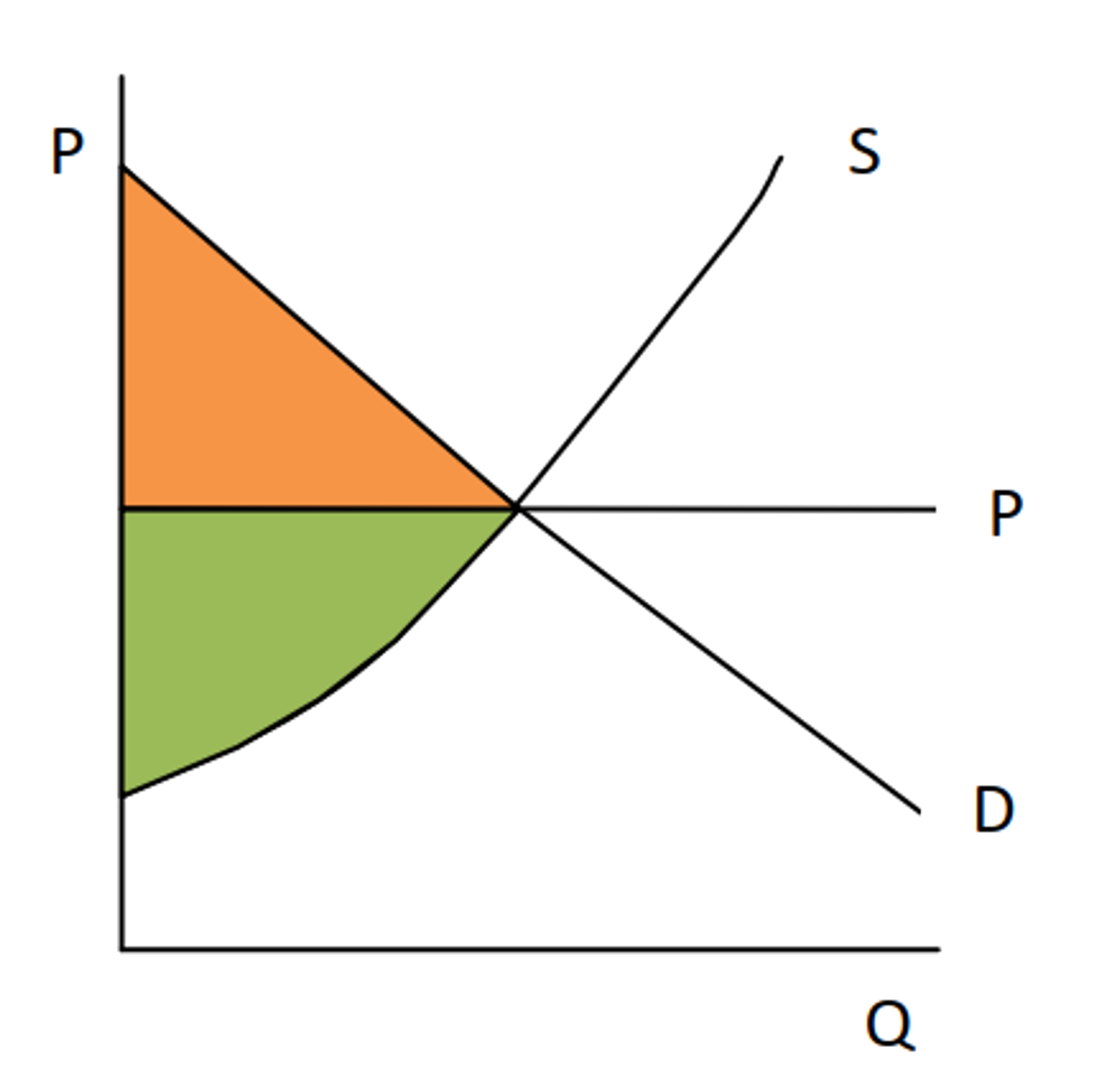
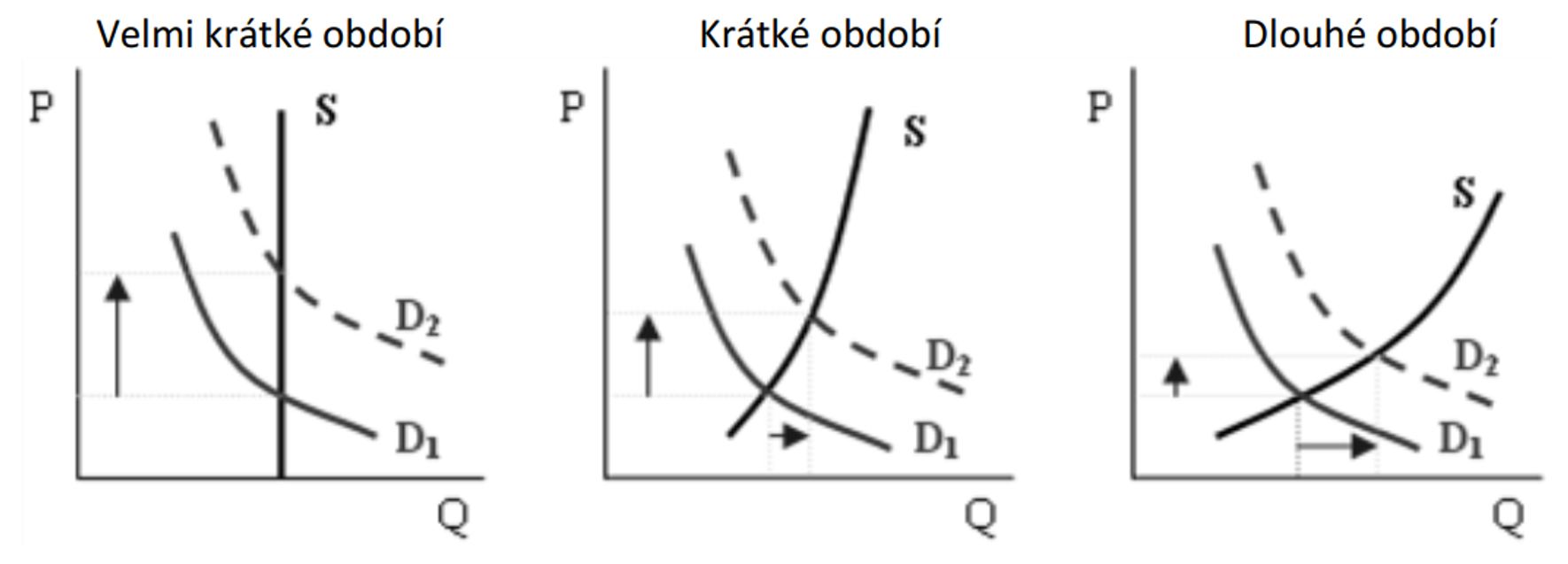
Rovnováha z hlediska délky období

• Velmi krátké období: nabídka je zcela neelastická; růst poptávky vyvolá pouze růst ceny

• Krátké období: elasticita je vyšší; růst ceny je nižší

• Dlouhé období: elasticita je ještě vyšší; pohyb ceny je ještě nižší

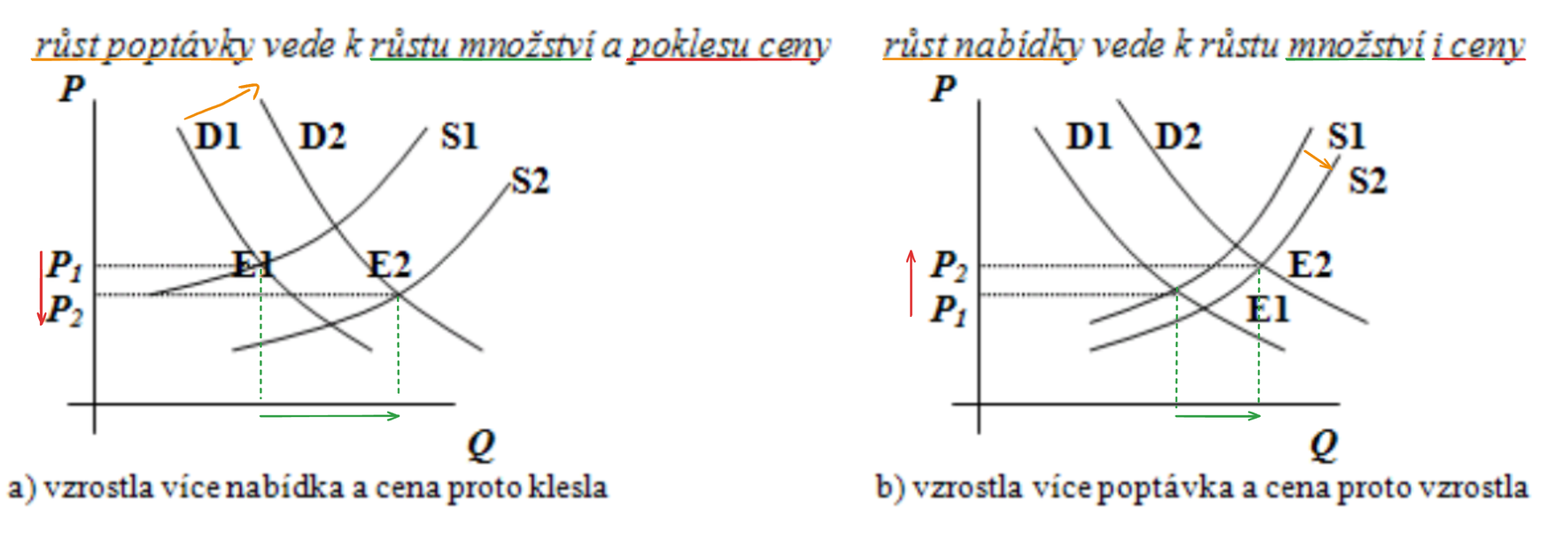
Rovnováha a současná změna nabídky a poptávky

Teorém pavučin (definice, typy)

Lidé, ale i výrobci, potřebují určitý čas, než přizpůsobí objem svých nákupu či výroby

1. Konvergující pavučina

2. Divergující pavučina

3. Stabilní pavučina

4. Oscilující pavučina

Konvergující pavučina (definice, graf)

křivka poptávky má větší sklon než křivka nabídky (obnovuje rovnováhu)

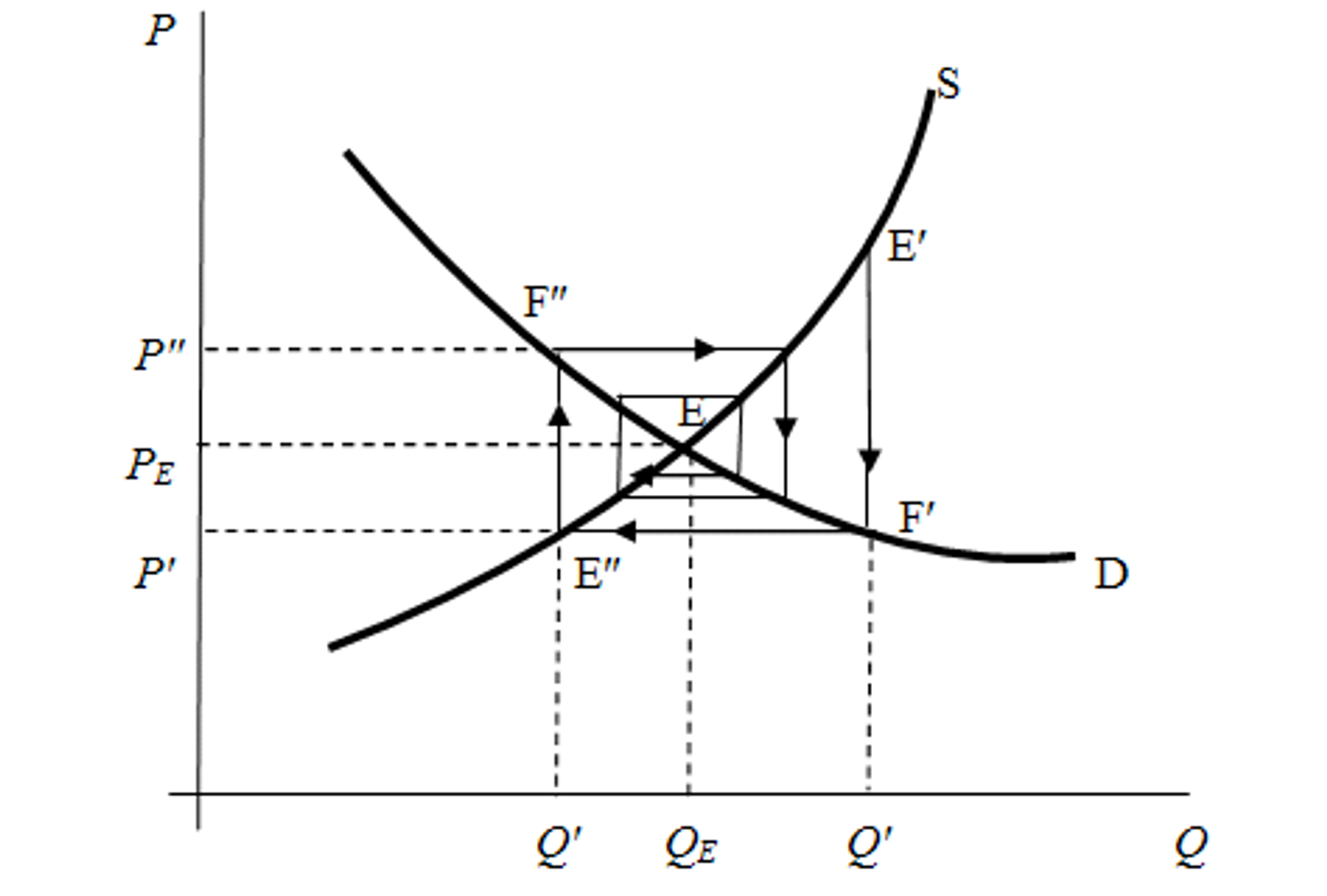
Divergující pavučina (definice, graf)

křivka poptávky má větší sklon než křivka nabídky (prohlubuje nerovnováhu)

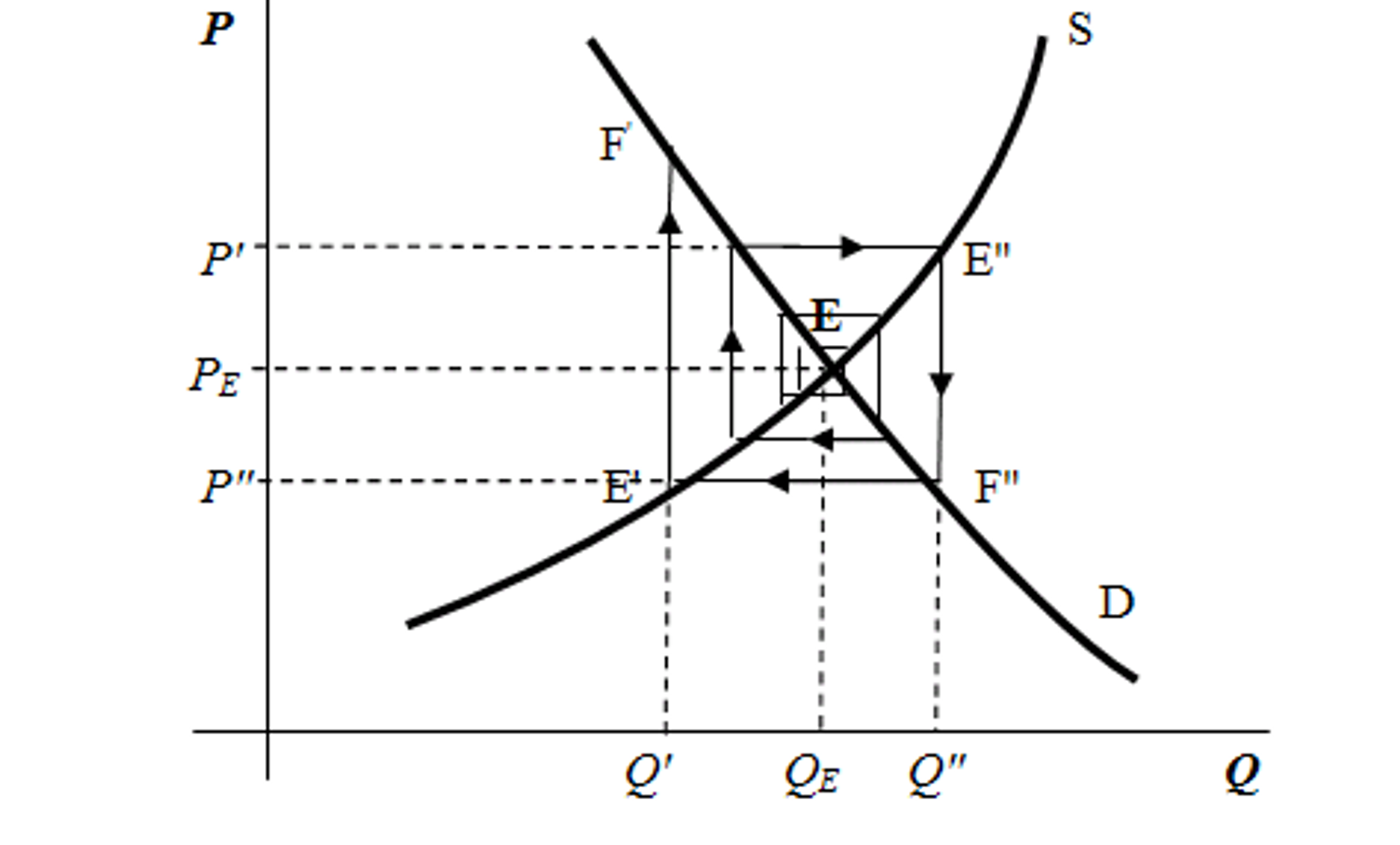
Stabilní pavučina (definice, graf)

sklon nabídky i poptávky se rovná (rovnováha je furt stejná)

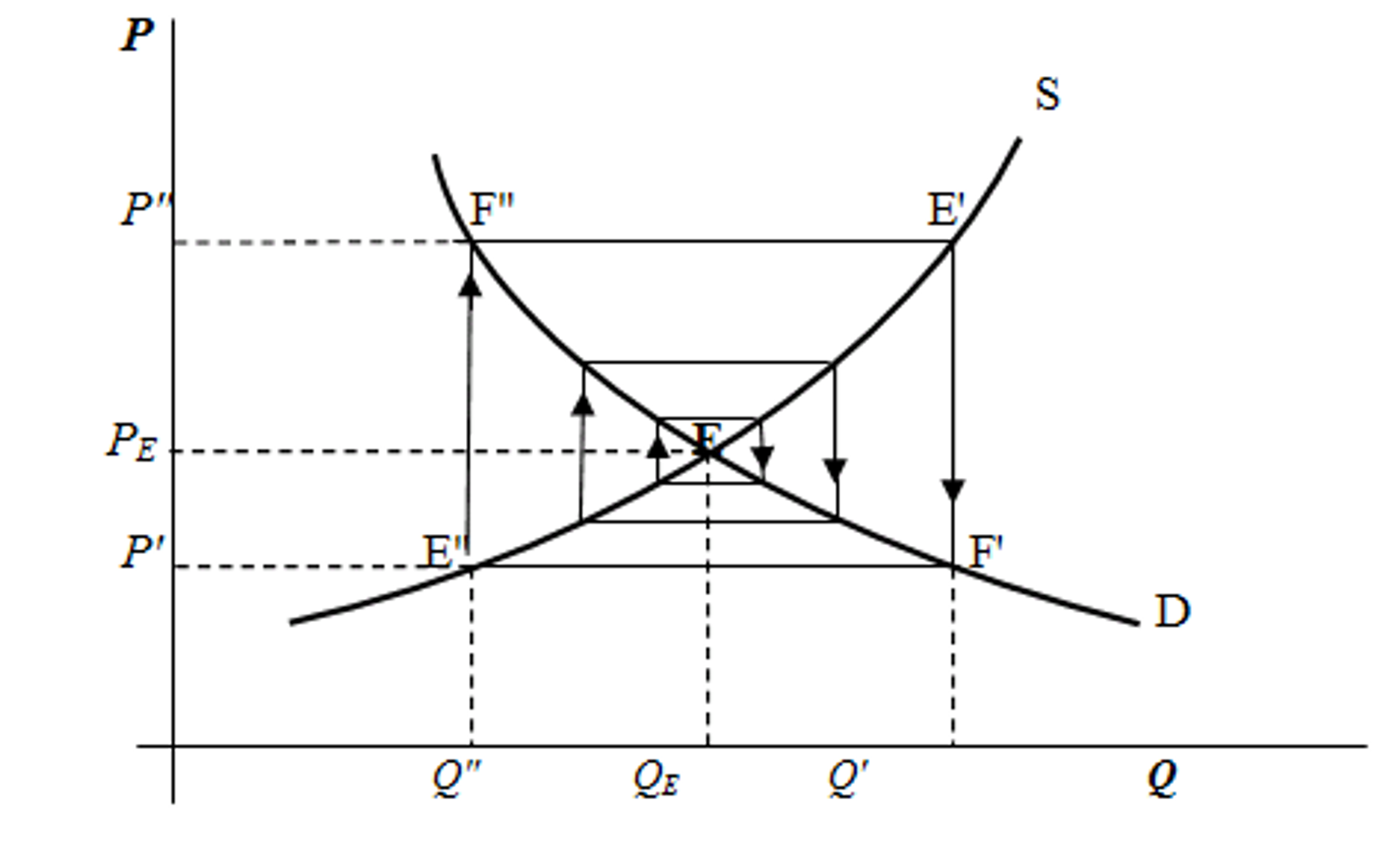
Oscilující pavučina (definice, graf)

sklon nabídky i poptávky se rovná (prohlubování nerovnováhy, ale je zastavení)

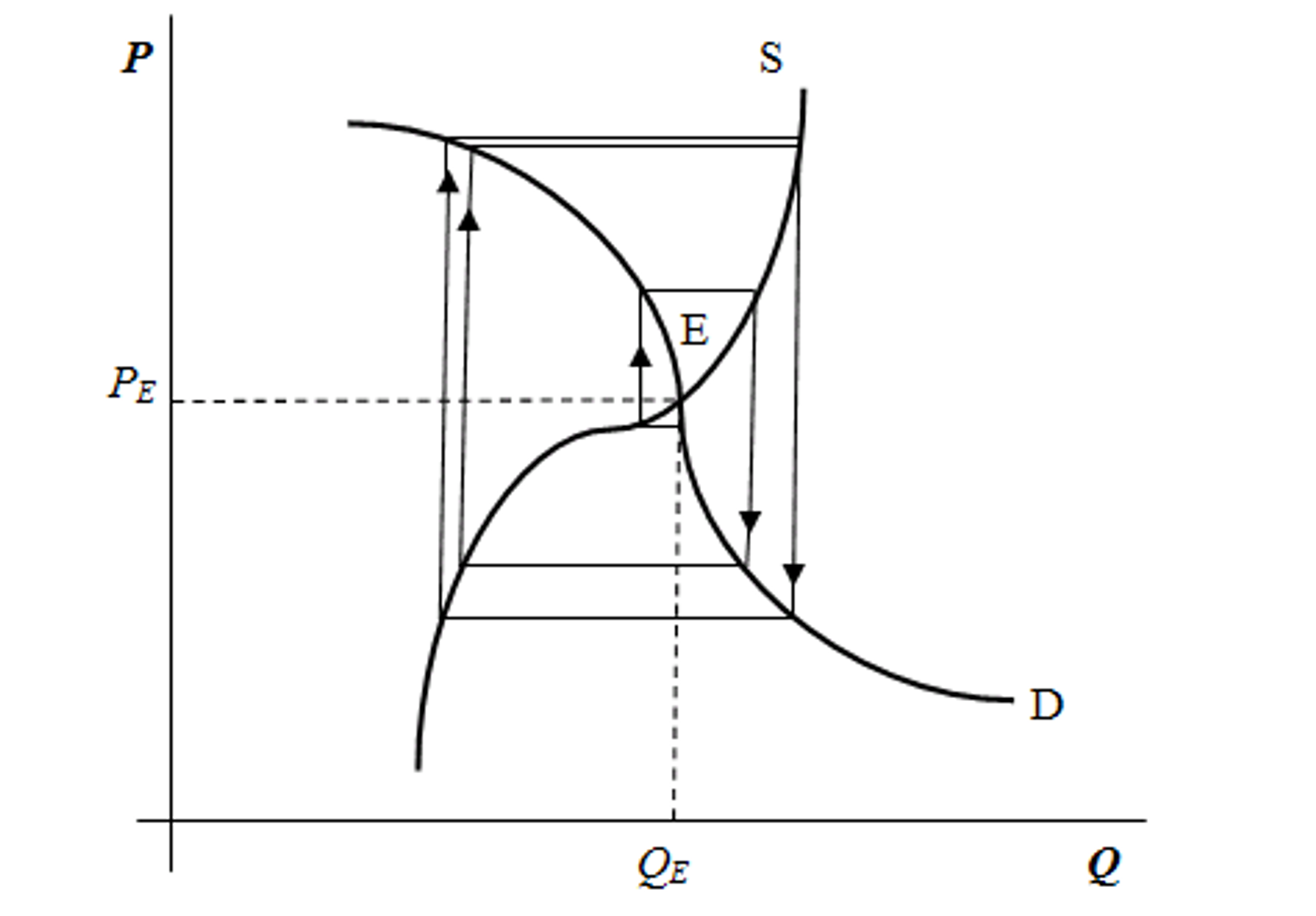
Příčiny existence nedokonalé konkurence

• Nákladové podmínky: velké firmy vyrábějí levněji → vytlačení slabší konkurence

• Bariery konkurence:

  • Právní restrikce: ochranné známky, patenty, copyright

  • Diferenciace produktu: produkty se nějak liší od jeho konkurece

• Další:

  • Nedostatečné informace tržních subjektů

  • Vlastnictví důležitého výrobního faktoru

  • Zásahy státu do tržního mechanismu (regulace cen)

  • Politické okolnosti (OPEC)

Společné rysy dokonalé a nedokonalé konkurence

• MC = MR ⇒ maximalizace zisku (zlaté pravidlo)

• \pi=TR-TC ⇒ zisk = celkové příjmy - celkové náklady

• Nákladové křivky jsou shodné ⇒ determinované produkční funkcí

  • Krátké období: TC=FC+VC

  • Dlouhé období: TC = VC

• AR=P=d ⇒ průměrné příjmy = cena = individuální poptávka

Rozdílné rysy dokonalé a nedokonalé konkurence

• Určování ceny

• Vnější vlivy na firmu

• Křivka poptávky a příjmů

• Elasticita poptávky

• Monopolní síla

• Vztah mezi cenou a prodaným množstvím

• Bod, kdy firma dosahuje normálního zisku

Typy firem v tržní ekonomice

1. Státní a municipální firmy

   • vlastníkem firmy je stát nebo obec

2. Firmy v individuálním vlastnictví

   • podnikatel hospodaří sám na vlastní účet

3. Obchodní společnosti ****(partnerství)

   • jde o sdružení kapitálu dvou i více osob

4. Akciová společnost

   • větší možnosti získání kapitálu vydáním akcií

Alternativní cíle firmy

Není-li možná maximalizace zisku, protože firma nemá dostatek informací:

1. dosažení uspokojivé výše zisku

2. dosažení určitého podílu na trh

3. snaha dlouhodobě přežít

4. růst a expanze firmy

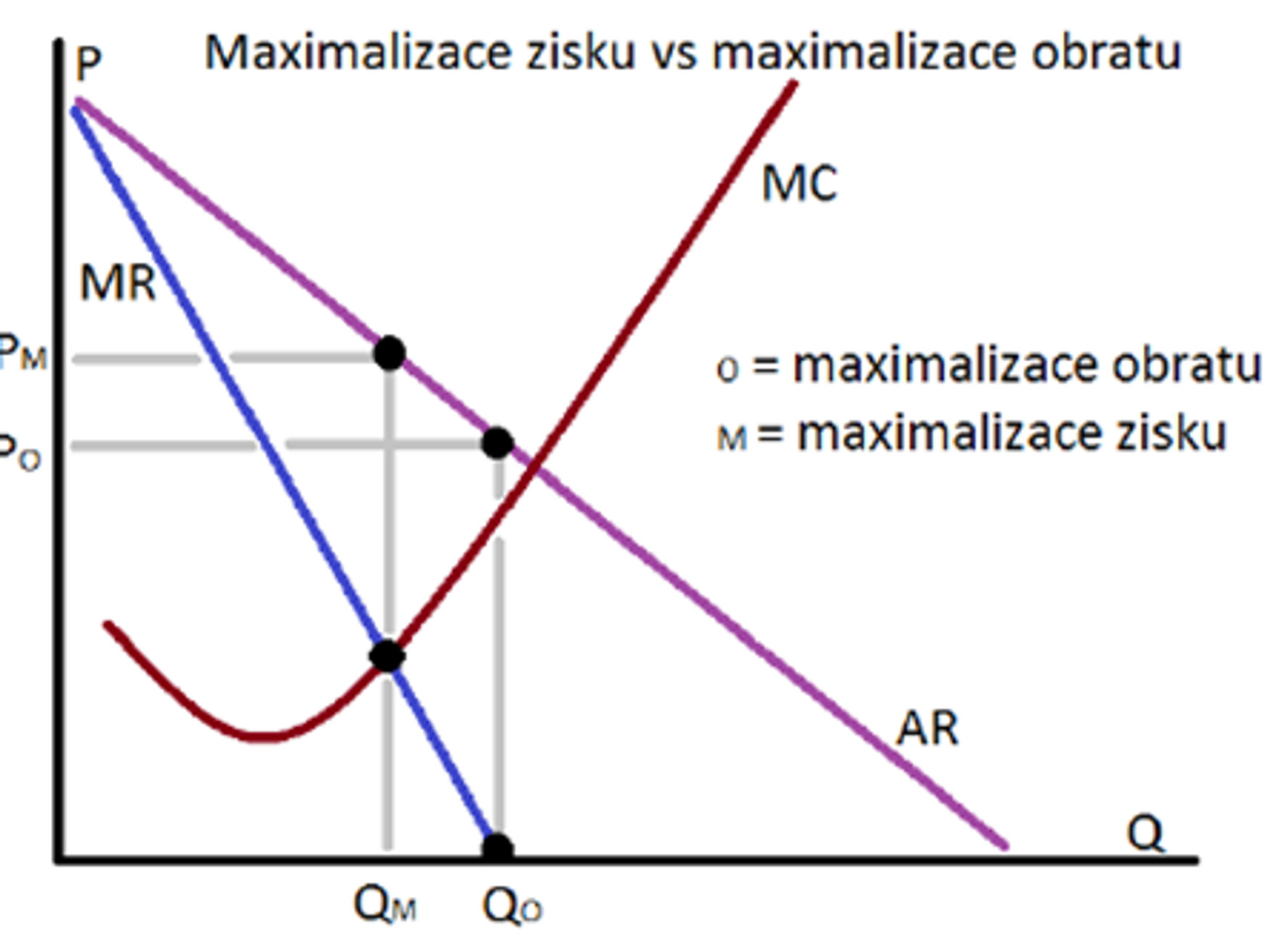
Firma maximalizující obrat VS. maximalizující zisk (definice, znázornění na grafu)

• Obrat:

  • Vyrábí větší objem za nižší cenu

  • 𝑀𝑅 < 𝑀𝐶

• Zisk:

  • MR = MC

Formy nedokonalé konkurence

• Monopol

• Oligopol

• Monopolistická konkurence

Monopol (definice, graf)

• Pouze jeden výrobce na trhu ⇒ nemá konkurenci

• Má veškerou produkci daného odvětví

• P > MC ⇒ firma si může určit téměř libovolně vysokou cenu

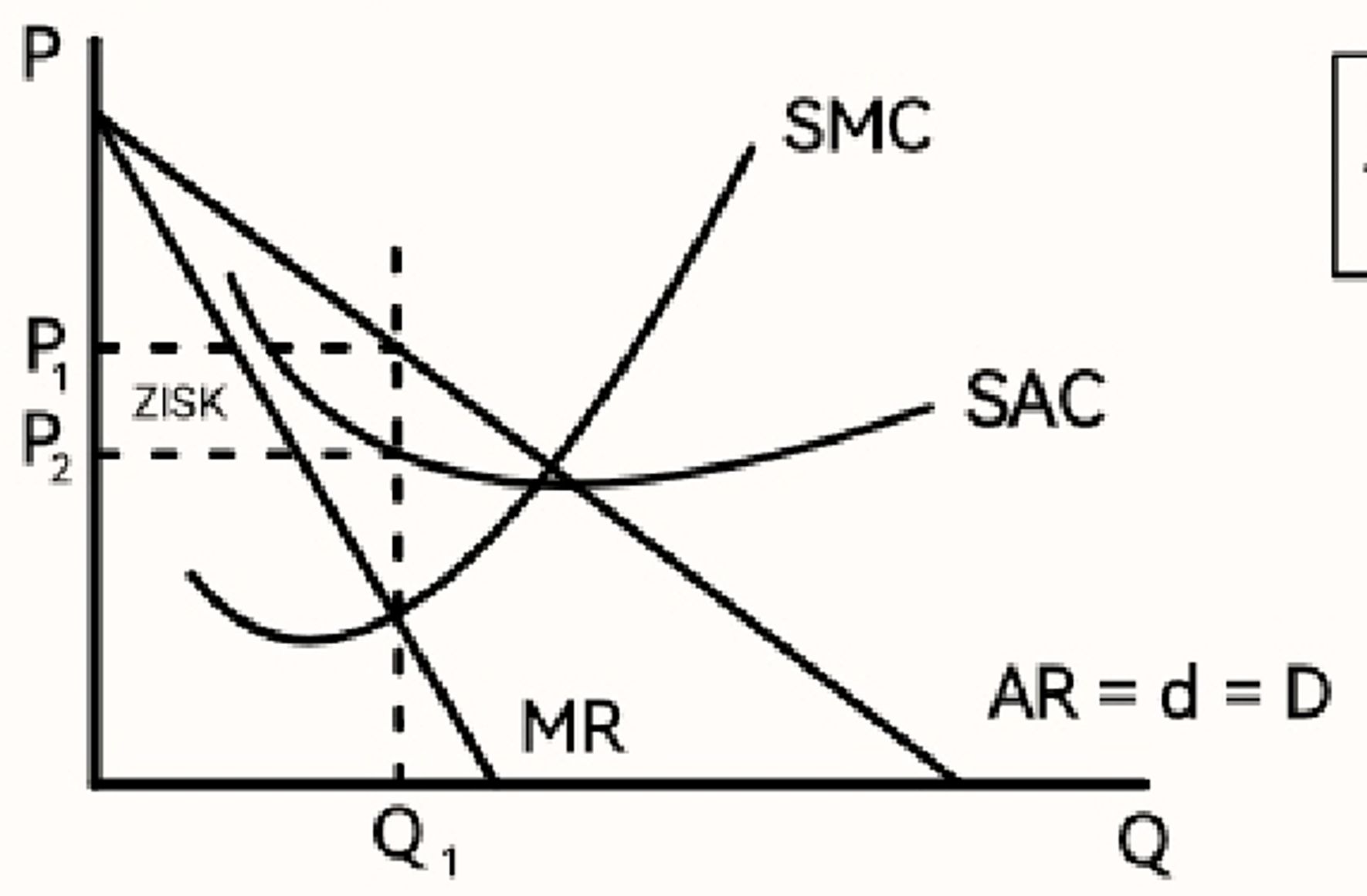
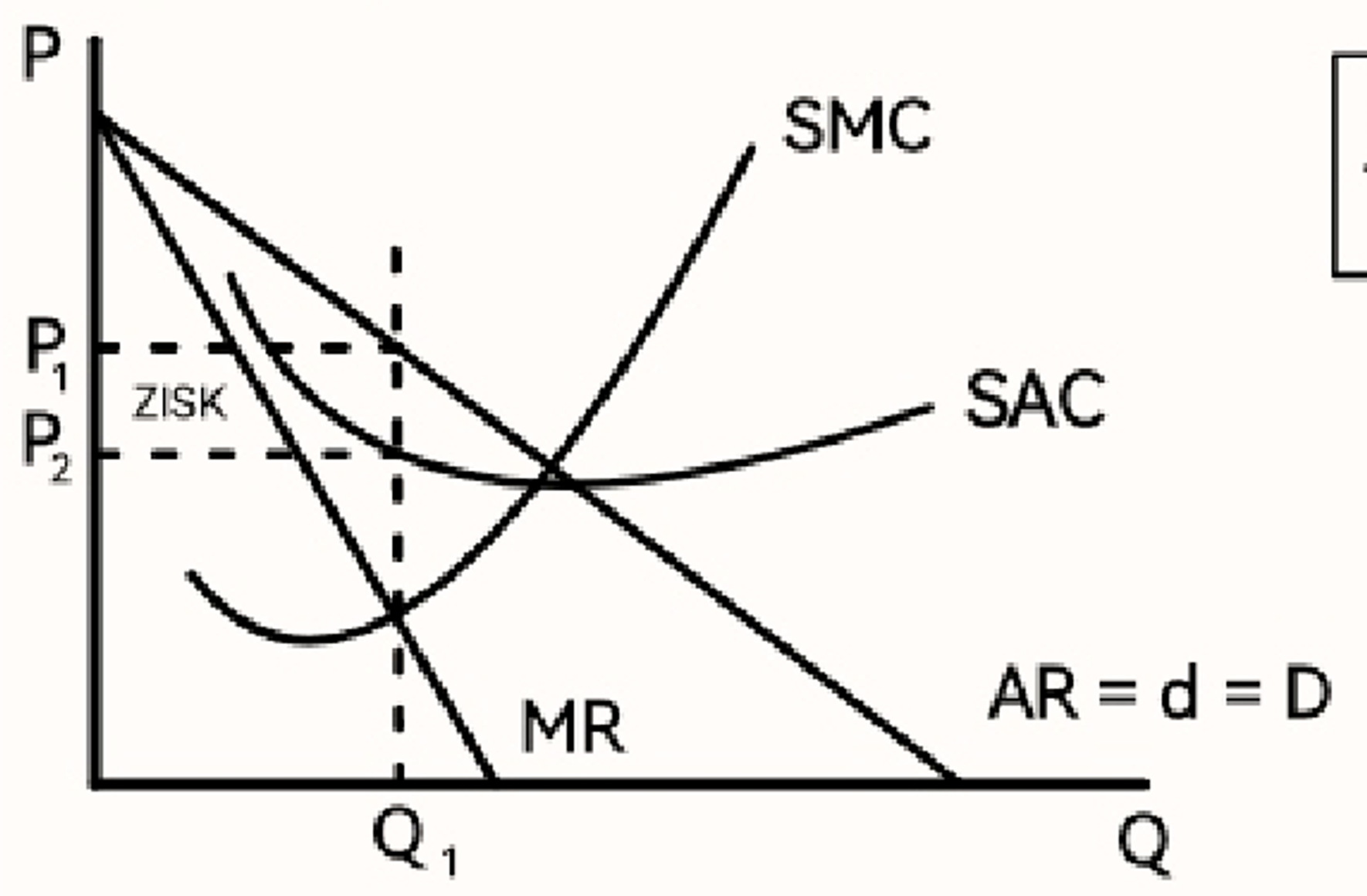
Monopol (graf)

Lernerův index (definice, vzorec)

stupeň tržní (monopolní) síly

L=\frac{(P-MC)}{P}

Nabývá hodnotu mezi 0 (dok. konkurence) a 1 (mopol)

Neefektivnost monopolu (graf)

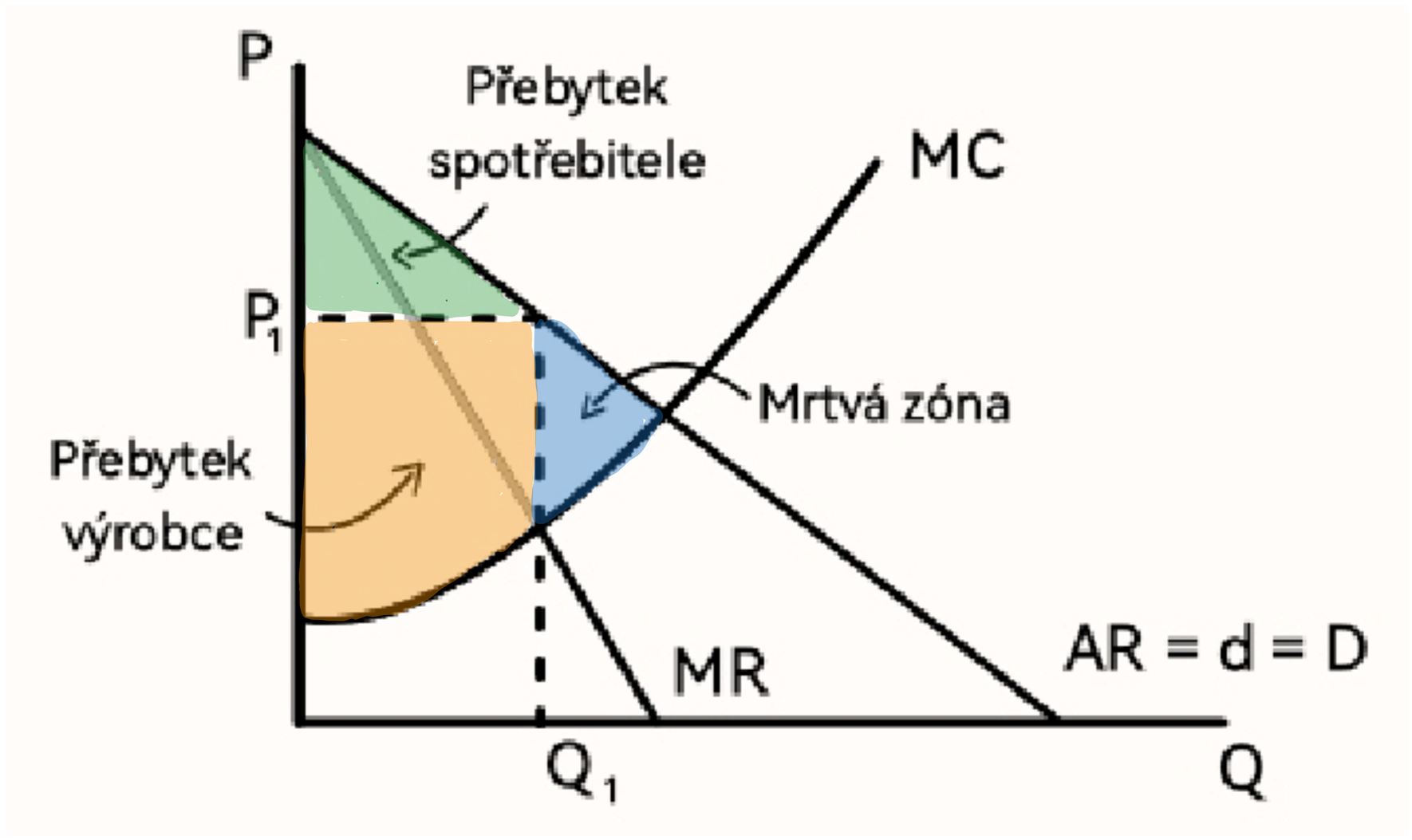
Regulace monopolu

• V ČR Úřad pro ochranu hospodářské soutěže

• Antitrustové zákony

  • Zakazují určité chování firem (dohody o cenách, spojování)

• Ekonomická regulace

  • Regulace cen zákony → aby pokryly jen průměrné náklady

Monopson

Na trhu jen jeden kupující ⇒ může ovlivňovat cenu

Oligopol

• Malá skupina firem v odvětví

• Velké bariéry ve vstupu do odvětí

Smluvní oligopol (definice, graf)

• Kartel → nelegální

• Oligopolní firmy se navzájem domluví na ceně

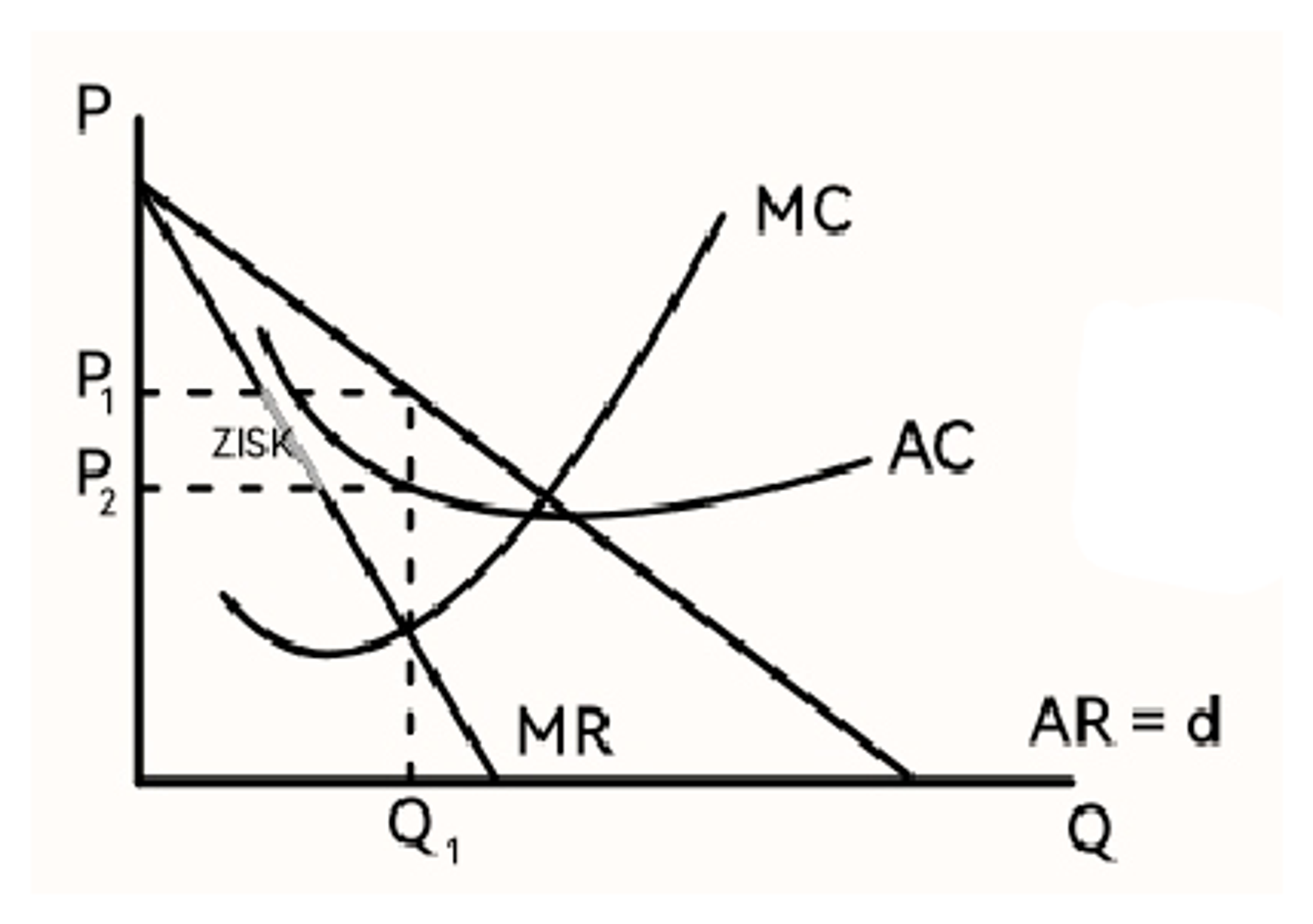
Oligopol s dominantní firmou (definice, graf)

• Jedna silná firma, skoro jako monopol

• Další menší firmy (konkurenční lem)

Monopolistická konkurence (definice)

• Normální trh

• Hodně firem prodává podobné výrobky

• Snadný vstup a výstup do odvětví

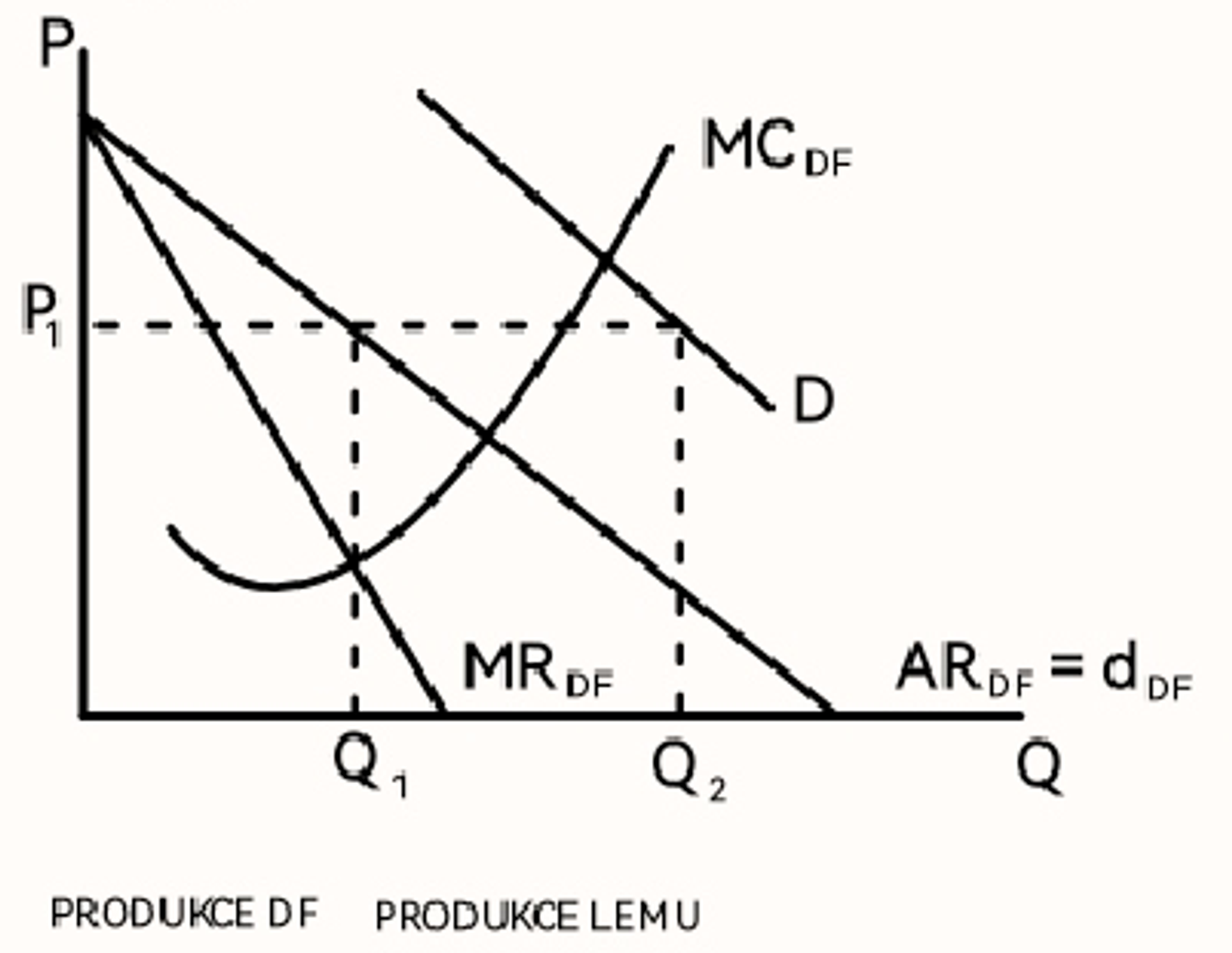
Monopolistická konkurence v krátkém období (graf)

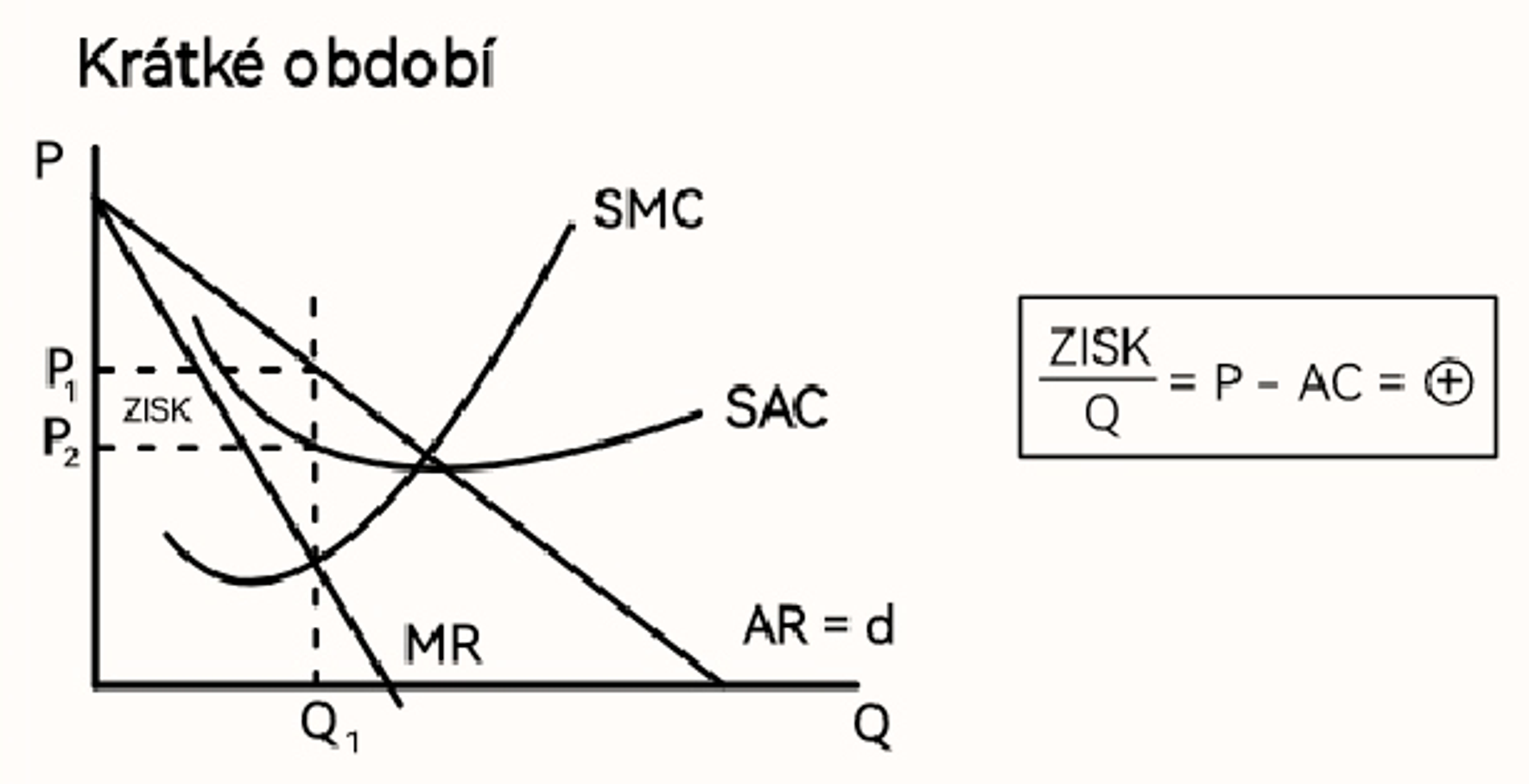
Firma v monopolistické konkurenci a krátkém období mající záporný zisk

• vyrábí dál, cíl ztrátu minimalizovat, očekávání změny na trhu → AC > AR ; AVC < AR

• až do bodu uzavření firmy → TR = VC ; Ztráta = FC

Firma tedy musí pokrýt alespoň své fixní náklady

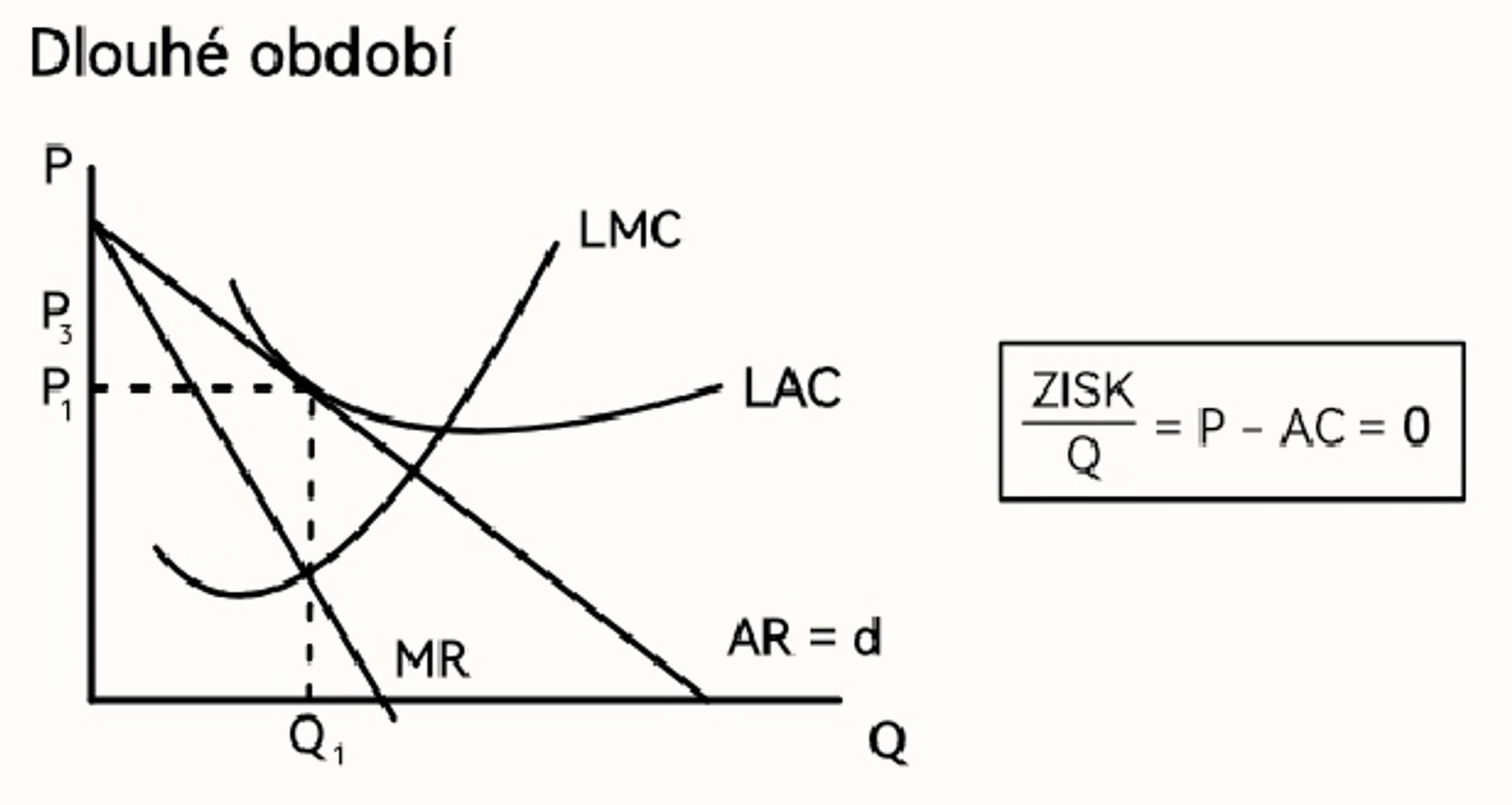
Dlouhé období v monopolistické konkurenci (definice, graf firmy)

• Možnost přechodu mezi odvětvími

• Ztrátové odvětví nemůže dlouhodobě existovat = krach firmy

• Ziskové odvětví, dobře se vydělává, přichází noví podnikatelé a zakládají nové firmy

• Vzrůst počtu výrobců → pokles poptávky, nová cena = nulový zisk

Podstata a specifika trhů výrobních faktorů

Firmy poptávají, domácnosti nabízejí

Transferový výdělek

Minimální výdělek, za který jsem ochotný pracovat na dané pozici

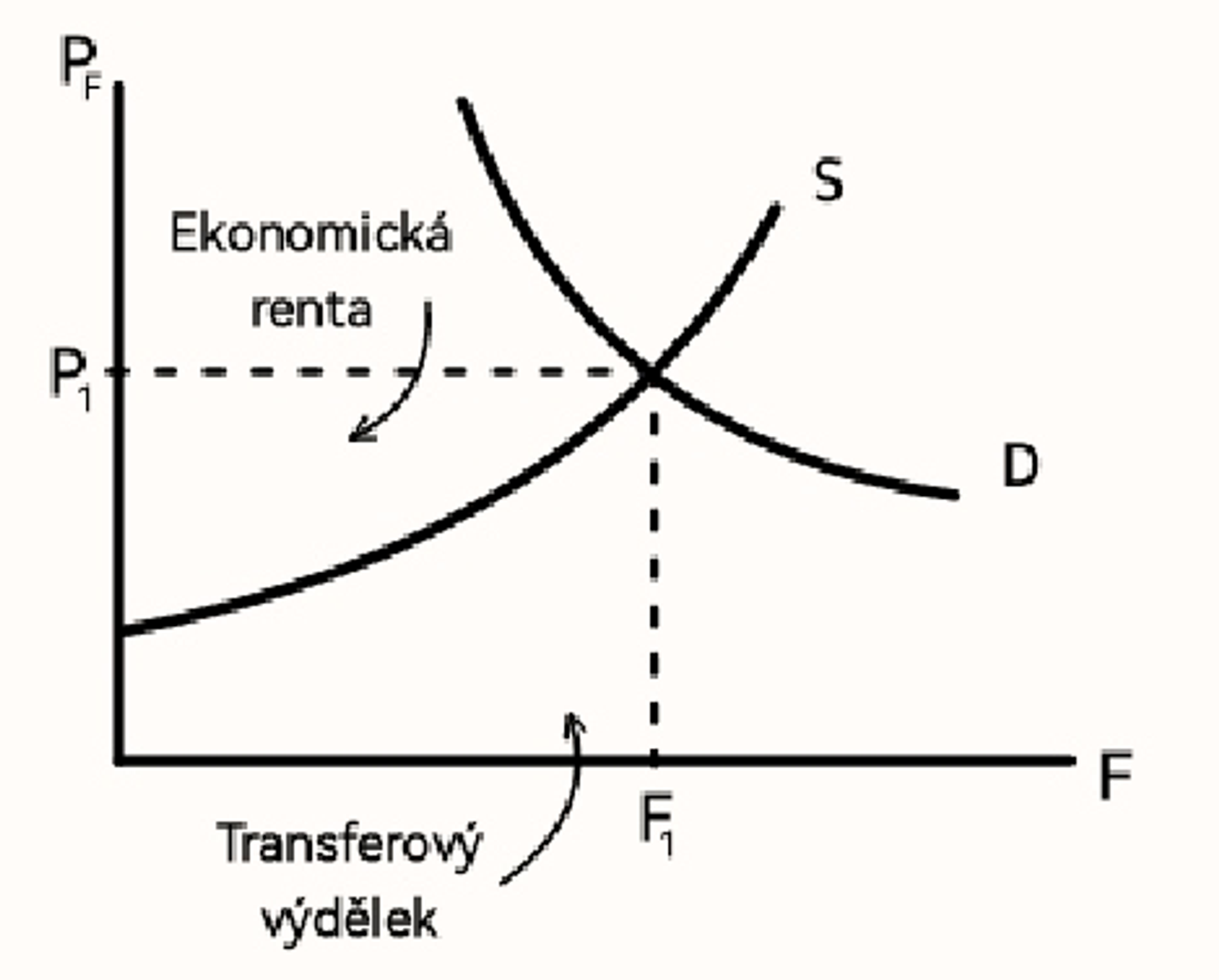
Ekonomická renta

To co mám navíc oproti mému transferovému výdělku

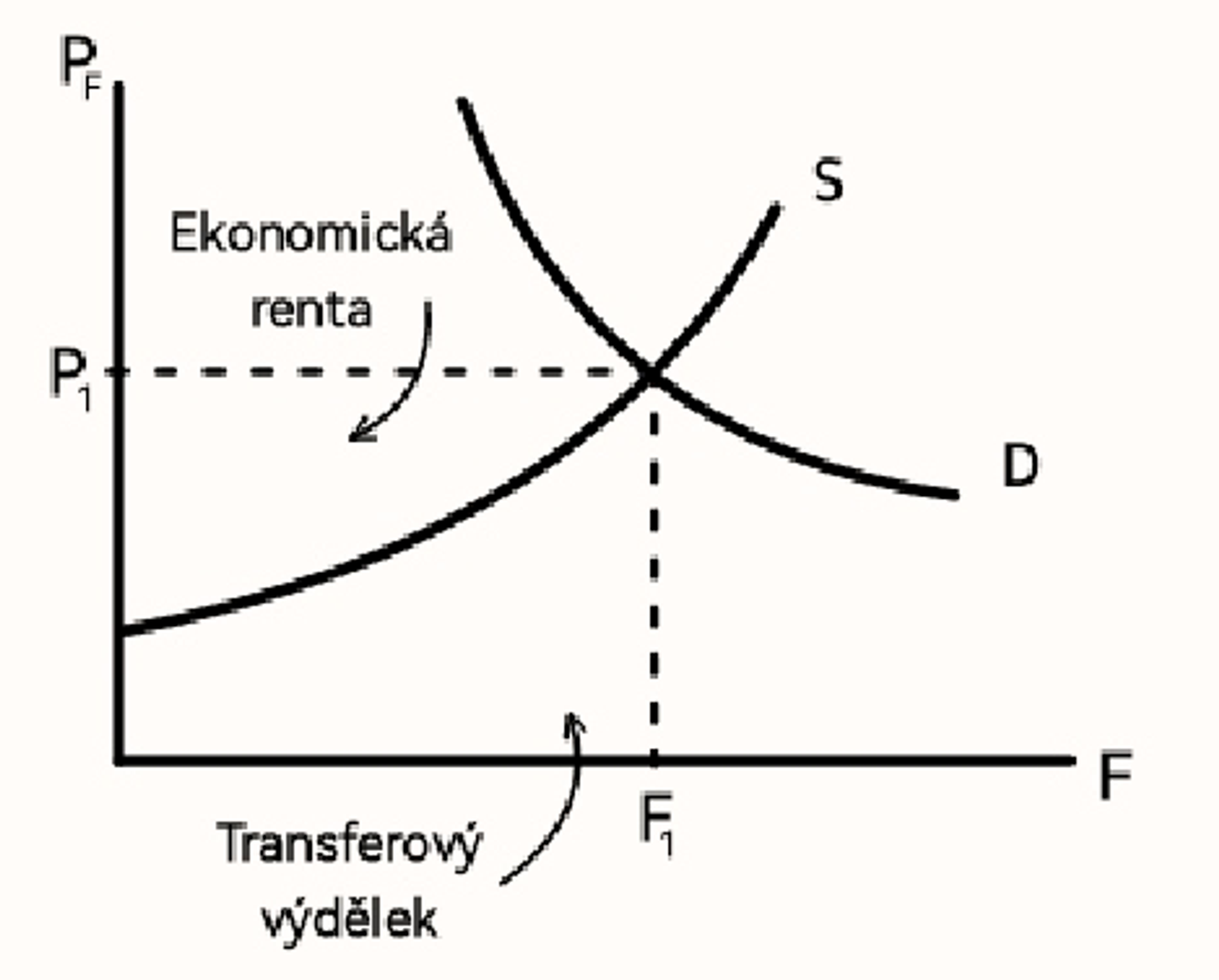
Transferový výdělek a Ekonomická renta z hlediska elasticity nabídky (grafy)

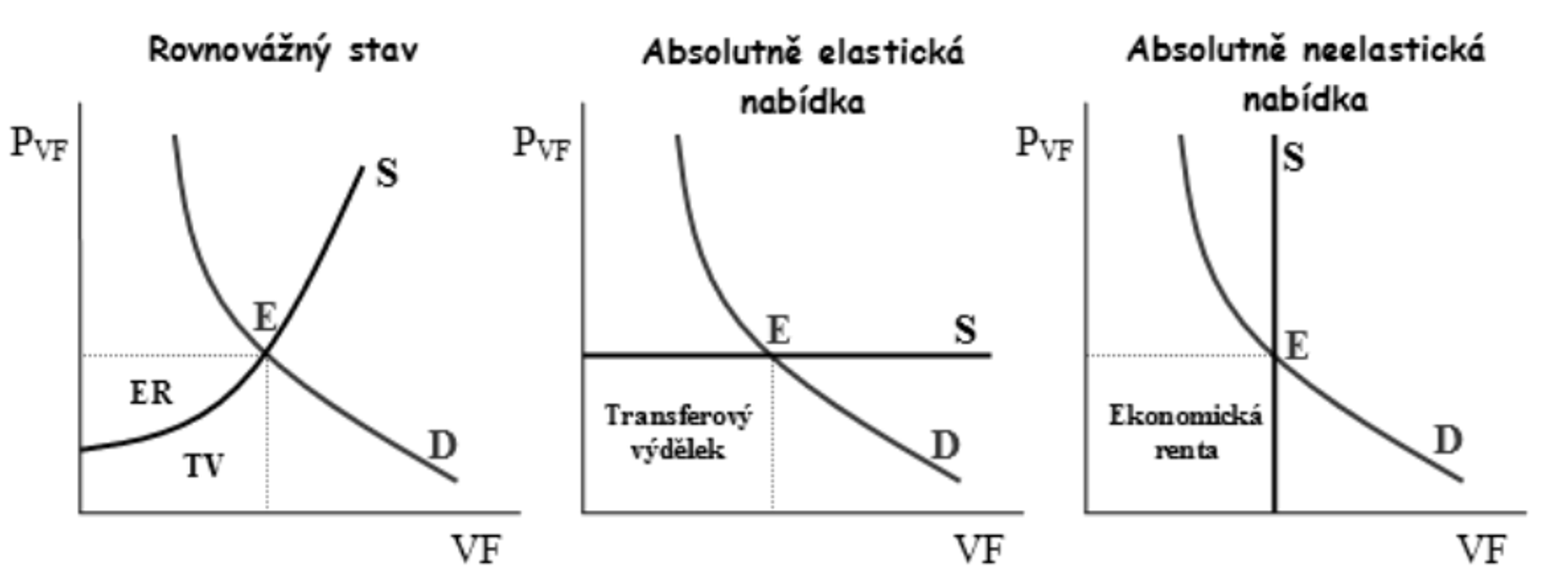
Optimum firmy na trhu výrobních faktorů v dokonalé konkurenci (graf)

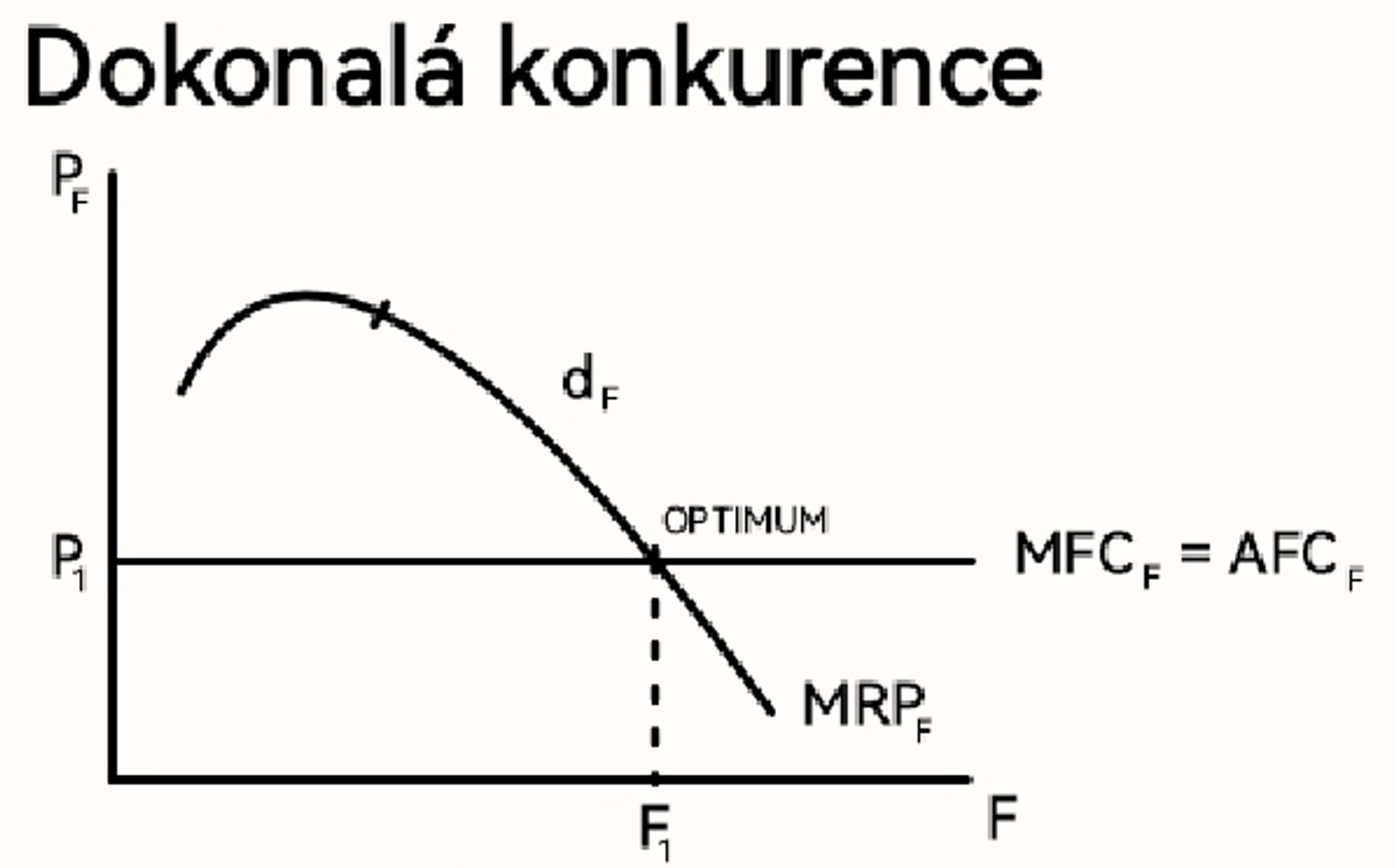
Formy cen výrobních faktorů

• Mzdová sazba → práce w

• Sazba pozemkové renty → půda a

• Úroková míra → kapitál i

Teorie rozdělování na bázi teorie mezní produktivity

Každý výrobní faktor dostává odměnu podle svého příspěvku k výrobnímu procesu.

MP_F=MC_F, například MP_L=w

Skladba důchodů domácností (definice, vzorec)

Celkové množství peněz, které domácnost obdrží během určitého časového období (Y)

• Pracovní důchody YL

• Důchody plynoucí z vlastnické půdy YA a kapitálu YK

• Důchod ve formě transferové platby YT

Y=w⋅L+I⋅A+v⋅K+YT

Pracovní důchody domácnosti

YL=w\cdot L (průměrná hodinová mzdová sazba * počet hodin práce)

Důchody domácnosti plynoucí z vlastnické půdy a kapitálu

• Půda: YA = I \cdot A (průměrná míra výnosů z půdy * množství půdy ve vlastnictví)

• Kapitál: YK = v \cdot K (průměrná míra výnosu z kapitálu objem kapitálu ve vlastnictví)

Zdroje nerovností v důchodech lidí

Nerovnost v pracovních důchodech: rozdíly ve schopnostech lidí

Nerovnost ve vlastnických důchodech: rozdíly v tom, co lidi vlastní