PSAT MATH (not supah accurate)

Preliminary Scholastic Assessment Test

Product

The result of multiplication

Quadratic expression

ax²+bx+c

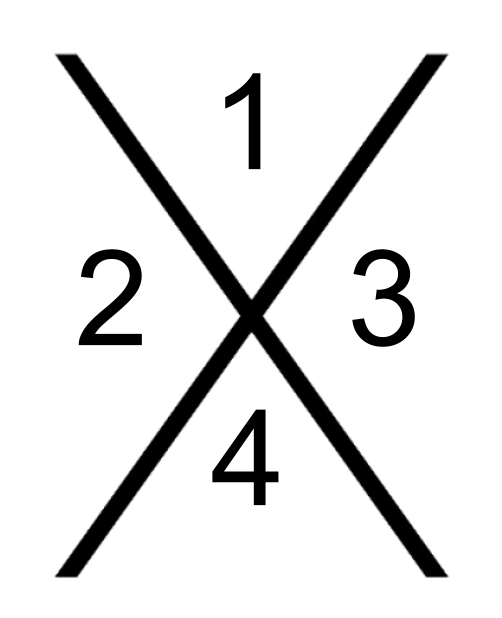
Factoring quadratics: What does #1 represent in the Diamond Method?

The product of a and c

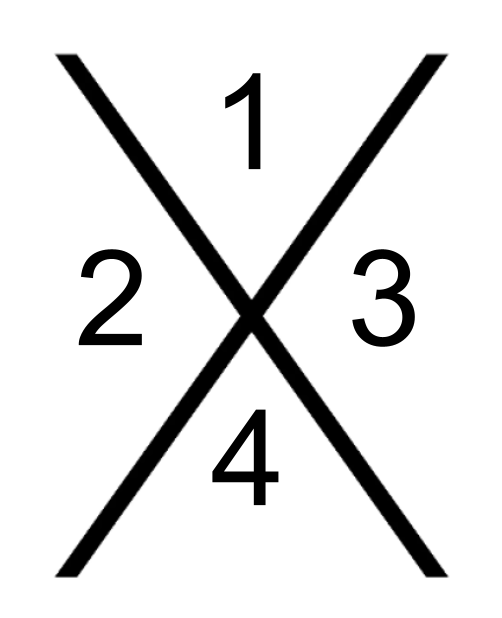
Factoring quadratics: What do #2 and #3 represent in the Diamond Method?

2 factors that are both the product of a and c, and have the sum of the b value

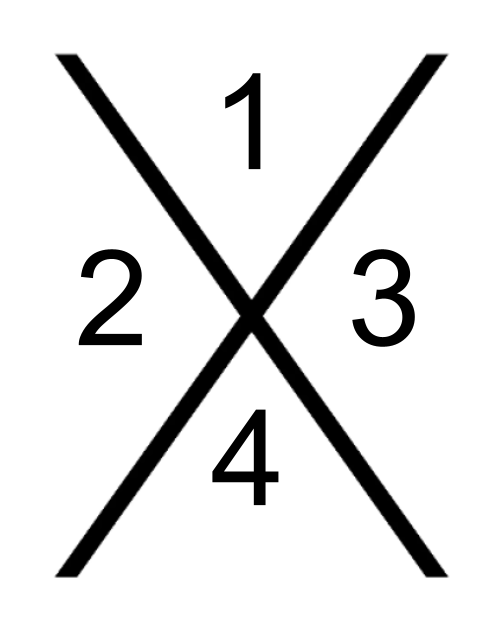
Factoring quadratics: What does #4 represent in the Diamond Method?

B value

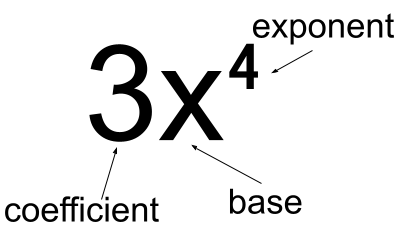
Radicals and rational exponents: Exponential exponents

Algebraic expressions with a base and exponents (as well as coefficients if it contains variables)

Radicals and rational exponents: Fractional exponents

Exponents that can be represented as fractions and radicals.

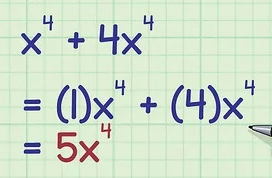
Rules of exponent operations: Adding and subtracting expressions

We can only combine variables if they have the same base and exponent.

Rules of exponent operations: Multiplying exponential expressions

We keep the base, multiply coefficients and add exponents.

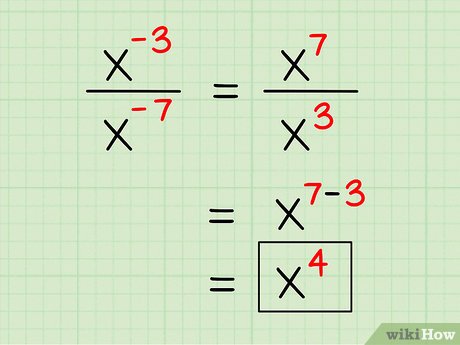
Rules of exponent operations: Dividing exponential expressions

We keep the base, divide coefficients and subtract exponents.

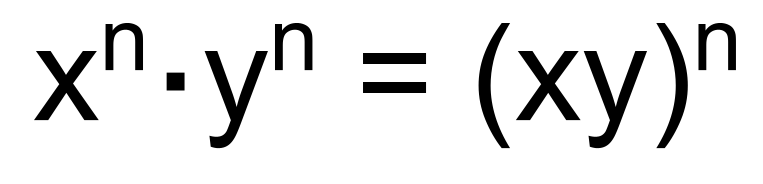
Rules of exponent operations: Multiplying with different bases.

We keep the exponents the same

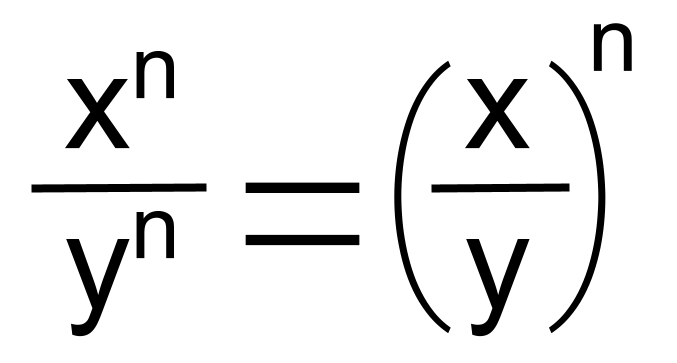
Rules of exponent operations: Divide with different bases

We divide the bases and keep the exponents the same

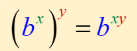
Rules of exponent operations: Raising an exponential expression to an exponent

We keep the base the same and multiply the two exponents

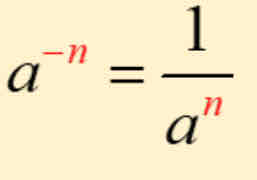
Rules of exponent operations: Negative exponents

A base raised to a negative exponent is equivalent to 1 divided by the base (raised to the opposite of the exponent)

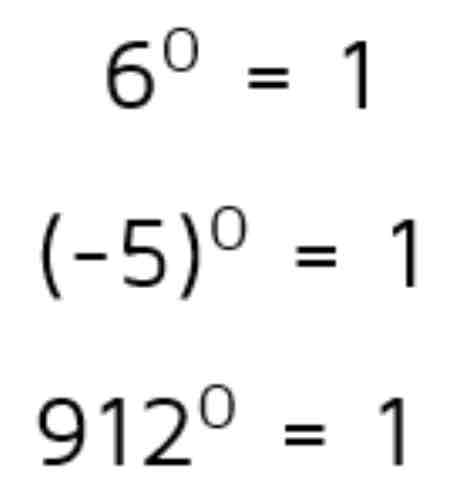
Rules of exponent operations: zero exponent

When a base is raised to an exponent of 0, it is equal to 1

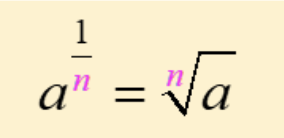
Roots and rational exponents: The basics

When we rewrite a fractional exponent as a radicle, the exponent undeer the radical is the numerator and the number to the left is the denominator.

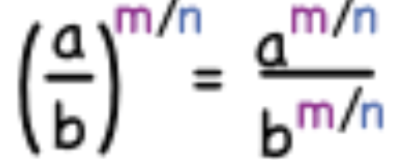
Roots and rational exponents: Division

When dividing two rational exponents by each other, we can simplify and place them under the radical.

Rational expressions: How to solve

Factor it out into (x-a)(x+b) form, then divide or multiply the remaining numerators and denominators.

Nonlinear functions: How to solve

Plug in three input values and run them by the function to create the graph.

Composing function: What even is this

Identify inner and outer functions, write the outer function, and substitute each x with the inner function.

Quadratic Formula when ax²+bx+c=0

x = (b ± √b²-4ac)/(2a)

Is 2² = (-2)²

Yes

The formula for population growth and decline is:

P(t)=P₀r^t

The formula for compounding interest is:

P(t)=P₀(1+r)^t

When we calculate population growth, P₀ is

the initial population (when t=0)

When we calculate population growth, t is

the input variable that represents the time elapsed

When we calculate population growth, if r is greater than 1, the population is

growing

When we calculate population decline, if r is less than 1, the population is

declining

When we calculate compounding interest, P₀ is

initial amount of money

When we calculate compounding interest, t is

the input variable representing the time elapsed

When we calculate compounding interest, r is

the interest rate for each time period (is a decimal)

For parabolas, when the a in ax2+bx+c=0 is less than 0, the parabola opens

downward

For parabolas, when the a in ax2+bx+c=0 is more than 0, the parabola opens

upward

For parabolas, the y-intercept is equal to

(0,c)

For parabolas, the vertex is its

lowest or highest point

For parabolas, we can calculate the x-coordinate of the vertex using the formula

(-b)/(2a)

For parabolas, when they are in the factored for y = (x-b)(x-c), the x-intercepts are

(b, 0) (c,0)

Weird sigmoid/S-shape graphs: f(x)=(x-a)(x-b)(x-c) What is a’s relationship?

If a>0, y approaches positive infinity. If a<0, y approaches negative infinity.

Weird sigmoid/S-shape graphs: f(x)=(x-a)(x-b)(x-c) What are the x-intercepts?

(a,0) (b,0) (c,0)

What is a traversal?

A line that intersects a system of lines

Reflection over the x-axis

(x,-y)

Reflection over the y-axis

(-x,y)

Reflection over y=x

(y,x)

Reflection over y=-x

(-y,-x)

Rotation by 90 degrees clockwise + 270 degrees counterclockwise

(y,-x)

Rotation by 90 degrees counterclockwise + 270 degrees clockwise

(-y,x)

Rotation by 180 degrees

(-x,-y)

The SOH is SOHCAHTOA stands for

Sine equals Opposite over Hypotenuse

The CAH in SOCAHTOA is

Cosine equals Adjacent over Hypotenuse

The TOA in SOHCAHTOA is

Tangent equals Opposite over Adjacent