Geometry Theorems/Postulates/Laws

Things you need to write for Geometry proofs/ things I need to know to pass geometry.

Law of Detachment

If the hypothesis of a true conditional statement is true, then the conclusion is also true

Law of Syllogism

If hypothesis p, then conclusion q. If hypothesis q, conclusion r. If these statements are true, then you get rid of q and add those two together.

Two Point Postulate

Through any two points, there exist exactly one line

Line-Point Postulate

A line contains at least two points

Line Intersection Postulate

If two lines intersect, then their intersection is exactly one point.

Three Point Postulate

through any three non-collinear points, there exists exactly one plane.

Plane-Point Postulate

A plane contains at least non-collinear points

Plane-Line Postulate

If two points lie in a plane, then the line containing them lies in the plane

Plane Intersection Postulate

If two planes intersect, then their intersection is a line.

Right Angles Congruence Theorem

All right angles are congruent

Congruent Supplement Theorem

If two angles are supplementary to the same angle(or to congruent angles), then they are congruent.

Congruent Complement Theorem

If two angles are complementary to the same angle (or to congruent angles), then they are congruent.

Linear Pair Postulate

If two angles form a linear pair, then they are supplementary.

Vertical Angles Congruence Theorem

Vertical angles are congruent.

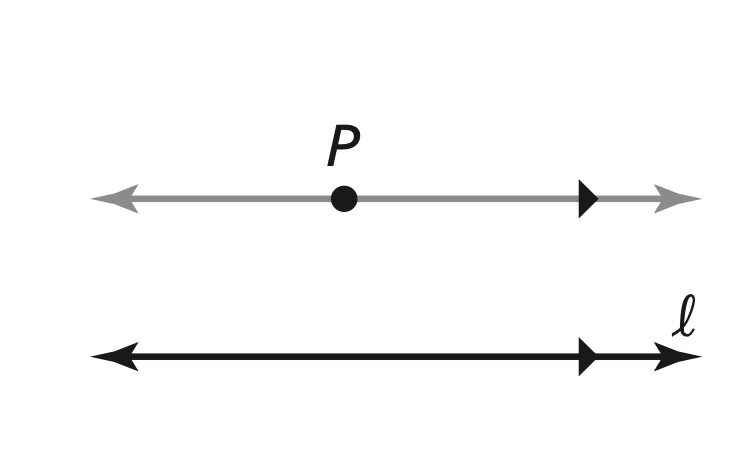
Parallel Postulate

If there is a line and a point not on the line, then there is exactly one line through the point parallel to the given line.

There is exactly one line through P parallel to l.

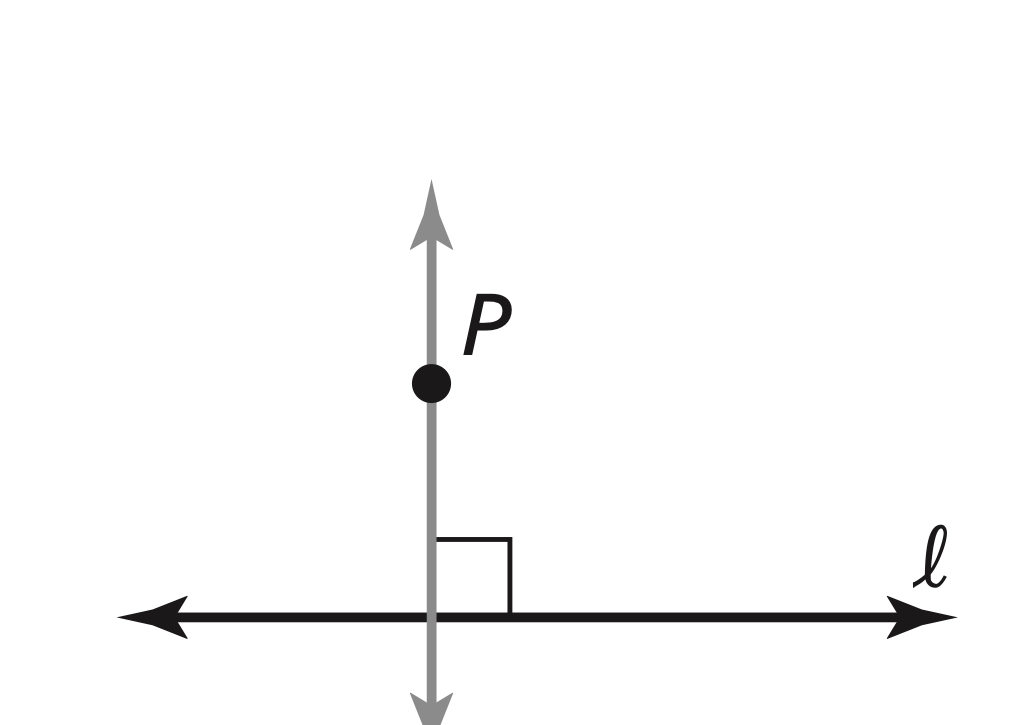
Perpendicular Postulate

If there is a line and a point not on the line, then there is exactly one line through the point perpendicular to the given line.

There is exactly one line through P perpendicular to l.

Corresponding Angles Theorem

If two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent.

Alternate Interior Angles Theorem

If two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent.

Alternate Exterior Angles Theorem

If two parallel lines are cut by a transversal, then the pairs of alternate exterior angles are congruent.

Consecutive Interior Angles Theorem

If two parallel lines are cut by a transversal, then the pairs of conservative interior angles are supplementary.

Alternate Interior Angles Converse

If two lines are cut by a transversal so the alternate interior angles are congruent, then the lines are parallel.

Alternate Exterior Angles Converse

If two lines are cut by a transversal so the alternate exterior are congruent, then the lines are parallel.

Consecutive Interior Angles Converse

If two lines are cut by a transversal so the consecutive interior angles are supplementary, then the lines are parallel.

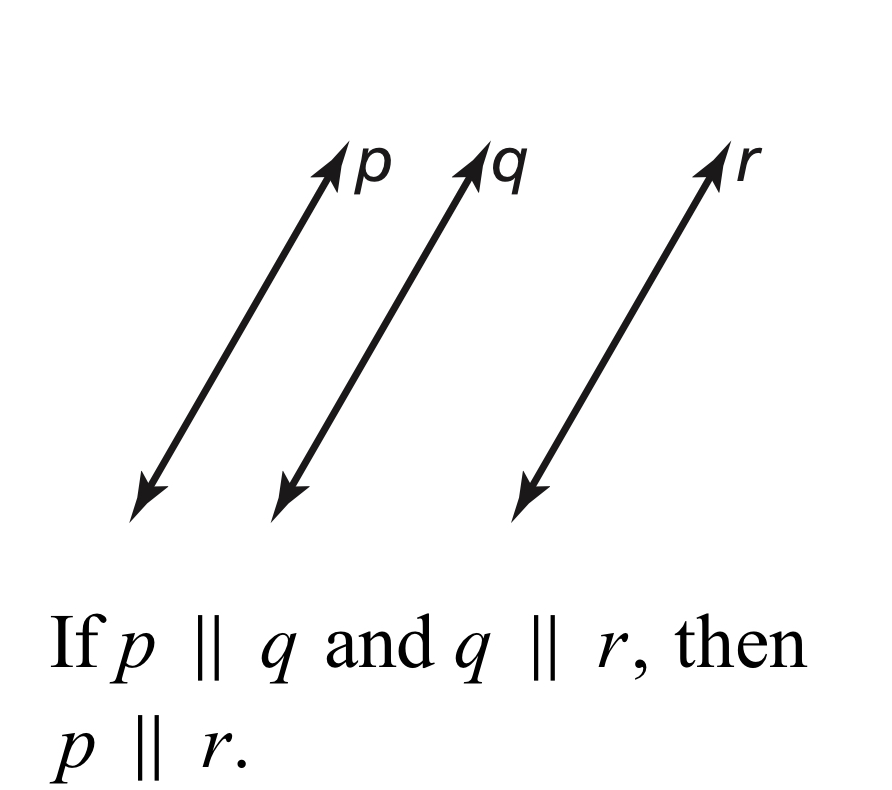
Transitive Property of Parallel Lines Theorem

If two lines are parallel to the same line, then they are parallel to each other

Linear Pair Perpendicular Theorem

If two lines intersect to form a linear pair of congruent angles, then the lines are perpendicular.

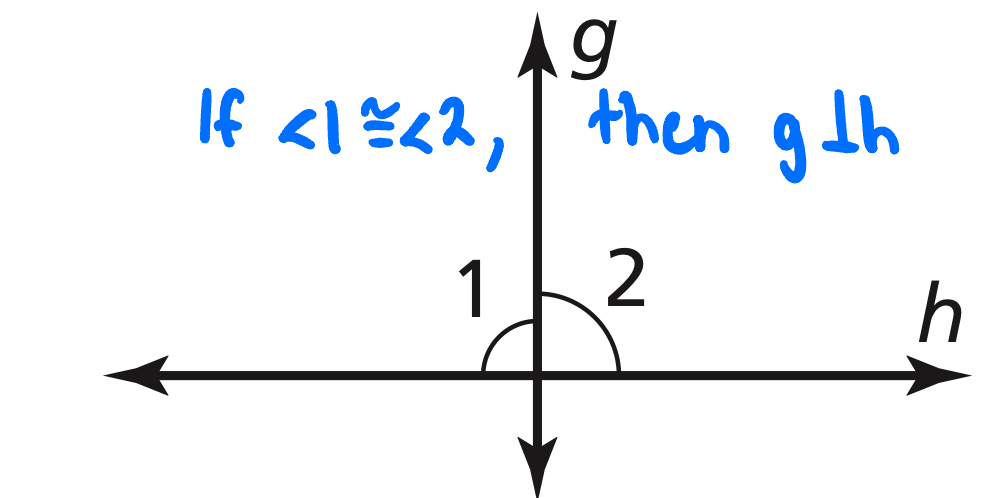
Perpendicular Transversal Theorem

If a plane, if a transversal is perpendicular to one of two parallel lines, then it is perpendicular to the other line.

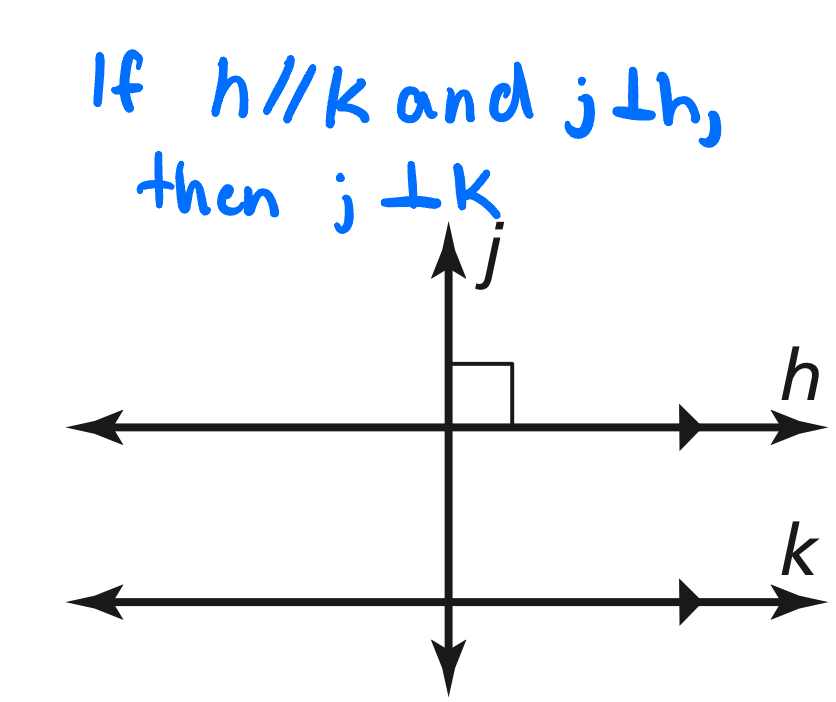
Lines Perpendicular to a Transversal Theorem

In a plane, if two lines are perpendicular to the same line, then they are parallel to each other.

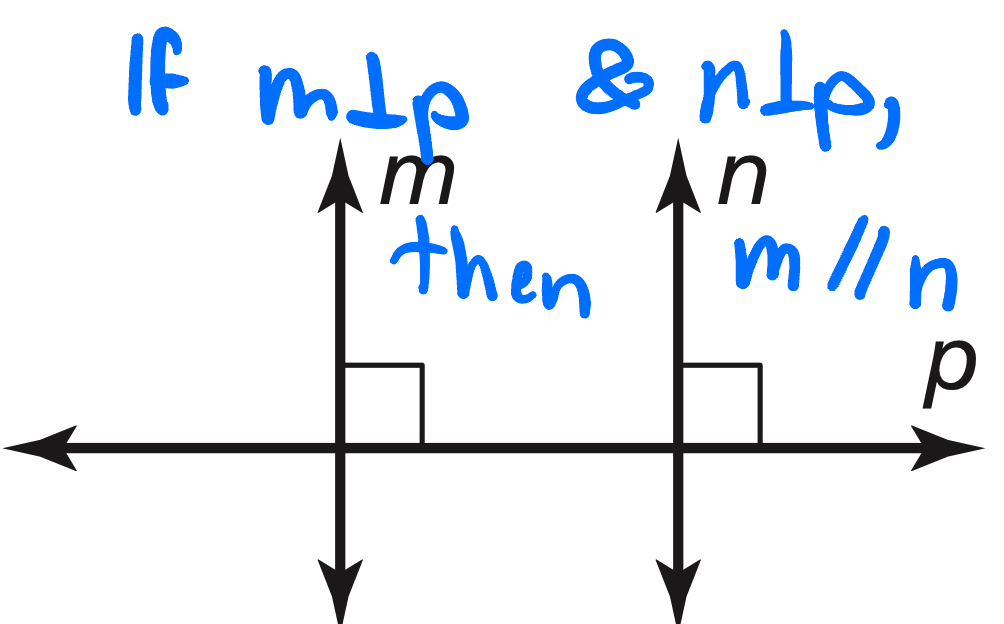
Slopes of Parallel Lines Theorem

In a coordinate plane, two non-vertical lines are parallel if and only if they have the same slope

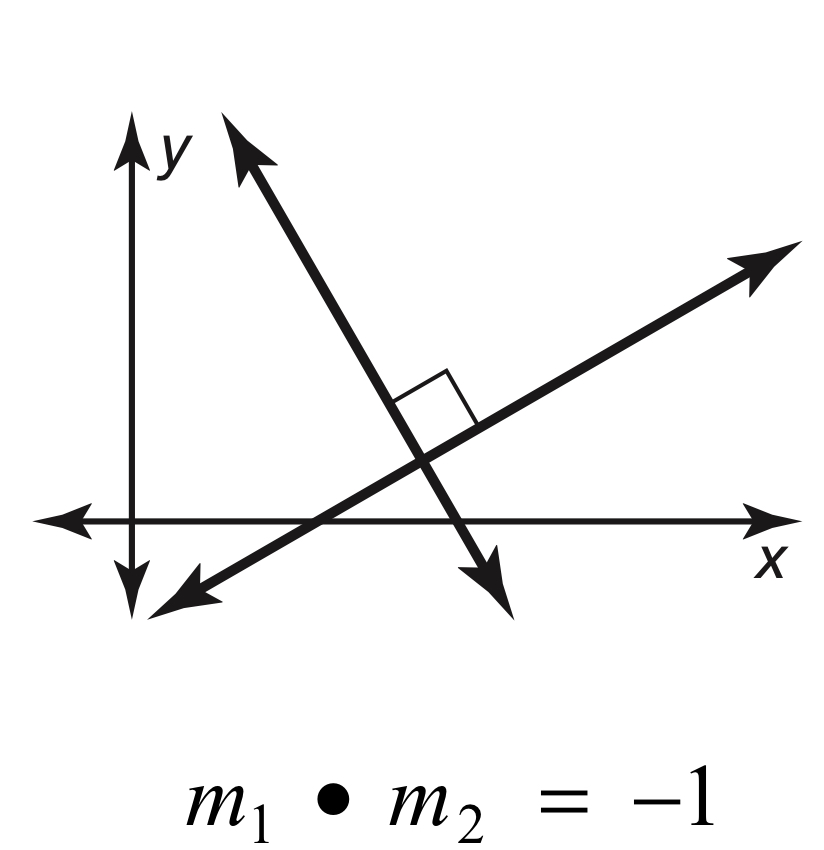
Slopes of Perpendicular Lines Theorem

In a coordinate plane, two non-vertical lines are perpendicular if and only if the product of their slopes is -1

Reflections in Parallel Lines Theorem

If lines k and m are parallel, then a reflection in line k followed by a reflection in line m in the same as a translation.

If A” is the image of A’, then

1. AA” is perpendicular to k and m, and AA”=2d, where d is the distance between k and m.

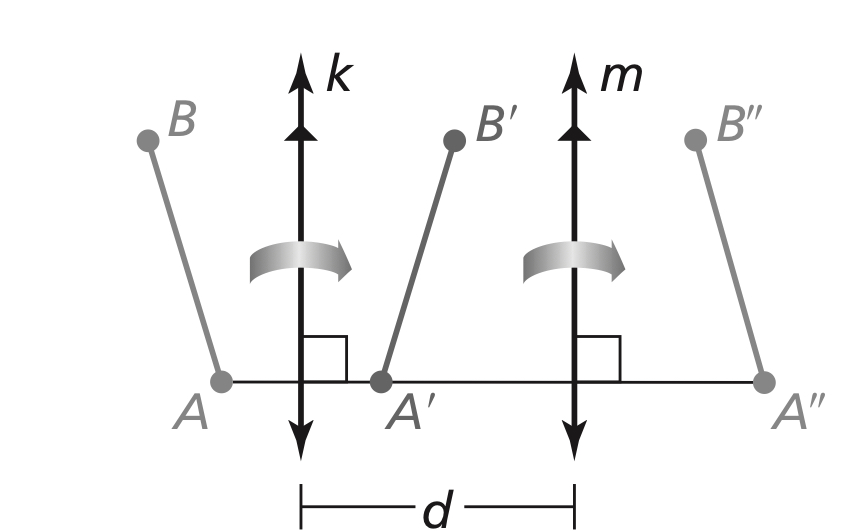
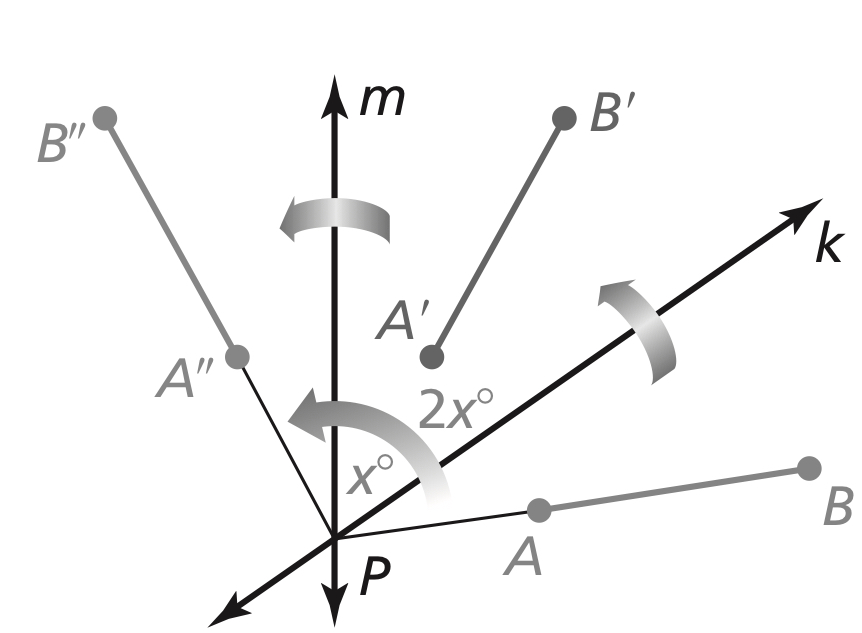
Reflection in Intersecting Lines Theorem

If lines k and m intersect at point P, then a reflection in line k followed by a reflection in line m is the same as a rotation about point P.

The angles of rotations is 2x^o, where x^o is the measure of the acute or right angle formed by lines k and m

Triangle Sum Theorem

The sum of the measures of the interior angles of a triangles is 180^o

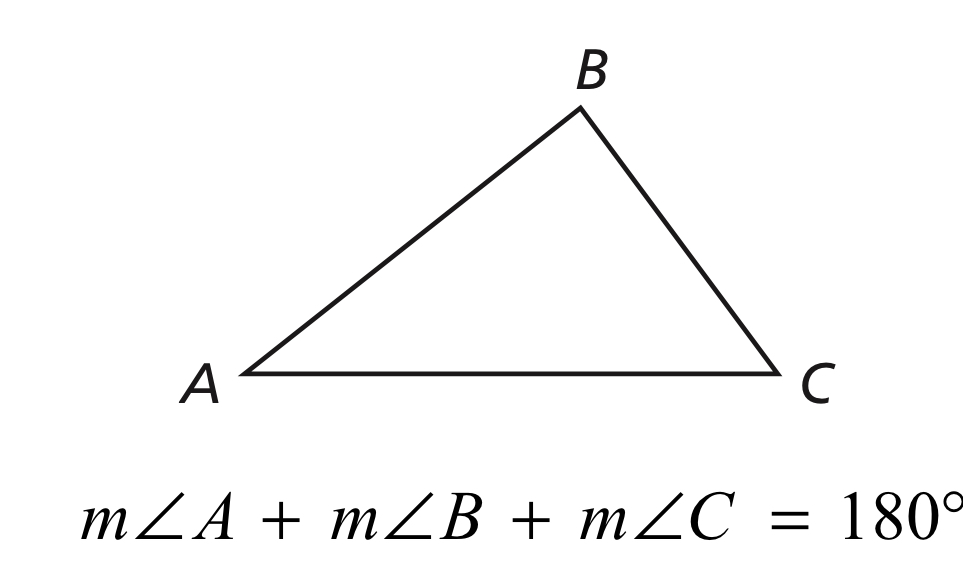
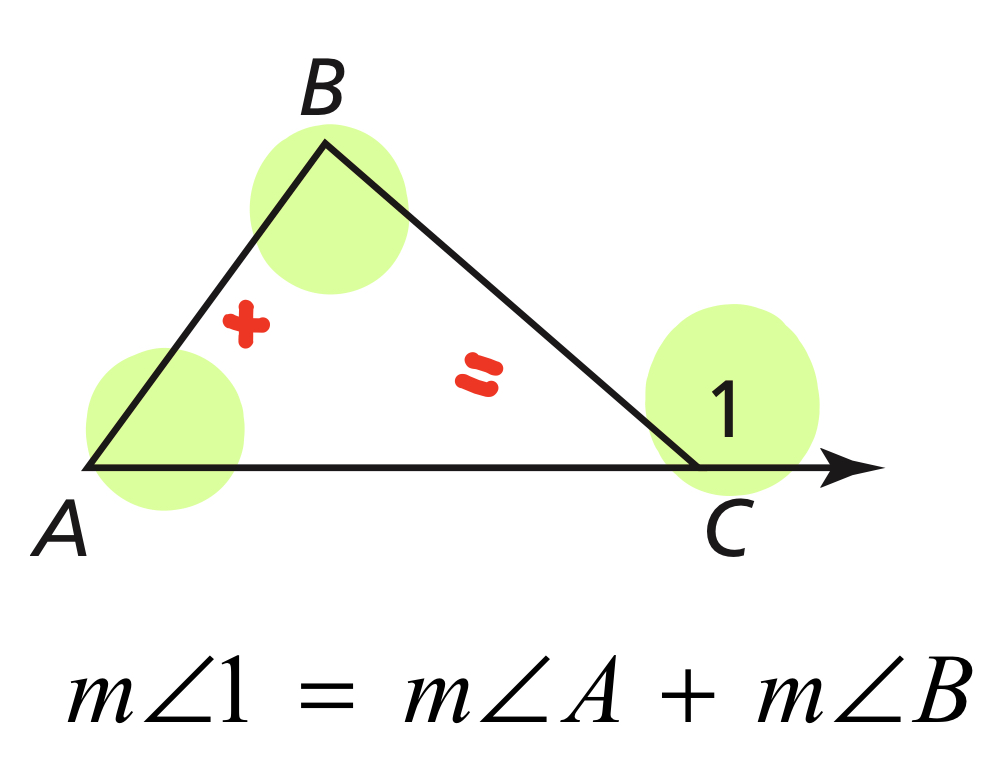
Exterior Angle Theorem

The measure of an exterior angles of a triangle is equal to the sum of the measure of the two non-adjacent interior angles.

Corollary to the Triangle Sum Theorem

The acute angles of a right triangle are complementary.

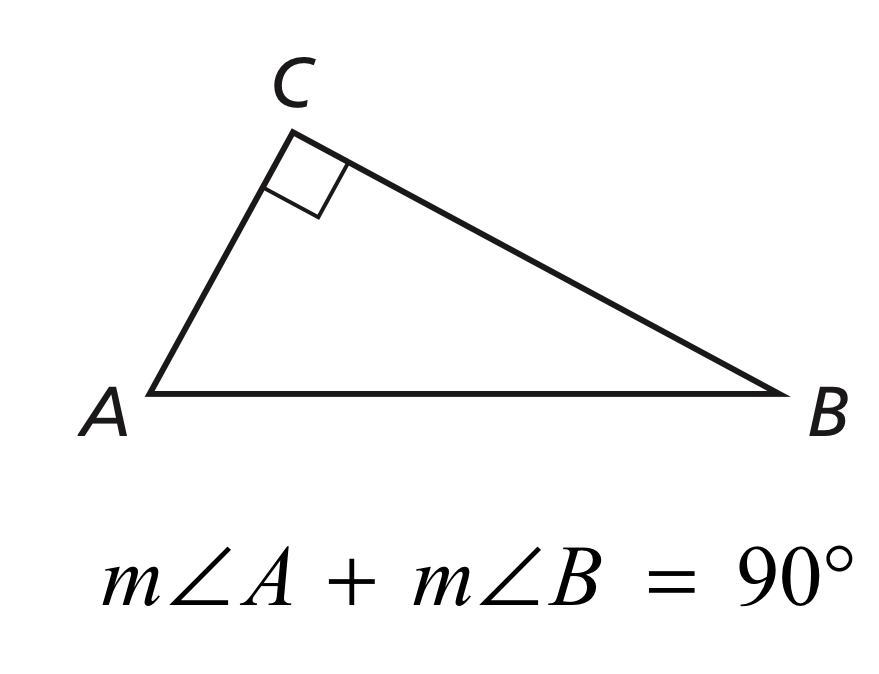
Third Angles Theorem

If two angles of one triangles are congruent to two angles of another triangle, then the third angles are also congruent.

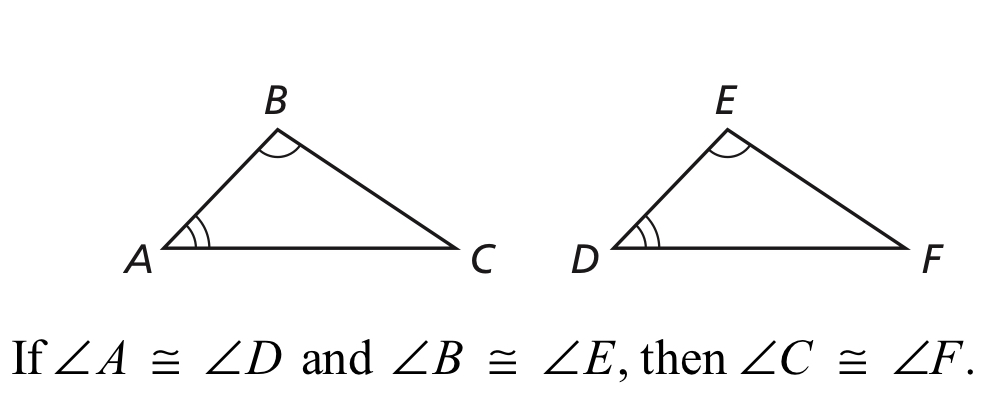
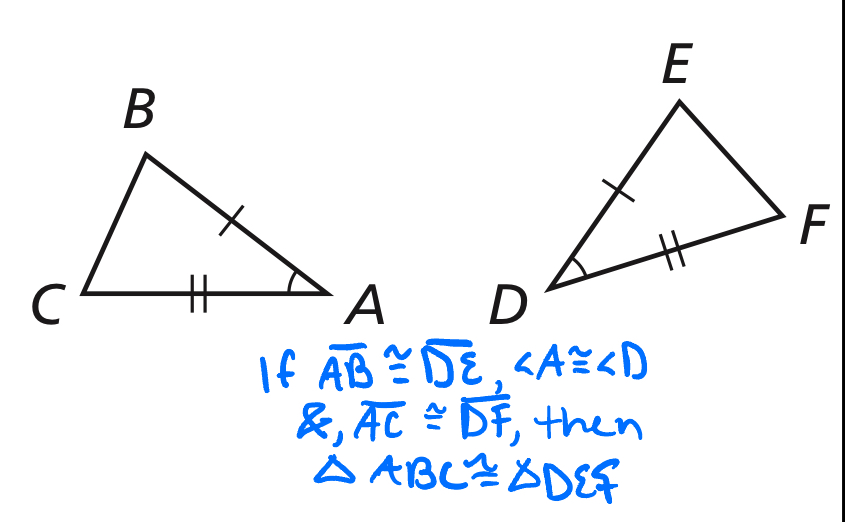
Side-Angle-Side (SAS) Congruence Theorem

If two sides and the included angles of one triangle are congruent to two sides and the included angles of a second triangle, then the two triangles are congruent.