Geometry

What are vectors in R^n, common norms/distances, and what is the scalar product used for?

• A vector is just a point/arrow in R^n, written as coordinates:

x = (x1, x2, ..., xn)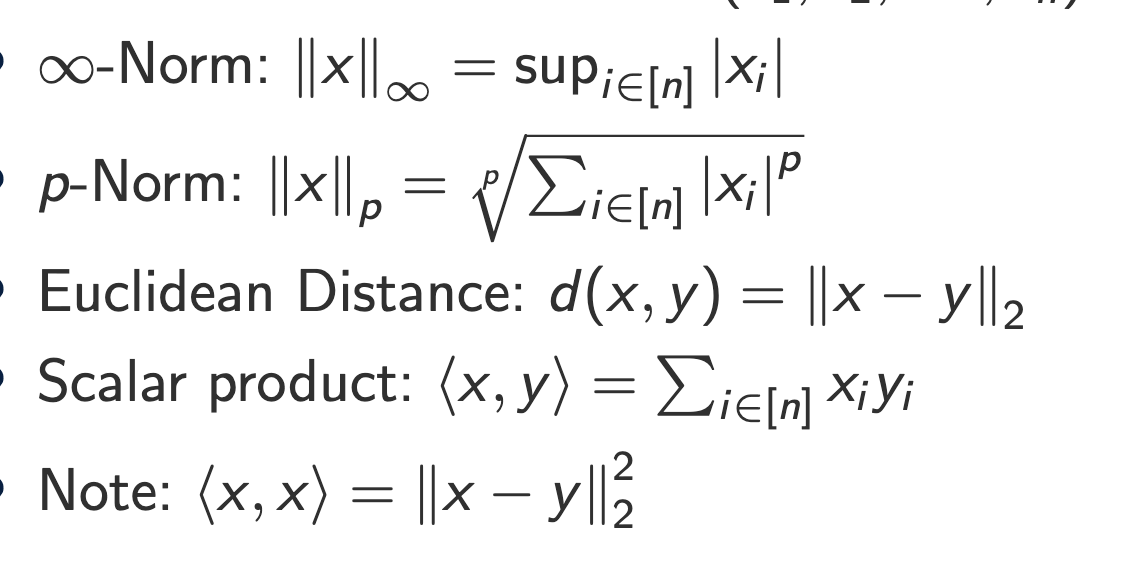

• Infinity norm (max absolute coordinate):

Example: x=(2,-5,1) ⇒ ||x||∞ = 5.

• p-norm (general norm)

Example with p=2: x=(3,4) ⇒ ||x||2 = sqrt(3^2+4^2)=5.

• Euclidean distance between two points x,y:

d(x,y) = ||x-y||2

Example: x=(1,2), y=(4,6) ⇒ x-y=(-3,-4) ⇒ distance =5

How do you test perpendicularity and how can you construct perpendicular vectors in R^2 and R^3?

What are linear and convex combinations?

What does the determinant tell us geometrically?

When do two vectors lie on the same line through the origin?

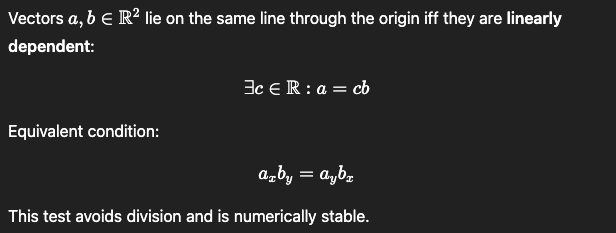
first Vector_x * second Vector_y = first Vector_y * second Vector_x

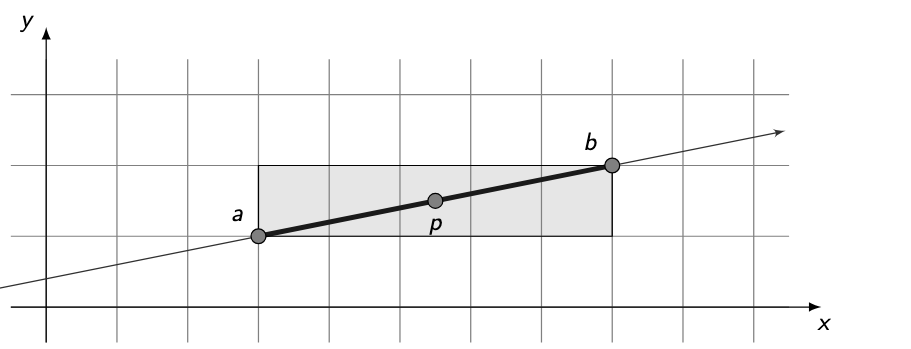
How do you test whether a point lies on a given line?

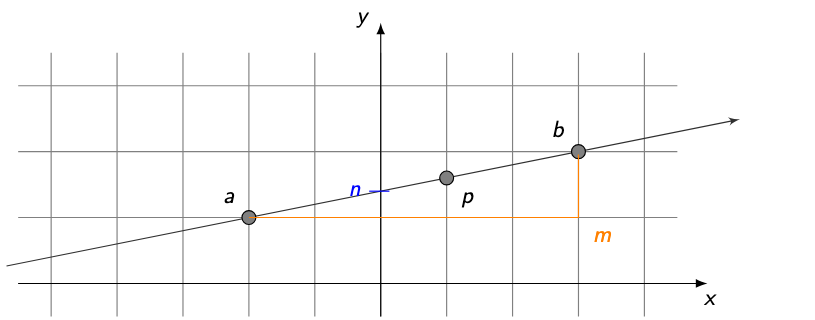
A point p lies on the line through a and b if vectors:

p − a   and   b − a

are linearly dependent. (first Vector_x * second Vector_y = first Vector_y * second Vector_x)

In 2D, the condition is:

(px − ax)(by − ay) = (py − ay)(bx − ax)

Interpretation:

• Both vectors point in the same direction → p is on the line

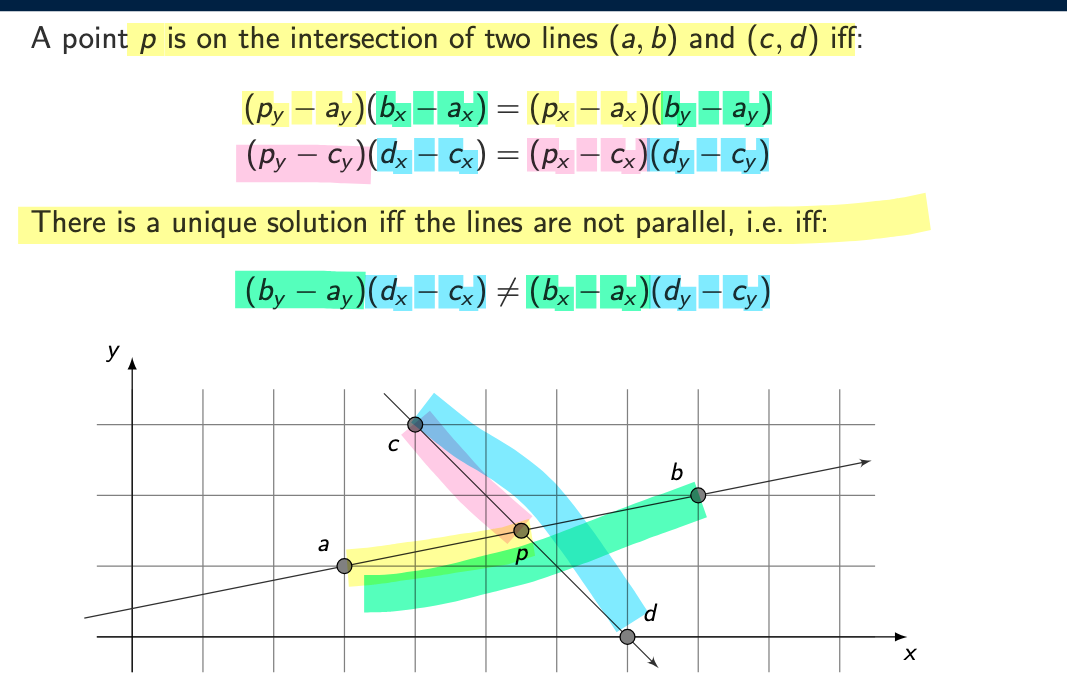
When do two lines intersect, and when is the intersection unique?

How do you check if a point is on a line segment?

Two steps:

1. Check if the point is on the infinite line

2. Check if it lies between the endpoints

Condition:

px is between ax and bx
py is between ay and by

Both x and y must be within bounds.

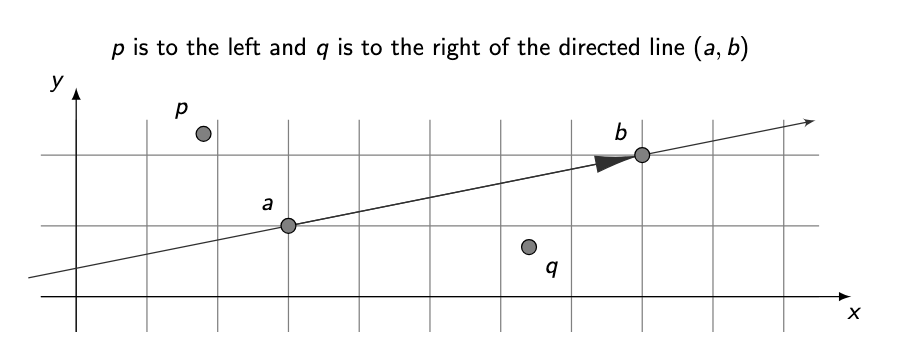
How do we decide if a point is left, right, or on a directed line?

We use the counter-clockwise (CCW) function:

CCW(a, b, p) = (py − ay)(bx − ax) − (px − ax)(by − ay)

Interpretation:

• CCW = 0 → point is on the line

• CCW > 0 → point is left of the line

• CCW < 0 → point is right of the line

det(CCW) / 2 = area of triangle (a, b, p)

What is a polygon, and what does “simple polygon” mean?

A polygon is a closed shape made of straight line segments.

A polygon is simple if:

• Edges do not intersect somewhere in the middle,( except at shared endpoints.)

What is the point-in-polygon problem?

Given a polygon and a point q, is q inside or outside the polygon?

This is a very common geometry problem, for example in graphics and collision detection.

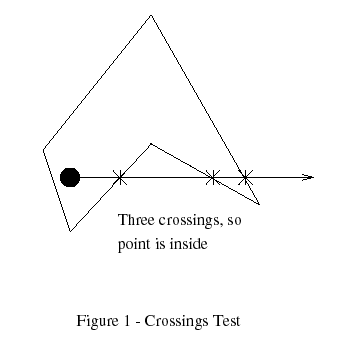
We solve it using the ray casting algorithm.

Idea:

• From point q, cast a ray (half-line) in any direction

• Count how many times the ray intersects polygon edges

Decision rule:

• Odd number of intersections → point is inside

• Even number of intersections → point is outside

Why it works:

• Every time we cross the boundary, we switch between inside and outside

Important:

• Direction does not matter, as long as it doesn’t go exactly through vertices

What special cases must be handled in the ray casting algorithm?

wo important issues:

1. Ray hits a vertex

   • Hard to define if it counts as 1 or 2 intersections

   • Simple solution: change ray direction

2. Floating-point precision

   • Point may be very close to an edge

   • Use tolerances (epsilon) in comparisons

How can we compute the area of a polygon?

We compute the area by splitting the polygon into triangles.

Key facts:

• Works only if vertices are in order

• If order is counter-clockwise, area is positive

• If clockwise, area is negative (signed area)

What is the center of mass in geometry? What is the center of mass of a triangle or polygon?

The center of mass (COM) is the average position of all points in a shape.

Intuition:

• If the object were made of uniform material,

• the center of mass is where it would balance perfectly.

For geometry problems, we compute it using averaging or area-weighted formulas.

• For a finite set of points:

COM = (sum of all points) / (number of points)

• For a shape with area:

COM = (integral of x over the shape) / (area of the shape)

• If a shape is split into parts:

COM = weighted average of the parts’ COMs

Weight = area of each part.

• For a triangle with vertices a, b, c:

COM = (a + b + c) / 3

• For a simple polygon:

  • Uses a formula based on the shoelace terms

  • Requires vertices in counter-clockwise order

  • Depends on the polygon’s area

For oral exams:
👉 Say that polygon COM is computed by area-weighted averaging of edges.

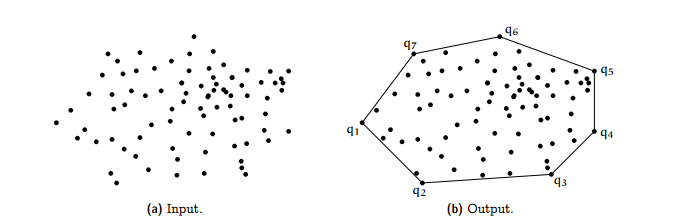
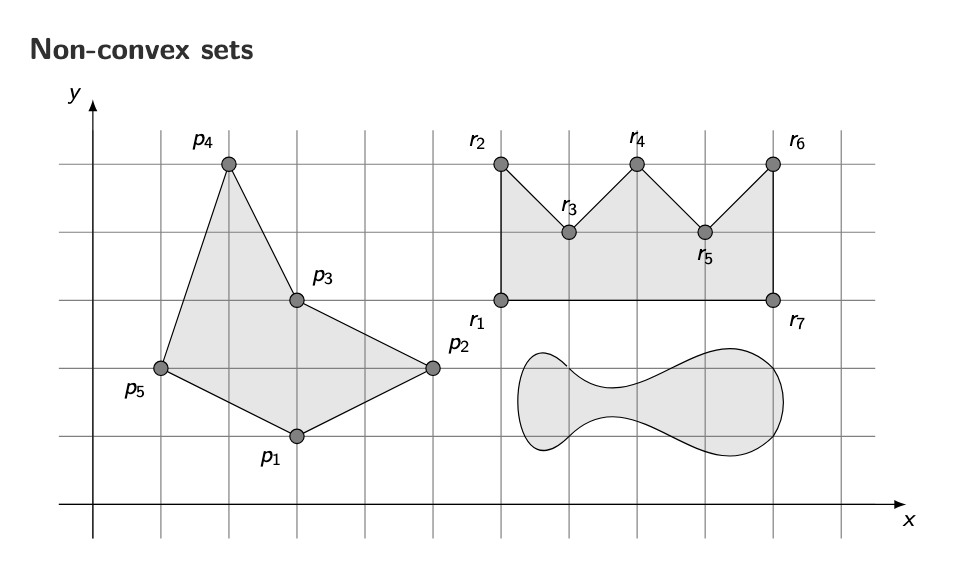
What does it mean for a set to be convex? What is the convex hull of a set of points? When is a polygon convex?

A set is convex if:

• For any two points in the set,

• the entire line segment between them is also inside the set.

Formally:

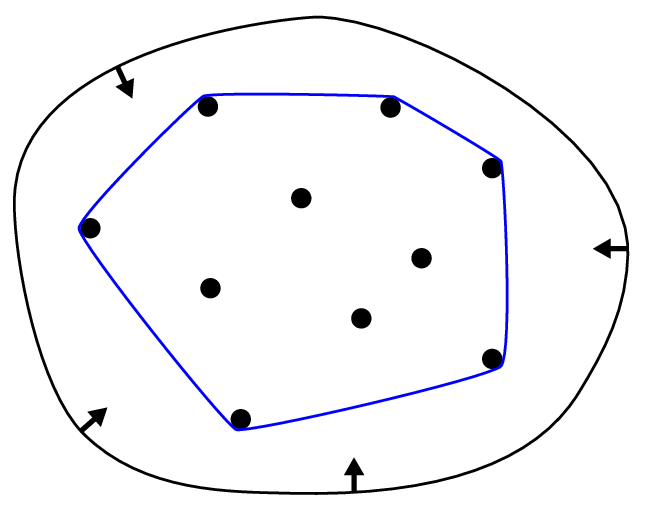
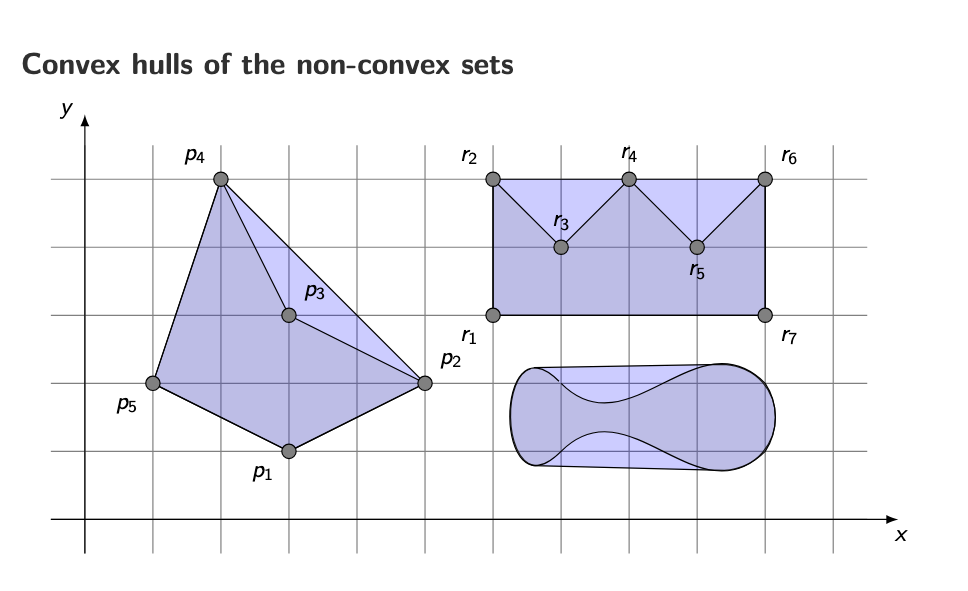
x, y ∈ P  ⇒  [x, y] ⊆ P

The convex hull is:

The smallest convex set that contains all points.

Intuition:

• Imagine stretching a rubber band around the points

• When released, it forms the convex hull

Important facts:

• The convex hull of points is a polygon

• Only outer points become hull vertices

• Inner points are ignored

A polygon is convex if and only if:

• All interior angles are ≤ 180°

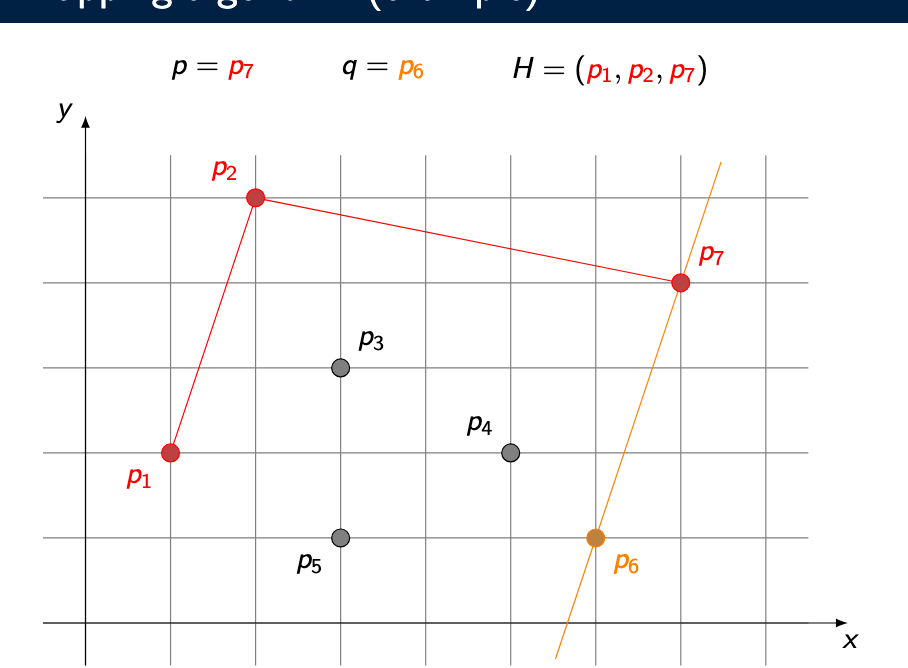
What are the key observations used to find a convex hull? GIFT WRAPPING ALGORITHM

Important ideas:

1. The lexicographically smallest point is always on the convex hull
   (smallest x, then smallest y)

2. An edge (p, q) is a hull edge iff all other points lie on the same side

3. Orientation is tested using CCW

Steps:

1. Pick smallest point p

2. Try all other points q

3. Choose q such that all other points lie on the same side of (p, q)

4. Add q to the hull

5. Repeat until we return to the start

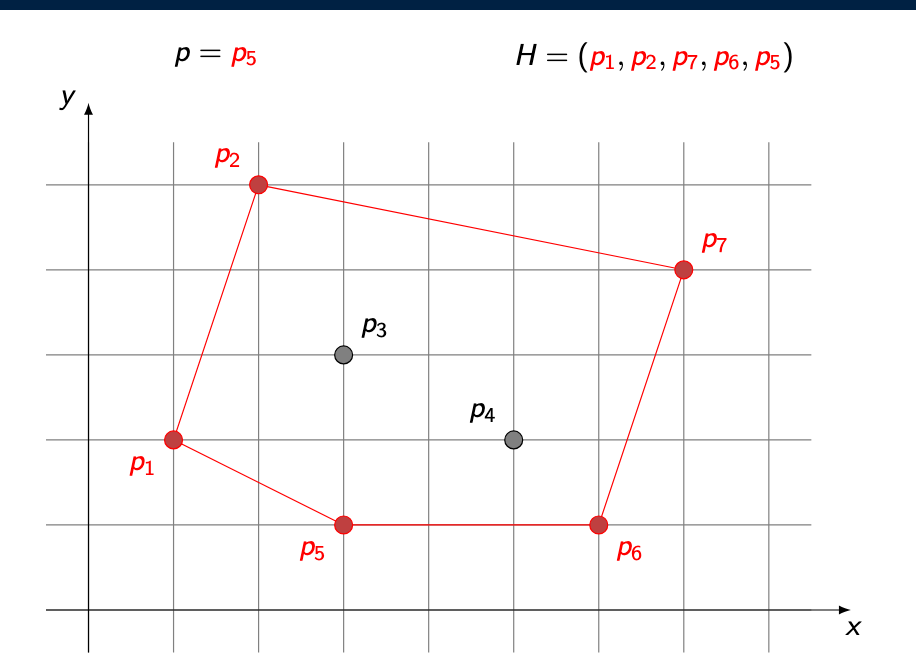
What is the time complexity of the gift-wrapping algorithm?

• Naive implementation:

O(n³)

• Improved version:

O(n²)

• Precise bound:

O(nh)

where:

• n = number of points

• h = number of hull vertices

Good when:

• The hull has few points

What is Graham’s scan used for?

Graham’s scan is an algorithm to compute the convex hull of a finite set of points.

Main idea:

• Pick a starting point on the hull, with smallest x and smallest y

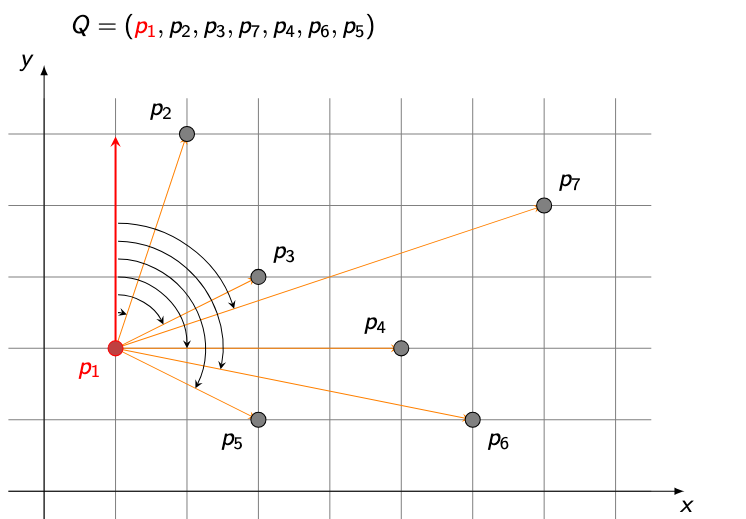
• All points are sorted by the angle they form with the starting point p.

  • Reference direction:

    • Usually the positive y-axis or x-axis

• Start with first two points in the stack

• Move through sorted points:

  • If the path makes a left turn, pop the middle point

  • Continue until a right turn is formed

• Push the current point

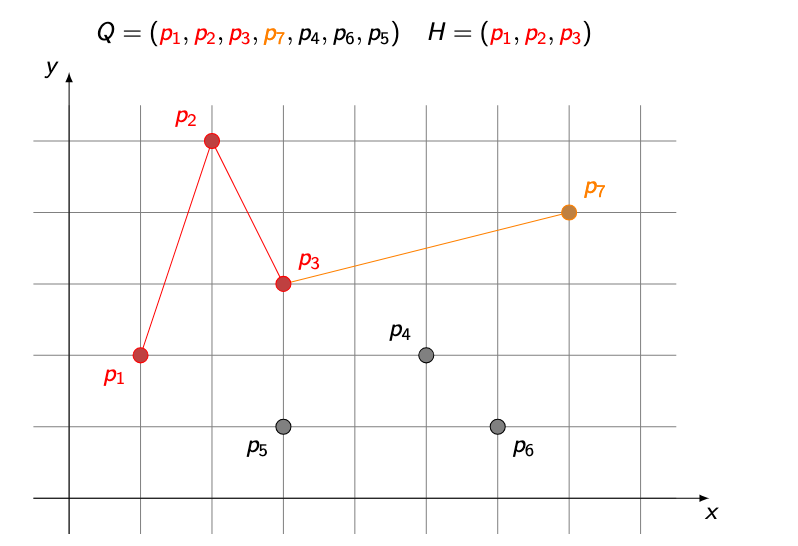
TURN is left (angle at p3 is left) → pop p3, add p7

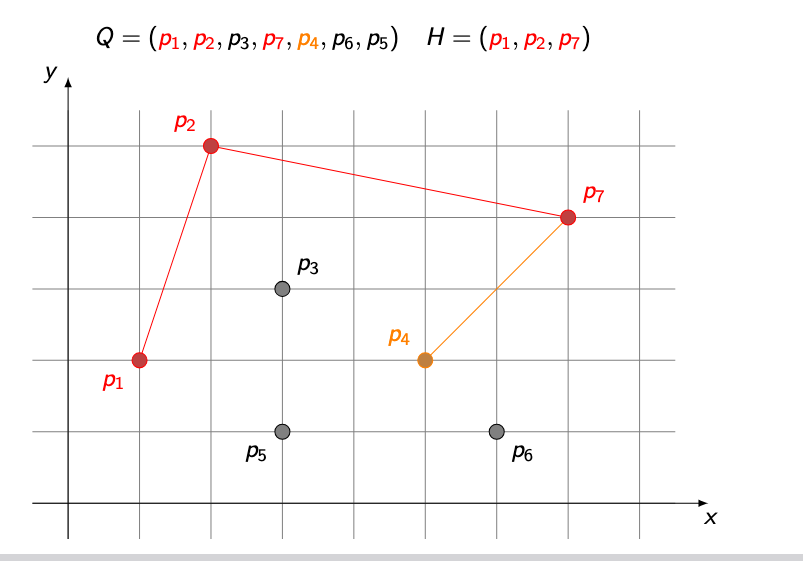
TURN is RIGHT (angle at p7 is right) → continue, add p4

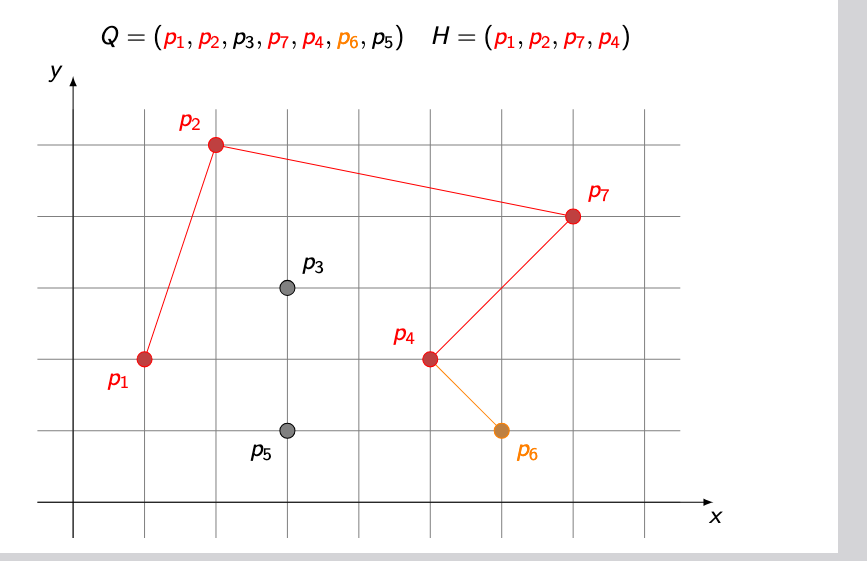
TURN is LEFT (angle at p4 is left) → pop p4 and add p6

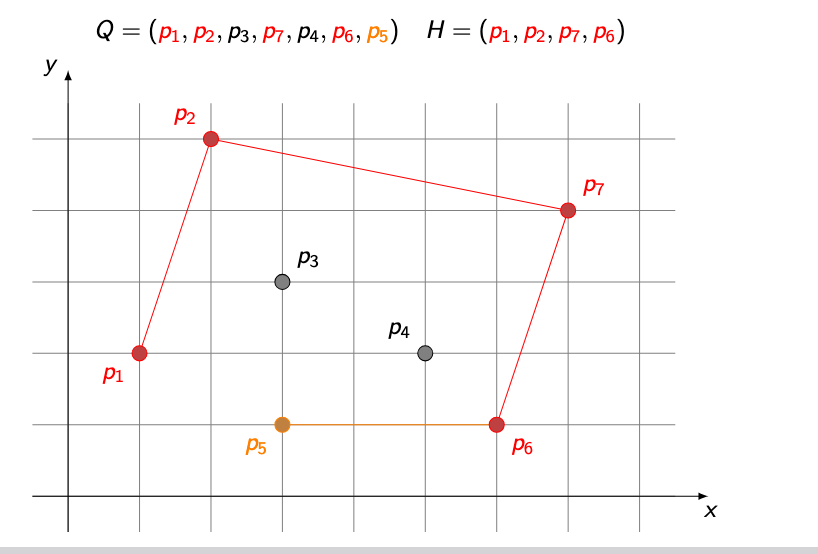
TURN is RIGHT (angle at p6 is right) → continue, add p5

DONE.

It is faster than gift-wrapping for large inputs.

What is the time complexity of Graham’s scan?

What other convex hull algorithms exist, and how do they compare?