Selection Sort

simple sort

Selection Sort

Remove minimum item from input array, add minimum value to sorted array

In-Place Algorithm

Uses little additional space For example, O(1) space

• Find first minimum value

• Move first minimum value to first index (swapping)

• Etc, for second minimum…

In-Place Algorithm Code

class SelectionSort {
   static void selectionSort(int[] array) {
      for (int i = 0; i < array.length; i++) {
         int iMin = 1;
         //find index of minimum
         for (int j = i +1; j < array.length; j++) { 
            if (array[j] < array[iMin]) iMin = j;
         }
         //swap array[i] and array [iMin]
         if (iMin != i) {
            int tmp = array[i];
            array[i] = array[iMin];
            array[iMin] = tmp;
         }
      }
   }
}

Correctness Analysis Proof by Induction

• Base step (for 𝑖 = 0, or the first phase): 

  • In the first phase, we find the minimum value (by linear search) and if it is not the first index in the array, we move it to the first index

• Induction step (for 0 ≤ 𝑖 < length − 1): 

  • By the induction hypothesis (holding for phase 𝑖), the first 𝑖 + 1 entries in the (entire) array are sorted and contain the minimum 𝑖 + 1 values

  • During phase 𝑖 + 1, we compute the minimum value in the sub-array from index 𝑖 + 1 to length − 1. By the induction hypothesis, this is the (𝑖 + 2)th minimum value

  • We move that value to the (𝑖 + 1)th index in the array (if it is not already there)

  • As a result, the first minimum 𝑖 + 2 entries of the array are sorted and contain the minimum 𝑖 +2 values

Correctness

• Prove invariant 

• Invariant for 𝑖 = length − 1 implies that the algorithm is correct

Worst-Case Time Complexity

Operation counting: 

• In each phase 𝑖 (for 0 ≤ 𝑖 < length): 

• At most length − 𝑖 comparisons 

• At most O(length − 𝑖) elementary operations

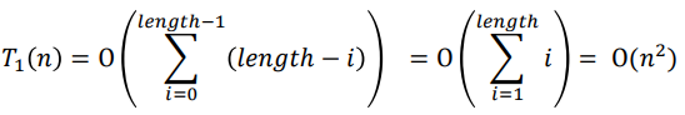
Analysis Summary

• Best case - O(n^2)

• Average case - O(n^2)

• Worst case - O(n^2)

• In-place - yes