pure year 13 content to remember

kill me now im tireddd

when is a mapping a function

if every x value maps to a single y value

how to test if a mapping is function

any vertical line will cross its graph at most once (vertical line test)

what does one-to-one mean

if every y value corresponds to only one x value

what does many to one mean

if some y values come from more than one x value

how to test how many outputs come from an input

horizontal line test

what is the domain of a function

the set of all allowed input values (x values)

what is the range of a function

the set of all possible outputs of a function (y values)

what can f°f(x) also be written as

f²(x)

what is the graph of y=f^-1 (x) like

reflection of the graph y=f(x) in the line y=x

what happens to domain and range with an inverse function

domain of f^-1(x) is same as range of f(x) and the other way round

which type of functions have inverse functions

one-to-one

fg(x) can be written as

f(g(x)) or f°g(x)

when does charging the order of transformations affect the outcome

when two vertical/horizontal transformations are combined

when does charging the order of transformations not affect outcome

one vertical and one horizontal transformations are combined

what is |x-a|<b equivalent to

-b<x-a<b

what is |x-a|>b equivalent to

x-a>b or x-a<-b

what is an increasing sequence

each term is larger than the previous one

what is a decreasing sequence

each term is smaller than the previous one

what is a periodic sequence

where terms start repeating after a while

how to prove a sequence is increasing

u_n+1 - u_n >0 then u_n+1 > u_n

hwo to prove a sequence is decreasing

if u_n+1 - u_n < 0 then u_n+1< u_n

how to find limit L of a convergent sequence

set u_n+1 = u_n = L and solve

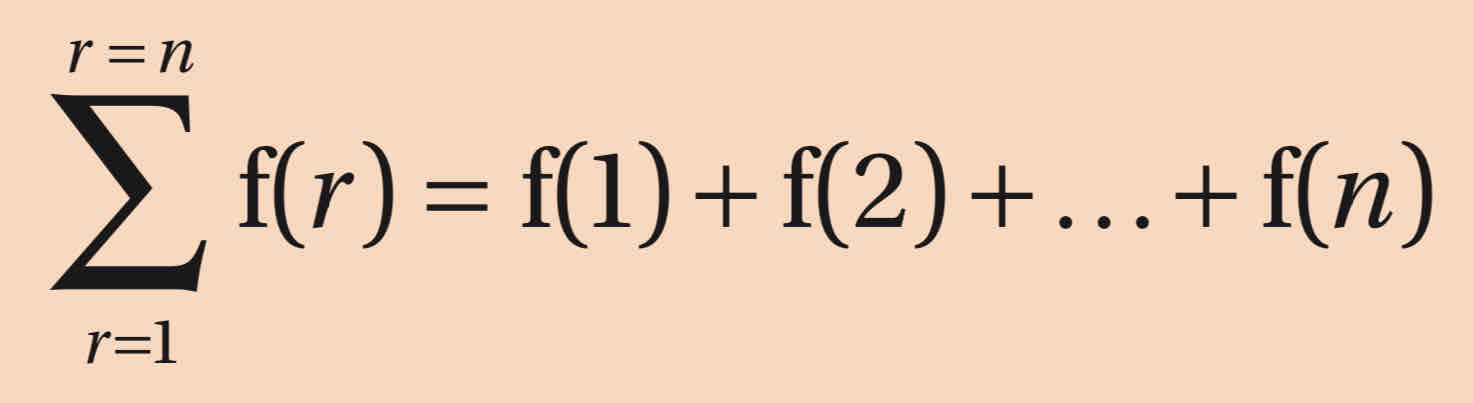
what r mean in sigma notation

a placeholder - shows what changes with each new term

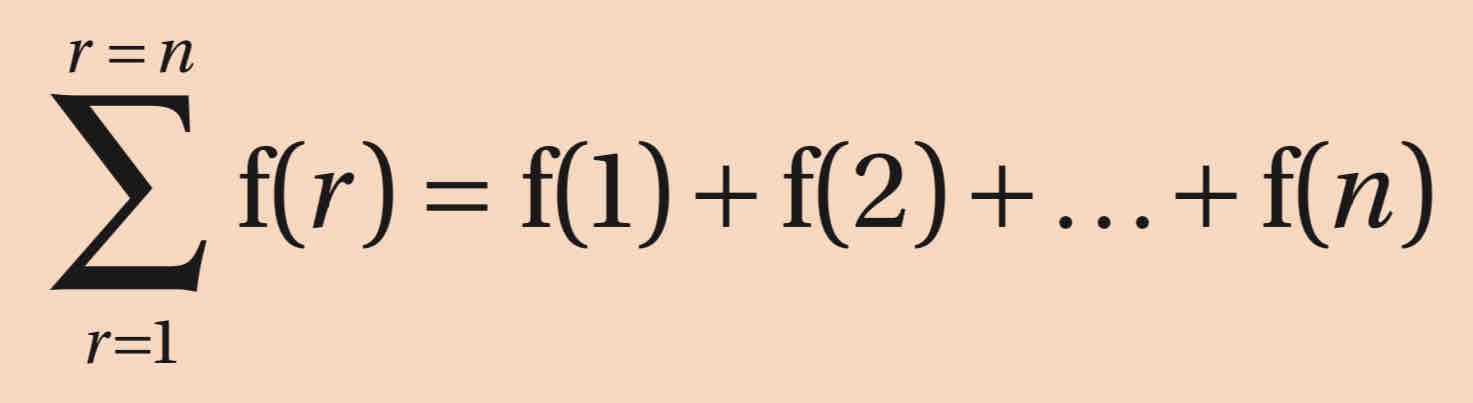
what does r=1 mean in sigma notation

where counting starts

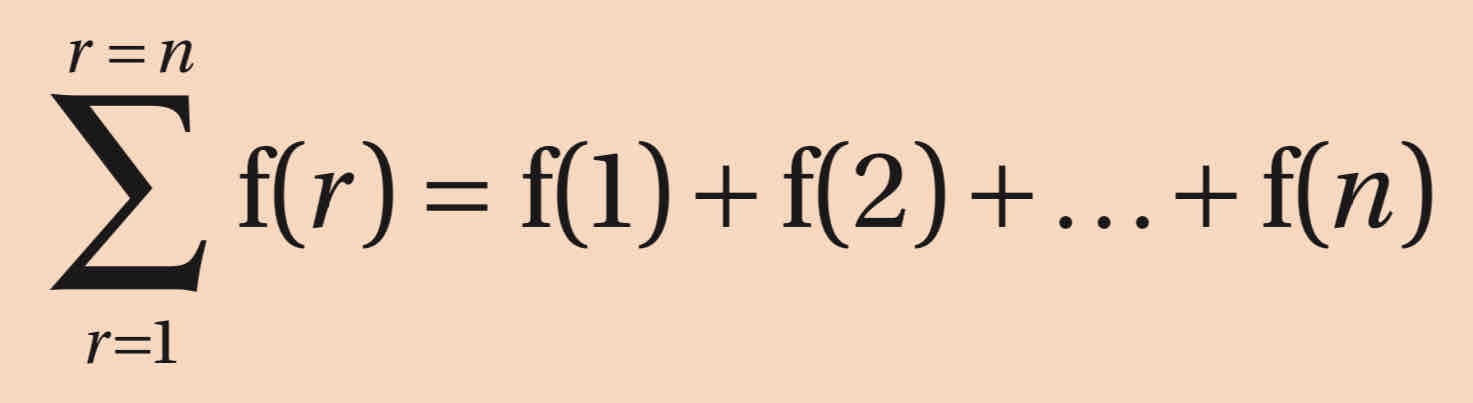
what does r=n mean in sigma notation

where counting ends

how to find nth term of an arithmetic sequence with first term a and common difference d

U_n= a+(n-1)d

what is the nth term of a geometric sequence with first term a and common ratio r

u = ar^n-1

what to do is common ratio isn’t obvious

divide second term by first term

in geometric sequences when asked which term satisfies a particular condition what would you use to help solve

logs 🥹

if r>1 then S n of the first n term is

S_n= a(r^n-1) / r-1

if |r|<1 what happens to series and the sum to infinity is what

• series converges

• S_n = a/1-r

when dealing with a mixed arithmetic and geometric questions what three things must you do

1. identify if it is arithmetic or geometric

2. is it asking for term or sum of?

3. form the equation

what is a rational function

both denominator and numerator are polynomials

what is the remainder term

• when simplifying rational functions, turn it into the sun of a polynomial and a simpler rational function

• p(x)/ax+b ≡ q(x) + r/ax+b

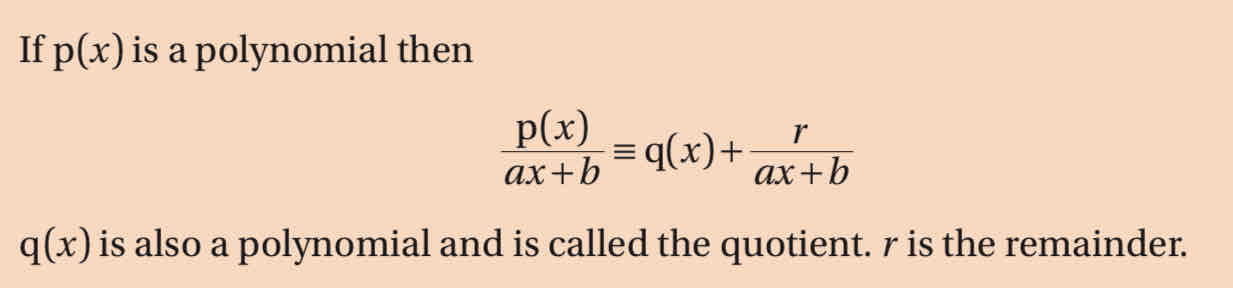
px + q/(ax+b)(cx+d)(ex+f) decomposes into what (partial fractions)

A/ax+b + B/cx+d + C/ex+f

px+q/(ax+b)(cx+d)² decomposes into (partial fractions but one denominators is squared)

A/ax+b + B/cx+d + C/(cx+d)²

360° is how many radians

2π radians

hwo to convert from degrees to radians

• divide by 180

• multiply by π

how to convert from radians to degrees

• divide by π

• multiply by 180

30° in radians is

π /6

45° in radians is

π /4

60° in radians is

π /3

90° in radians is

π /2

180° in radians is

π

what are some turning points of y=sinx

(π/2,1) (3π/2,-1)

when does y=sinx cross x axis

π and 2π so on

when are turning points of y=cosx

(0,1) (π/,-1) (2π,1)

when does y=cosx cross x axis

π/2 3π/2 and so on

what are the asymptotes of y=tanx

π/2 3π/2

what is arcsinx

the inverse function if sinx

what is the domain and range of arcsinx

domain [-1,1] and range is [-π/2,π/2]

what is the domain and range of arccosx

domain [-1,1] and range is [0,π]

what is the domain and range of arctanx

domain ℝ and range is (-π/2,π/2)

functions y=asinbx and y=acosbx have amplitude what and period what

amplitude a and period 2π/b

how to work out length of an arc in radians

l=rθ

what is the area of a sector in radians

A=1/2 r²θ

why is sinx=x (y=sinx and y=x)

because the two graphs are very close to each other at the origin

what is the double angle identity for sin2A≡

sin2A≡2sinA cosA

what are the double angle identities for cos2A≡

• cos² A-sin² A

• 2cos² A-1

• 1-2sin² A

what is the double angle identity for tan2A≡

≡ 2tanA/1-tan² A

how to write a sinx±b cosx in form Rsin(x±α) or Rcos(x±α)

• expand using compound angle identity

• equate coefficients to get equ for Rsinα and Rcosα

• to get R use R² = a² + b²

• to get α use tan α = sin α/cos α

what is the domain and range of y=secx

domain x∈ℝ range y≤ -1 y≥1 or (-∞,-1] ∪ [1,∞)

what is the domain and range of y=cosecx

domain x∈ℝ range y≤1 y≥1 or (-∞,-1]∪[1,∞)

what is the domain and range of y=cotx

domain x∈ℝ range ℝ

what can you rewrite secx as

≡ 1/cosx

what can you rewrite cosecx as

≡ 1/sinx

what can you rewrite cotx as

≡ 1/tanx

what can you rewrite cosec² x as

≡ 1 + cot² x

what can you rewrite sec² x as

≡ 1 + tan² x

change of base formula

log_b(x) = log_a(x) / log_a(b)

b = original base of logarithm

x = number you’re taking the log of

a = the new base you want to change to (a ≠ 1)

what is the derivative of e^x

dy/dx = e^x

what is the derivative of ln x

dy/dx = 1/x

what is the derivative of sin x

dy/dx = cos x

what is the derivative of cos x

dy/dx = - sin x

what is the derivative of tan x

dy/dx = sec² x

∫ e^x dx

e^x + c

∫ 1/x dx

ln |x| + c

∫ sin x dx

-cos x + c

∫ cos x dx

sin x + c

chain rule is

dy/dx = dy/du x du/dx

when would you use chain rule

y = f(u) where u = g(x)

product rule is

dy/dx = u’v + uv’

when to use product rule

y = u(x)v(x)

quotient rule is

dy/dx = u’v - uv’ / v²

what is the derivative of a^x

a^x ln a

what is derivative of the inverse function

dy/dx = 1 / (dy/dx)

when the top of the fraction is the derivative of the bottom

f’(x)/f(x) dx = ln |f(x)| + c

∫ sin² x dx use cos 2x ≡ 1 - 2 sin² x

sin² x ≡ ½ (1- cos 2x)

∫ cos² x dx use cos 2x ≡ 2 cos² x - 1

cos² x ≡ ½ (1 = cos 2x)

∫ √ a² - x² dx use the substitution x = ?

x = a sin θ

properties of convex curve :)

• curves upwards

• d²y/dx² > 0

properties of a concave curve :(

• curves downwards

• d²y/dx² < 0

for point of inflection

d²y/dx² = 0

how to find gradient of a parametric curve

chain rule dy/dx = dy/dt x dt/dx

area under the curve (x(t), y(t)) between points x=a and x=b given by

∫t₁^t₂ y dx/dt dt

the area bounded by two curves with equations y = f(x) and y = g(x), where curve g(x) is below curve f(x), is given by

A = ∫_a^b (f(x) - g(x)) dx

how to find area of curve and the y - axis

treat x as a function of y (reflection in the line y = x)

∫_c^d g(y) dy (x= g(y))

how to solve differential equation that can be written in the form dy/dx = f(x)g(x)

• get all xs one side all ys on the other side

• separate dy/dx as if it were a fraction

• integrate both sides

if dy/dx = f(y) then x = ?

x = ∫ 1/f(y) dy

the sign-change rule

if f(x) is a continuous function and a and b are numbers such that f(x) changes sign between a and a, then the equation f(x) = 0 has a root between a and b