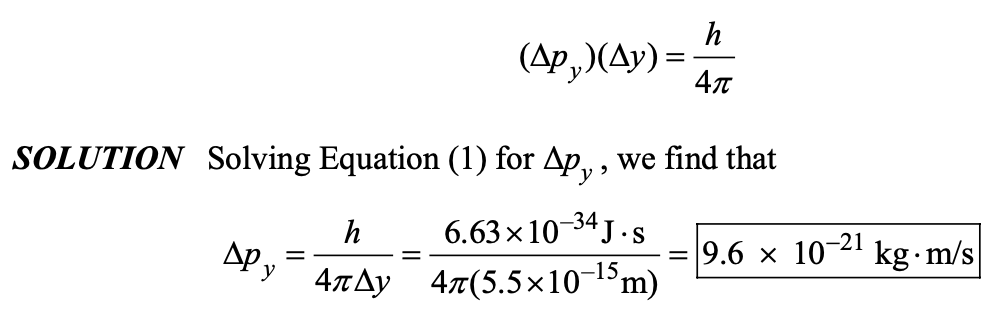Ch. 29 - Particles & Waves

Continuum - Black body radiation

Radiation emitted by a heated object

Examples of heated objects that emit radiation:

Light bulbs

Hot coals

Ice cubes

Starlight and sunlight can be…

Approximated as a black body radiation

Emission spectra is measured using:

A spectroscope

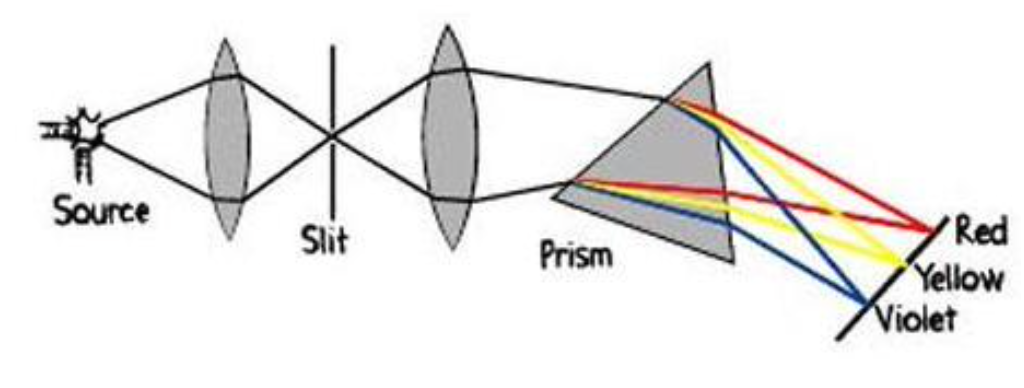
Emission spectra

The characteristic pattern of light frequencies emitted by elements is determined by their electron energy levels

Gasses and vapors in emission spectra

Discrete spectrum (single lines on a black background)

Every element has its own characteristic pattern of electron energy levels and therefore…

Emits light with its own characteristic pattern of frequencies, emission spectrum, when excited.

Absorption spectra

Dark lines agianst a rainbow-colored background.

Absorption is opposite of emission

Electrons absorb specific wavelengths to raise up to a higher energy level

Examples of absorption spectra

Stellar atmospheres

Cool interstellar clouds

Hydrogen series

Emission spectra of hydrogen

Equation determined by Johann Balmer (1855)

Line spectrum equations

Lyman series

Balmer series

Paschen series

Modern physics =

Quantum physics

Blackbody radiation

An object that absorbs all incident radiation, then reemits it according to its temperature (ex. the sun). A

All bodies, no matter how hot or cold,…

Continuously radiate electomagnetic waves.

Is light a wave or colored particles?

Three theories:

• Corpuscular theory of light

• Wave theory of light

• Absorption and emission of light

Corpuscular theory of light

Aristotle and Newton

Wave theory of light

Huygens and Maxwell

Absorption and emission of light

Plank and Einstein - Fathers of quantum theory

Einstein’s nobel prize

Only certian wavelengths eject electrons - The Photo-electron Effect

LIGHT - comes in “packets” of energy, called quanta

Now known as PHOTONS

Photoelectric Effect

Light is capable of ejecting electrons from various metal surfaces

The photoelectric effect depends on…

The light frequency and intensity only above the cut-off frequency.

Photoelectric effect phenomenon

Experimental evidence that light consists of photons

When light shines on a metal…

A photon can give up its energy to an electron in that metal.

Work Function

The minimum energy required to remove the least strongly held electrons

Photon’s energy

E = hf

Work function equation

KE = hf - Wo

fo = Wo/h

The Photoelectric Effect for a Silver Surface Example

The work function for a silver surface is 4.73 eV. Find the minimum

frequency that light must have to eject electrons from the surface.

263 nm (UV)

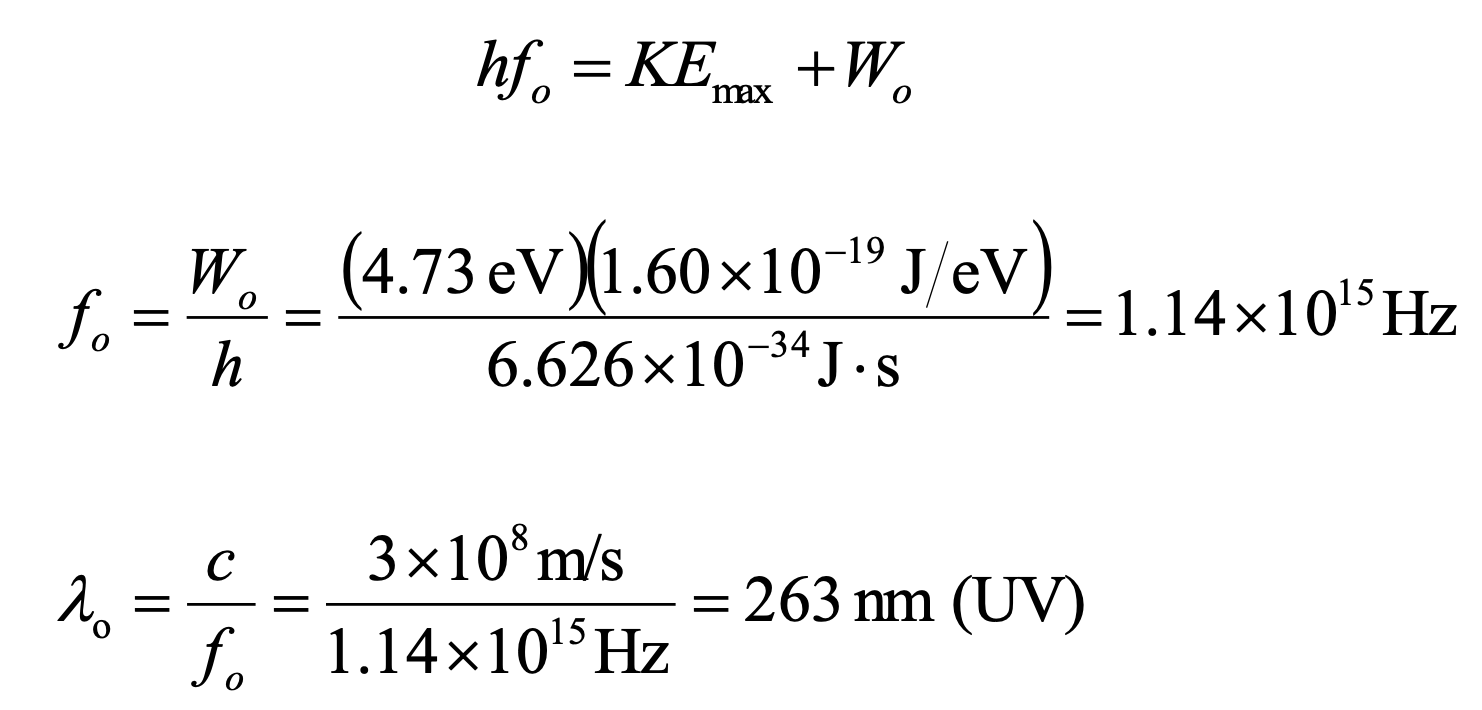
The Photoelectric Effect for a Silver Surface Example (Cont.)

UV radiation with a wavelength of 95 nm impinges on a silver surface

whose work function is 4.73 eV.

a) Will this light eject electrons from the surface?

b) What would be the speed of the ejected electrons?

a) Yes, the light will eject electrons from the surface

b) 1.72 × 10⁶ m/s

Compton Effect

The scattered photon and the recoil electron depart the collision in different directions. The scattered photon must have a smaller frequency.

Due to conservation of energy…

Scattered photon must have a smaller frequency (compton effect).

Incident X-ray photon’s energy =

Scattered photon’s energy + KE recoil electron

hf = hf’ + KE

Momentum of incident photon =

Momentum of scattered photon + momentum of recoil electron

Solar Sails and the Propulsion of Spaceships Example

One propulsion method that is currently being studied for interstellar

travel uses a large sail. The intent is that sunlight striking the sail

creates a force that pushes the ship away from the sun, much as wind

propels a sailboat. Does such a design have any hope of working and,

if so, should the surface facing the sun be shiny like a mirror or black,

in order to produce the greatest force?

Yes, it can work.

For best results the surface facing the sun should be shiny like a mirror.

Photons

All electromagnetic radiation consistes of particle-like entities called…

Photons have:

Energy and Momentum

Energy equation

E = hf

Momentum equation

p = h/λ

p = hf/c = E/c

Wave particle duality - Light

Light interferes with itself when viewed thorugh 2 slits

Wave particle duality - Electrons

2-slit experiment for electrons shows particle behavior

When a beam of electrons is used in a double slit experiment, a fringe pattern occurs, indicating interference effects.

Waves can exhibit…

Particle-like characteristics.

Particles can exhibit…

Wave-like characteristics.

de Broglie wavelength equation

λ = h/p

The de Broglie Wavelength of an Electron and a Baseball Example

Determine the de Broglie wavelength of (a) an electron moving at a speed

of 6.0x106 m/s and (b) a baseball (mass = 0.15 kg) moving at a speed

of 13 m/s.

a) 1.2 × 10^-10 m

b) 3.3 × 10^-34 m

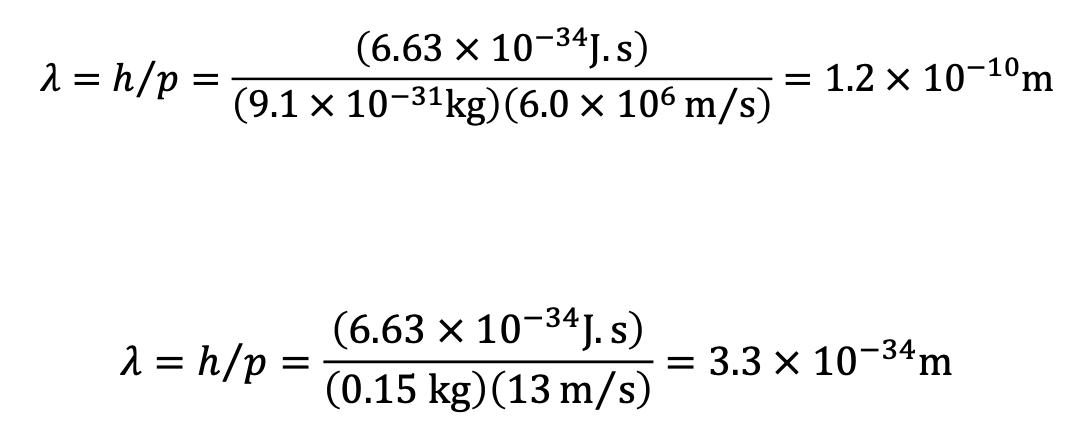
Example Question:

Two particles, A and B, have the same mass, but particle A has a

charge of +q and B has a charge of +2q. The particles are

accelerated from rest through the same potential difference. Which

one has the longer de Broglie wavelength at the end of the

acceleration?

(a) Particle A, because it has the greater momentum, and, hence,

the longer de Broglie wavelength.

(b) Particle B, because it has the greater momentum, and, hence,

the longer de Broglie wavelength.

(c) Particle A, because it has the smaller momentum, and, hence,

the longer de Broglie wavelength.

(d) Particle B, because it has the smaller momentum, and, hence,

the longer de Broglie wavelength.

(e) Both particles have the same de Broglie wavelength.

( c ) Particle A, because it has the smaller momentum, and, hence, the longer

de Broglie wavelength.

Neuron diffraction

A manifestation of the wave-like properties of particles

The Heisenberg uncertainty principle

We can know exactly posistion, but not momentum, or we can know mementum exactly, but not position.

Never both with accuracy.

Also true for time and energy.

Heisenberg uncertainty equation

(ΔE)(Δt) > or = h/4π

E = Uncertainty in the energy of a particle when the particle is in a certain state

t = time interval during which the particle is in that state

What if Planck’s Constant Were Large? Example

A bullet leaving the barrel of a gun is analogous to an electron passing

through the single slit. With this analogy in mind, what would hunting

be like if Planck’s constant has a relatively large value?

Hunting would be nearly impossible using conventional firearms. Bullets would behave like quantum particles, exhibiting unpredictable, wave-like behavior.

Heisenberg uncertainty principle Example

Suppose that the momentum of an electron is measured with complete accuracy (i.e., the uncertainty in its momentum is zero). The uncertainty in a simultaneous measurement of the electron’s position __________.

(a) is also zero

(b) is infinitely large

(c) is some finite value between zero and infinity

(d) cannot be measured, because one cannot measure the position and momentum of a particle, such as an electron, simultaneously.

(a) is also zero

Heisenberg Uncertainty Principle Example 2

A proton is confined to a nucleus that has a diameter of 5.5  10−15 m. If this distance is considered to be the uncertainty in the position of the proton, what is the minimum uncertainty in its momentum?

9.6 × 10^-21 kg . m/s